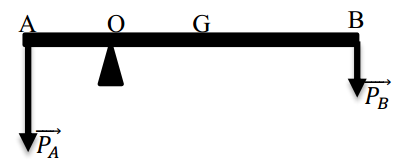
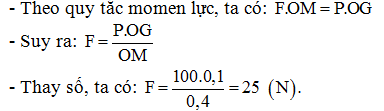50 bài tập Cân bằng của một vật có trục quay cố định

Câu hỏi 1 :

Điều kiện cân bằng của một vật chịu tác dụng của ba lực không song song là:

Ba lực đó phải có giá đồng phẳng, đồng quy và thoả mãn điều kiện

A
B
C
D

Đáp án: B

Lời giải chi tiết:

Đáp án - Lời giải

Câu hỏi 2 :

Để tăng mức vững vàng của trạng thái cân bằng đối với xe cần cẩu người ta chế tạo:

A Xe có khối lượng lớn.
B Xe có mặt chân đế rộng.
C Xe có mặt chân đế rộng và trọng tâm thấp.
D Xe có mặt chân đế rộng, và khối lượng lớn.

Đáp án: C

Lời giải chi tiết:

Để tăng mức vững vàng của trạng thái cân bằng đối với xe cần cẩu người ta chế tạo xe có mặt chân đế rộng và trọng tâm thấp.

Đáp án - Lời giải

Câu hỏi 3 :

Mômen lực của một lực đối với trục quay là bao nhiêu nếu độ lớn của lực là 5,5N và cánh tay đòn là 2 m?

A 10 N.
B 10 N.m
C 11N
D 11N.m

Đáp án: D

Phương pháp giải:

Áp dụng công thức: M = F.d

Lời giải chi tiết:

Áp dụng công thức:

$M = F.d = 5,5.2 = 11{\rm{ }}N.m$

Chọn D

Đáp án - Lời giải

Câu hỏi 4 :

Chọn đáp án đúng.

Ôtô chở hàng nhiều, chất đầy hàng nặng trên nóc xe dễ bị lật vì:

A Vị trí của trọng tâm của xe cao so với mặt chân đế.
B Giá của trọng lực tác dụng lên xe đi qua mặt chân đế.
C Mặt chân đế của xe quá nhỏ.
D Xe chở quá nặng.

Đáp án: A

Lời giải chi tiết:

Ôtô chở hàng nhiều, chất đầy hàng nặng trên nóc xe dễ bị lật vì vị trí của trọng tâm của xe cao so với mặt chân đế.

Đáp án - Lời giải

Câu hỏi 5 :

Điền từ cho sẵn dưới đây vào chỗ trống.“Muốn cho một vật có trục quay cố định ở trạng thái cân bằng, thì tổng .............. có xu hướng làm vật quay theo chiều kim đồng hồ phải bằng tổng các ..............có xu hướng làm vật quay ngược chiều kim đồng hồ.

A mômen lực.
B hợp lực.
C trọng lực.
D phản lực.

Đáp án: A

Phương pháp giải:

Điều kiện cân bằng của vật rắn có trục quay cố định.

Lời giải chi tiết:

Muốn cho một vật có trục quay cố định ở trạng thái cân bằng, thì tổng mômen có xu hướng làm vật quay theo chiều kim đồng hồ phải bằng tổng các mômen có xu hướng làm vật quay ngược chiều kim đồng hồ.

Đáp án - Lời giải

Câu hỏi 6 :

Tại sao không lật đổ được con lật đật?

A Vì nó được chế tạo ở trạng thái cân bằng bền.
B Vì nó được chế tạo ở trạng thái cân bằng không bền.
C Vì nó được chế tạo ở trạng thái cần bằng phiếm định.
D Vì nó có dạng hình tròn.

Đáp án: A

Lời giải chi tiết:

không lật đổ được con lật đật vì nó được chế tạo ở trạng thái cân bằng bền.

Đáp án - Lời giải

Câu hỏi 7 :

Đoạn thẳng nào sau đây là cánh tay đòn của lực?

A Khoảng cách từ vật đến giá của lực.
B Khoảng cách từ trục quay đến vật.
C Khoảng cách từ trục quay đến giá của lực.
D Khoảng cách từ trục quay đến điểm đặt của lực.

Đáp án: C

Lời giải chi tiết:

Khoảng cách từ trục quay đến giá của lực.

Đáp án - Lời giải

Câu hỏi 8 :

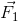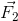Hai lực $\vec{F_{1}}$ và $\vec{F_{2}}$ song song cùng chiều, cách nhau đoạn 30cm. Một lực có F₁ = 18N, hợp lực F = 24N. Điểm đặt của hợp lực cách điểm đặt của lực F₂ đoạn là bao nhiêu?

Lời giải chi tiết:

Hai lực // cùng chiều nên: F = F₁ + F₂ = 24 F₂ = 6N

F₁.d₁ = F₂.d₂

18(d – d₂ ) = 6d₂ 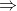$\Rightarrow$ d₂ = 22,5cm

Đáp án - Lời giải

Câu hỏi 9 :

Một người gánh 2 thúng, thúng gạo nặng 300N, thúng ngô nặng 200N. Đòn gánh dài 1,5m. Hỏi vai người ấy phải đặt ở điểm nào để đòn gánh cân bằng và vai chịu một lực là bao nhiêu? Bỏ qua trọng lượng của đòn gánh.

Lời giải chi tiết:

Gọi d₁ là khoảng cách từ thúng gạo đến vai, với lực P₁

d₂ là khoảng cách từ thúng ngô đến vai, với lực P₂

P₁.d₁ = P₂.d₂ 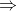$\Rightarrow$ 300d₁ = ( 1,5 – d₁).200

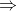$\Rightarrow$ d₁ = 0,6m d₂ = 0,9m

F = P₁ + P₂ = 500N

Đáp án - Lời giải

Câu hỏi 10 :

Một tấm ván nặng 240N được bắc qua con mương. Trọng tâm của tấm ván cách điểm tựa A 2,4m, cách B 1,2m. Xác định lực mà tấm ván tác dụng lên 2 bờ mương.

Lời giải chi tiết:

P = P₁ + P₂ = 240N P₁ = 240 – P₂

P₁.d₁ = P₂.d₂ ( 240 – P₂).2,4 = 1,2P₂

P₂ = 160N P₁ = 80N

Đáp án - Lời giải

Câu hỏi 11 :

Một người dùng chiếc búa dài 25cm để nhổ một cây đinh đóng ở một tấm gỗ. Biết lực tác dụng vào cây búa 180N là có thể nhổ được cây định. Hãy tìm lực tác dụng lên cây đinh để nó có thể bị nhổ ra khỏi tấm gỗ, d₂ = 9cm.

Lời giải chi tiết:

F₁.d₁ = F₂.d₂ 180.0,25 = F₂. 0,09

F₂ = 500N

Đáp án - Lời giải

Câu hỏi 12 :

Một người đang quẩy trên vai một chiếc bị có trọng lượng 50N. Chiếc bị buộc ở đầu gậy cách vai 60cm. Tay người giữ ở đầu kia cách vai 30cm. Bỏ qua trọng lượng của gậy.

Tính lực giữ của tay. Nếu dịch chuyển gậy cho bị cách vai 30cm và tay cách vai 60cm thì lực giữ là ?. Trong 2 trường hợp trên, vai người chịu một áp lực?

Lời giải chi tiết:

1. P₁ là trọng lượng bị, d₁ là khoảng cách từ vai đến bị.

F₂ là lực của tay, d₁ là khoảng cách từ vai đến tay

P₁.d₁ = F₂.d₂

50.0,6 = F₂. 0,3

F₂ = 100N

2. P₁.d^’₁ = F^’₂.d^’₂

50.0,3 = F₂. 0,6

F^’₂ = 25N

3. TH 1: P = P₁ + F₂ = 150N

TH 2: P = P₁ + F’₂ = 75N

Đáp án - Lời giải

Câu hỏi 13 :

Một người khiêng một vật vật nặng 1000N bằng một đòn dài 2m, người thứ nhất đặt điểm treo của vật cách vai mình 120cm. Bỏ qua trọng lượng của đòn gánh. Hỏi mỗi người chịu một lực là ?

Phương pháp giải:

Điều kiện cân bằng của vật rắn

Lời giải chi tiết:

Gọi d₁ là khoảng cách từ vật đến vai người 1 => d₁ = 1,2m

Gọi d₂ là khoảng cách từ vật đến vai người 2 => d₂ = 2 - 1,2 = 0,8m

P₁.d₁ = P₂.d₂

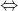$\Leftrightarrow$ P₁. 1,2 = 0,8.(1000 – P₁ )

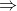$\Rightarrow$ P₁ = 400N 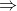$\Rightarrow$ P₂ = 600N

Đáp án - Lời giải

Câu hỏi 14 :

Hai người khiêng một vật nặng 1200N bằng một đòn tre dài 1m, một người đặt điểm treo của vật cách vai mình 40cm. Bỏ qua trọng lượng của đòn tre. Mỗi người phải chịu một lực bao nhiêu?

Lời giải chi tiết:

Gọi d₁ là khoảng cách từ điểm treo đến vai d₁ = 40cm

P = P₁ + P₂ = 1200 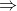$\Rightarrow$ P₁ = P – P₂ = 1200 – P₂

P₁.d₁ = P₂.d₂

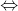$\Leftrightarrow$ (1200 – P₂ ).0,4 = P₂. 0,6

$\Rightarrow$ P₂ = 480N $\Rightarrow$ P₁ = 720N

Đáp án - Lời giải

Câu hỏi 15 :

Thước AB= 100cm, trọng lượng P = 10N, trọng tâm ở giữa thước. Thước có thể quay dễ dàng xung quanh một trục nằm ngang đi qua O với OA = 30cm. Để thước cân bằng và nằm ngang, ta cần treo một vật tại đầu A có trọng lượng bằng bao nhiêu?

Lời giải chi tiết:

Gọi l₁ là khoảng cách từ A đến O, l₂ là khoảng cách từ B đến O.

Ta có: l_1.P₂ = l₂.P₁

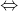$\Leftrightarrow$ 3P₂ = 7 P₁ (1)

Mặt khác: P = P₁ + P₂ (2)

Từ (1) và (2) 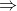$\Rightarrow$ P₁ = 0,3P ; P₂ = 0,7P

Gọi P^’ là trọng lượng của vật cần treo vào đầu A

Thanh cân bằng nằm ngang khi:

M_{P1(O )} + M_P(O) = M_P2(O)

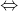$\Leftrightarrow$ P₁.15 + P^’.30 = P₂. 35

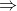$\Rightarrow$ P^’ = 6,67N

Đáp án - Lời giải

Câu hỏi 16 :

Một thanh AB dài 2m đồng chất có tiết diện đều, m = 2kg. Người ta treo vào đầu A của thanh một vật m = 5kg, đầu B một vật 1kg. Hỏi phải đặt một giá đỡ tại điểm O cách đầu A một khoảng OA là bao nhiêu để thanh cân bằng?

Lời giải chi tiết:

Áp dụng quy tắc momen lực: M_A = M_P + M_B

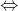$\Leftrightarrow$ P_A. OA = P. OI + P_B. OB

AI = IB = 1m

OI = AI – OA = 1 – OA

OB = OI – IB = 2 – OA

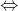$\Leftrightarrow$ 50. OA = 20 (1- OA) + 10( 2 – OA )

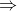$\Rightarrow$ OA = 0,5m

Đáp án - Lời giải

Câu hỏi 17 :

Momen lực đối với một trục quay là gì? Công thức, đơn vị của momen lực.

Lời giải chi tiết:

- Momen lực đối với một trục quay là là đại lượng đặc trưng cho tác dụng làm quay của lực và được đo bằng tích của lực với cánh tay đòn của nó.

- Công thức: M = F.d

- Đơn vị của momen lực là Niu-tơn mét (N.m).

Đáp án - Lời giải

Câu hỏi 18 :

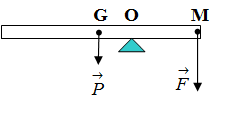
Một thanh kim loại đồng chất và tiết diện đều có trọng lượng P = 100 N có thể quay dễ dàng xung quanh một trục nằm ngang qua O với OG =10 cm. Tại đầu M cách O một khoảng40 cm, người ta kéo một lực có hướng như hình vẽ thì ta thấy thanh cân bằng. Hãy tính độ lớn của lực

Lời giải chi tiết:

Đáp án - Lời giải

Câu hỏi 19 :

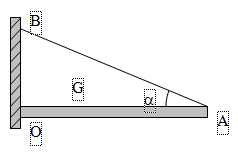
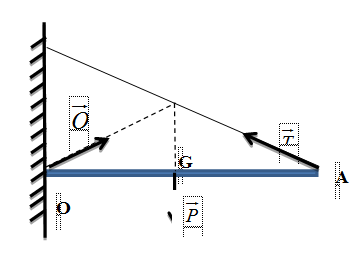
Một thanh dài AO, đều đồng chất, có khối lượng 1,0 kg. Một đầu O của thanh liên kết với tường bằng một bản lề, còn đầu A được treo vào tường bằng một sợi dây AB. Thanh được giữ nằm ngang và dây làm với thanh một góc a = 30^o(như hình vẽ). Lấy g = 10 m/s². Tính lực căng của dây.

Phương pháp giải:

Áp dụng điều kiện cân bằng của vật rắn có trục quay cố định

Lời giải chi tiết:

Các lực tác dụng lên OA gồm

$\overrightarrow P ,\overrightarrow T ,\overrightarrow Q $

OA đều, đồng chất nên G là trung điểm của OA. Xét trục quay tại O, ta có:

${M_Q} = 0$
${M_P} = {M_T}$

(OA cân bằng)

$ \Leftrightarrow P.OG.\sin {90^0} = T.OA.\sin \alpha ;{\rm{ }}\left( {OA = 2OG} \right)$

$\Leftrightarrow T = \frac{P}{{2\sin \alpha }} = \frac{{1.10}}{{2.\sin {{30}^0}}} = 10\,(N)$

Đáp án - Lời giải

Câu hỏi 20 :

Một người gánh một thùng gạo nặng 300N và một thùng ngô nặng 200N bằng một đòn gánh dài 1m. Bỏ qua trọng lượng của đòn gánh. Để đòn gánh nằm cân bằng trên vai thì người đó phải điều chỉnh vai đặt vào đòn gánh ở vị trí nào?

A
Cách đầu gánh gạo 0,6m.
B
Cách đầu gánh ngô 0,5m.
C Cách đầu gánh ngô 0,4m.
D Cách đầu gánh gạo 0,4m.

Đáp án: D

Phương pháp giải:

Áp dụng công thức momen lực

Lời giải chi tiết:

Coi vị trí đặt vai của đòn gánh là trục quay. Áp dụng quy tắc momen ta có

$\left\{ \begin{array}{l}
{d_g} + {d_n} = 1m\\
300.{d_g} = 200.{d_n}
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
{d_g} = 0,4m\\
{d_n} = 0,6m
\end{array} \right.$

Vậy gánh gạo cách vị trí vai 0,4 m.

Đáp án - Lời giải

Câu hỏi 21 :

Một thanh nhẹ nằm ngang, dài 7,0m có trục quay tại điểm cách đầu bên trái 2,0m. Một lực 50N hướng xuống tác dụng vào đầu bên trái và một lực 150N hướng xuống tác dụng vào đầu bên phải của thanh. Cần đặt lực 250N hướng lên tại điểm cách trục quay bao nhiêu để thanh cân bằng?

A
5,0m.
B 3,4m.
C 4,5m.
D 2,6m.

Đáp án: D

Phương pháp giải:

Áp dụng quy tắc momen lực

Lời giải chi tiết:

Áp dụng quy tắc momen lực ta có:

$\begin{array}{l}
{M_{t1}} + {M_{t2}} = {M_{p1}}\\
\Leftrightarrow 50.2 + {M_{t2}} = 150.5\\
= > {M_{t2}} = 150.5 - 50.2 = 650\\
\Leftrightarrow 250.d = 650 = > d = 2,6m
\end{array}$

Đáp án - Lời giải

Câu hỏi 22 :

Cho hệ cơ học như hình vẽ, thanh AB có thể quay được
quanh trục O. Cho g= 10m/s² AB = 80cm, AO = 20cm,
đầu A người ta treo một vật có khối lượng 15kg. Tính
khối lượng cần treo vào đầu B để thanh AB cân bằng
trong hai trường hợp:
a. Thanh nhẹ có khối lượng không đáng kể
b. Thanh đồng chất tiết diện đều có khối lượng 1,5kg.

A a. m = 5kg

b. m = 6kg
B a. m = 4kg

b. m = 5kg
C a. m = 5kg

b. m = 4kg
D a. m = 6kg

b. m = 5kg

Đáp án: C

Phương pháp giải:

Áp dụng quy tắc momen lực: Để thanh cân bằng thì tổng các momen do các lực làm nó quay theo chiều này phải bằng tổng các momen do các lực làm nó quay theo chiều ngược lại. Momen có công thức M = F.d với d là khoảng cách từ giá của lực đến trục quay

Lời giải chi tiết:

a) Thanh không có trọng lượng nên nó chỉ chịu tác dụng của hai lực P_A và P_B

P_A làm cho vật quay ngược chiều kim đồng hồ, P_B làm cho vật quay theo chiều kim đồng hồ. Trục quay tại O.

Áp dụng điều kiện cân bằng của vật rắn có trục quay cố định

$\begin{array}{l}
{M_A} = {M_B} \Leftrightarrow {P_A}.OA = {P_B}.OB\\
\Leftrightarrow {P_B} = \frac{{{P_A}.OA}}{{OB}} = \frac{{{m_A}.g.OA}}{{AB - OA}} = \frac{{15.10.20}}{{80 - 20}} = 50N\\
\Rightarrow {m_B} = \frac{{{P_B}}}{g} = \frac{{50}}{{10}} = 5kg
\end{array}$

Vậy cần treo vào B một vật có khối lượng 5 kg

b) Vì thanh có khối lượng 1,5 kg và đồng chất, tiết diện đều nên có trọng lực tác dụng lên thanh P_T tại vị trí trọng tâm G của thanh, nằm ở trung điểm của thanh.

P_A làm cho vật quay ngược chiều kim đồng hồ, P_T,P_B làm cho vật quay theo chiều kim đồng hồ. Trục quay tại O.

Áp dụng điều kiện cân bằng của vật rắn có trục quay cố định

$\begin{array}{l}
{M_A} = {M_T} + {M_B} \Leftrightarrow {P_A}.OA = {P_T}.OG + {P_B}.OB\\
\Leftrightarrow {P_B} = \frac{{{P_A}.OA - {P_T}.OG}}{{OB}} = \frac{{{m_A}.g.OA - {m_T}.g.\frac{{AB}}{2}}}{{AB - OA}} = \frac{{15.10.20 - 1,5.10.\frac{{80}}{2}}}{{80 - 20}} = 40N\\
\Rightarrow {m_B} = \frac{{{P_B}}}{g} = \frac{{40}}{{10}} = 4kg
\end{array}$

Vậy lúc này cần treo vào B vật có khối lượng 4 kg.

Đáp án - Lời giải

Câu hỏi 23 :

Trong trò chơi bập bênh giữa hai người có khối lượng tương ứng là : m₁ = 20 kg và m₂ = 15 kg trục quay O ở giữa ván ( ván đồng chất, tiết diện đều ). Người thứ I cách trục quay 1,2 m . Hỏi người thứ II phải cách trục quay bao xa để tấm ván cân bằng ?

A 1,2m
B 1,4m
C 1,6m
D 2m

Đáp án: C

Phương pháp giải:

- Trọng lượng của vật khối lượng m : P = mg

- Công thức tính mô men lực : M = F.d

- Điều kiện cân bằng của ván : Môn men lực của người thứ nhất cân bằng với mô men lực của người thứ hai.

Lời giải chi tiết:

Gọi d₁, d₂ là khoảng cách từ hai người đến trục quay

Để tấm ván cân bằng thì : M_F1 = M_F2

Hay : ${F_1}.{d_1} = {F_2}{d_2} \Rightarrow {P_1}.{d_1} = {P_2}{d_2} \Rightarrow {m_1}g.1,2 = {m_2}g.{d_2} \Rightarrow 20.1,2 = 15.{d_2} \Rightarrow {d_2} = 1,6m$

Đáp án - Lời giải

Câu hỏi 24 :

Một thanh đồng chất AB nhẹ, có chiều dài 0,6m. Khi đầu A gắn trục quay, đầu B được tác dụng một lực F vuông góc với mặt phẳng chứa trục quay và thanh AB, có độ lớn 25N. Tính mômen lực F đối với trục quay A?

A 20N.m
B 15N.m
C 30N.m
D 35N.m

Đáp án: B

Phương pháp giải:

Mô men lực đối với trục quay: M = F.d

Lời giải chi tiết:

Mô men của lực đối với trục quay A:

M = F.d = F.AB = 25.0,6 = 15 N.m

Đáp án - Lời giải

Câu hỏi 25 :

Một thanh AB đồng chất, tiết diện đều, có khối lượng không đáng kể, dài 1,2 m. Hai đầu A,B được treo các vật m₁có trọng lượng P₁ = 80N, vật m₂ có trọng lượng P₂ = 20N. Tại điểm C trên thanh AB, cách A 0,5m, treo thêm vật m₃ có trọng lượng P₃ = 30N. Hãy xác định vị trí đặt trục quay O trên thanh AB, O cách A một đoạn bao nhiêu để thanh cân bằng nằm ngang?

A 0,1m
B 0,2m
C 0,3m
D 0,4m

Đáp án: C

Phương pháp giải:

Điều kiện cân bằng: Tổng Mô men của những lực làm vật quay cùng chiều kim đồng hồ bằng tổng mô men của những lực làm vật quay ngược chiều kim đồng hồ.

Mô men lực: M = F.d

Lời giải chi tiết:

Giả sử O nằm trong đoạn BC

Gọi d₁, d₂, d₃ lần lượt là khoảng cách từ giá của trọng lực các vật m₁, m₂, m₃đến O

Điều kiện cân bằng: M_P1 + M_P3 = M_P2

Hay: ${P_1}.{\rm{ }}OA + {P_3}.OC = {P_2}.OB \Leftrightarrow {P_1}.OA + {P_3}.\left( {OA - 0,5} \right) = {P_2}.\left( {1,2-OA} \right) \Rightarrow OA = 3m$

Vậy điểm O nằm giữa A và C, cách A một đoạn 0,3m

Đáp án - Lời giải

Câu hỏi 26 :

Đòn bẩy AB dài 50 cm nhẹ, cứng như hình vẽ

Đầu A của đòn bẩy treo một vật có trọng lượng 30N. Khoảng cách từ đầu A đến trục quay O là 20 cm. Muốn đòn bẩy AB cân bằng thì đầu B của đòn bẩy phải treo vật có trọng lượng là

A 15N.
B 30 N.
C 25 N.
D 20 N.

Đáp án: D

Phương pháp giải:

Áp dụng điều kiện cân bằng của vật rắn có trục quay cố định

Lời giải chi tiết:

Trọng lượng của vật cần treo vào đầu B có trọng lượng là P_B

Theo quy tắc momen ta có M₁ = M₂ ó P_A.d_A = P_B.d_B ó 30.20 = P_B.30

=> P_B = 20 N

Chọn đáp án D

Đáp án - Lời giải

Câu hỏi 27 :

Một lực có độ lớn 10N tác dụng lên một vật rắn quay quanh một trục cố định, biết khoảng cách từ giá của lực đến trục quay là 20cm. Mômen của lực tác dụng lên vật có giá trị là

A 200N. m
B 200N/m
C 2N.m
D 2N/m

Đáp án: C

Phương pháp giải:

Momen lực đối với một trục quay là đại lượng đặc trưng cho tác dụng làm quay của lực và được đo bằng tích của lực với cánh tay đòn của nó: $M = F.d$

Lời giải chi tiết:

Momen của lực tác dụng lên vật có giá trị là:

$M = F.d = 10.0,2 = 2N.m$

Chọn C.

Đáp án - Lời giải

Câu hỏi 28 :

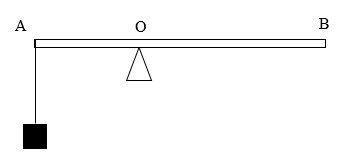
Một người gánh một thúng lúa và một thúng gạo, thúng lúa nặng 10kg, thúng gạo nặng 15kg. Đòn gánh dài 1,5m, hai thúng đặt ở hai đầu mút của đòn gánh. Xác định vị trí đòn gánh đặt trên vai để đòn gánh cân bằng nằm ngang.

A Vai đặt ở vị trí cách đầu gánh thúng lúa 0,6m và cách đầu gánh thúng gạo 0,9m.
B Vai đặt ở vị trí cách đầu gánh thúng lúa 1m và cách đầu gánh thúng gạo 0,5m.
C Vai đặt ở vị trí cách đầu gánh thúng lúa 0,9m và cách đầu gánh thúng gạo 0,6m.
D Vai đặt ở vị trí cách đầu gánh thúng lúa 0,5m và cách đầu gánh thúng gạo 1m.

Đáp án: C

Phương pháp giải:

+ Momen lực đối với một trục quay là đại lượng đặc trưng cho tác dụng làm quay của lực và được đo bằng tích của lực với cánh tay đòn của nó: $M = F.d$

+ Quy tắc monen lực: Muốn cho một vật có trục quay cố định ở trạng thái cân bằng, thì tổng các momen có xu hướng làm vật quay theo chiều kim đồng hồ phải bằng tổng các momen lực có xu hướng làm vật quay ngược chiều kim đồng hồ.

Lời giải chi tiết:

Hình vẽ biểu diễn các lực tác dụng vào vai người. Gọi O là điểm đặt của vai.

Trọng lượng của gạo và lúa là: $\left\{ \begin{array}{l}{P_1} = 150N\\{P_2} = 100N\end{array} \right.$

Ta có: ${d_1} + {d_2} = 1,5m\,\,\,\left( 1 \right)$

Để đòn gánh cân bằng nằm ngang thì:

${P_1}{d_1} = {P_2}{d_2} \Leftrightarrow 150.{d_1} = 100{d_2} \Leftrightarrow 150{d_1} - 100{d_2} = 0\,\,\,\left( 2 \right)$

Từ (1) và (2) $ \Rightarrow \left\{ \begin{array}{l}{d_1} = 0,6m\\{d_2} = 0,9m\end{array} \right.$

Vậy vai đặt ở vị trí cách đầu gánh thúng lúa 0,9m và cách đầu gánh thúng gạo 0,6m.

Chọn C.

Đáp án - Lời giải

Câu hỏi 29 :

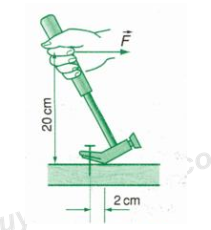
Một người dùng búa để nhổ một chiếc đinh. Khi người ấy tác dụng một lực F = 150N vào đầu búa thì đinh bắt đầu chuyển động. Lực cản của gỗ tác dụng vào đinh bằng

A 500N.
B 1000N.
C 1500N.
D 2000N.

Đáp án: C

Phương pháp giải:

+ Momen lực đối với một trục quay là đại lượng đặc trưng cho tác dụng làm quay của lực và được đo bằng tích của lực với cánh tay đòn của nó: $M = F.d$

+ Quy tắc monen lực: Muốn cho một vật có trục quay cố định ở trạng thái cân bằng, thì tổng các momen có xu hướng làm vật quay theo chiều kim đồng hồ phải bằng tổng các momen lực có xu hướng làm vật quay ngược chiều kim đồng hồ.

Lời giải chi tiết:

Gọi d_Flà cánh tay đòn của lực F, ta có: ${d_F}\; = 20cm = 0,2m$

Gọi d_C là cánh tay đòn của lực cản gỗ: ${d_{C\;}} = 2cm = 0,02m$

Áp dụng quy tắc Momen lực ta có:

$F.{d_F} = {F_C}.{d_C} \Rightarrow {F_C} = \dfrac{{F.{d_F}}}{{{d_C}}} = \dfrac{{150.0,2}}{{0,02}} = 1500N$

Chọn C.

Đáp án - Lời giải

Câu hỏi 30 :

Momen lực của một lực đối với trục quay là bao nhiêu nếu độ lớn của lực là 5,5N và cánh tay đòn là 2 mét?