40 bài tập vận dụng Rút gọn biểu thức chứa căn thức bậc hai
Làm đề thiCâu hỏi 1 :
![]()
- A x có 2 giá trị thỏa mãn
- B x có 3 giá trị thỏa mãn
- C x có 4 giá trị thỏa mãn
- D x có 5 giá trị thỏa mãn
Đáp án: B
Lời giải chi tiết:
Câu hỏi 6 :
Cho hai biểu thức \(A = \frac{{\sqrt x + 2}}{{\sqrt x - 5}}\) và \(B = \frac{3}{{\sqrt x + 5}} + \frac{{20 - 2\sqrt x }}{{x - 25}}\) ,với \(x \ge 0,x \ne 25\).
1. Tính giá trị biểu thức A khi \(x = 9\) 2. Chứng minh rằng \(B = \frac{1}{{\sqrt x - 5}}.\)
Phương pháp giải:
1. Thay \(x = 9\) vào biểu thức A.
2. Chứng minh hiệu \(B - \frac{1}{{\sqrt x - 5}} = 0\).
Lời giải chi tiết:
1. Với \(x = 9\) thỏa mãn điều kiện \(x \ge 0,x \ne 25\), ta có \(A = \frac{{\sqrt x + 2}}{{\sqrt x - 5}} = \frac{{\sqrt 9 + 2}}{{\sqrt 9 - 5}} = \frac{{3 + 2}}{{3 - 5}} = - \frac{5}{2}\)
Vậy \(A = - \frac{5}{2}\)
2. Xét hiệu \(B - \frac{1}{{\sqrt x - 5}}\), ta có
\(\begin{array}{l}\frac{3}{{\sqrt x + 5}} + \frac{{20 - 2\sqrt x }}{{x - 25}} - \frac{1}{{\sqrt x - 5}}\\ = \frac{3}{{\sqrt x + 5}} - \frac{1}{{\sqrt x - 5}} + \frac{{20 - 2\sqrt x }}{{x - 25}}\\ = \frac{{3\left( {\sqrt x - 5} \right) - \left( {\sqrt x + 5} \right)}}{{\left( {\sqrt x - 5} \right)\left( {\sqrt x + 5} \right)}} + \frac{{20 - 2\sqrt x }}{{\left( {\sqrt x - 5} \right)\left( {\sqrt x + 5} \right)}}\\ = - \frac{{20 - 2\sqrt x }}{{\left( {\sqrt x - 5} \right)\left( {\sqrt x + 5} \right)}} + \frac{{20 - 2\sqrt x }}{{\left( {\sqrt x - 5} \right)\left( {\sqrt x + 5} \right)}} = 0\end{array}\)
Vậy \(\frac{3}{{\sqrt x + 5}} + \frac{{20 - 2\sqrt x }}{{x - 25}}\)\( = \frac{1}{{\sqrt x - 5}}\)hay B\( = \frac{1}{{\sqrt x - 5}}\)
Câu hỏi 7 :
Cho biểu thức \(A = \frac{{x - 1}}{{\left( {x + \sqrt x } \right)\left( {x - \sqrt x + 1} \right)}}:\frac{1}{{{x^2} + \sqrt x }}\)
1. Rút gọn A 2. Tìm x sao cho \(A\left( {\sqrt x + 1} \right) > 0\)
- A 1,\(A = x - 1\).
2, \(x > 1.\)
- B 1,\(A = x - 1\).
2, \(x < 1.\)
- C 1,\(A = x - 2\).
2, \(x > 1.\)
- D 1,\(A = x - 3\).
2, \(x > 1.\)
Đáp án: A
Phương pháp giải:
1. Sử dụng hằng đẳng thức, phân tích thành nhân tử và rút gọn.
2. \(f\left( x \right).g\left( x \right) > 0 \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}f\left( x \right) > 0\\g\left( x \right) > 0\end{array} \right.\\\left\{ \begin{array}{l}f\left( x \right) < 0\\g\left( x \right) < 0\end{array} \right.\end{array} \right.\)
Lời giải chi tiết:
1. Rút gọn biểu thức A
ĐK \(x > 0\).
Ta có:
\(\begin{array}{l}A = \frac{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}{{\sqrt x \left( {\sqrt x + 1} \right)\left( {x - \sqrt x + 1} \right)}}:\frac{1}{{\sqrt x \left( {x\sqrt x + 1} \right)}}\\A = \frac{{\sqrt x - 1}}{{\sqrt x \left( {x - \sqrt x + 1} \right)}}.\sqrt x \left( {x\sqrt x + 1} \right)\\A = \frac{{\left( {\sqrt x - 1} \right)\left( {x\sqrt x + 1} \right)}}{{x - \sqrt x + 1}}\\A = \frac{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)\left( {x - \sqrt x + 1} \right)}}{{x - \sqrt x + 1}}\\A = \left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right) = x - 1\end{array}\)
Vậy \(A = x - 1\).
2. Ta có :
\(\begin{array}{l}A\left( {\sqrt x + 1} \right) > 0 \Leftrightarrow \left( {x - 1} \right)\left( {\sqrt x + 1} \right) > 0\\Do\,\,\sqrt x + 1 > 0 \Rightarrow x - 1 > 0 \Leftrightarrow x > 1\end{array}\)
Vậy \(x > 1.\)
Câu hỏi 8 :
Chọn đáp án đúng nhất:
Câu 1: Thực hiện phép tính: \(2\sqrt 9 - 3\sqrt 4 .\)
- A \(0\)
- B \(1\)
- C \(\sqrt 2 \)
- D \(\sqrt 3 \)
Đáp án: A
Phương pháp giải:
Sử dụng công thức: \(\sqrt {{A^2}B} = \left| A \right|\sqrt B = \left\{ \begin{array}{l}A\sqrt B \,\,\,khi\,\,\,A \ge 0\\ - A\sqrt B \,\,\,khi\,\,\,A < 0\end{array} \right..\)
Lời giải chi tiết:
Ta có: \(2\sqrt 9 - 3\sqrt 4 = 2\sqrt {{3^2}} - 3\sqrt {{2^2}} = 2.3 - 3.2 = 0.\)
Chọn A.
Câu 2: Rút gọn biểu thức: \(\sqrt {\frac{{28{{\left( {a - 2} \right)}^2}}}{7}} ,\) với \(a > 2.\)
- A \(4 - 2a\)
- B \(2a - 4\)
- C \(a - 2\)
- D \(2 - a\)
Đáp án: B
Phương pháp giải:
Sử dụng công thức: \(\sqrt {{A^2}B} = \left| A \right|\sqrt B = \left\{ \begin{array}{l}A\sqrt B \,\,\,khi\,\,\,A \ge 0\\ - A\sqrt B \,\,\,khi\,\,\,A < 0\end{array} \right..\)
Lời giải chi tiết:
\(\sqrt {\frac{{28{{\left( {a - 2} \right)}^2}}}{7}} = \sqrt {4{{\left( {a - 2} \right)}^2}} = \sqrt {{{\left[ {2\left( {a - 2} \right)} \right]}^2}} = \left| {2\left( {a - 2} \right)} \right| = 2\left( {a - 2} \right) = 2a - 4.\,\,\,\,\left( {do\,\,\,a > 2 \Rightarrow a - 2 > 0} \right).\)
Vậy với \(a > 2\) thì \(\sqrt {\frac{{28{{\left( {a - 2} \right)}^2}}}{7}} = 2a - 4.\)
Chọn B.
Câu 3: Tìm tọa độ các giao điểm của đồ thị hàm số \(y = {x^2}\) và đồ thị hàm số \(y = 3x - 2.\)
- A \(A\left( {2;\,\,4} \right),\,\,B\left( {1;\,\, - 1} \right).\)
- B \(A\left( { - 2;\,\,4} \right),\,\,B\left( { - 1;\,\,1} \right).\)
- C \(A\left( { - 2;\,\,4} \right),\,\,B\left( { - 1;\,\, - 1} \right).\)
- D \(A\left( {2;\,\,4} \right),\,\,B\left( {1;\,\,1} \right).\)
Đáp án: D
Phương pháp giải:
Giải phương trình hoành độ giao điểm của hai đồ thị hàm số để tìm hoành độ giao điểm rồi thế vào 1 trong 2 công thức hàm số để tìm tung độ giao điểm rồi kết luận.
Lời giải chi tiết:
Xét phương trình hoành độ giao điểm của hai đồ thị hàm số ta có:
\(\begin{array}{l}\,\,\,\,\,\,\,{x^2} = 3x - 2\\ \Leftrightarrow {x^2} - 3x + 2 = 0 \Leftrightarrow {x^2} - 2x - x - 2 = 0\\ \Leftrightarrow x\left( {x - 2} \right) - \left( {x - 2} \right) = 0 \Leftrightarrow \left( {x - 2} \right)\left( {x - 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 2 = 0\\x - 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 2 \Rightarrow y = {2^2} = 4 \Rightarrow A\left( {2;\,\,4} \right)\\x = 1 \Rightarrow y = {1^2} = 1 \Rightarrow B\left( {1;\,\,1} \right)\end{array} \right..\end{array}\)
Vậy hai đồ thị hàm số cắt nhau tại hai điểm phân biệt \(A\left( {2;\,\,4} \right),\,\,B\left( {1;\,\,1} \right).\)
Chọn D.
Câu hỏi 9 :
Rút gọn các biểu thức sau:
Câu 1: \(P = \left( {\frac{2}{{\sqrt x - 2}} + \frac{{\sqrt x - 1}}{{2\sqrt x - x}}} \right):\left( {\frac{{\sqrt x + 2}}{{\sqrt x }} - \frac{{\sqrt x - 1}}{{\sqrt x - 2}}} \right)\)
- A \(P= \frac{{\sqrt x + 1}}{{\sqrt x - 4}}\)
- B \(P= \frac{{\sqrt x - 1}}{{\sqrt x - 4}}\)
- C \(P= \frac{{\sqrt x + 1}}{{\sqrt x + 4}}\)
- D \(P= \frac{{\sqrt x - 1}}{{\sqrt x + 4}}\)
Đáp án: A
Lời giải chi tiết:
\(P = \left( {\frac{2}{{\sqrt x - 2}} + \frac{{\sqrt x - 1}}{{2\sqrt x - x}}} \right):\left( {\frac{{\sqrt x + 2}}{{\sqrt x }} - \frac{{\sqrt x - 1}}{{\sqrt x - 2}}} \right)\)
Điều kiện: \(x > 0;x \ne 4\)
\(\begin{array}{l}P = \left( {\frac{2}{{\sqrt x - 2}} + \frac{{\sqrt x - 1}}{{2\sqrt x - x}}} \right):\left( {\frac{{\sqrt x + 2}}{{\sqrt x }} - \frac{{\sqrt x - 1}}{{\sqrt x - 2}}} \right)\\\,\,\,\, = \left( {\frac{2}{{\sqrt x - 2}} - \frac{{\sqrt x - 1}}{{\sqrt x \left( {\sqrt x - 2} \right)}}} \right):\left( {\frac{{\sqrt x + 2}}{{\sqrt x }} - \frac{{\sqrt x - 1}}{{\sqrt x - 2}}} \right)\\\,\,\, = \frac{{\sqrt x + 1}}{{\sqrt x \left( {\sqrt x - 2} \right)}}:\frac{{x - 4 - x + \sqrt x }}{{\sqrt x \left( {\sqrt x - 2} \right)}}\\\,\,\, = \frac{{\sqrt x + 1}}{{\sqrt x \left( {\sqrt x - 2} \right)}}.\frac{{\sqrt x \left( {\sqrt x - 2} \right)}}{{\sqrt x - 4}}\\\,\, = \frac{{\sqrt x + 1}}{{\sqrt x - 4}}.\end{array}\)
Câu 2: \(Q = \left( {\frac{{x + 2}}{{\sqrt x + 1}} - \sqrt x } \right):\left( {\frac{{\sqrt x - 4}}{{1 - x}} - \frac{{\sqrt x }}{{\sqrt x + 1}}} \right)\)
- A \(Q= \frac{{\sqrt x + 1}}{{\sqrt x - 2}}\)
- B \(Q= \frac{{\sqrt x - 1}}{{\sqrt x - 2}}\)
- C \(Q= \frac{{\sqrt x + 1}}{{\sqrt x + 2}}\)
- D \(Q= \frac{{\sqrt x - 1}}{{\sqrt x + 2}}\)
Đáp án: D
Lời giải chi tiết:
\(Q = \left( {\frac{{x + 2}}{{\sqrt x + 1}} - \sqrt x } \right):\left( {\frac{{\sqrt x - 4}}{{1 - x}} - \frac{{\sqrt x }}{{\sqrt x + 1}}} \right)\)
Điều kiện: \(x \ge 0,\,\,x \ne 1,\,\,x \ne 4.\)
\(\begin{array}{l}Q = \left( {\frac{{x + 2}}{{\sqrt x + 1}} - \sqrt x } \right):\left( {\frac{{\sqrt x - 4}}{{1 - x}} - \frac{{\sqrt x }}{{\sqrt x + 1}}} \right)\\\,\,\,\,\, = \left( {\frac{{x + 2 - \sqrt x \left( {\sqrt x + 1} \right)}}{{\sqrt x + 1}}} \right):\left( {\frac{{4 - \sqrt x }}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}} - \frac{{\sqrt x }}{{\sqrt x + 1}}} \right)\\\,\,\,\, = \frac{{x + 2 - x - \sqrt x }}{{\sqrt x + 1}}:\frac{{4 - \sqrt x - \sqrt x \left( {\sqrt x - 1} \right)}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}}\\\,\,\,\, = \frac{{2 - \sqrt x }}{{\sqrt x + 1}}:\frac{{4 - \sqrt x - x + \sqrt x }}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}} = \frac{{2 - \sqrt x }}{{\sqrt x + 1}}:\frac{{4 - x}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}}\\\,\,\, = \frac{{2 - \sqrt x }}{{\sqrt x + 1}}.\frac{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}}{{\left( {2 - \sqrt x } \right)\left( {2 + \sqrt x } \right)}}\, = \frac{{\sqrt x - 1}}{{\sqrt x + 2}}.\end{array}\)
Câu 3: \(R = \left( {\frac{{3\sqrt x }}{{\sqrt x + 2}} + \frac{{\sqrt x }}{{\sqrt x - 2}} + \frac{{3x - 5\sqrt x }}{{4 - x}}} \right):\left( {\frac{{2\sqrt x - 1}}{{\sqrt x - 2}} - 1} \right)\)
- A \(R= -\frac{{\sqrt x }}{{\sqrt x - 2}}\)
- B \(R= \frac{{\sqrt x }}{{\sqrt x - 2}}\)
- C \(R= \frac{{\sqrt x }}{{\sqrt x + 2}}\)
- D \(R= -\frac{{\sqrt x }}{{\sqrt x + 2}}\)
Đáp án: C
Lời giải chi tiết:
\(R = \left( {\frac{{3\sqrt x }}{{\sqrt x + 2}} + \frac{{\sqrt x }}{{\sqrt x - 2}} + \frac{{3x - 5\sqrt x }}{{4 - x}}} \right):\left( {\frac{{2\sqrt x - 1}}{{\sqrt x - 2}} - 1} \right)\)
Điều kiện: \(x \ge 0,\,\,\,x \ne 4.\)
\(\begin{array}{l}R = \left( {\frac{{3\sqrt x }}{{\sqrt x + 2}} + \frac{{\sqrt x }}{{\sqrt x - 2}} + \frac{{3x - 5\sqrt x }}{{4 - x}}} \right):\left( {\frac{{2\sqrt x - 1}}{{\sqrt x - 2}} - 1} \right)\\\,\,\,\, = \left( {\frac{{3\sqrt x }}{{\sqrt x + 2}} + \frac{{\sqrt x }}{{\sqrt x - 2}} - \frac{{3x - 5\sqrt x }}{{(\sqrt x - 2)(\sqrt x + 2)}}} \right):\left( {\frac{{2\sqrt x - 1 - \sqrt x + 2}}{{\sqrt x - 2}}} \right)\\\,\,\,\, = \frac{{3\sqrt x \left( {\sqrt x - 2} \right) + \sqrt x \left( {\sqrt x + 2} \right) - 3x + 5\sqrt x }}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}:\frac{{\sqrt x + 1}}{{\sqrt x - 2}}\\\,\,\,\, = \frac{{3x - 6\sqrt x + x + 2\sqrt x - 3x + 5\sqrt x }}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}:\frac{{\sqrt x + 1}}{{\sqrt x - 2}}\\\,\,\, = \frac{{x + \sqrt x }}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}:\frac{{\sqrt x + 1}}{{\sqrt x - 2}}\\\,\,\, = \frac{{\sqrt x \left( {\sqrt x + 1} \right)}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}.\frac{{\sqrt x - 2}}{{\sqrt x + 1}}\\\,\,\, = \frac{{\sqrt x }}{{\sqrt x + 2}}.\end{array}\)
Câu 4: \(S = \left( {\frac{{\sqrt x + 3}}{{\sqrt x - 2}} + \frac{{\sqrt x + 2}}{{3 - \sqrt x }} + \frac{{\sqrt x + 2}}{{x - 5\sqrt x + 6}}} \right):\left( {1 - \frac{{\sqrt x }}{{\sqrt x + 1}}} \right)\)
- A \(S= \frac{{\sqrt x - 1}}{{\sqrt x - 2}}\)
- B \(S= \frac{{\sqrt x + 1}}{{\sqrt x - 2}}\)
- C \(S= \frac{{\sqrt x + 1}}{{\sqrt x + 2}}\)
- D \(S= \frac{{\sqrt x - 1}}{{\sqrt x + 2}}\)
Đáp án: B
Lời giải chi tiết:
\(\begin{array}{l}4)\,\,S = \left( {\frac{{\sqrt x + 3}}{{\sqrt x - 2}} + \frac{{\sqrt x + 2}}{{3 - \sqrt x }} + \frac{{\sqrt x + 2}}{{x - 5\sqrt x + 6}}} \right):\left( {1 - \frac{{\sqrt x }}{{\sqrt x + 1}}} \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\left( {DK:\,\,x \ge 0,\,\,x \ne 4,\,\,x \ne 9} \right)\\\,\,\,\,\,\,\,\,\,\,\, = \left( {\frac{{\sqrt x + 3}}{{\sqrt x - 2}} - \frac{{\sqrt x + 2}}{{\sqrt x - 3}} + \frac{{\sqrt x + 2}}{{(\sqrt x - 3).(\sqrt x - 2)}}} \right):\left( {\frac{{\sqrt x + 1 - \sqrt x }}{{\sqrt x + 1}}} \right)\\\,\,\,\,\,\,\,\,\,\, = \frac{{(\sqrt x + 3)(\sqrt x - 3) - (\sqrt x + 2)(\sqrt x - 2) + \sqrt x + 2}}{{(\sqrt x - 3).(\sqrt x - 2)}}:\frac{1}{{\sqrt x + 1}}\\\,\,\,\,\,\,\,\,\,\, = \frac{{x - 9 - (x - 4) + \sqrt x + 2}}{{(\sqrt x - 3).(\sqrt x - 2)}}:\frac{1}{{\sqrt x + 1}}\\\,\,\,\,\,\,\,\,\, = \frac{{x - 9 - x + 4 + \sqrt x + 2}}{{(\sqrt x - 3).(\sqrt x - 2)}}:\frac{1}{{\sqrt x + 1}}\\\,\,\,\,\,\,\,\, = \frac{{\sqrt x - 3}}{{(\sqrt x - 3).(\sqrt x - 2)}}.(\sqrt x + 1)\\\,\,\,\,\,\,\,\, = \frac{{\sqrt x + 1}}{{\sqrt x - 2}}.\end{array}\)
Câu 5: \(T = \frac{{\sqrt x + 1}}{{x - 1}} - \frac{{x + 2}}{{x\sqrt x - 1}} - \frac{{\sqrt x + 1}}{{x + \sqrt x + 1}}\)
- A \(T= \frac{{ - \sqrt x }}{{x + \sqrt x + 1}}\)
- B \(T= \frac{{ - \sqrt x }}{{x - \sqrt x + 1}}\)
- C \(T= \frac{{ \sqrt x }}{{x + \sqrt x + 1}}\)
- D \(T= \frac{{ -2 \sqrt x }}{{x + \sqrt x + 1}}\)
Đáp án: A
Lời giải chi tiết:
\(\begin{array}{l}\,\,\,T = \frac{{\sqrt x + 1}}{{x - 1}} - \frac{{x + 2}}{{x\sqrt x - 1}} - \frac{{\sqrt x + 1}}{{x + \sqrt x + 1}}\,\,\,\,\,\left( {DK:\,\,x \ge 0,\,\,x \ne 1} \right)\\\,\,\,\,\,\,\,\,\,\,\, = \frac{{\sqrt x + 1}}{{(\sqrt x - 1)(\sqrt x + 1)}} - \frac{{x + 2}}{{(\sqrt x - 1)(x + \sqrt x + 1)}} - \frac{{\sqrt x + 1}}{{x + \sqrt x + 1}}\\\,\,\,\,\,\,\,\,\,\, = \frac{1}{{\sqrt x - 1}} - \frac{{x + 2}}{{(\sqrt x - 1)(x + \sqrt x + 1)}} - \frac{{\sqrt x + 1}}{{x + \sqrt x + 1}}\\\,\,\,\,\,\,\,\,\,\, = \frac{{x + \sqrt x + 1 - (x + 2) - (\sqrt x + 1)(\sqrt x - 1)}}{{(\sqrt x - 1)(x + \sqrt x + 1)}}\\\,\,\,\,\,\,\,\,\,\, = \frac{{x + \sqrt x + 1 - x - 2 - (x - 1)}}{{(\sqrt x - 1)(x + \sqrt x + 1)}}\\\,\,\,\,\,\,\,\,\, = \frac{{\sqrt x - 1 - x + 1}}{{(\sqrt x - 1)(x + \sqrt x + 1)}}\\\,\,\,\,\,\,\,\, = \frac{{\sqrt x - x}}{{(\sqrt x - 1)(x + \sqrt x + 1)}}\\\,\,\,\,\,\,\,\, = \frac{{ - \sqrt x \left( {\sqrt x - 1} \right)}}{{(\sqrt x - 1)(x + \sqrt x + 1)}}\\\,\,\,\,\,\,\,\, = \frac{{ - \sqrt x }}{{x + \sqrt x + 1}}.\end{array}\)
Câu hỏi 10 :
Rút gọn biểu thức \(P = \frac{{a - 1}}{{\sqrt a + 1}} - \sqrt a + 11\) với \(a > 0.\)
- A \(P = 8.\)
- B \(P = 10.\)
- C \(P = 12.\)
- D \(P = 2\sqrt a .\)
Đáp án: B
Phương pháp giải:
Quy đồng mẫu số của biểu thức hoặc rút gọn phân thức bằng hằng đẳng thức \(a - 1 = \left( {\sqrt a + 1} \right)\left( {\sqrt a - 1} \right)\,\,\,\,\left( {a > 0} \right)\)
Lời giải chi tiết:
Rút gọn biểu thức \(P = \frac{{a - 1}}{{\sqrt a + 1}} - \sqrt a + 11\) với \(a > 0.\)
\(\begin{array}{l}P = \frac{{a - 1}}{{\sqrt a + 1}} - \sqrt a + 11\\\,\,\,\,\, = \frac{{\left( {\sqrt a + 1} \right)\left( {\sqrt a - 1} \right)}}{{\sqrt a + 1}} - \sqrt a + 11\\\,\,\,\,\, = \sqrt a - 1 - \sqrt a + 11\\\,\,\,\,\, = 10\end{array}\)
Vậy \(P = 10.\)
Chọn B.
Câu hỏi 11 :
Tìm khẳng định đúng trong các khẳng định sau:
- A \(\sqrt {\frac{6}{{{{\left( { - 5} \right)}^2}}}} = \frac{{\sqrt 6 }}{{ - 5}}\)
- B \(\sqrt {\frac{2}{{{a^2}}}} = \frac{{\sqrt 2 }}{a}\), với \(a \ne 0\)
- C \(\sqrt {\frac{6}{{{5^2}}}} = \frac{{\sqrt 6 }}{5}\)
- D \(\sqrt {\frac{{16}}{{{a^2}}}} = \frac{4}{a}\), với \(a \ne 0\)
Đáp án: C
Phương pháp giải:
Áp dụng công thức: \(\sqrt {{A^2}} = \left[ \begin{array}{l}A\,\,\,\,khi\,\,\,\,A \ge 0\\ - A\,\,\,\,khi\,\,\,\,A < 0\end{array} \right.\)
Lời giải chi tiết:
+) Đáp án A: \(\sqrt {\frac{6}{{{{\left( { - 5} \right)}^2}}}} = \frac{{\sqrt 6 }}{{ - \left( { - 5} \right)}} = \frac{{\sqrt 6 }}{5}\)\( \Rightarrow \) A sai.
+) Đáp án B: \(\sqrt {\frac{2}{a}} = \frac{{\sqrt 2 }}{{\left| a \right|}} = \left[ \begin{array}{l}\frac{{\sqrt 2 }}{a}\,\,\,\,khi\,\,\,\,a > 0\\\frac{{\sqrt 2 }}{{ - a}}\,\,\,\,khi\,\,\,\,a < 0\end{array} \right.\)\( \Rightarrow \) B sai.
+) Đáp án C: Đúng.
+) Đáp án D: \(\sqrt {\frac{{16}}{{{a^2}}}} = \frac{4}{{\left| a \right|}} = \left[ \begin{array}{l}\frac{4}{a}\,\,\,khi\,\,\,\,a > 0\\\frac{4}{{ - a}}\,\,\,\,khi\,\,\,\,a < 0\end{array} \right.\)\( \Rightarrow \) D sai.
Chọn C
Câu hỏi 12 :
Rút gọn biểu thức \(A = \frac{{x + \sqrt x + 1}}{{x + \sqrt x - 2}} + \frac{1}{{\sqrt x - 1}} + \frac{1}{{\sqrt x + 2}}\) với \(x \ge 0,\,\,x \ne 1.\)
- A \(A = \frac{{\sqrt x + 1}}{{\sqrt x - 1}}\)
- B \(A = \frac{{\sqrt x - 1}}{{\sqrt x + 1}}\)
- C \(A = \frac{{\sqrt x + 1}}{{\sqrt x + 2}}\)
- D \(A = \frac{{\sqrt x - 1}}{{\sqrt x + 2}}\)
Đáp án: A
Phương pháp giải:
Quy đồng và rút gọn biểu thức.
Lời giải chi tiết:
Điều kiện: \(x \ge 0,\,\,x \ne 1.\)
\(\begin{array}{l}A = \frac{{x + \sqrt x + 1}}{{x + \sqrt x - 2}} + \frac{1}{{\sqrt x - 1}} + \frac{1}{{\sqrt x + 2}}\,\,\\\,\,\,\, = \frac{{x + \sqrt x + 1 + \sqrt x + 2 + \sqrt x - 1}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 2} \right)}}\\\,\,\,\, = \frac{{x + 3\sqrt x + 2}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 2} \right)}}\\\,\,\,\, = \frac{{\left( {\sqrt x + 1} \right)\left( {\sqrt x + 2} \right)}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 2} \right)}} = \frac{{\sqrt x + 1}}{{\sqrt x - 1}}.\end{array}\)
Chọn A.
Câu hỏi 13 :
Rút gọn biểu thức \(A = \left[ {\frac{{2\left( {x - 2\sqrt x + 1} \right)}}{{x - 4}} - \frac{{2\sqrt x - 1}}{{\sqrt x + 2}}} \right]:\frac{{\sqrt x }}{{\sqrt x - 2}}\) với \(x > 0,\,\,\,x \ne 4.\)
- A \(A = \frac{1}{{\sqrt x - 2}}\)
- B \(A = \frac{1}{{\sqrt x}}\)
- C \(A = \frac{\sqrt x}{{\sqrt x + 2}}\)
- D \(A = \frac{1}{{\sqrt x + 2}}\)
Đáp án: D
Phương pháp giải:
Quy đồng mẫu các phân thức sau đó rút gọn biểu thức.
Lời giải chi tiết:
\(A = \left[ {\frac{{2\left( {x - 2\sqrt x + 1} \right)}}{{x - 4}} - \frac{{2\sqrt x - 1}}{{\sqrt x + 2}}} \right]:\frac{{\sqrt x }}{{\sqrt x - 2}}\) với \(x > 0;x \ne 4\)
\(\begin{array}{l}A = \left[ {\frac{{2\left( {x - 2\sqrt x + 1} \right)}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}} - \frac{{\left( {2\sqrt x - 1} \right)\left( {\sqrt x - 2} \right)}}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x - 2} \right)}}} \right]:\frac{{\sqrt x }}{{\sqrt x - 2}}\\\,\,\,\,\, = \frac{{2x - 4\sqrt x + 2 - 2x + \sqrt x + 4\sqrt x - 2}}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x - 2} \right)}}.\frac{{\sqrt x - 2}}{{\sqrt x }}\\\,\,\,\,\, = \frac{{\sqrt x }}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x - 2} \right)}}.\frac{{\sqrt x - 2}}{{\sqrt x }} = \frac{1}{{\sqrt x + 2}}\end{array}\)
Vậy \(A = \frac{1}{{\sqrt x + 2}}\).
Chọn D.
Câu hỏi 14 :
Rút gọn biểu thức sau: \(A = \frac{{4 + \sqrt 8 + \sqrt 2 - \sqrt 3 - \sqrt 6 }}{{2 + \sqrt 2 - \sqrt 3 }}.\)
- A \(A = 1 + \sqrt 2 \)
- B \(A = 1 - \sqrt 2 \)
- C \(A = 1 + \sqrt 3 \)
- D \(A = 1 - \sqrt 3 \)
Đáp án: A
Phương pháp giải:
Sử dụng công thức \(\sqrt {{A^2}B} = \left| A \right|\sqrt B = \left\{ \begin{array}{l}A\sqrt B \,\,\,khi\,\,\,A \ge 0\\ - A\sqrt B \,\,\,khi\,\,\,A < 0\end{array} \right.;\,\,\sqrt {AB} = \sqrt A .\sqrt B \) rồi đặt nhân tử chung của tử số và rút gọn biểu thức.
Lời giải chi tiết:
\(\begin{array}{l}A = \frac{{4 + \sqrt 8 + \sqrt 2 - \sqrt 3 - \sqrt 6 }}{{2 + \sqrt 2 - \sqrt 3 }} = \frac{{4 + 2\sqrt 2 + \sqrt 2 - \sqrt 3 - \sqrt {2.3} }}{{2 + \sqrt 2 - \sqrt 3 }}\\\,\,\,\,\, = \frac{{4 + 3\sqrt 2 - \sqrt 3 - \sqrt {2.3} }}{{2 + \sqrt 2 - \sqrt 3 }} = \frac{{\left( {2 + \sqrt 2 - \sqrt 3 } \right) + \left( {2\sqrt 2 + 2 - \sqrt {2.3} } \right)}}{{2 + \sqrt 2 - \sqrt 3 }}\\\,\,\,\,\, = \frac{{2 + \sqrt 2 - \sqrt 3 }}{{2 + \sqrt 2 - \sqrt 3 }} + \frac{{\sqrt 2 \left( {2 + \sqrt 2 - \sqrt 3 } \right)}}{{2 + \sqrt 2 - \sqrt 3 }} = 1 + \sqrt 2 \end{array}\)
Vậy \(A = 1 + \sqrt 2 \).
Chọn A.
Câu hỏi 15 :
Cho hai biểu thức: \(A = \dfrac{{x\sqrt x - 1}}{{x - \sqrt x }} - \dfrac{{x\sqrt x + 1}}{{x + \sqrt x }} + \dfrac{{2\left( {x + 1} \right)}}{{\sqrt x }}\) và \(B = \sqrt x + 1 + \dfrac{x}{{\sqrt x - 1}}\) với \(x > 0;x \ne 1\).
Câu 1:
Rút gọn biểu thức \(A\).
- A \(A = 2\sqrt x + 2 + \dfrac{\sqrt{2}}{{\sqrt x }}\)
- B \(A = \sqrt x + 2 + \dfrac{2}{{\sqrt x }}\)
- C \(A = 2\sqrt x + 2 + \dfrac{2}{{\sqrt x }}\)
- D \(A = 2\sqrt x + 1 + \dfrac{2}{{\sqrt x }}\)
Đáp án: C
Phương pháp giải:
Sử dụng các hằng đẳng thức \({a^3} \pm {b^3} = \left( {a \pm b} \right)\left( {{a^2} \mp ab + {b^2}} \right)\). Rút gọn từng phân thức (nếu được), sau đó quy đồng và rút gọn biểu thức.
Lời giải chi tiết:
\(A = \dfrac{{x\sqrt x - 1}}{{x - \sqrt x }} - \dfrac{{x\sqrt x + 1}}{{x + \sqrt x }} + \dfrac{{2\left( {x + 1} \right)}}{{\sqrt x }}\) với \(x > 0,\,\,x \ne 1.\)
\(\begin{array}{l}A = \dfrac{{{{\left( {\sqrt x } \right)}^3} - 1}}{{\sqrt x \left( {\sqrt x - 1} \right)}} - \dfrac{{{{\left( {\sqrt x } \right)}^3} + 1}}{{\sqrt x \left( {\sqrt x + 1} \right)}} + \dfrac{{2\left( {x + 1} \right)}}{{\sqrt x }}\\A = \dfrac{{\left( {\sqrt x - 1} \right)\left( {x + \sqrt x + 1} \right)}}{{\sqrt x \left( {\sqrt x - 1} \right)}} - \dfrac{{\left( {\sqrt x + 1} \right)\left( {x - \sqrt x + 1} \right)}}{{\sqrt x \left( {\sqrt x + 1} \right)}} + \dfrac{{2\left( {x + 1} \right)}}{{\sqrt x }}\\A = \dfrac{{x + \sqrt x + 1}}{{\sqrt x }} - \dfrac{{x - \sqrt x + 1}}{{\sqrt x }} + \dfrac{{2\left( {x + 1} \right)}}{{\sqrt x }}\\A = \dfrac{{x + \sqrt x + 1 - \left( {x - \sqrt x + 1} \right) + 2x + 2}}{{\sqrt x }}\\A = \dfrac{{2x + 2\sqrt x + 2}}{{\sqrt x }}\\A = 2\sqrt x + 2 + \dfrac{2}{{\sqrt x }}\end{array}\)
Vậy \(A = 2\sqrt x + 2 + \dfrac{2}{{\sqrt x }}\) với \(x > 0,\,\,x \ne 1.\)
Câu 2:
Tìm \(x\) để \(A = B\).
- A \(x = 4\)
- B \(x = -4\)
- C \(x = 2\)
- D \(x = -2\)
Đáp án: A
Phương pháp giải:
Quy đồng, rút gọn và giải phương trình, chú ý điều kiện xác định và đối chiếu nghiệm.
Lời giải chi tiết:
ĐKXĐ: \(x > 0,x \ne 1\)
\(\begin{array}{l}A = B\\ \Leftrightarrow 2\sqrt x + 2 + \dfrac{2}{{\sqrt x }} = \sqrt x + 1 + \dfrac{x}{{\sqrt x - 1}}\\ \Leftrightarrow \sqrt x + 1 + \dfrac{2}{{\sqrt x }} - \dfrac{x}{{\sqrt x - 1}} = 0\\ \Leftrightarrow \dfrac{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right).\sqrt x + 2\left( {\sqrt x - 1} \right) - x.\sqrt x }}{{\sqrt x \left( {\sqrt x - 1} \right)}} = 0\\ \Leftrightarrow \sqrt x .\left( {x - 1} \right) + 2\sqrt x - 2 - x\sqrt x = 0\\ \Leftrightarrow x\sqrt x - \sqrt x + 2\sqrt x - 2 - x\sqrt x = 0\\ \Leftrightarrow \sqrt x - 2 = 0\\ \Leftrightarrow \sqrt x = 2\\ \Leftrightarrow x = 4\,\,\,\,\,\left( {tm} \right)\end{array}\)
Vậy \(x = 4\) thì \(A = B.\)
Câu hỏi 16 :
Cho biểu thức
\(A = \left( {{1 \over {\sqrt x }} - {{\sqrt x - 1} \over {x + 2\sqrt x }}} \right):\left( {{1 \over {\sqrt x + 2}} - {{\sqrt x + 1} \over {x - 4}}} \right)\)
a) Rút gọn biểu thức \(A.\)
b) Tìm giá trị của A khi \(x = 9 - 4\sqrt 5 \)
c) Tìm \(x\) để \(A < 0\)
- A a) \(A = {{2 - \sqrt x } \over {\sqrt x }}\);b) \(A = 2\sqrt 5 + 3\);
c) \(x > 4\) thì \(A < 0\)
- B a) \(A = {{2 + \sqrt x } \over {\sqrt x }}\);b) \(A = 2\sqrt 5 - 3\);
c) \(x > 4\) thì \(A < 0.\)
- C a) \(A = {{2 + \sqrt x } \over {\sqrt x }}\);b) \(A = 2\sqrt 5 - 3\);
c) \(x > 9\) thì \(A < 0.\)
- D a) \(A = {{2 - \sqrt x } \over {\sqrt x }}\);b) \(A = 2\sqrt 5 + 3\);
c) \(x > 9\) thì \(A < 0.\)
Đáp án: A
Phương pháp giải:
+) Tìm điều kiện xác định của biểu thức.
+) Quy đồng mẫu, biến đổi và rút gọn biểu thức.
+) Biến đổi \(x\) sau đó thay giá trị của \(x\) thỏa mãn điều kiện và tính giá trị của biểu thức.
+) Giải bất phương trình \(A < 0\) để tìm \(x,\) đối chiếu với điều kiện rồi kết luận.
Lời giải chi tiết:
a) Rút gọn biểu thức \(A.\)
Điều kiện \(x > 0,x \ne 4\)
\(\begin{array}{l}A = \left( {\frac{1}{{\sqrt x }} - \frac{{\sqrt x - 1}}{{x + 2\sqrt x }}} \right):\left( {\frac{1}{{\sqrt x + 2}} - \frac{{\sqrt x + 1}}{{x - 4}}} \right)\\\,\,\,\,\, = \left( {\frac{{\sqrt x + 2}}{{\sqrt x \left( {\sqrt x + 2} \right)}} - \frac{{\sqrt x - 1}}{{\sqrt x \left( {\sqrt x + 2} \right)}}} \right):\left( {\frac{{\sqrt x - 2}}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x - 2} \right)}} - \frac{{\sqrt x + 1}}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x - 2} \right)}}} \right)\\\,\,\,\, = \frac{3}{{\sqrt x \left( {\sqrt x + 2} \right)}}:\frac{{ - 3}}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x - 2} \right)}} = \frac{3}{{\sqrt x \left( {\sqrt x + 2} \right)}}.\frac{{\left( {\sqrt x + 2} \right)\left( {\sqrt x - 2} \right)}}{{ - 3}}\\\,\,\,\, = \frac{{2 - \sqrt x }}{{\sqrt x }}\end{array}\)
Vậy với \(x > 0,x \ne 4\) thì \(A = \frac{{2 - \sqrt x }}{{\sqrt x }}\) .
b) Tính giá trị khi \(x = 9 - 4\sqrt 5 \)
Điều kiện \(x > 0,x \ne 4\)
\(\begin{array}{l}x = 9 - 4\sqrt 5 = {\left( {\sqrt 5 } \right)^2} - 2.2.\sqrt 5 + {2^2} = {\left( {\sqrt 5 - 2} \right)^2}\\ \Rightarrow \sqrt x = \sqrt {{{\left( {\sqrt 5 - 2} \right)}^2}} = \left| {\sqrt 5 - 2} \right| = \sqrt 5 - 2\left( {do\,\,\sqrt 5 - 2 > 0\,} \right)\end{array}\)
Thay \(x = 9 - 4\sqrt 5 \,\,\,\left( {tm} \right)\) vào biểu thức ta được:
\(A = \frac{{2 - \sqrt x }}{{\sqrt x }} = \frac{{2 - \left( {\sqrt 5 - 2} \right)}}{{\sqrt 5 - 2}} = \frac{{4 - \sqrt 5 }}{{\sqrt 5 - 2}} = \frac{{\left( {4 - \sqrt 5 } \right)\left( {\sqrt 5 + 2} \right)}}{{{{\left( {\sqrt 5 } \right)}^2} - {2^2}}} = \frac{{4\sqrt 5 + 8 - 5 - 2\sqrt 5 }}{1} = 2\sqrt 5 + 3.\)
Vậy với \(x = 9 - 4\sqrt 5 \) thì \(A = 2\sqrt 5 + 3.\)
c) Tìm \(x\) để \(A < 0.\)
Điều kiện \(x > 0,x \ne 4\)
Ta có: \(A < 0 \Leftrightarrow \frac{{2 - \sqrt x }}{{\sqrt x }} < 0\)
Với \(x > 0,x \ne 4\) ta có: \(\sqrt x > 0\)
\( \Rightarrow \frac{{2 - \sqrt x }}{{\sqrt x }} < 0 \Leftrightarrow 2 - \sqrt x < 0 \Leftrightarrow \sqrt x > 2 \Leftrightarrow x > 4.\) thì \(2 - \sqrt x < 0 \Leftrightarrow \sqrt x > 2 \Leftrightarrow x > 4\)
Kết hợp với điều kiện ta được \(x > 4\) thì \(A < 0.\)
Câu hỏi 17 :
Cho biểu thức
\(A = \left( {1 - {{\sqrt x } \over {1 + \sqrt x }}} \right):\left( {{{\sqrt x + 3} \over {\sqrt x - 2}} + {{\sqrt x + 2} \over {3 - \sqrt x }} + {{\sqrt x + 2} \over {x - 5\sqrt x + 6}}} \right)\)
1.Rút gọn \(A.\)
2.Tìm \(x\) để \(A < 0.\)
- A 1) \(A = {{\sqrt x + 2} \over {\sqrt x + 1}}\);
2) \(0 \le x < 9\) thì \(A < 0.\)
- B 1) \(A = {{\sqrt x - 2} \over {\sqrt x - 1}}\);
2) \(0 \le x < 4\) thì \(A < 0.\)
- C 1) \(A = {{\sqrt x - 2} \over {\sqrt x + 1}}\);
2) \(0 \le x < 4\) thì \(A < 0.\)
- D 1) \(A = {{\sqrt x - 2} \over {\sqrt x - 1}}\);
2) \(0 \le x < 9\) thì \(A < 0.\)
Đáp án: C
Phương pháp giải:
+) Tìm điều kiện của \(x\) để biểu thức xác định.
+) Giải bất phương trình \(A < 0\) để tìm \(x,\) đối chiếu với điều kiện rồi kết luận.
Lời giải chi tiết:
a) Rút gọn biểu thức \(A.\)
Điều kiện: \(\left\{ \begin{array}{l}x \ge 0\\\sqrt x - 2 \ne 0\\3 - \sqrt x \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 0\\x \ne 4\\x \ne 9\end{array} \right..\)
\(\begin{array}{l}A = \left( {1 - \frac{{\sqrt x }}{{1 + \sqrt x }}} \right):\left( {\frac{{\sqrt x + 3}}{{\sqrt x - 2}} + \frac{{\sqrt x + 2}}{{3 - \sqrt x }} + \frac{{\sqrt x + 2}}{{x - 5\sqrt x + 6}}} \right)\\ = \frac{{1 + \sqrt x - \sqrt x }}{{1 + \sqrt x }}:\left( {\frac{{\sqrt x + 3}}{{\sqrt x - 2}} + \frac{{\sqrt x + 2}}{{3 - \sqrt x }} + \frac{{\sqrt x + 2}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x - 3} \right)}}} \right)\\ = \frac{1}{{1 + \sqrt x }}:\left( {\frac{{\left( {\sqrt x + 3} \right)\left( {\sqrt x - 3} \right)}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x - 3} \right)}} - \frac{{\left( {\sqrt x + 2} \right)\left( {\sqrt x - 2} \right)}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x - 3} \right)}} + \frac{{\sqrt x + 2}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x - 3} \right)}}} \right)\\ = \frac{1}{{1 + \sqrt x }}:\frac{{x - 9 - x + 4 + \sqrt x + 2}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x - 3} \right)}}\\ = \frac{1}{{1 + \sqrt x }}.\frac{{\left( {\sqrt x - 2} \right)\left( {\sqrt x - 3} \right)}}{{\sqrt x - 3}}\\ = \frac{{\sqrt x - 2}}{{\sqrt x + 1}}\end{array}\)
b) Tìm \(x\) để \(A < 0.\)
Với \(x \ge 0;x \ne 9;x \ne 4\) ta có: \(A = \frac{{\sqrt x - 2}}{{\sqrt x + 1}}\)
Ta có: \(A < 0 \Leftrightarrow \frac{{\sqrt x - 2}}{{\sqrt x + 1}} < 0\).
Vì \(\sqrt x + 1 > 0,\forall x \ge 0 \Rightarrow A < 0 \Leftrightarrow \sqrt x - 2 < 0 \Leftrightarrow \sqrt x < 2 \Leftrightarrow x < 4\)
Kết hợp với điều kiện \(x \ge 0;x \ne 9;x \ne 4\) ta được: \(0 \le x < 4\) thì \(A < 0.\)
Câu hỏi 18 :
Cho biểu thức \(P = \left( {{{x - 2} \over {x + 2\sqrt x }} + {1 \over {\sqrt x + 2}}} \right).{{\sqrt x + 1} \over {\sqrt x - 1}}\) với \(x > 0;x \ne 1\)
a) Chứng minh rằng \(P = {{\sqrt x + 1} \over {\sqrt x }}\)
b) Tìm \(x\) để \(2P = 2\sqrt x + 5.\)
- A b) \(x = {1 \over 8}\)
- B b) \(x = {1 \over 4}\)
- C b) \(x = {1 \over 5}\)
- D b) \(x = {1 \over 2}\)
Đáp án: B
Phương pháp giải:
+) Quy đồng mẫu các phân thức và biến đổi, rút gọn biểu thức.
+) Giải phương trình \(2P = 2\sqrt x + 5,\) tìm \(x\) sau đó đối chiếu với điều kiện rồi kết luận.
Lời giải chi tiết:
a) Chứng minh rằng \(P = \frac{{\sqrt x + 1}}{{\sqrt x }}\)
Điều kiện: \(x > 0,x \ne 1\)
\(\begin{array}{l}P = \left( {\frac{{x - 2}}{{x + 2\sqrt x }} + \frac{1}{{\sqrt x + 2}}} \right).\frac{{\sqrt x + 1}}{{\sqrt x - 1}}\, = \left( {\frac{{x - 2}}{{\sqrt x \left( {\sqrt x + 2} \right)}} + \frac{1}{{\sqrt x + 2}}} \right).\frac{{\sqrt x + 1}}{{\sqrt x - 1}}\\\,\,\,\,\, = \left( {\frac{{x - 2}}{{\sqrt x \left( {\sqrt x + 2} \right)}} + \frac{{\sqrt x }}{{\sqrt x \left( {\sqrt x + 2} \right)}}} \right).\frac{{\sqrt x + 1}}{{\sqrt x - 1}} = \frac{{x - 2 + \sqrt x }}{{\sqrt x \left( {\sqrt x + 2} \right)}}.\frac{{\sqrt x + 1}}{{\sqrt x - 1}}\\\,\,\,\, = \frac{{x + 2\sqrt x - \sqrt x - 2}}{{\sqrt x \left( {\sqrt x + 2} \right)}}.\frac{{\sqrt x + 1}}{{\sqrt x - 1}} = \frac{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 2} \right)}}{{\sqrt x \left( {\sqrt x + 2} \right)}}.\frac{{\sqrt x + 1}}{{\sqrt x - 1}}\\\,\,\,\, = \frac{{\sqrt x + 1}}{{\sqrt x }}.\end{array}\)
Vậy với \(x > 0,x \ne 1\) ta có \(P = \frac{{\sqrt x + 1}}{{\sqrt x }}.\)
b) Tìm \(x\) để \(2P = 2\sqrt x + 5\)
Điều kiện: \(x > 0,x \ne 1\)
\(\begin{array}{l}\,\,\,\,\,\,2P = 2\sqrt x + 5 \Leftrightarrow 2.\frac{{\sqrt x + 1}}{{\sqrt x }} = 2\sqrt x + 5\\ \Leftrightarrow 2\sqrt x + 2 = 2x + 5\sqrt x \Leftrightarrow 2x + 3\sqrt x - 2 = 0\\ \Leftrightarrow 2x - \sqrt x + 4\sqrt x - 2 = 0 \Leftrightarrow \sqrt x \left( {2\sqrt x - 1} \right) + 2\left( {2\sqrt x - 1} \right) = 0\\ \Leftrightarrow \left( {2\sqrt x - 1} \right)\left( {\sqrt x + 2} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}\sqrt x = \frac{1}{2}\\\sqrt x = - 2\,\,\,\,\left( {VN} \right)\end{array} \right. \Leftrightarrow x = \frac{1}{4}\,\,\,\left( {tm} \right)\end{array}\)
Vậy \(x = \frac{1}{4}\) thì \(2P = 2\sqrt x + 5.\)
Câu hỏi 19 :
Cho biểu thức \(P = \left( {{{2\sqrt x } \over {\sqrt x + 3}} + {{\sqrt x } \over {\sqrt x - 3}} - {{3x + 3} \over {x - 9}}} \right):\left( {{{2\sqrt x - 2} \over {\sqrt x - 3}} - 1} \right)\)
a. Rút gọn \(P.\)
b. Tính giá trị của \(P\) biết \(x = {{3 - \sqrt 5 } \over 2}\)
c. Tìm \(x\) để \(P < - {1 \over 2}\)
- A a) \(P = {{ 3} \over {\sqrt x + 3}}\);
b) \(P={{\left( {\sqrt 5 - 5} \right)} \over {10}}\)
c) \(0 \le x < 9\) thì \(P < {{ - 1} \over 2}\)
- B a) \(P = {{ - 3} \over {\sqrt x - 3}}\);
b) \(P={{3\left( {\sqrt 5 - 5} \right)} \over {10}}\)
c) \( x < 9\) thì \(P < {{ - 1} \over 2}\)
- C a) \(P = {{ - 3} \over {\sqrt x + 3}}\);
b) \(P={{3\left( {\sqrt 5 + 5} \right)} \over {20}}\)
c) \(0 \le x < 9\) thì \(P < {{ - 1} \over 2}\)
- D a) \(P = {{ - 3} \over {\sqrt x + 3}}\);
b) \(P={{3\left( {\sqrt 5 - 5} \right)} \over {10}}\)
c) \(0 \le x < 9\) thì \(P < {{ - 1} \over 2}\)
Đáp án: D
Phương pháp giải:
+) Tìm điều kiện xác định của biểu thức.
+) Quy đồng mẫu các phân thức, biến đổi và rút gọn biểu thức.
+) Thay giá trị \(x\,\,\left( {tmdk} \right)\) vào biểu thức đã được rút gọn và tính giá trị của biểu thức.
+) Giải bất phương trình \(P < - \frac{1}{2},\) tìm \(x\) sau đó đối chiếu với điều kiện rồi kết luận.
Lời giải chi tiết:
a) Rút gọn \(P.\)
Điều kiện xác định: \(x \ge 0,x \ne 9\)
\(\begin{array}{l}P = \left( {\frac{{2\sqrt x }}{{\sqrt x + 3}} + \frac{{\sqrt x }}{{\sqrt x - 3}} - \frac{{3x + 3}}{{x - 9}}} \right):\left( {\frac{{2\sqrt x - 2}}{{\sqrt x - 3}} - 1} \right)\\ = \left( {\frac{{2\sqrt x \left( {\sqrt x - 3} \right)}}{{\left( {\sqrt x + 3} \right)\left( {\sqrt x - 3} \right)}} + \frac{{\sqrt x \left( {\sqrt x + 3} \right)}}{{\left( {\sqrt x + 3} \right)\left( {\sqrt x - 3} \right)}} - \frac{{3x + 3}}{{\left( {\sqrt x + 3} \right)\left( {\sqrt x - 3} \right)}}} \right):\left( {\frac{{2\sqrt x - 2}}{{\sqrt x - 3}} - \frac{{\sqrt x - 3}}{{\sqrt x - 3}}} \right)\\ = \frac{{2x - 6\sqrt x + x + 3\sqrt x - 3x - 3}}{{\left( {\sqrt x + 3} \right)\left( {\sqrt x - 3} \right)}}:\frac{{2\sqrt x - 2 - \sqrt x + 3}}{{\sqrt x - 3}}\\ = \frac{{ - 3\left( {\sqrt x + 1} \right)}}{{\left( {\sqrt x + 3} \right)\left( {\sqrt x - 3} \right)}}.\frac{{\sqrt x - 3}}{{\sqrt x + 1}}\\ = \frac{{ - 3}}{{\sqrt x + 3}}.\end{array}\)
b) Tính giá trị của biểu thức \(P\) biết \(x = \frac{{3 - \sqrt 5 }}{2}\)
Ta có: \(x = \frac{{3 - \sqrt 5 }}{2}\,\,\,\left( {tmdk} \right) \Rightarrow \sqrt x = \sqrt {\frac{{3 - \sqrt 5 }}{2}} = \frac{{\sqrt {6 - 2\sqrt 5 } }}{2} = \frac{{\sqrt {{{\left( {\sqrt 5 - 1} \right)}^2}} }}{2} = \frac{{\sqrt 5 - 1}}{2}\)
Khi đó ta có: \(P = \frac{{ - 3}}{{\sqrt x + 3}} = \frac{{ - 3}}{{\frac{{\sqrt 5 - 1}}{2} + 3}} = \frac{{ - 6}}{{\sqrt 5 + 5}} = \frac{{3\left( {\sqrt 5 - 5} \right)}}{{10}}\)
c) Tìm \(x\) để \(P < \frac{{ - 1}}{2}\)
Điều kiện xác định: \(x \ge 0,x \ne 9\)
Ta có: \(P = \frac{{ - 3}}{{\sqrt x + 3}} < \frac{{ - 1}}{2} \Leftrightarrow \frac{3}{{\sqrt x + 3}} > \frac{1}{2} \Leftrightarrow \frac{6}{{2\left( {\sqrt x + 3} \right)}} - \frac{{\sqrt x + 3}}{{2\left( {\sqrt x + 3} \right)}} > 0 \Leftrightarrow \frac{{3 - \sqrt x }}{{2\left( {\sqrt x + 3} \right)}} > 0\)
Với \(x \ge 0,x \ne 9\) ta có: \(2\left( {\sqrt x + 3} \right) > 0\) .
Khi đó để \(P < \frac{{ - 1}}{2} \Leftrightarrow 3 - \sqrt x > 0 \Leftrightarrow \sqrt x < 3 \Leftrightarrow x < 9.\)
Vậy kết hợp điều kiện ta được: \(0 \le x < 9\) thì \(P < \frac{{ - 1}}{2}.\)
Câu hỏi 20 :
Cho biểu thức \(P = 1:\left( {{{x + 2} \over {x\sqrt x - 1}} + {{\sqrt x + 1} \over {x + \sqrt x + 1}} - {{\sqrt x + 1} \over {x - 1}}} \right)\)
a. Rút gọn \(P.\)
b. Hãy so sánh \(P\) với \(3.\)
- A a) \(P = {{x - \sqrt x + 1} \over {\sqrt x }}\);
b) \(P \geq 3\)
- B a) \(P = {{x + \sqrt x + 1} \over {\sqrt x }}\);
b) \(P<3\)
- C a) \(P = {{x + \sqrt x + 1} \over {\sqrt x }}\);
b) \(P > 3\)
- D a) \(P = {{x - \sqrt x + 1} \over {\sqrt x }}\);
b) \(P \leq 3\)
Đáp án: C
Phương pháp giải:
+) Đặt điều kiện xác định của biểu thức.
+) Quy đồng mẫu, biến đổi các biểu thức sau đó rút gọn biểu thức đã cho.
+) Xét hiệu \(P - 3,\) so sánh hiệu đó với \(0\) rồi kết luận.
Lời giải chi tiết:
a) Rút gọn \(P.\)
Điều kiện xác định: \(x \ne 1;x > 0\)
\(\begin{array}{l}P = 1:\left( {\frac{{x + 2}}{{x\sqrt x - 1}} + \frac{{\sqrt x + 1}}{{x + \sqrt x + 1}} - \frac{{\sqrt x + 1}}{{x - 1}}} \right)\\ = 1:\left( {\frac{{x + 2}}{{\left( {\sqrt x - 1} \right)\left( {x + \sqrt x + 1} \right)}} + \frac{{\sqrt x + 1}}{{\left( {x + \sqrt x + 1} \right)}} - \frac{{\sqrt x + 1}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}}} \right)\\ = 1:\frac{{\left( {x + 2} \right)\left( {\sqrt x + 1} \right) + {{\left( {\sqrt x + 1} \right)}^2}\left( {\sqrt x - 1} \right) - \left( {\sqrt x + 1} \right)\left( {x + \sqrt x + 1} \right)}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)\left( {x + \sqrt x + 1} \right)}}\\ = 1:\frac{{x\sqrt x + x + 2\sqrt x + 2 + x\sqrt x + x - \sqrt x - 1 - \left( {x\sqrt x + x + \sqrt x + x + \sqrt x + 1} \right)}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)\left( {x + \sqrt x + 1} \right)}}\\ = \frac{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)\left( {x + \sqrt x + 1} \right)}}{{x\sqrt x - \sqrt x }}\\ = \frac{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)\left( {x + \sqrt x + 1} \right)}}{{\sqrt x \left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}}\\ = \frac{{x + \sqrt x + 1}}{{\sqrt x }}.\end{array}\)
b) So sánh \(P\) với \(3.\)
Điều kiện xác định: \(x \ne 1;x > 0\)
Xét hiệu: \(P - 3 = \frac{{x + \sqrt x + 1}}{{\sqrt x }} - 3 = \frac{{x + \sqrt x + 1 - 3\sqrt x }}{{\sqrt x }} = \frac{{{{\left( {\sqrt x - 1} \right)}^2}}}{{\sqrt x }}\)
Với \(x \ne 1;x > 0\) ta có: \(\sqrt x > 0;\,\,{\left( {\sqrt x - 1} \right)^2} > 0 \Rightarrow P - 3 > 0 \Leftrightarrow P > 3.\)
Câu hỏi 21 :
Cho biểu thức \( P = {{15\sqrt x - 11} \over {x + 2\sqrt x - 3}} + {{3\sqrt x - 2} \over {1 - \sqrt x }} - {{2\sqrt x + 3} \over {\sqrt x + 3}}\)
a) Rút gọn \(P.\)
b) Tìm các giá trị của \(x\) để \( P = {1 \over 2}.\)
c) Chứng minh \( P \le {2 \over 3}.\)
- A a) \(P=\frac{-5\sqrt{x}+2}{\sqrt{x}+3}.\)
b) \(x=\frac{1}{121}.\)
c) \( x \ge 0, \, x \ne 1\)
- B a) \(P=\frac{-5\sqrt{x}+2}{\sqrt{x}+3}.\)
b) \(x=\frac{1}{11}.\)
c) \( x \ge 0, \, x \ne 1\)
- C a) \(P=\frac{-5\sqrt{x}+2}{\sqrt{x}+3}.\)
b) \(x=\frac{1}{121}.\)
c) \( x > 0, \, x \ne 1\)
- D a) \(P=\frac{-5\sqrt{x}+2}{\sqrt{x}+3}.\)
b) \(x=\frac{1}{11}.\)
c) \( x > 0, \, x \ne 1\)
Đáp án: A
Phương pháp giải:
+) Tìm điều kiện xác định của biểu thức.
+) Quy đồng mẫu các phân thức, biến đổi và rút gọn biểu thức.
+) Giải phương trình \(P = \frac{1}{2},\) tìm \(x\) rồi đối chiều với điều kiện sau đó kết luận.
+) Dựa vào điều kiện của \(x\) để chứng mình \(P \le \frac{2}{3}.\)
Lời giải chi tiết:
\(P = \frac{{15\sqrt x - 11}}{{x + 2\sqrt x - 3}} + \frac{{3\sqrt x - 2}}{{1 - \sqrt x }} - \frac{{2\sqrt x + 3}}{{\sqrt x + 3}}\)
a) Rút gọn \(P.\)
Điều kiện \(x \ge 0,x \ne 1\)
\(\begin{array}{l}P = \frac{{15\sqrt x - 11}}{{x + 2\sqrt x - 3}} + \frac{{3\sqrt x - 2}}{{1 - \sqrt x }} - \frac{{2\sqrt x + 3}}{{\sqrt x + 3}}\\ = \frac{{15\sqrt x - 11}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 3} \right)}} - \frac{{3\sqrt x - 2}}{{\sqrt x - 1}} - \frac{{2\sqrt x + 3}}{{\sqrt x + 3}}\\ = \frac{{15\sqrt x - 11}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 3} \right)}} - \frac{{\left( {3\sqrt x - 2} \right)\left( {\sqrt x + 3} \right)}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 3} \right)}} - \frac{{\left( {2\sqrt x + 3} \right)\left( {\sqrt x - 1} \right)}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 3} \right)}}\\ = \frac{{15\sqrt x - 11 - \left( {3x + 9\sqrt x - 2\sqrt x - 6} \right) - \left( {2x - 2\sqrt x + 3\sqrt x - 3} \right)}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 3} \right)}}\\ = \frac{{15\sqrt x - 11 - 3x - 7\sqrt x + 6 - 2x - \sqrt x + 3}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 3} \right)}}\\ = \frac{{ - 5x + 7\sqrt x - 2}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 3} \right)}} = \frac{{\left( { - 5\sqrt x + 2} \right)\left( {\sqrt x - 1} \right)}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 3} \right)}} = \frac{{ - 5\sqrt x + 2}}{{\sqrt x + 3}}.\end{array}\)
b) Tìm các giá trị của \(x\) để \(P = \frac{1}{2}.\)
Với điều kiện \(x \ge 0,x \ne 1.\) ta có:
\(\begin{array}{l}P = \frac{1}{2} \Leftrightarrow \frac{{ - 5\sqrt x + 2}}{{\sqrt x + 3}} = \frac{1}{2} \Leftrightarrow 2\left( { - 5\sqrt x + 2} \right) = \sqrt x + 3\\ \Leftrightarrow - 10\sqrt x + 4 - \sqrt x - 3 = 0\\ \Leftrightarrow - 11\sqrt x = - 1 \Leftrightarrow x = \frac{1}{{121}}\,\,\,\,\left( {tm} \right).\end{array}\)
Vậy \(x = \frac{1}{{121}}\) thì \(P = \frac{1}{2}.\)
c) Chứng minh \(P \le \frac{2}{3}\)
Ta có: \(P = \frac{{ - 5\sqrt x + 2}}{{\sqrt x + 3}}\)
Với \(x \ge 0,\,\,x \ne 1\) ta có: \(\sqrt x + 3 \ge 3\)
\(5\sqrt x \ge 0 \Rightarrow - 5\sqrt x \le 0 \Rightarrow - 5\sqrt x + 2 \le 2\)
Khi đó ta có: \(P \le \frac{2}{3}\)
Vậy \(x \ge 0,x \ne 1\) thì \(P \le \frac{2}{3}.\)
Câu hỏi 22 :
Cho biểu thức \(P = \left( {{1 \over {\sqrt x + 1}} - {{2\sqrt x - 2} \over {x\sqrt x - \sqrt x + x - 1}}} \right):\left( {{1 \over {\sqrt x - 1}} - {2 \over {x - 1}}} \right)\)
a. Rút gọn \(P.\)
b.Tính giá trị của \(P\) khi \(x = 7 - 4\sqrt 3. \)
- A a)\(P = {{\sqrt x - 1} \over {\sqrt x + 1}}\);
b) \(P={{- \sqrt 3 } \over 3}\)
- B a)\(P = {{\sqrt x + 1} \over {\sqrt x - 1}}\);
b) \(P={{3 - 2\sqrt 3 } \over 3}\)
- C a)\(P = {{\sqrt x - 1} \over {\sqrt x + 1}}\);
b) \(P={{3 + 2\sqrt 3 } \over 3}\)
- D a)\(P = {{\sqrt x + 1} \over {\sqrt x - 1}}\);
b) \(P={{3 + 2\sqrt 3 } \over 3}\)
Đáp án: A
Phương pháp giải:
+) Tìm điều kiện xác định của biểu thức.
+) Quy đồng mẫu các phân thức, biến đổi và rút gọn biểu thức.
+) Biến đổi \(x,\) thay giá trị \(x = 7 - 4\sqrt 3 \,\,\,\left( {tm} \right)\) vào biểu thức \(P\) rồi tính giá trị biểu thức.
Lời giải chi tiết:
a) Rút gọn \(P.\)
Điều kiện: \(x \ge 0;x \ne 1\)
\(\begin{array}{l}P = \left( {\frac{1}{{\sqrt x + 1}} - \frac{{2\sqrt x - 2}}{{x\sqrt x - \sqrt x + x - 1}}} \right):\left( {\frac{1}{{\sqrt x - 1}} - \frac{2}{{x - 1}}} \right)\\ = \left( {\frac{1}{{\sqrt x + 1}} - \frac{{2\left( {\sqrt x - 1} \right)}}{{\sqrt x \left( {x - 1} \right) + x - 1}}} \right):\left( {\frac{1}{{\sqrt x - 1}} - \frac{2}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}} \right)\\ = \left( {\frac{1}{{\left( {\sqrt x + 1} \right)}} - \frac{{2\left( {\sqrt x - 1} \right)}}{{\left( {x - 1} \right)\left( {\sqrt x + 1} \right)}}} \right):\left( {\frac{{\sqrt x + 1}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}} - \frac{2}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}} \right)\\ = \left( {\frac{{\sqrt x + 1}}{{{{\left( {\sqrt x + 1} \right)}^2}}} - \frac{2}{{{{\left( {\sqrt x + 1} \right)}^2}}}} \right):\frac{{\sqrt x - 1}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}\\ = \frac{{\sqrt x - 1}}{{{{\left( {\sqrt x + 1} \right)}^2}}}.\frac{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}{{\sqrt x - 1}}\\ = \frac{{\sqrt x - 1}}{{\sqrt x + 1}}.\end{array}\)
b) Tính giá trị của P khi \(x = 7 - 4\sqrt 3 \)
Khi \(x = 7 - 4\sqrt 3 = {\left( {2 - \sqrt 3 } \right)^2}\,\,\,\,\left( {tm} \right) \Rightarrow \sqrt x = \sqrt {{{\left( {2 - \sqrt 3 } \right)}^2}} = \left| {2 - \sqrt 3 } \right| = 2 - \sqrt 3 \)
Ta có: \(P = \frac{{2 - \sqrt 3 - 1}}{{2 - \sqrt 3 + 1}} = \frac{{1 - \sqrt 3 }}{{3 - \sqrt 3 }} = \frac{{\left( {1 - \sqrt 3 } \right)\left( {3 + \sqrt 3 } \right)}}{{{3^2} - 3}} = \frac{{ - 2\sqrt 3 }}{6} = \frac{{ - \sqrt 3 }}{3}.\)
Câu hỏi 23 :
Cho biểu thức \( A = \sqrt {x + 4\sqrt {x - 4} } + \sqrt {x - 4\sqrt {x - 4} } \)
a) Rút gọn \(A.\)
b) Tìm \(x\) để \(A = 4.\)
- A a) \( A = \left\{ \matrix{2\sqrt {x - 4} \,\,\,\,\,khi\,\,\,\,x \ge 8 \hfill \cr4\,\,\,\,khi\,\,\,4 \le x < 8. \hfill \cr} \right.\)
b) \( x = 8\)
- B a) \( A = \left\{ \matrix{2\sqrt {x - 4} \,\,\,\,\,khi\,\,\,\,x \ge 8 \hfill \cr4\,\,\,\,khi\,\,\,4 \le x < 8. \hfill \cr} \right.\)
b) \( 4 < x \le 8\)
- C a) \( A = \left\{ \matrix{2\sqrt {x - 4} \,\,\,\,\,khi\,\,\,\,x \ge 8 \hfill \cr4\,\,\,\,khi\,\,\,4 \le x < 8. \hfill \cr} \right.\)
b) \( x \geq 8\)
- D a) \( A = \left\{ \matrix{2\sqrt {x - 4} \,\,\,\,\,khi\,\,\,\,x \ge 8 \hfill \cr 4\,\,\,\,khi\,\,\,4 \le x < 8. \hfill \cr} \right.\)
b) \( 4 \le x \le 8\)
Đáp án: D
Phương pháp giải:
+) Tìm điều kiện xác định của biểu thức.
+) Quy đồng mẫu các phân thức, biến đổi và rút gọn biểu thức.
+) Giải phương trình \(A = 4,\) tìm \(x\) rồi đối chiều với điều kiện sau đó kết luận.
Lời giải chi tiết:
\(A = \sqrt {x + 4\sqrt {x - 4} } + \sqrt {x - 4\sqrt {x - 4} } \)
a) Rút gọn \(A.\)
Điều kiện \(x \ge 4\)
Ta có:
\(\begin{array}{l}A = \sqrt {x + 4\sqrt {x - 4} } + \sqrt {x - 4\sqrt {x - 4} } \\ = \sqrt {4 + x - 4 + 4\sqrt {x - 4} } + \sqrt {4 + x - 4 - 4\sqrt {x - 4} } \\ = \sqrt {{{\left( {\sqrt {x - 4} + 2} \right)}^2}} + \sqrt {{{\left( {\sqrt {x - 4} - 2} \right)}^2}} \\ = \left| {\sqrt {x - 4} + 2} \right| + \left| {\sqrt {x - 4} - 2} \right|\\ = \sqrt {x - 4} + 2 + \left| {\sqrt {x - 4} - 2} \right|\end{array}\)
TH1: \(\sqrt {x - 4} - 2 \ge 0 \Leftrightarrow x \ge 8.\) Ta có:\(A = \sqrt {x - 4} + 2 + \sqrt {x - 4} - 2 = 2\sqrt {x - 4} \)
TH2: \(\sqrt {x - 4} - 2 < 0 \Leftrightarrow x < 8\). Ta có: \(A = \sqrt {x - 4} + 2 - \sqrt {x - 4} + 2 = 4\)
Vậy \(x \ge 8\) thì \(A = 2\sqrt {x - 4} \)
Với \(4 \le x < 8\) thì \(A = 4.\)
b) Tìm \(x\) để \(A = 4.\)
Theo câu a) ta có TH1: Với \(4 \le x < 8\) thì \(A = 4.\)
Với TH2: \(x \ge 8\)
\(A = 4 \Leftrightarrow 2\sqrt {x - 4} = 4 \Leftrightarrow x - 4 = 4 \Leftrightarrow x = 8\)
Vậy \(x = 8\) thì \(A = 4.\)
Kết hợp 2 trường hợp ta được \(4 \le x \le 8\) thì \(A = 4.\)
Câu hỏi 24 :
Cho \( A = \left( {{{x - y} \over {\sqrt x - \sqrt y }} + {{\sqrt {{x^3}} - \sqrt {{y^3}} } \over {y - x}}} \right):{{{{\left( {\sqrt x - \sqrt y } \right)}^2} + \sqrt {xy} } \over {\sqrt x + \sqrt y }}\) Với \( x \ge 0, \, y \ge 0,x \ne y.\)
a) Rút gọn \(A.\)
b) Chứng minh rằng \(A \geq 0.\)
- A \(A={{\sqrt {xy} } \over {x + \sqrt {xy} + y}}.\)
- B \(A={{\sqrt {xy} } \over {x - \sqrt {xy} + y}}.\)
- C \(A={{xy } \over {x - \sqrt {xy} +y}}.\)
- D \(A={{xy } \over {x + \sqrt {xy} +y}}.\)
Đáp án: B
Phương pháp giải:
+) Tìm điều kiện xác định của biểu thức.
+) Quy đồng mẫu các phân thức, biến đổi và rút gọn biểu thức.
+) Dựa vào điều kiện của \(x\) để chứng mình \(A \ge 0.\)
Lời giải chi tiết:
a) Với \(x \ge 0,y \ge 0,x \ne y\). Ta có:
\(\begin{array}{l}A = \left( {\frac{{x - y}}{{\sqrt x - \sqrt y }} + \frac{{\sqrt {{x^3}} - \sqrt {{y^3}} }}{{y - x}}} \right):\frac{{{{\left( {\sqrt x - \sqrt y } \right)}^2} + \sqrt {xy} }}{{\sqrt x + \sqrt y }}\\ = \left( {\frac{{\left( {\sqrt x - \sqrt y } \right)\left( {\sqrt x + \sqrt y } \right)}}{{\sqrt x - \sqrt y }} - \frac{{\left( {\sqrt x - \sqrt y } \right)\left( {x + \sqrt {xy} + y} \right)}}{{\left( {\sqrt x - \sqrt y } \right)\left( {\sqrt x + \sqrt y } \right)}}} \right):\frac{{{{\left( {\sqrt x - \sqrt y } \right)}^2} + \sqrt {xy} }}{{\sqrt x + \sqrt y }}\\ = \left( {\sqrt x + \sqrt y - \frac{{x + \sqrt {xy} + y}}{{\sqrt x + \sqrt y }}} \right):\frac{{x - \sqrt {xy} + y}}{{\sqrt x + \sqrt y }}\\ = \frac{{{{\left( {\sqrt x + \sqrt y } \right)}^2} - x - \sqrt {xy} - y}}{{\sqrt x + \sqrt y }}.\frac{{\sqrt x + \sqrt y }}{{x - \sqrt {xy} + y}}\\ = \frac{{\sqrt {xy} }}{{x - \sqrt {xy} + y}}\end{array}\)
b) Ta có: \(x \ge 0,y \ge 0,x \ne y\) thì \(\sqrt {xy} \ge 0;x - \sqrt {xy} + y = {\left( {\sqrt x - \sqrt y } \right)^2} + \sqrt {xy} \ge 0\) .
Vậy \(A \ge 0\) với \(x \ge 0,y \ge 0,x \ne y\).
Câu hỏi 25 :
Cho biểu thức P = \(\frac{2\sqrt{x}-9}{x-5\sqrt{x}+6}-\frac{\sqrt{x}+3}{\sqrt{x}-2}+\frac{2\sqrt{x}+1}{\sqrt{x}-3}\) với \(x\ge 0;x\ne 4;x\ne 9\)
Rút gọn biểu thức P Tìm x để P = 5.Phương pháp giải:
Phương pháp:
* Các bước làm bài toán rút gọn biểu thức:
B1: Tìm ĐKXĐ của bài toán nếu đề bài chưa cho ĐKXĐ. Các biểu thức cần lấy ĐK là:
\(\begin{align} & +)\,\,\frac{1}{f\left( x \right)}\Rightarrow f\left( x \right)\ne 0. \\ & +)\,\,\sqrt{f\left( x \right)}\Rightarrow f\left( x \right)\ge 0. \\ & +)\,\,\frac{1}{\sqrt{f\left( x \right)}}\Rightarrow f\left( x \right)>0. \\\end{align}\)
B2: Tìm mẫu thức chung của biểu thức sau đó quy đồng mẫu các phân thức.
B3: Rút gọn biểu thức.
* Phương pháp làm câu b: Tìm x để \(P=a:\)
+) Ta cho biểu thức P vừa rút gọn được bằng giá trị a và giải phương trình tìm x.
+) Đối chiếu giá trị của x vừa tìm được với ĐKXĐ xem x có thỏa mãn không.
+) Nếu x thỏa mãn thì kết luận đó là giá trị cần tìm. Nếu x không thỏa mãn thì loại giá trị đó.
Lời giải chi tiết:
Giải:
Với \(x\ge 0;x\ne 4;x\ne 9\) ta có
\(\begin{align} & P=\frac{2\sqrt{x}-9-\left( \sqrt{x}+3 \right)\left( \sqrt{x}-3 \right)+\left( 2\sqrt{x}+1 \right)\left( \sqrt{x}-2 \right)}{\left( \sqrt{x}-2 \right)\left( \sqrt{x}-3 \right)} \\ & \,\,\,\,=\frac{2\sqrt{x}-9-\left( x-9 \right)+2x-3\sqrt{x}-2}{\left( \sqrt{x}-2 \right)\left( \sqrt{x}-3 \right)}=\frac{x-\sqrt{x}-2}{\left( \sqrt{x}-2 \right)\left( \sqrt{x}-3 \right)} \\ & \,\,\,\,=\frac{\left( \sqrt{x}+1 \right)\left( \sqrt{x}-2 \right)}{\left( \sqrt{x}-3 \right)\left( \sqrt{x}-2 \right)} \\ & \,\,\,\,=\frac{\sqrt{x}+1}{\sqrt{x}-3}. \\ \end{align}\)
Vậy \(P=\frac{\sqrt{x}+1}{\sqrt{x}-3}\) với \(x\ge 0;x\ne 4;x\ne 9\)
b. Theo câu a ta có \(P=\frac{\sqrt{x}+1}{\sqrt{x}-3}\) với \(x\ge 0;x\ne 4;x\ne 9\)
\(\begin{align} & \text{ P }=\text{ 5}\Leftrightarrow \frac{\sqrt{x}+1}{\sqrt{x}-3}=5 \\ & \Rightarrow \sqrt{x}+1=5\left( \sqrt{x}-3 \right) \\ & \Leftrightarrow \sqrt{x}+1=5\sqrt{x}-15 \\ & \Leftrightarrow 16=4\sqrt{x} \\ & \Leftrightarrow \sqrt{x}=\frac{16}{4}=4 \\ & \Leftrightarrow x=16\,\,\,\left( tm \right) \\ \end{align}\)
Vậy để P = 5 thì x = 16.
Câu hỏi 26 :
a) Tính: \(\sqrt {{{\left( {2 - \sqrt 5 } \right)}^2}} - \sqrt {\dfrac{8}{{7 - 3\sqrt 5 }}} \)
b) Rút gọn: \(A = \dfrac{x}{{\sqrt x - 1}} - \dfrac{{2x - \sqrt x }}{{x - \sqrt x }}\) (với \(x > 0{;^{}}x \ne 1\))
- A 3
- B 4
- C -5
- D 7
Đáp án: C
Lời giải chi tiết:
\(\begin{array}{l}
\sqrt {{{\left( {2 - \sqrt 5 } \right)}^2}} - \sqrt {\dfrac{8}{{7 - 3\sqrt 5 }}} \\
= \left| {2 - \sqrt 5 } \right| - \sqrt {\dfrac{{16}}{{14 - 6\sqrt 5 }}} \\
= \left| {2 - \sqrt 5 } \right| - \dfrac{{\sqrt {16} }}{{\sqrt {14 - 6\sqrt 5 } }}\\
= - \left( {2 - \sqrt 5 } \right) - \dfrac{4}{{\sqrt {{3^2} - 2.3.\sqrt 5 + {{\sqrt 5 }^2}} }}\left( {Do{\rm{ }}2 - \sqrt 5 < 0} \right)\\
= - 2 + \sqrt 5 - \dfrac{4}{{\sqrt {{{\left( {3 - \sqrt 5 } \right)}^2}} }}\\
= - 2 + \sqrt 5 - \dfrac{4}{{3 - \sqrt 5 }}\\
= - 2 + \sqrt 5 - \dfrac{{4.\left( {3 + \sqrt 5 } \right)}}{{\left( {3 - \sqrt 5 } \right)\left( {3 + \sqrt 5 } \right)}}\\
= - 2 + \sqrt 5 - \dfrac{{4.\left( {3 + \sqrt 5 } \right)}}{4}\\
= - 2 + \sqrt 5 - 3 - \sqrt 5 = - 5
\end{array}\)
b)
\(\begin{array}{l}
A = \dfrac{x}{{\sqrt x - 1}} - \dfrac{{2x - \sqrt x }}{{x - \sqrt x }}\\
= \dfrac{x}{{\sqrt x - 1}} - \dfrac{{\sqrt x \left( {2\sqrt x - 1} \right)}}{{\sqrt x \left( {\sqrt x - 1} \right)}}\\
= \dfrac{x}{{\sqrt x - 1}} - \dfrac{{2\sqrt x - 1}}{{\sqrt x - 1}}\\
= \dfrac{{x - 2\sqrt x + 1}}{{\sqrt x - 1}}\\
= \dfrac{{{{\left( {\sqrt x - 1} \right)}^2}}}{{\sqrt x - 1}} = \sqrt x - 1
\end{array}\)
Câu hỏi 27 :
a) Tính: \(A=\left( \frac{2}{3-\sqrt{5}}+\frac{1}{2-\sqrt{5}}-\frac{10}{2\sqrt{5}} \right).\left( 1-3\sqrt{5} \right)\)
b) Rút gọn biểu thức sau: \(P=\frac{\sqrt{x}}{2\sqrt{x}-3}+\frac{\sqrt{x}-2}{2\sqrt{x}+3}+\frac{15-4\sqrt{x}}{9-4x}\) (với \(x\ge 0{{;}^{{}}}^{{}}x\ne \frac{9}{4}\))
Lời giải chi tiết:
a) Ta có:
\(\begin{array}{l}A = \left( {\frac{2}{{3 - \sqrt 5 }} + \frac{1}{{2 - \sqrt 5 }} - \frac{{10}}{{2\sqrt 5 }}} \right).\left( {1 - 3\sqrt 5 } \right)\\ = \left( {\frac{{2\left( {3 + \sqrt 5 } \right)}}{{\left( {3 - \sqrt 5 } \right)\left( {3 + \sqrt 5 } \right)}} + \frac{{1.\left( {2 + \sqrt 5 } \right)}}{{\left( {2 + \sqrt 5 } \right)\left( {2 - \sqrt 5 } \right)}} - \frac{5}{{\sqrt 5 }}} \right).\left( {1 - 3\sqrt 5 } \right)\\ = \left( {\frac{{2\left( {3 + \sqrt 5 } \right)}}{4} + \frac{{2 + \sqrt 5 }}{{ - 1}} - \sqrt 5 } \right).\left( {1 - 3\sqrt 5 } \right)\\ = \left( {\frac{{3 + \sqrt 5 }}{2} - \frac{{2 + \sqrt 5 }}{1} - \sqrt 5 } \right).\left( {1 - 3\sqrt 5 } \right)\\ = \left( {\frac{{3 + \sqrt 5 - 2\left( {2 + \sqrt 5 } \right) - 2\sqrt 5 }}{2}} \right).\left( {1 - 3\sqrt 5 } \right)\\= \left( {\frac{{3 + \sqrt 5 - 4 - 2\sqrt 5 - 2\sqrt 5 }}{2}} \right).\left( {1 - 3\sqrt 5 } \right)\\ = - \left( {\frac{{ - 1 - 3\sqrt 5 }}{2}} \right).\left( {3\sqrt 5 - 1} \right)\\ = \left( {\frac{{3\sqrt 5 + 1}}{2}} \right).\left( {3\sqrt 5 - 1} \right)\\ = \frac{{\left( {3\sqrt 5 + 1} \right)\left( {3\sqrt 5 - 1} \right)}}{2}\\ = \frac{{44}}{2} = 22\end{array}\)
b) Ta có:
\(\begin{array}{l}P = \frac{{\sqrt x }}{{2\sqrt x - 3}} + \frac{{\sqrt x - 2}}{{2\sqrt x + 3}} + \frac{{15 - 4\sqrt x }}{{9 - 4x}}\\ = \frac{{\sqrt x }}{{2\sqrt x - 3}} + \frac{{\sqrt x - 2}}{{2\sqrt x + 3}} - \frac{{15 - 4\sqrt x }}{{4x - 9}}\\ = \frac{{\sqrt x }}{{2\sqrt x - 3}} + \frac{{\sqrt x - 2}}{{2\sqrt x + 3}} - \frac{{15 - 4\sqrt x }}{{\left( {2\sqrt x - 3} \right).\left( {2\sqrt x + 3} \right)}}\\ = \frac{{\sqrt x .\left( {2\sqrt x + 3} \right) + \left( {\sqrt x - 2} \right).\left( {2\sqrt x - 3} \right) - \left( {15 - 4\sqrt x } \right)}}{{\left( {2\sqrt x - 3} \right).\left( {2\sqrt x + 3} \right)}}\\ = \frac{{2x + 3\sqrt x + 2x - 3\sqrt x - 4\sqrt x + 6 - 15 + 4\sqrt x }}{{\left( {2\sqrt x - 3} \right).\left( {2\sqrt x + 3} \right)}}\\ = \frac{{4x - 9}}{{4x - 9}}\\ = 1\end{array}\)
Câu hỏi 28 :
Cho hai biểu thức: \(A\, = \,\frac{{2\sqrt x - 4}}{{\sqrt x - 1}}\) và \(B\, = \,\frac{{\sqrt x }}{{\sqrt x - 1}} + \frac{3}{{\sqrt x + 1}} - \frac{{6\sqrt x - 4}}{{x - 1}}\) với \(x \ge 0,\,\,x \ne 1.\)
1. Tính giá trị của A khi \(x = 4.\)
2. Rút gọn B.
3. So sánh A.B với 5.
- A 1. 0
2. \(\frac{{\sqrt x - 1}}{{\sqrt x + 1}}\)
3. A.B < 5
- B 1. 0
2. \(\frac{{\sqrt x + 1}}{{\sqrt x - 1}}\)
3. A.B < 5
- C 1. 0
2. \(\frac{{\sqrt x - 1}}{{\sqrt x + 1}}\)
3. A.B > 5
- D 1. 0
2. \(\frac{{\sqrt x + 1}}{{\sqrt x - 1}}\)
3. A.B > 5
Đáp án: A
Phương pháp giải:
+) Sử dụng hằng đẳng thức: \({a^2} - {b^2} = \left( {a - b} \right)\left( {a + b} \right)\).
+) Để so sánh a và b ta xét hiệu \(a - b\) .
Lời giải chi tiết:
Cho hai biểu thức: \(A\, = \,\frac{{2\sqrt x - 4}}{{\sqrt x - 1}}\) và \(B\, = \,\frac{{\sqrt x }}{{\sqrt x - 1}} + \frac{3}{{\sqrt x + 1}} - \frac{{6\sqrt x - 4}}{{x - 1}}\) với \(x \ge 0,\,\,x \ne 1.\)
1. Tính giá trị của A khi \(x = 4.\)
Khi \(x = 4\) thì \(A\, = \,\frac{{2\sqrt 4 - 4}}{{\sqrt 4 - 1}} = \frac{{2.2 - 4}}{{2 - 1}} = \frac{0}{1} = 0\)
2. Rút gọn B.
\(\begin{array}{l}B\, = \,\frac{{\sqrt x }}{{\sqrt x - 1}} + \frac{3}{{\sqrt x + 1}} - \frac{{6\sqrt x - 4}}{{x - 1}} = \frac{{\sqrt x \left( {\sqrt x + 1} \right)}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}} + \frac{{3\left( {\sqrt x - 1} \right)}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}} - \frac{{6\sqrt x - 4}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}\\\,\,\,\, = \frac{{x + \sqrt x + 3\sqrt x - 3 - 6\sqrt x + 4}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}} = \frac{{x - 2\sqrt x + 1}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}\\\,\,\,\, = \frac{{{{\left( {\sqrt x - 1} \right)}^2}}}{{x - 1}} = \frac{{\sqrt x - 1}}{{\sqrt x + 1}}.\end{array}\)
3. So sánh A.B với 5.
\(\begin{array}{l}A.B - 5 = \frac{{2\sqrt x - 4}}{{\sqrt x - 1}}.\frac{{\sqrt x - 1}}{{\sqrt x + 1}} - 5 = \frac{{2\sqrt x - 4}}{{\sqrt x + 1}} - 5\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{2\sqrt x - 4 - 5\sqrt x - 5}}{{\sqrt x + 1}} = \frac{{ - 3\sqrt x - 9}}{{\sqrt x + 1}}\end{array}\)
Có \(\sqrt x \ge 0\;\forall x \ge 0 \Rightarrow - 3\sqrt x \le 0\;\forall x \ge 0 \Rightarrow - 3\sqrt x - 9 < 0\;\forall x \ge 0\)
Mặt khác \(\sqrt x \ge 0\;\forall x \ge 0 \Rightarrow \sqrt x + 1 > 0\;\forall x \ge 0.\)
\( \Rightarrow A.B - 5 = \frac{{ - 3\sqrt x - 9}}{{\sqrt x + 1}} < 0\;\;\forall x \ge 0 \Rightarrow \,A.B < 5\)
Chọn A.
Câu hỏi 29 :
Cho biểu thức \(B = \left( {\frac{{2x + 1}}{{\sqrt {{x^3}} - 1}} - \frac{{\sqrt x }}{{x + \sqrt x + 1}}} \right).\left( {\frac{{1 + \sqrt {{x^3}} }}{{1 + \sqrt x }} - \sqrt x } \right)\) với \(x \ge 0\) và \(x \ne 1\). Tính B khi \(x = 9\)
- A \(B = 1\).
- B \(B = 2\).
- C \(B = 3\).
- D \(B = 5\).
Đáp án: B
Phương pháp giải:
+) Tìm điều kiện xác định của biểu thức.
+) Sử dụng biểu thức liên hợp.
+) Đặt nhân tử chung.
+) Rút gọn các phân thức trước khi tiến hành tính toán.
Lời giải chi tiết:
ĐKXĐ: \(x \ge 0\) và \(x \ne 1\)
\(\begin{array}{l}B = \left( {\frac{{2x + 1}}{{\sqrt {{x^3}} - 1}} - \frac{{\sqrt x }}{{x + \sqrt x + 1}}} \right).\left( {\frac{{1 + \sqrt {{x^3}} }}{{1 + \sqrt x }} - \sqrt x } \right)\\ = \frac{{2x + 1 - \sqrt x \left( {\sqrt x - 1} \right)}}{{\left( {\sqrt x - 1} \right).\left( {x + \sqrt x + 1} \right)}}.\left[ {\frac{{\left( {\sqrt x + 1} \right)\left( {x - \sqrt x + 1} \right)}}{{\sqrt x + 1}} - \sqrt x } \right]\\ = \frac{{2x + 1 - x + \sqrt x }}{{\left( {\sqrt x - 1} \right).\left( {x + \sqrt x + 1} \right)}}.\left( {1 - 2\sqrt x + x} \right)\\ = \frac{{x + \sqrt x + 1}}{{\left( {\sqrt x - 1} \right).\left( {x + \sqrt x + 1} \right)}}.{\left( {\sqrt x - 1} \right)^2} = \sqrt x - 1\end{array}\)
Ta có \(B = \sqrt x - 1\)
Với \(x = 9\) thỏa mãn điều kiện suy ra \(B = \sqrt x - 1 = \sqrt 9 - 1 = 3 - 1 = 2\).
Vậy khi \(x = 9\) thì \(B = 2\).
Câu hỏi 30 :
Cho biểu thức \(P = \left( {\frac{1}{{\sqrt x - \sqrt {x - 1} }} - \frac{{x - 3}}{{\sqrt {x - 1} - \sqrt 2 }}} \right)\left( {\frac{2}{{\sqrt 2 - \sqrt x }} - \frac{{\sqrt x + \sqrt 2 }}{{\sqrt {2x} - x}}} \right)\). Tính giá trị của P với \(x = 3 + 2\sqrt 2 \).
- A \(P = - \sqrt 5 + 1\).
- B \(P = - \sqrt 2 + 1\).
- C \(P = - \sqrt 2 + 2\).
- D \(P = - \sqrt 7 + 1\).
Đáp án: B
Phương pháp giải:
+) Tìm điều kiện xác định của biểu thức.
+) Sử dụng biểu thức liên hợp.
+) Đặt nhân tử chung.
+) Rút gọn các phân thức trước khi tiến hành tính toán.
Lời giải chi tiết:
Biểu thức P có nghĩa khi và chỉ khi : \(\left\{ \begin{array}{l}\sqrt x > 0\\\sqrt {x - 1} \ge 0\\\sqrt 2 - \sqrt x \ne 0\\\sqrt {x - 1} - \sqrt 2 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x > 0\\x \ge 1\\x \ne 2\\x \ne 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 1\\x \ne 2\\x \ne 3\end{array} \right.\)
ĐKXĐ: \(x \ge 1;x \ne 2;x \ne 3\)
\(\begin{array}{l}P = \left( {\frac{1}{{\sqrt x - \sqrt {x - 1} }} - \frac{{x - 3}}{{\sqrt {x - 1} - \sqrt 2 }}} \right)\left( {\frac{2}{{\sqrt 2 - \sqrt x }} - \frac{{\sqrt x + \sqrt 2 }}{{\sqrt {2x} - x}}} \right)\\P = \left[ {\frac{{\left( {\sqrt x + \sqrt {x - 1} } \right)}}{{\left( {\sqrt x - \sqrt {x - 1} } \right)\left( {\sqrt x + \sqrt {x - 1} } \right)}} - \frac{{\left( {x - 3} \right)\left( {\sqrt {x - 1} + \sqrt 2 } \right)}}{{\left( {\sqrt {x - 1} - \sqrt 2 } \right)\left( {\sqrt {x - 1} + \sqrt 2 } \right)}}} \right]\left[ {\frac{2}{{\sqrt 2 - \sqrt x }} - \frac{{\sqrt x + \sqrt 2 }}{{\sqrt x \left( {\sqrt 2 - \sqrt x } \right)}}} \right]\\P = \left[ {\frac{{\sqrt x + \sqrt {x - 1} }}{{x - \left( {x - 1} \right)}} - \frac{{\left( {x - 3} \right)\left( {\sqrt {x - 1} + \sqrt 2 } \right)}}{{\left( {x - 1} \right) - 2}}} \right].\frac{{2\sqrt x - \sqrt x - \sqrt 2 }}{{\sqrt x \left( {\sqrt 2 - \sqrt x } \right)}}\\P = \left( {\frac{{\sqrt x + \sqrt {x - 1} }}{{x - x + 1}} - \frac{{\left( {x - 3} \right)\left( {\sqrt {x - 1} + \sqrt 2 } \right)}}{{x - 3}}} \right).\frac{{ - \left( {\sqrt 2 - \sqrt x } \right)}}{{\sqrt x \left( {\sqrt 2 - \sqrt x } \right)}}\\P = \left( {\sqrt x + \sqrt {x - 1} - \sqrt {x - 1} - \sqrt 2 } \right).\frac{{ - 1}}{{\sqrt x }} = \frac{{\left( {\sqrt x - \sqrt 2 } \right).\left( { - 1} \right)}}{{\sqrt x }} = \frac{{\sqrt 2 - \sqrt x }}{{\sqrt x }}\end{array}\)
Ta có: \(x = 3 + 2\sqrt 2 = {\left( {\sqrt 2 + 1} \right)^2} \Rightarrow \sqrt x = \sqrt {{{\left( {\sqrt 2 + 1} \right)}^2}} = \left| {\sqrt 2 + 1} \right| = \sqrt 2 + 1\,\,\left( {Do\,\,\sqrt 2 + 1 > 0} \right)\)
Thay \(\sqrt x = \sqrt 2 + 1\) vào biểu thức \(P = \frac{{\sqrt 2 - \sqrt x }}{{\sqrt x }}\), ta có: \(P = \frac{{\sqrt 2 - \sqrt 2 - 1}}{{\sqrt 2 + 1}} = \frac{{ - 1}}{{\sqrt 2 + 1}} = - \sqrt 2 + 1\).
Vậy khi \(x = 3 + 2\sqrt 2 \) thì \(P = - \sqrt 2 + 1\).
Câu hỏi 31 :
Cho biểu thức \(P = \left( {\frac{{1 - a\sqrt a }}{{1 - \sqrt a }} + \sqrt a } \right).\left( {\frac{{1 + a\sqrt a }}{{1 + \sqrt a }} - \sqrt a } \right)\) .Tính \(a\) để \(P < 7 - 4\sqrt 3 \)
- A \(a \in \left( {\sqrt 3 - 1;3 - \sqrt 3 } \right)/\left\{ 1 \right\}\).
- B \(a \in \left( {\sqrt 2 - 1;3 - \sqrt 3 } \right)/\left\{ 1 \right\}\).
- C \(a \in \left( {\sqrt 3 - 1;3 - \sqrt 7 } \right)/\left\{ 1 \right\}\).
- D \(a \in \left( {\sqrt 3 - 1;7 - \sqrt 3 } \right)/\left\{ 1 \right\}\).
Đáp án: A
Phương pháp giải:
+) Bước 1: Tìm điều kiện xác định của P
+) Bước 2: Áp dụng hằng đẳng thức rồi rút gọn P.
+) Bước 3: Cho \(P < 7 - 4\sqrt 3 \) ( P đã rút gọn ở trên). Từ đó tìm giá trị của a thỏa mãn yêu cầu.
Lời giải chi tiết:
ĐKXĐ: \(\left\{ \begin{array}{l}a \ge 0\\1 - \sqrt a \ne 0\end{array} \right. \Leftrightarrow a \ge 0,a \ne 1\)
\(\begin{array}{l}P = \left( {\frac{{1 - a\sqrt a }}{{1 - \sqrt a }} + \sqrt a } \right).\left( {\frac{{1 + a\sqrt a }}{{1 + \sqrt a }} - \sqrt a } \right)\\P = \left( {\frac{{\left( {1 - \sqrt a } \right).\left( {1 + \sqrt a + a} \right)}}{{1 - \sqrt a }} + \sqrt a } \right).\left( {\frac{{\left( {1 + \sqrt a } \right).\left( {1 - \sqrt a + a} \right)}}{{1 + \sqrt a }} - \sqrt a } \right)\\P = \left( {1 + \sqrt a + a + \sqrt a } \right).\left( {1 - \sqrt a + a - \sqrt a } \right) = {\left( {1 + \sqrt a } \right)^2}.{\left( {1 - \sqrt a } \right)^2} = {\left( {1 - a} \right)^2}\\P < 7 - 4\sqrt 3 \Leftrightarrow P < {\left( {2 - \sqrt 3 } \right)^2}\\ \Rightarrow {\left( {1 - a} \right)^2} < {\left( {2 - \sqrt 3 } \right)^2} \Leftrightarrow \left| {1 - a} \right| < \left| {2 - \sqrt 3 } \right| \Leftrightarrow \left| {a - 1} \right| < 2 - \sqrt 3 \\ \Leftrightarrow - 2 + \sqrt 3 < 1 - a < 2 - \sqrt 3 \Leftrightarrow \sqrt 3 - 1 < a < 3 - \sqrt 3 \end{array}\)
Kết hợp với điều kiện ta được \(a \in \left( {\sqrt 3 - 1;3 - \sqrt 3 } \right)/\left\{ 1 \right\}\) .
Vậy \(a \in \left( {\sqrt 3 - 1;3 - \sqrt 3 } \right)/\left\{ 1 \right\}\).
Câu hỏi 32 :
Cho biểu thức \(P = \left( {\frac{{\sqrt x + 1}}{{\sqrt x - 1}} - \frac{{\sqrt x - 1}}{{\sqrt x + 1}}} \right):\left( {\frac{1}{{\sqrt x + 1}} - \frac{{\sqrt x }}{{1 - \sqrt x }} + \frac{2}{{x - 1}}} \right)\)
a) Tính giá trị của P khi \(x = \frac{{\sqrt {7 - 4\sqrt 3 } }}{2}\). b) Tính các giá trị của x để \(P = \frac{1}{2}\).
- A a)\(P = 20 - 12\sqrt 5 \).
b)\(x = 17 + 12\sqrt 2 \)hoặc \(x = 17 - 12\sqrt 2 \)
- B a)\(P = 22 - 12\sqrt 3 \).
b)\(x = 17 + 12\sqrt 2 \)hoặc \(x = 17 - 12\sqrt 2 \)
- C a)\(P = 20 - 12\sqrt 3 \).
b)\(x = 17 + 12\sqrt 2 \)hoặc \(x = 17 - 12\sqrt 2 \)
- D a)\(P = 20 - 12\sqrt 3 \).
b)\(x = 47 + 12\sqrt 2 \)hoặc \(x = 17 - 12\sqrt 2 \)
Đáp án: C
Phương pháp giải:
- Sử dụng biểu thức liên hợp.
- Rút gọn biểu thức.
Lời giải chi tiết:
ĐKXĐ: \(\left\{ \begin{array}{l}x \ge 0\\x \ne 1\end{array} \right.\)
\(\begin{array}{l}P = \left( {\frac{{\left( {\sqrt x + 1} \right)\left( {\sqrt x + 1} \right) - \left( {\sqrt x - 1} \right)\left( {\sqrt x - 1} \right)}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}} \right):\left( {\frac{{\sqrt x - 1 + \sqrt x \left( {\sqrt x + 1} \right) + 2}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}} \right)\\\,\,\,\,\, = \left( {\frac{{{{\left( {\sqrt x + 1} \right)}^2} - {{\left( {\sqrt x - 1} \right)}^2}}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}} \right).\left( {\frac{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}{{x + 2\sqrt x + 1}}} \right)\\\,\,\,\,\, = \frac{{\left( {\sqrt x + 1 - \sqrt x + 1} \right)\left( {\sqrt x + 1 + \sqrt x - 1} \right)}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}.\frac{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}{{{{\left( {\sqrt x + 1} \right)}^2}}}\\\,\,\,\,\, = \frac{{4\sqrt x }}{{{{\left( {\sqrt x + 1} \right)}^2}}}\end{array}\)
Vậy \(P = \frac{{4\sqrt x }}{{{{\left( {\sqrt x + 1} \right)}^2}}}\) (1)
a) Ta có \(x = \frac{{\sqrt {7 - 4\sqrt 3 } }}{2} = \frac{{\sqrt {{2^2} - 2.2.\sqrt 3 + {{\left( {\sqrt 3 } \right)}^2}} }}{2} = \frac{{\sqrt {{{\left( {2 - \sqrt 3 } \right)}^2}} }}{2} = \frac{{\left| {2 - \sqrt 3 } \right|}}{2} = \frac{{2 - \sqrt 3 }}{2}\,\,\left( {Do\,\,2 - \sqrt 3 > 0} \right)\)
\( \Rightarrow \sqrt x = \sqrt {\frac{{2 - \sqrt 3 }}{2}} = \frac{{\sqrt {4 - 2\sqrt 3 } }}{2} = \frac{{\sqrt {{{\left( {\sqrt 3 - 1} \right)}^2}} }}{2} = \frac{{\left| {\sqrt 3 - 1} \right|}}{2} = \frac{{\sqrt 3 - 1}}{2}\,\,\left( {Do\,\,\sqrt 3 - 1 > 0} \right)\)
Thay \(\sqrt x = \frac{{\sqrt 3 - 1}}{2}\) vào biểu thức P ta được:
\(P = \frac{{4\left( {\frac{{\sqrt 3 - 1}}{2}} \right)}}{{{{\left( {\frac{{\sqrt 3 - 1}}{2} + 1} \right)}^2}}} = \frac{{8\left( {\sqrt 3 - 1} \right)}}{{{{\left( {\sqrt 3 + 1} \right)}^2}}} = \frac{{8\left( {\sqrt 3 - 1} \right)}}{{4 + 2\sqrt 3 }} = \frac{{4\left( {\sqrt 3 - 1} \right)}}{{2 + \sqrt 3 }} = 4\left( {\sqrt 3 - 1} \right)\left( {2 - \sqrt 3 } \right) = - 20 + 12\sqrt 3 \)
Vậy khi \(x = \frac{{\sqrt {7 - 4\sqrt 3 } }}{2}\) thì \(P = 20 - 12\sqrt 3 \).
b) Theo bài ra ta có \(P = \frac{1}{2} \Leftrightarrow \frac{{4\sqrt x }}{{{{\left( {\sqrt x + 1} \right)}^2}}} = \frac{1}{2}\)
\(\begin{array}{l} \Leftrightarrow x + 2\sqrt x + 1 = 8\sqrt x \Leftrightarrow x - 6\sqrt x + 1 = 0\\ \Leftrightarrow \left[ \begin{array}{l}\sqrt x = 3 + 2\sqrt 2 \\\sqrt x = 3 - 2\sqrt 2 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 17 + 12\sqrt 2 \\x = 17 - 12\sqrt 2 \end{array} \right.\,\,\left( {tm} \right)\end{array}\)
Vậy với \(x = 17 + 12\sqrt 2 \)hoặc \(x = 17 - 12\sqrt 2 \) thì \(P = \frac{1}{2}\).
Câu hỏi 33 :
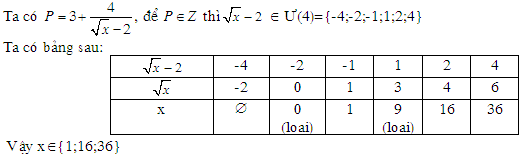
Cho \(A = \left( {1 - \dfrac{{\sqrt x }}{{1 + \sqrt x }}} \right):\left( {\dfrac{{\sqrt x + 3}}{{\sqrt x - 2}} + \dfrac{{\sqrt x + 2}}{{3 - \sqrt x }} + \dfrac{{\sqrt x + 2}}{{x - 5\sqrt x + 6}}} \right)\) với \(x \ge 0,x \ne 4,x \ne 9.\)
a) Rút gọn A.
b) Tìm \(x \in Z\) để \(A \in Z\)
c) Tìm x để \(A < 0.\)
- A \(\begin{array}{l}
a)\,\,A = \dfrac{{\sqrt x - 2}}{{\sqrt x + 1}}\\
b)\,\,x \in \left\{ {0} \right\}\\
c)\,\,0 \le x < 4
\end{array}\) - B \(\begin{array}{l}
a)\,\,A = \dfrac{{\sqrt x - 2}}{{\sqrt x + 1}}\\
b)\,\,x \in \left\{ {0;4} \right\}\\
c)\,\,0 < x < 4
\end{array}\) - C \(\begin{array}{l}
a)\,\,A = \dfrac{3}{{\sqrt x + 1}}\\
b)\,\,x \in \left\{ {0;4} \right\}\\
c)\,\,0 \le x < 4
\end{array}\) - D \(\begin{array}{l}
a)\,\,A = \dfrac{{\sqrt x - 2}}{{\sqrt x + 1}}\\
b)\,\,x \in \left\{ {0; \pm 4} \right\}\\
c)\,\,0 \le x < 4
\end{array}\)
Đáp án: A
Phương pháp giải:
a) Quy đồng, rút gọn.
b) Đưa biểu thức về dạng \(A\left( x \right) + \dfrac{C}{{B\left( x \right)}}\) với C là hằng số. Để biểu thức đó là số nguyên thì \(B\left( x \right) \in U\left( C \right)\).
c) Nhận xét mẫu số trước khi giải bất phương trình, lưu ý kết hợp điều kiện.
Lời giải chi tiết:
a) Với \(x \ge 0,x \ne 4,x \ne 9.\) Ta có:
\(\begin{array}{l}A = \left( {1 - \dfrac{{\sqrt x }}{{1 + \sqrt x }}} \right):\left( {\dfrac{{\sqrt x + 3}}{{\sqrt x - 2}} + \dfrac{{\sqrt x + 2}}{{3 - \sqrt x }} + \dfrac{{\sqrt x + 2}}{{x - 5\sqrt x + 6}}} \right)\\A = \dfrac{1}{{\sqrt x + 1}}:\left( {\dfrac{{\left( {\sqrt x + 3} \right)\left( {\sqrt x - 3} \right)}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x - 3} \right)}} - \dfrac{{\left( {\sqrt x + 2} \right)\left( {\sqrt x - 2} \right)}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x - 3} \right)}} + \dfrac{{\sqrt x + 2}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x - 3} \right)}}} \right)\\A = \dfrac{1}{{\sqrt x + 1}}:\dfrac{{x - 9 - \left( {x - 4} \right) + \sqrt x + 2}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x - 3} \right)}}\\A = \dfrac{1}{{\sqrt x + 1}}:\dfrac{{\sqrt x - 3}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x - 3} \right)}} = \dfrac{{\sqrt x - 2}}{{\sqrt x + 1}}.\end{array}\)
b) \(A = \dfrac{{\sqrt x - 2}}{{\sqrt x + 1}} = 1 - \dfrac{3}{{\sqrt x + 1}}\left( {x \ge 0} \right)\)
Để \(A \in Z\) với x nguyên thì \(\sqrt x + 1\) là ước nguyên dương của 3 do \(\sqrt x + 1 > 0\)
.\( \Rightarrow \left[ \begin{array}{l}\sqrt x + 1 = 1 \Leftrightarrow x = 0\,\,\,\left( {tm} \right)\\\sqrt x + 1 = 3 \Leftrightarrow x = 4\,\,\left( {ktm} \right)\end{array} \right.\)
Vậy với \(x = 0\) thì \(A \in Z\)
c) \(A < 0 \Leftrightarrow \dfrac{{\sqrt x - 2}}{{\sqrt x + 1}} < 0.\)
Do \(\sqrt x + 1 > 0 \Rightarrow \dfrac{{\sqrt x - 2}}{{\sqrt x + 1}} < 0 \Leftrightarrow \sqrt x - 2 < 0 \Leftrightarrow x < 4.\)
Kết với \(x \ge 0\), suy ra \(A > 0 < = > 0 \le x < 4.\)
Vậy \(0 \le x < 4\) thì \(A < 0.\)
Câu hỏi 34 :
Cho biểu thức \(Q = \left( {\dfrac{1}{{\sqrt x - 1}} + \dfrac{2}{{x - 1}}} \right):\left( {\dfrac{{x + \sqrt x }}{{\sqrt x + 1}} - \dfrac{{1 - \sqrt x }}{{\sqrt x - x}}} \right)\) với \(x > 0\), \(x \ne 1\) .
a) Rút gọn biểu thức Q.
b) Tìm các giá trị của x để \(Q = - 1\)
- A \(\begin{array}{l}
a)\,\,Q = \frac{{\sqrt x \left( {\sqrt x + 3} \right)}}{{{{\left( {x - 1} \right)}^2}}}\\
b)\,\,x = 2
\end{array}\) - B \(\begin{array}{l}
a)\,\,Q = \dfrac{{\sqrt x + 3}}{{{{\left( {x - 1} \right)}^2}}}\\
b)\,\,x \in \emptyset
\end{array}\) - C \(\begin{array}{l}
a)\,\,Q = \dfrac{{\sqrt x \left( {\sqrt x + 3} \right)}}{{{{\left( {x - 1} \right)}^2}}}\\
b)\,\,x \in \emptyset
\end{array}\) - D \(\begin{array}{l}
a)\,\,Q = \dfrac{{\sqrt x \left( {\sqrt x + 3} \right)}}{{{{\left( {x - 1} \right)}^2}}}\\
b)\,\,x \in R
\end{array}\)
Đáp án: C
Phương pháp giải:
- Nhân liên hợp
- Quy đồng mẫu số
- Giải và biện luận phương trình
Lời giải chi tiết:
a) Ta có \(Q = \left( {\dfrac{1}{{\sqrt x - 1}} + \dfrac{2}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}} \right):\left( {\dfrac{{\sqrt x \left( {\sqrt x + 1} \right)}}{{\sqrt x + 1}} - \dfrac{{1 - \sqrt x }}{{\sqrt x \left( {1 - \sqrt x } \right)}}} \right)\)
\(\begin{array}{l} = \dfrac{{\left( {\sqrt x + 1} \right) + 2}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}:\left( {\sqrt x - \dfrac{1}{{\sqrt x }}} \right)\\ = \dfrac{{\sqrt x + 3}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}:\dfrac{{x - 1}}{{\sqrt x }}\\ = \dfrac{{\sqrt x + 3}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}.\dfrac{{\sqrt x }}{{x - 1}}\\ = \dfrac{{\sqrt x \left( {\sqrt x + 3} \right)}}{{{{\left( {x - 1} \right)}^2}.}}\end{array}\)
Vậy \(Q = \dfrac{{\sqrt x \left( {\sqrt x + 3} \right)}}{{{{\left( {x - 1} \right)}^2}}}\)
b. Ta thấy biểu thức \(Q = \dfrac{{\sqrt x \left( {\sqrt x + 3} \right)}}{{{{\left( {x - 1} \right)}^2}}}\) luôn lớn hơn 0 với \(\forall x > 0,x \ne 1\)
\( \Rightarrow \)\(Q = \dfrac{{\sqrt x \left( {\sqrt x + 3} \right)}}{{{{\left( {x - 1} \right)}^2}}} = - 1\) (vô lý)
Vậy không tồn tại giá trị nào của x để \(Q = \dfrac{{\sqrt x \left( {\sqrt x + 3} \right)}}{{{{\left( {x - 1} \right)}^2}}} = - 1.\)
Câu hỏi 35 :
Cho biểu thức \(P = \left( {1 - \dfrac{{x - 3\sqrt x }}{{x - 9}}} \right):\left( {\dfrac{{\sqrt x - 3}}{{2 - \sqrt x }} + \dfrac{{\sqrt x - 2}}{{3 + \sqrt x }} - \dfrac{{9 - x}}{{x + \sqrt x - 6}}} \right)\) với \(x \ge 0,\)\(x \ne 9\), \(x \ne 4\).
a) Rút gọc biểu thức P b) Tìm các giá trị của x để \(P = 1\).
- A \(\begin{array}{l}
a)\,\,P = \sqrt x - 2\\
b)\,\,x = 25
\end{array}\) - B \(\begin{array}{l}
a)\,\,P = \dfrac{1}{{\sqrt x - 2}}\\
b)\,\,x = 25
\end{array}\) - C \(\begin{array}{l}
a)\,\,P = \dfrac{3}{{\sqrt x - 2}}\\
b)\,\,x = 5
\end{array}\) - D \(\begin{array}{l}
a)\,\,P = \dfrac{3}{{\sqrt x - 2}}\\
b)\,\,x = 25
\end{array}\)
Đáp án: D
Phương pháp giải:
a) Sử dụng hằng đẳng thức, quy đồng, rút gọn biểu thức.
b) Giải phương trình \(P = 1\) , lưu ý ĐKXĐ.
Lời giải chi tiết:
a) Ta có
\(\begin{array}{l}P = \left( {1 - \dfrac{{\sqrt x \left( {\sqrt x - 3} \right)}}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}}} \right):\left( {\dfrac{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right) + \left( {\sqrt x - 2} \right)\left( {2 - \sqrt x } \right)}}{{\left( {2 - \sqrt x } \right)\left( {3 + \sqrt x } \right)}} - \dfrac{{9 - x}}{{x + \sqrt x - 6}}} \right)\\P = \left( {1 - \dfrac{{\sqrt x }}{{\sqrt x + 3}}} \right):\left( {\dfrac{{x - 9 - {{\left( {\sqrt x - 2} \right)}^2}}}{{6 - \sqrt x - x}} - \dfrac{{9 - x}}{{x + \sqrt x - 6}}} \right)\\P = \dfrac{{\sqrt x + 3 - \sqrt x }}{{\sqrt x + 3}}:\left( {\dfrac{{x - 9 - \left( {x - 4\sqrt x + 4} \right)}}{{6 - \sqrt x - x}} - \dfrac{{9 - x}}{{x + \sqrt x - 6}}} \right)\\P = \dfrac{3}{{\sqrt x + 3}}:\left( {\dfrac{{13 - 4\sqrt x }}{{x + \sqrt x - 6}} - \dfrac{{9 - x}}{{x + \sqrt x - 6}}} \right)\\P = \dfrac{3}{{\sqrt x + 3}}:\dfrac{{13 - 4\sqrt x - 9 + x}}{{x + \sqrt x - 6}}\\P = \dfrac{3}{{\sqrt x + 3}}.\dfrac{{\left( {\sqrt x + 3} \right)\left( {\sqrt x - 2} \right)}}{{x - 4\sqrt x + 4}}\\P = \dfrac{{3\left( {\sqrt x - 2} \right)}}{{{{\left( {\sqrt x - 2} \right)}^2}}} = \dfrac{3}{{\sqrt x - 2}}\end{array}\)
b) Để \(P = 1 \Leftrightarrow \dfrac{3}{{\sqrt x - 2}} = 1 \Leftrightarrow 3 = \sqrt x - 2 \Leftrightarrow \sqrt x = 5 \Leftrightarrow x = 25\,\,\left( {tm} \right)\)
Vậy với \(x = 25\) thì ta có giá trị của \(P = 1\)
Câu hỏi 36 :
Cho biểu thức \(P = \left( {\frac{{x - 6}}{{x + 3\sqrt x }} - \frac{1}{{\sqrt x }} + \frac{1}{{\sqrt x + 3}}} \right):\frac{{2\sqrt x - 6}}{{x + 1}}\) với \(x > 0,\;\;x \ne 9.\)
Câu 1: Rút gọn biểu thức P.
- A \(P = \frac{{x + 1}}{{2\sqrt x }}\)
- B \(P = \frac{{x + 1}}{{x - 9}}\)
- C \(P = \frac{{x + 1}}{{\sqrt x - 3}}\)
- D \(P = \frac{{\sqrt x + 3}}{{2\sqrt x }}\)
Đáp án: A
Phương pháp giải:
Quy đồng mẫu các phân thức sau đó biến đổi và rút gọn biểu thức P.
Lời giải chi tiết:
Điều kiện: \(x > 0,\;x \ne 9.\)
\(\begin{array}{l}P = \left( {\frac{{x - 6}}{{x + 3\sqrt x }} - \frac{1}{{\sqrt x }} + \frac{1}{{\sqrt x + 3}}} \right):\frac{{2\sqrt x - 6}}{{x + 1}}\; = \left( {\frac{{x - 6}}{{\sqrt x \left( {\sqrt x + 3} \right)}} - \frac{1}{{\sqrt x }} + \frac{1}{{\sqrt x + 3}}} \right):\frac{{2\left( {\sqrt x - 3} \right)}}{{x + 1}}\\\;\;\; = \frac{{x - 6 - \left( {\sqrt x + 3} \right) + \sqrt x }}{{\sqrt x \left( {\sqrt x + 3} \right)}}.\frac{{x + 1}}{{2\left( {\sqrt x - 3} \right)}}\; = \frac{{x - 6 - \sqrt x - 3 + \sqrt x }}{{\sqrt x \left( {\sqrt x + 3} \right)}}.\frac{{x + 1}}{{2\left( {\sqrt x - 3} \right)}}\\\;\;\; = \frac{{\left( {x - 9} \right)\left( {x + 1} \right)}}{{2\sqrt x \left( {x - 9} \right)}} = \frac{{x + 1}}{{2\sqrt x }}.\end{array}\)
Chọn A.
Câu 2: Tìm giá trị của x để \(P = 1.\)
- A \(x = 16\)
- B \(x = 4\)
- C \(x = 2\)
- D \(x = 1\)
Đáp án: D
Phương pháp giải:
Lấy kết quả của biểu thức P đã rút gọn ở trên. Giải phương trình \(P = 1\) sau đó đối chiếu với điều kiện của x rồi kết luận.
Lời giải chi tiết:
Điều kiện: \(x > 0,\;x \ne 9.\)
\(\begin{array}{l}P = 1 \Leftrightarrow \frac{{x + 1}}{{2\sqrt x }} = 1 \Leftrightarrow x + 1 = 2\sqrt x \Leftrightarrow x - 2\sqrt x + 1 = 0\\ \Leftrightarrow {\left( {\sqrt x - 1} \right)^2} = 0 \Leftrightarrow \sqrt x - 1 = 0 \Leftrightarrow \sqrt x = 1 \Leftrightarrow x = 1\;\;\left( {tm} \right).\end{array}\)
Vậy \(x = 1\) thì \(P = 1.\)
Chọn D.
Câu hỏi 37 :
Rút gọn \(M = \frac{{x{z^2}}}{{4xy}}.\frac{{20{x^2}}}{{{z^3}}}\) với \(\left( {xyz \ne 0} \right)\) ta được
- A \(M = \frac{{5x}}{{y{z^2}}}\)
- B \(M = \frac{{5zx}}{y}\)
- C \(M = \frac{{5{x^2}}}{{yz}}\)
- D \(M = \frac{{5{x^3}}}{{y{z^2}}}\)
Đáp án: C
Phương pháp giải:
Rút gọn những đơn thức đồng dạng.
Lời giải chi tiết:
\(M = \frac{{x{z^2}}}{{4xy}}.\frac{{20{x^2}}}{{{z^3}}} = \frac{{20{x^3}{z^2}}}{{4xy{z^3}}} = \frac{{5{x^2}}}{{yz}}\).
Chọn C.
Câu hỏi 38 :
Với \(x < 0\) hãy rút gọn biểu thức \(N = \sqrt {{x^2}} + \sqrt[3]{{{x^3}}}\)
- A \(N = 2x\)
- B \(N = 0\)
- C \(N = x\)
- D \(N = - 2x\)
Đáp án: B
Phương pháp giải:
Áp dụng công thức: \(\sqrt {{A^2}} = \left[ \begin{array}{l}A\,\,\,khi\,\,\,\,A\,\,\, \ge 0\\ - A\,\,\,\,khi\,\,\,\,A < 0\end{array} \right..\)
Lời giải chi tiết:
Với \(x < 0\) thì \(N = \sqrt {{x^2}} + \sqrt[3]{{{x^3}}} = \left| x \right| + x = - x + x = 0.\)
Chọn B
Câu hỏi 39 :
Chứng minh rằng : \(\frac{{ab}}{{\left( {c + a} \right)\left( {c + b} \right)}} + \frac{{ac}}{{\left( {b + c} \right)\left( {b + a} \right)}} + \frac{{bc}}{{\left( {a + b} \right)\left( {a + c} \right)}} + \frac{{2abc}}{{\left( {a + b} \right)\left( {a + c} \right)\left( {b + c} \right)}} = 1\)
Phương pháp giải:
Sử dụng định lí: Nếu đa thức : \(f\left( x \right) = ax + b\) có ít nhất 2 nghiệm thì \(a = b = 0\) tức là \(f\left( x \right) = 0\) với mọi x.
Lời giải chi tiết:
Đặt
\(\begin{array}{l}P(x) = \frac{{xb}}{{\left( {c + x} \right)\left( {c + b} \right)}} + \frac{{xc}}{{\left( {b + c} \right)\left( {b + x} \right)}} + \frac{{bc}}{{\left( {x + b} \right)\left( {x + c} \right)}} + \frac{{2xbc}}{{\left( {x + b} \right)\left( {x + c} \right)\left( {b + c} \right)}} - 1\\\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{xb\left( {x + b} \right) + xc\left( {x + c} \right) + bc\left( {b + c} \right) + 2xbc - \left( {x + b} \right)\left( {x + c} \right)\left( {b + c} \right)}}{{\left( {x + b} \right)\left( {x + c} \right)\left( {b + c} \right)}}\end{array}\)
Xét tử số \(f\left( x \right) = xb\left( {x + b} \right) + xc\left( {x + c} \right) + bc\left( {b + c} \right) + 2xbc - \left( {x + b} \right)\left( {x + c} \right)\left( {b + c} \right)\) có hệ số của \({x^2}\) là \(b + c - \left( {b + c} \right) = 0\) \( \Rightarrow \) Bậc của \(f\left( x \right)\) nhỏ hơn hoặc bằng 1.
Ta có : \(\left\{ \begin{array}{l}f\left( b \right) = {b^2}.2b + bc\left( {b + c} \right) + bc\left( {b + c} \right) + 2{b^2}c - 2b.{\left( {b + c} \right)^2} = 0\\f\left( c \right) = cb\left( {c + b} \right) + 2{c^3} + bc\left( {b + c} \right) + 2b{c^2} - 2c\left( {c + b} \right)\left( {b + c} \right) = 0\end{array} \right.\)
Do đó b, c là 2 nghiệm của phương trình \(f\left( x \right) = 0\).
Bậc của \(f\left( x \right)\) nhỏ hơn hoặc bằng 1, trong khi đó phương trình \(f\left( x \right) = 0\) lại có 2 nghiệm phân biệt \( \Leftrightarrow f\left( x \right) \equiv 0\,\,\forall x\) hay \(P\left( x \right) = 0\,\,\forall x\).
\(\begin{array}{l}P\left( x \right) = \frac{{xb}}{{\left( {c + x} \right)\left( {c + b} \right)}} + \frac{{xc}}{{\left( {b + c} \right)\left( {b + x} \right)}} + \frac{{bc}}{{\left( {x + b} \right)\left( {x + c} \right)}} + \frac{{2xbc}}{{\left( {x + b} \right)\left( {x + c} \right)\left( {b + c} \right)}} - 1\\P\left( x \right) = \frac{{xb\left( {x + b} \right) + xc\left( {x + c} \right) + bc\left( {b + c} \right) + 2xbc - \left( {x + b} \right)\left( {x + c} \right)\left( {b + c} \right)}}{{\left( {x + b} \right)\left( {x + c} \right)\left( {b + c} \right)}} = 0\\ \Rightarrow P\left( a \right) = \frac{{ab}}{{\left( {c + a} \right)\left( {c + b} \right)}} + \frac{{ac}}{{\left( {b + c} \right)\left( {b + a} \right)}} + \frac{{bc}}{{\left( {a + b} \right)\left( {a + c} \right)}} + \frac{{2abc}}{{\left( {a + b} \right)\left( {a + c} \right)\left( {b + c} \right)}} - 1 = 0\\ \Leftrightarrow \frac{{ab}}{{\left( {c + a} \right)\left( {c + b} \right)}} + \frac{{ac}}{{\left( {b + c} \right)\left( {b + a} \right)}} + \frac{{bc}}{{\left( {a + b} \right)\left( {a + c} \right)}} + \frac{{2abc}}{{\left( {a + b} \right)\left( {a + c} \right)\left( {b + c} \right)}} = 1\end{array}\)
Vậy \(\frac{{ab}}{{\left( {c + a} \right)\left( {c + b} \right)}} + \frac{{ac}}{{\left( {b + c} \right)\left( {b + a} \right)}} + \frac{{bc}}{{\left( {a + b} \right)\left( {a + c} \right)}} + \frac{{2abc}}{{\left( {a + b} \right)\left( {a + c} \right)\left( {b + c} \right)}} = 1\)
Câu hỏi 40 :
Tính giá trị của A= \(\frac{1}{{2\sqrt 1 + 1\sqrt 2 }} + \frac{1}{{3\sqrt 2 + 2\sqrt 3 }} + ... + \frac{1}{{2018\sqrt {2017} + 2017\sqrt {2018} }}\)
- A \(A=1-\frac{2}{\sqrt{2018}}\)
- B \(A=1-\frac{1}{\sqrt{2028}}\)
- C \(A=1-\frac{1}{\sqrt{2015}}\)
- D \(A=1-\frac{1}{\sqrt{2018}}\)
Đáp án: D
Phương pháp giải:
\(\frac{1}{{k\sqrt {k - 1} + \left( {k - 1} \right)\sqrt k }} = \frac{1}{{\sqrt {k - 1} }} - \frac{1}{{\sqrt k }}\)
Lời giải chi tiết:
Ta có: \(k\sqrt {k - 1} + \left( {k - 1} \right)\sqrt k \, = \sqrt {k\left( {k - 1} \right)} \left( {\sqrt k + \sqrt {k - 1} } \right)\) với \(k \ge 1\).
\(\begin{array}{l} \Rightarrow \frac{1}{{k\sqrt {k - 1} + \left( {k - 1} \right)\sqrt k }} = \frac{1}{{\sqrt {k\left( {k - 1} \right)} \left( {\sqrt k + \sqrt {k - 1} } \right)}} = \frac{{\left( {\sqrt k - \sqrt {k - 1} } \right)}}{{\sqrt {k\left( {k - 1} \right)} \left( {\sqrt k + \sqrt {k - 1} } \right)\left( {\sqrt k - \sqrt {k - 1} } \right)}}\\ = \frac{{\sqrt k - \sqrt {k - 1} }}{{\sqrt {k\left( {k - 1} \right)} }} = \frac{{\sqrt k - \sqrt {k - 1} }}{{\sqrt k .\sqrt {k - 1} }} = \frac{1}{{\sqrt {k - 1} }} - \frac{1}{{\sqrt k }}\end{array}\)
Thay lại vào A ta được:
\(\begin{array}{l}A = \frac{1}{{2\sqrt 1 + 1\sqrt 2 }} + \frac{1}{{3\sqrt 2 + 2\sqrt 3 }} + ... + \frac{1}{{2018\sqrt {2017} + 2017\sqrt {2018} }}\\\,\,\,\,\, = \,\left( {\frac{1}{{\sqrt 1 }} - \frac{1}{{\sqrt 2 }}} \right) + \left( {\frac{1}{{\sqrt 2 }} - \frac{1}{{\sqrt 3 }}} \right) + ..... + \left( {\frac{1}{{\sqrt {2017} }} - \frac{1}{{\sqrt {2018} }}} \right)\\\,\,\,\,\, = 1 - \frac{1}{{\sqrt {2018} }}\end{array}\)
>> Học trực tuyến lớp 9 và Lộ trình UP10 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Lộ trình học tập 3 giai đoạn: Học nền tảng lớp 9, Ôn thi vào lớp 10, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
 |
 |
 |
 |
 |
 |
Các bài khác cùng chuyên mục