40 bài tập vận dụng ôn tập chương 1: Hệ thức lượng trong tam giác vuông
Làm đề thiCâu hỏi 1 :
Cho tam giác \(MNP\) vuông ở \(M,\,MN = 4a;\) \(MP = 3a.\) Khi đó, \(\tan P\) bằng
- A \(\frac{3}{4}.\)
- B \(\frac{4}{3}.\)
- C \(\frac{3}{5}.\)
- D \(\frac{4}{5}.\)
Đáp án: B
Phương pháp giải:
Sử dụng tỉ số lượng giác của góc nhọn
Lời giải chi tiết:
Xét tam giác \(MNP\) vuông tại \(M,\) theo định nghĩa tỉ số lượng giác của góc nhọn ta có:
\(\tan P = \frac{{MN}}{{MP}} = \frac{{4a}}{{3a}} = \frac{4}{3}.\)
Chọn B
Câu hỏi 2 :
Cho hình thang cân \(ABCD\,\,\,\left( {AB\parallel CD} \right);\) \(CD = 2AD = 2AB = 8\). Tính diện tích của hình thang đó.
- A \(12\sqrt 2 \)
- B \(12\sqrt 3 \)
- C \(12\)
- D \(12\sqrt 6 \)
Đáp án: B
Phương pháp giải:
- Kẻ \(AH,\,\,BK\) cùng vuông góc với \(CD\) \(\left( {H,\,\,K \in CD} \right)\). Chứng minh \(ABKH\) là hình chữ nhật.
- Tính \(DH,\,\,CK\).
- Áp dụng định lí Pytago tính \(AH\).
- Tính diện tích hình thang: \({S_{ABCD}} = \dfrac{{\left( {AB + CD} \right).AH}}{2}\).
Lời giải chi tiết:
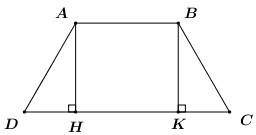
Kẻ \(AH,\,\,BK\) cùng vuông góc với \(CD\) \(\left( {H,\,\,K \in CD} \right)\).
Xét tứ giác \(ABKH\) có: \(\left\{ \begin{array}{l}AB\parallel HK\\AH\parallel BK\end{array} \right.\), suy ra \(ABKH\) là hình bình hành.
Lại có \(\angle AHK = {90^0}\) nên \(ABKH\) là hình chữ nhật, do đó \(HK = AB = 4\).
Xét \(\Delta ADH\) và \(\Delta BCK\) có:
\(\angle AHD = \angle BKC = {90^0}\);
\(AD = BC\) (tính chất hình thang cân);
\(\angle ADH = \angle ACK\) (tính chất hình thang cân).
\( \Rightarrow \Delta ADH = \Delta BCK\) (cạnh huyền – góc nhọn) \( \Rightarrow DH = CK\) (hai cạnh tương ứng).
Mà \(DH + CK = CD - HK = 8 - 4 = 4\).
Do đó \(DH = CK = 2\).
Áp dụng định lí Pytago trong tam giác vuông \(ADH\) ta có:
\(A{H^2} = A{D^2} - D{H^2}\) \( \Leftrightarrow A{H^2} = {4^2} - {2^2} = 12\) \( \Leftrightarrow AH = 2\sqrt 3 \).
Vậy diện tích hình thang \(ABCD\) là: \({S_{ABCD}} = \dfrac{{\left( {AB + CD} \right).AH}}{2}\) \( = \dfrac{{\left( {4 + 8} \right).2\sqrt 3 }}{2} = 12\sqrt 3 \).
Câu hỏi 3 :
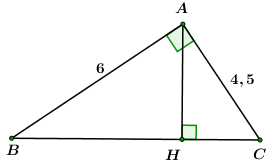
Cho tam giác \(ABC\) vuông tại \(A\), \(AB{\rm{ }} = {\rm{ 6}}cm,{\rm{ }}AC{\rm{ }} = 4,5cm.\)
Câu 1:
Tính các góc B, C và đường cao AH của tam giác.
- A \(\angle B = {53^0}8'\,\,;\,\,\,\angle C = {36^0}52'\,\,;\,\,AH = 3,6cm\)
- B \(\angle B = {36^0}52'\,\,;\,\,\,\angle C = {53^0}8'\,\,;\,\,AH = 3,6cm\)
- C \(\angle B = {48^0}35'\,\,;\,\,\,\angle C = {41^0}25'\,\,;\,\,AH = 3,6cm\)
- D \(\angle B = {41^0}25'\,\,;\,\,\,\angle C = {48^0}35'\,\,;\,\,AH = 3,6cm\)
Đáp án: B
Phương pháp giải:
Sử dụng định lý Pitago.
Sử dụng định nghĩa tỉ số lượng giác
Từ tỉ số lượng giác suy ra số đo góc
Sử dụng hệ thức lượng trong tam giác vuông : \(AH.BC = AB.AC\)
Công thức tính diện tích tam giác
Lời giải chi tiết:
Áp dụng định lý Pitago cho \(\Delta ABC\) vuông tại \(A\) có:
\(A{B^2} + A{C^2} = B{C^2}\) \( \Leftrightarrow B{C^2} = {6^2} + 4,{5^2} = 56,25\)\( \Rightarrow BC = 7,5\,\,cm.\)
Xét \(\Delta ABC\) vuông tại \(A\) ta có:
\(sinB = \frac{{AC}}{{BC}} = \frac{{4,5}}{{7,5}} = \frac{3}{5} \Rightarrow \angle B \approx {36^0}52'\)
Vì \(\Delta ABC\) vuông tại \(A\) ta có:
\(\angle B + \angle C = {90^0} \Leftrightarrow {36^0}52' + \angle C = {90^0}\)\( \Leftrightarrow \angle C \approx {53^0}8'\)
Áp dụng hệ thức lượng trong \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH\) ta có:
\(AH.BC = AB.AC\)\( \Leftrightarrow AH.7,5 = 4,5.6\)\( \Leftrightarrow AH = 3,6\)
Chọn B.
Câu 2:
Tính diện tích của tam giác ABC.
- A \(13,5c{m^2}\)
- B \(12,5c{m^2}\)
- C \(14,5c{m^2}\)
- D \(11,5c{m^2}\)
Đáp án: A
Phương pháp giải:
Sử dụng định lý Pitago.
Sử dụng định nghĩa tỉ số lượng giác
Từ tỉ số lượng giác suy ra số đo góc
Sử dụng hệ thức lượng trong tam giác vuông : \(AH.BC = AB.AC\)
Công thức tính diện tích tam giác
Lời giải chi tiết:
Ta có: \({S_{\Delta ABC}} = \frac{1}{2}.AH.BC = \frac{1}{2}.3,6.7,5 = 13,5\,\,c{m^2}.\)
Chọn A.
Câu hỏi 4 :
Dựng một cái thang lên tường với độ cao là 3m, thì khoảng cách từ chân thang tới chân tường tối thiểu là bao nhiêu để đảm bảo an toàn? Khi đó, em hãy tính chiều dài của cái thang? Biết rằng để có sự an toàn thì hệ số góc của cầu thang tối đa là 4.

- A 2,6m
- B 3,1m
- C 4m
- D 3,7m
Đáp án: B
Lời giải chi tiết:
Tìm khoảng cách từ chân thang tới chân tường tối thiểu để đảm bảo an toàn.
Gọi x là khoảng cách từ chân thang chân tường Xét hệ tọa độ Oxy như trong hình vẽ. Ta có: A(-x ; 0) là giao điểm của đường thẳng (diễn tả cái thang) với trục Ox và T(0; 3) là điểm thuộc đường thẳng có tung độ dương (giao điểm của cái thang với trục Oy). 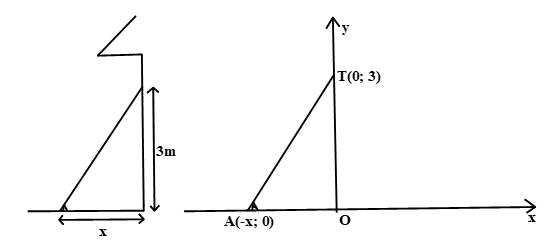
Vậy: Khoảng cách x tối thiểu từ chân thang tới chân tường phải là \(x = \dfrac{3}{4} = 0,75m\)
Tính chiều dài của cái thang
Ta có: OA = 0,75m, OT = 3m Áp dụng dịnh lý Pitago cho tam giác vuông AOT, vuông tại O, ta có:\(AT = \sqrt {O{A^2} + O{T^2}} = \sqrt {0,{{75}^2} + {3^2}} = 3,{1^{}}m\)
Vậy: Ứng với x = 0,75m thì chiều dài của cái thang khi đó là 3,1 m
Câu hỏi 5 :
Cho đường tròn (O, 5cm) và dây AB có độ dài là 8cm. Qua điểm B kẻ dây BC vuông góc với dây AB.
a) Tính độ dài dây BC.
b) Tính số đo góc BAC (làm tròn tới phút).
- A a) 6cm
b) \( 36^0 52'\)
- B a) 6cm
b) \( 72^0 52'\)
- C a) 2cm
b) \( 36^0 52'\)
- D a) 6cm
b) \( 45^0 52'\)
Đáp án: A
Lời giải chi tiết:
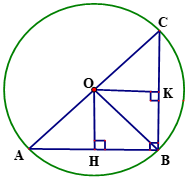
a) Tính độ dài dây BC
Kẻ \(OH \bot A{B^{}}^{}\left( {H \in AB} \right)\)\( \Rightarrow \) H là trung điểm AB (quan hệ đường kính, dây cung)
\( \Rightarrow HB = HA = \dfrac{{AB}}{2} = \dfrac{8}{2} = 4cm\)
Kẻ \(OK \bot B{C^{}}^{}\left( {K \in BC} \right)\)\( \Rightarrow \) K là trung điểm BC (quan hệ đường kính, dây cung)
Tứ giác OHBK là hình chữ nhật (vì có\(\widehat H = \widehat B = \widehat K = {90^0}\))\( \Rightarrow OK = HB = 4cm\)
Xét tam giác OBK, vuông tại K, áp dụng định lý Pitago ta có:\(KB = \sqrt {B{O^2} - O{K^2}} = \sqrt {{5^2} - {4^2}} = \sqrt 9 = 3cm\)
\(BC = 2KB = 2.3 = 6cm\) (K là trung điểm BC)
b) Tính số đo góc BAC (làm tròn tới phút)
Tam giác AOB cân tại O (vì OA = OB =R)\( \Rightarrow \) OH là đường cao nên OH cũng là phân giác \( \Rightarrow \) góc AOB = 2 góc HOB
Tam giác BOC cân tại O (vì OB = OC =R)\( \Rightarrow \) OK là đường cao nên OK cũng là phân giác \( \Rightarrow \) góc BOC = 2 góc KOB
Ta có: \(\angle AOB + \angle BOC = 2\angle HOB + 2\angle KOB = 2\left( {\angle HOB + \angle KOB} \right) = 2\angle HOK = {2.90^0} = {180^0}\)(Vì OHBK là hình chữ nhật \( \Rightarrow \angle HOK = {90^0}\))
\( \Rightarrow \) 3 điểm A, O, C thẳng hàng.
Xét tam giác vuông ACB, ta có:\(\tan BAC = \dfrac{{BC}}{{AB}} = \dfrac{6}{8} = \dfrac{3}{4} \Rightarrow \angle BAC = {36^0}52'\)
Câu hỏi 6 :
Cầu Mỹ Thuận là cây cầu dây văng bắc qua sông Tiền, nối liền hai tỉnh Tiền Giang và Vĩnh Long, Việt Nam. Cầu nằm cách Thành phố Hồ Chí Minh \(125km\) về hướng Tây Nam, trên Quốc lộ 1A, là trục giao thông chính của vùng đồng bằng sông Cửu Long. Cầu được hình khánh thành ngày \(21/5/2000\). Đây là cầu dây văng đầu tiên của Việt Nam.
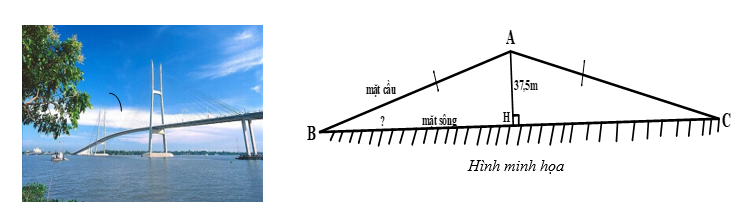
Nếu vẽ trên bản đồ tỉ lệ xích \(1:20000\) thì chiều dài của cây cầu trên bản đồ là \(7,676cm\) . Biết độ cao từ điểm cao nhất của mặt cầu và mặt sông là \(37,5m\). Em hãy tính góc tạo bởi mặt cầu và mặt sông? (hình minh họa)
- A \(15^0\)
- B \(2,8^0\)
- C \(0,8^0\)
- D \(10,8^0\)
Đáp án: B
Phương pháp giải:
Trong bài toán này, cái làm các em lúng túng không phải là phần kiến thức về Toán, mà là phần kiến thức về môn Địa Lý. Cụ thể, các em không nắm được tỉ lệ xích vẽ trên bản đồ với kích thước thực tế như thế nào.
Tỉ lệ xích của một bản vẽ (hoặc một bản đồ) là tỉ số khoảng cách \(a\) giữa hai điểm trên bản vẽ (hoặc trên bản đồ) và khoảng cách \(b\) giữa hai điểm tương ứng trên thực tế.
Lời giải chi tiết:
Bài giải chi tiết:
Do vẽ trên bản đồ tỉ lệ xích \(1:20000\) nên khi chiều dài của cây cầu trên bản đồ là \(7,676cm\) thì chiều dài thực tế của cây cầu Mỹ Thuận là:
\(7,676.20000 = 153520cm = 1535,2m\)
Từ hình minh họa đề cho, ta có cây cầu được chia thành hai đoạn \(AB\) và \(AC\) bằng nhau.
\( \Rightarrow AB = AC = \dfrac{{1535,2}}{2} = 767,6m\)
Xét tam giác vuông \(AHB\) , vuông tại \(H\) , ta có:
\(\sin ABH = \dfrac{{AH}}{{AB}} = \dfrac{{37,5}}{{767,6}} \approx 0,05 \Rightarrow \widehat {ABH} \approx 2,{8^0}\)
Vậy: Góc tạo bởi mặt cầu và mặt sông khoảng \(2,{8^0}\)
Câu hỏi 7 :
Cho tam giác \(ABC\) vuông tại \(A\) có \(AB = 9cm, BC = 15cm\) đường cao \(AH\).
a) Tính \(AH\) và \(CH\).
b) Qua \(B\) vẽ đường thẳng vuông góc với BC cắt đường thẳng \(AC\) tại \(D\). Tia phân giác của góc \(C\) cắt \(AB\) tại \(N\) và \(BD\) tại \(M\). Chứng minh \(CN.CD=CM.CB\).
c) Chứng minh \(\dfrac{{NA}}{{MD}} = \dfrac{{CA}}{{CD}}\).
- A a) \(AH = 9,6cm; CH = 7,2cm\)
- B a) \(AH = 7,2cm; CH = 9,6\)
- C a) \(AH = 4,8cm; CH = 9,6cm\)
- D a) \(AH = 4,8cm; CH = 7,2cm\)
Đáp án: B
Lời giải chi tiết:
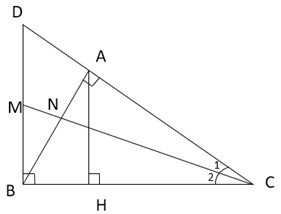
a) Theo định lý Py – ta – go ta có: \(A{C^2} = B{C^2} - A{B^2} = {15^2} - {9^2} = 144 \Rightarrow AC = 12\,\,\left( {cm} \right)\).
Tam giác ABC vuông tại A có đường cao AH, ta có: \(AH.BC=AB.AC\).
\(\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{9.12}{15}=7,2\,\,\left( cm \right)\).
Áp dụng hệ thức lượng trong tam giác vuông, ta có: \(A{{C}^{2}}=BC.CH\Rightarrow CH=\dfrac{A{{C}^{2}}}{BC}=\dfrac{{{12}^{2}}}{15}=9,6\,\,\left( cm \right)\).
b) Ta có: \(\angle {{C}_{1}}=\angle {{C}_{2}}\,\,\left( gt \right)\Rightarrow \Delta CAN\sim \Delta CBM\,\,\left( g.g \right)\Rightarrow \dfrac{CN}{CM}=\dfrac{CA}{CB}\,\,\left( 1 \right)\).
Dễ thấy \(\Delta CAB\sim \Delta CBD\,\,\left( g.g \right)\Rightarrow \dfrac{CA}{CB}=\dfrac{CB}{CD}\,\,\left( 2 \right)\).
Từ (1) và (2) \(\Rightarrow \dfrac{CN}{CM}=\dfrac{CB}{CD}\Rightarrow CN.CD=CM.CB\).
c) Vì ∆CAN đồng dạng với ∆CBM (cmt) ta có: \(\dfrac{NA}{CA}=\dfrac{MB}{CB}\,\,\left( 3 \right)\).
Tia CM là phân giác của góc BCD (gt) nên \(\dfrac{{MB}}{{MD}} = \dfrac{{CB}}{{CD}} \Leftrightarrow \dfrac{{MB}}{{CB}} = \dfrac{{MD}}{{CD}}\,\,\left( 4 \right)\).
Từ (3) và (4) \( \Rightarrow \dfrac{{NA}}{{CA}} = \dfrac{{MD}}{{CD}} \Rightarrow \dfrac{{NA}}{{MD}} = \dfrac{{CA}}{{CD}}\).
Câu hỏi 8 :
Cho tam giác MNP có MN = 3cm; MP = 4cm; NP = 5cm.
a) Chứng minh rằng tam giác MNP là tam giác vuông
b) Kẻ đường cao MK. Gọi D và E lần lượt là hình chiếu của K trên MN và MP. Tính DE
c) Chứng minh rằng:MD.MN = ME. MP
d) Chứng minh rằng: ND.PE.NP = MK3
Lời giải chi tiết:

Câu hỏi 9 :
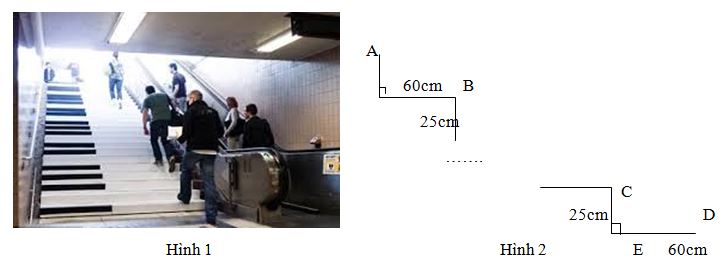
Cầu thang bộ của bigC nguyễn Kiệm (ảnh minh họa như hình 1 bên trái) gồm 20 bậc có kích thước và mô tả như hình 2 ( bề rộng bậc thang là 60cm,chiều cao giữa hai bậc là 25cm). Nếu siêu thị cho lắp thang máy (ảnh minh họa như hình 1 bên phải) thì chiều dài của cầu thang máy là bao nhiêu, giả sử rằng thang máy phẳng đều và đi qua khít các điểm A,B,C,D,…xem phần hở không đáng kể. Điểm cao nhất của thang máy là A, điểm thấp nhất của thang máy là D.
- A 13m
- B 15m
- C 11m
- D 9m
Đáp án: A
Phương pháp giải:
Phân tích:
Đây là bài toán tương tự như bài về đường đi của con rô bốt trong đề minh họa của sở GD Tuy nhiên, nếu giải theo phương pháp dựng thêm hình thì sẽ làm bài toán trở nên khó hơn với một số học sinh vì phải chứng minh phần vuông góc tại H ( mặc dù nhìn là biết vuông góc rồi!) Để giải nhanh bài này, ta tinh ý sẽ phát hiện ra 20 tam giác vuông bằng nhau. Từ đó, độ dài băng tải sẽ gấp 20 lần độ dài của một cạnh huyền của một tam giác vuông.
Lời giải chi tiết:
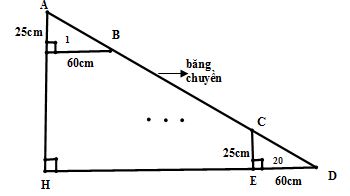
Cách 1:
Xét các tam giác vuông có số thứ tự từ 1 đến 20, ta có chúng bằng nhau theo trường hợp:
cạnh- góc – cạnh (có các góc vuông bằng nhau, có cách cạnh góc vuông độ dài 25cm và các cạnh góc vuông độ dài 60cm bằng nhau)
Xét vuông CDE, áp dụng định lý pitago ta có:
\( \eqalign{& \,\,\,\,\,\,\,\,C{D^2} = C{E^2} + D{E^2} \cr & \Rightarrow C{D^2} = {25^2} + {60^2} \cr & \Rightarrow C{D^2} = 4225 \cr & \Rightarrow CD = 65cm \cr} \)
Vì 20 tam giác bằng nhau, nên chiều dài của thang máy gấp 20 lần độ dài cạnh huyền của một tam giác vuông, vậy chiều dài của thang máy là: AD = 20.65 = 1300cm = 13m
Cách 2:
Gọi H là hình chiếu vuông góc của A lên đường thẳng DE
tại H vuông tại H
Độ dài đoạn AH là: AH = 25.20 = 500cm = 5m
Độ dài đoạn DH là: DH = 60.20 = 1200cm = 12m
Xét vuông AHD, áp dụng định lý pitago ta có:
\( \eqalign{ & \,\,\,\,\,\,\,\,A{D^2} = A{H^2} + H{D^2} \cr & \Rightarrow A{D^2} = {5^2} + {12^2} \cr & \Rightarrow A{D^2} = 169 \cr & \Rightarrow AD = 13m \cr} \)
Vậy: Chiều dài của thang máy là: AD = 13m.
Câu hỏi 10 :
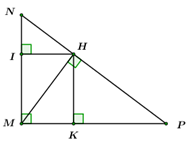
Tại một vị trí trên bờ, bạn An có thể xác định được khoảng cách hai chiếc thuyền ở vị trí A, vị trí B bằng cách như sau: Trước tiên, bạn chọn một vị trí trên bờ ( điểm I) sao cho ba điểm I, A, B thẳng hàng. Sau đó, bạn di chuyển theo hướng vuông góc với IA đến vị trí điểm K cách điểm I khoảng \(380m\). Bạn dùng giác kế nhắm vị trí điểm A, điểm B thì đo được góc \({{15}^{0}}\). Còn khi bạn nhắm vị trí điểm A, điểm I thì đo được góc \({{50}^{0}}\). Hỏi khoảng cách hai chiếc thuyền là bao nhiêu?
- A \(362m\)
- B \(256m\)
- C \(200m\)
- D \(300m\)
Đáp án: A
Phương pháp giải:
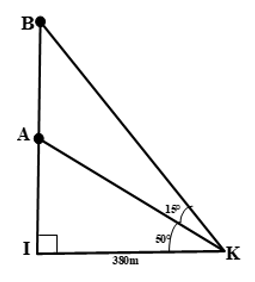
Phân tích bài toán:
Đây là một bài tập theo đúng nghĩa là ứng dụng thực tế. Một bài tập về dùng giác kế để đo góc, rồi dùng các tỉ số lượng giác trong tam giác vuông để tính ra khoảng cách giữa các vật. Phương pháp đo này dùng để đo những đối tượng thường là bị ngăn cách mà ta không thể sử dụng thước để đo trực tiếp được, ví dụ: đo khoảng cách giữa hai ngọn núi, khoảng cách giữa hai chiếc thuyền trên biển hay đo chiều cao của một cái cây chẳng hạn. Khi giải bài tập loại này các em chỉ cần sử dụng tỉ số lượng giác trong tam giác vuông là làm được.
Lời giải chi tiết:
Do KA nằm giữa KI và KB nên:
\(\widehat{BKI}=\widehat{BKA}+\widehat{AKI}={{15}^{0}}+{{50}^{0}}={{65}^{0}}\). Xét tam giác vuông AKI, vuông tại I, ta có: \(\tan AKI=\dfrac{AI}{IK}\Rightarrow AI=IK.\tan AKI=380.\tan {{50}^{0}}\) (mét) Xét tam giác vuông BKI, vuông tại I, ta có: \(\tan BKI=\dfrac{BI}{IK}\Rightarrow BI=IK.\tan BKI=380.\tan {{65}^{0}}\) (mét) Khoảng cách hai chiếc thuyền chính là độ dài đoạn AB:
\(AB=BI-AI=380.\tan{{65}^{0}}-380.\text{ }\tan{{50}^{0}}=380.\left( \tan{{65}^{0}}-\tan{{50}^{0}} \right)=362\) (mét)
Câu hỏi 11 :
Tòa nhà Bitexco Financial (hay Tháp Tài chính Bitexco) là một tòa nhà chọc trời được xây dựng tại trung tâm Quận 1, Thành phố Hồ Chí Minh. Tòa nhà có 68 tầng (không tính 3 tầng hầm). Biết rằng, khi toà nhà có bóng in trên mặt đất dài 47,5 mét, thì cùng thời điểm đó có một cột cờ (được cắm thẳng đứng trên mặt đất) cao 12 mét có bóng in trên mặt đất dài 2,12 mét. a) Tính góc tạo bởi tia nắng mặt trời với mặt đất (đơn vị đo góc được làm tròn đến độ). b) Tính chiều cao của toà nhà, (làm tròn đến chữ số thập phân thứ nhất).

- A a) Vậy: Góc tạo bởi tia nắng mặt trời và mặt đất là 800
b) Tòa nhà Bitexco cao 269m
- B a) Vậy: Góc tạo bởi tia nắng mặt trời và mặt đất là 850
b) Tòa nhà Bitexco cao 296m
- C a) Vậy: Góc tạo bởi tia nắng mặt trời và mặt đất là 900
b) Tòa nhà Bitexco cao 296m
- D a) Vậy: Góc tạo bởi tia nắng mặt trời và mặt đất là 600
b) Tòa nhà Bitexco cao 269m
Đáp án: A
Phương pháp giải:
Phân tích bài toán:
Để làm được bài tập này, trước hết các em phải nắm được tính chất của tia nắng mặt trời là các tia song song (sách vật lý 7- hk1). Do đó, ở cùng một thời điểm thì góc tạo bởi tia nắng mặt trời và mặt đất là như nhau tại mọi vị trí. Điểm khó khăn thứ hai là từ đề bài các em phải vẽ ra được hình minh họa cho bài toán. Khi đã có hình vẽ cho bài toán thì các em chỉ cần sử dụng tỉ số lượng giác trong tam giác vuông là ra được đáp án.
Lời giải chi tiết:
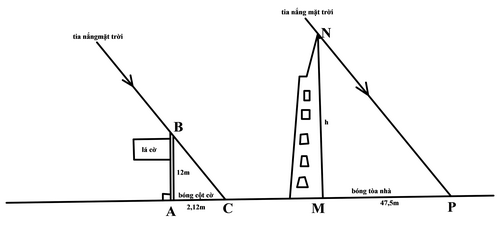
Hình minh họa
a) Tính góc tạo bởi tia nắng mặt trời với mặt đất (đơn vị đo góc được làm tròn đến độ).
Gọi h là chiều cao của tòa nhà Bitexco Vì mặt trời ở rất xa trái đất nên chùm sáng mà mặt trời phát ra xem như là chùm sáng song song Do đó, ở cùng một thời điểm thì góc tạo bởi tia sáng mặt trời và mặt đất là như nhau Xét tam giác vuông ABC, ta có:\(\tan ACB = \frac{{AB}}{{AC}} = \frac{{12}}{{2,12}} = 5,66 \Rightarrow ACB = {80^0}\)
Vậy: Góc tạo bởi tia nắng mặt trời và mặt đất là 800
b) Tính chiều cao của toà nhà Bitexco, (làm tròn đến chữ số thập phân thứ nhất).
Do góc tạo bởi tia sáng mặt trời và mặt đất là như nhau
\( \Rightarrow \mathop {ACB}\limits^\^ = \mathop{MPN}\limits^\^ \Rightarrow \tan ACB = \tan MPN = 5,66\)
Xét tam giác vuông MPN, ta có: \({\mathop{\rm tanMPN}\nolimits} = \frac{{MN}}{{MP}} \Leftrightarrow 5,66 = \frac{h}{{47,5}} \Leftrightarrow h = 5,66.47,5 = 269m\)
Vậy: Tòa nhà Bitexco cao 269m.
Câu hỏi 12 :
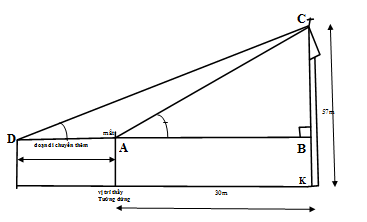
Nhà thờ Đức Bà tọa lạc tại Số 1, Công Xã Paris, Phường Bến Nghé, Quận 1, Hồ Chí Minh. Với chiều cao 57m ( từ chân nhà thờ đến cây thánh giá trên đỉnh), quang cảnh rộng lớn, giao lộ thông thoáng, được bao quanh bởi hàng cây tươi xanh, ít có tòa nhà cao tầng. Nhà thờ Đức Bà nổi bậc như một công trình kiến trúc đồ sộ, trang nghiêm bậc nhất trong khu vực này.
Trong một dịp tới tham quan nhà thờ, khi đứng trên mặt đất cách nhà thờ 30m, thầy Tưởng có thể nhìn thấy được cây thánh giá trên đỉnh của nhà thờ.
a) Thầy Tưởng nhìn đỉnh của nhà thờ với “góc nâng” ( làm tròn số đo góc đến phút) là:
b) Nếu thầy Tưởng dịch chuyển một đoạn để góc nâng là 500 mà vẫn có thể nhìn thấy được cây thánh giá trên đỉnh của nhà thờ( biết thầy Tưởng cao 1,7m và khoảng cách từ mắt đến đỉnh đầu là 10cm) thì thầy phải di chuyển lại gần hay ra xa nhà thờ một đoạn là:
- A a) \({{60}^{0}}33'\)
b) \(16.5 m\)
- B a) \({{61}^{0}}33'\)
b) \(16.5 m\)
- C a) \({{61}^{0}}\)
b) \(16.5 m\)
- D a) \({{61}^{0}}33'\)
b) \(16 m\)
Đáp án: B
Phương pháp giải:
• Đây là một bài tập thực tế vận dụng kiến tỉ số lượng giác trong tam giác vuông.
• Về mặt tính toán, bài toán áp dụng một vài công thức đơn giản sẽ ra được đáp số.
Lời giải chi tiết:
a) Hỏi thầy Tưởng nhìn đỉnh của nhà thờ với “góc nâng” là bao nhiêu? ( làm tròn số đo góc đến phút)
• Khoảng các từ mắt đến chân thầy Tưởng: 1,7 – 0,1 = 1,6m
• Độ dài đoạn BC: 57 – 1,6 = 55,4m
• Xét tam giác vuông ABC vuông tại B, ta có:
\(\tan BAC=\frac{BC}{AB}=\frac{55,4}{30}\) \(\Rightarrow \) góc \(BAC={{61}^{0}}33'\)Vậy: Góc “nâng” từ chỗ thầy Tưởng đứng đến đỉnh của nhà thờ là: \({{61}^{0}}33'\)
b) Nếu thầy Tưởng dịch chuyển một đoạn để “góc nâng” là 500 mà vẫn có thể nhìn thấy được cây thánh giá trên đỉnh của nhà thờ, thì thầy phải di chuyển lại gần hay ra xa nhà thờ một đoạn là bao nhiêu mét?
• Gọi D là vị trí mà thầy Tưởng di chuyển tới sau đó để góc “nâng” là 500
• Xét tam giác vuông BCD vuông tại B, ta có:
\(\tan BDC=\frac{BC}{BD}\Rightarrow BD=\frac{BC}{\operatorname{t}\text{an5}{{\text{0}}^{0}}}=\frac{55,4}{\operatorname{t}\text{an5}{{\text{0}}^{0}}}=46,5m>30m\)
Vậy: Thầy Tưởng phải di chuyển ra xa nhà thờ một đoạn: 46,5 – 30 = 16,5m
Chọn B
Câu hỏi 13 :
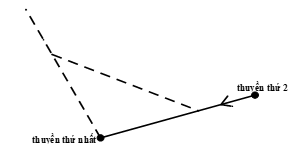
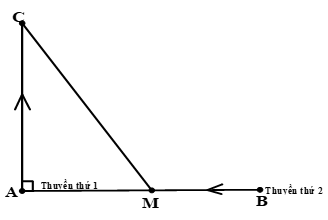
Hai chiếc thuyền đang ở cùng một vĩ tuyến, cách nhau một khoảng \(9\) hải lý. Vào lúc \(6h\) cả hai cùng xuất phát, chiếc thuyền thứ nhất đi theo hướng Bắc với vận tốc \(6\) hải lý/ giờ. Chiếc thuyền thứ hai đi theo hướng về vị trí ban đầu của chiếc thuyền thứ nhất với vận tốc \(4\) hải lý/ giờ. Hỏi đến \(6h45\) phút thì khoảng cách giữa hai chiếc thuyền là bao nhiêu km? Biết \(1\) hải lý \( = 1852m\)
- A \(7,5km\)
- B \(13,89km\)
- C \(14,89km\)
- D \(13km\)
Đáp án: B
Phương pháp giải:
Điểm mấu chốt của bài toán nằm ở việc hiểu được “hai thuyền ở cùng một vĩ tuyến” là như thế nào?
Các em lưu ý, trong môn Địa Lý vĩ tuyến là các đường nằm theo chiều ngang của Trái Đất.
(cụ thể có 5 đường vĩ tuyến, trong đó, có một đường vĩ tuyến mà em nào cũng biết đó là đường xích đạo- các em tìm hiểu kỹ trong môn Địa Lý nhé!)
Sau khi đã biết về đường vĩ tuyến và phương hướng trên Trái Đất các em phải vẽ lại hình cho bài toán để dựa vào đó giải ra đáp số.
Lời giải chi tiết:
Vẽ lại sơ đồ bài toán như hình vẽ:
Vì lúc đầu hai chiếc thuyền ở cùng một vĩ tuyến ta biễu diễn theo phương ngang \(AB\)
Sau khi xuất phát, thuyền thứ hai đi về hướng Bắc nên ta biểu diễn theo hướng \(AC\) hướng thẳng lên
Thuyền thứ hai đi trở về vị trí thuyền thứ nhất tức là hướng từ \(B\) sang \(A\)
Hướng Nam-Bắc vuông góc với vĩ tuyến nên \(AB\) vuông góc với \(AC\) tại \(A\) .
\(AB = 9\) hải lý là khoảng cách lúc đầu giữa hai thuyền.
\(AC\) là quãng đường thuyền thứ nhất đi được, \(BM\) là quãng đường thuyền thứ hai đi được trong cùng một khoảng thời gian.
\(CM\) là khoảng cách giữa hai thuyền lúc sau.
Thời gian đi của hai thuyền
t = 6h45phút – 6h = 45phút = \(\dfrac{3}{4}h\)
Quãng đường mà thuyền thứ nhất đi được:
\(AC = {v_1}.{\text{ }}t = 6.\dfrac{3}{4} = 4,5\) ( hải lý)
Quãng đường mà thuyền thứ hai đi được:
\(BM = {v_1}.{\text{ }}t = 4.\dfrac{3}{4} = 3\) ( hải lý)
Độ dài đoạn \(AM\) :
\(AM = \;9-3 = 6\) (hải lý)
Xét \(\Delta ABM\)vuông tại \(A\) , áp dụng định lý Pitago, ta có:
\(A{M^2} + A{C^2} = C{M^2} \Leftrightarrow C{M^2} = 4,{5^2} + {6^2} = 56,25 \Leftrightarrow CM = 7,5\) (hải lý)
\(7,5\) (hải lý) \( = 7,5.1,852\) km \( = 13,89\) km (\(1\) hải lý\( = 1852m = 1,852km\))
Vậy: Đến \(6h45\) phút thì khoảng cách giữa hai chiếc thuyền là \(13,89\)km.
Câu hỏi 14 :
Chơi xích đu là một trò chơi quen thuộc với nhiều người. Cô Loan cũng vậy, tuy đã lớn, nhưng ngồi xích đu luôn làm cô thấy thú vị sau mỗi ngày làm việc căng thẳng trên tuyển sinh 247.
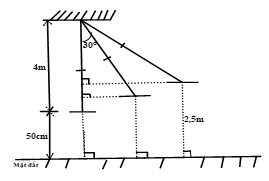
Biết ở vị trí cân bằng dậy xích đu vuông góc với mặt đất, ghế xích đu cách mặt đất 50cm. Dây xích đu từ điểm treo đến ghế dài 4m và không giãn.
a) Khi dây xích đu hợp với phương thẳng đứng 300 thì ghế xích đu cách mặt đất một khoảng bao nhiêu mét?
b) Khi ghế xích đu cách mặt đất một khoảng 2,5m thì dây xích đu hợp với phương thẳng đứng góc bao nhiêu độ? Xem như độ dày của ghế xích đu không đáng kể.
- A a) 3m
b) \(40^0\)
- B a) 1m
b) \(30^0\)
- C a) 2m
b) \(30^0\)
- D a) 1m
b) \(60^0\)
Đáp án: D
Lời giải chi tiết:
a) Khi dây xích đu hợp với phương thẳng đứng góc 300 thì ghế xích đu cách mặt đất một khoảng bao nhiêu mét?
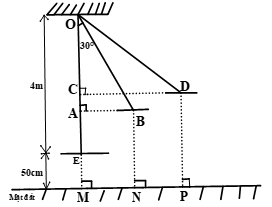
Đặt các điểm tương ứng trên hình vẽ minh họa. Do dây không giãn nên: OE = OB = OD = 4m Xét tam giác vuông OAB, ta có:
\(\cos \widehat O = \dfrac{{OA}}{{OB}} \Rightarrow OA = OB.\cos \widehat O = 4.\cos {30^0} \approx 3,5m\)
\(AE = OE - OA = 4 - 3,5 = 0,5m\)
Ghế xích đu cách mặt đất một khoảng:
\(AM = BN = AE + EM = 0,5 + 0,5 = 1m\)
(Do tứ giác AMNB là hình chữ nhật (có \(\widehat A = \widehat M = \widehat N = {90^0}\)) nên AM =BN)
Vậy: Khi dây xích đu hợp với phương thẳng đứng 300 thì ghế xích đu cách mặt đất một khoảng 1m
b) Khi ghế xích đu cách mặt đất một khoảng 2,5 m thì dây xích đu hợp với phương thẳng đứng góc bao nhiêu độ?
Ta có: DP = 2,5m (gt) Tứ giác CMPD là hình chữ nhật (vì có\(\widehat C = \widehat M = \widehat P = {90^0}\)) nên: DP = CM = 2,5m
\(OC = OM - CM = \left( {4 + 0,5} \right) - 2,5 = 2m\)
Xét tam giác vuông OCD, ta có: \(\cos COD = \dfrac{{OC}}{{OD}} = \dfrac{2}{4} = 0,5 \Rightarrow \angle COD = {60^0}\)
Vậy: Khi ghế xích đu cách mặt đất một khoảng 2,5 m thì dây xích đu hợp với phương thẳng đứng góc 600
Câu hỏi 15 :
Trong buổi tập luyện, một tàu ngầm đang ở trên mặt biển bắt đầu lặn xuống và di chuyển theo đường thẳng tạo với mặt nước biển một góc 210 (xem hình bên).
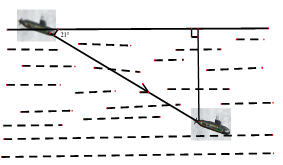
a) Khi tàu chuyển động theo hướng đó và đi được 200m thì tàu sẽ ở độ sâu bao nhiêu so với mặt nước biển (làm tròn đến đơn vị mét)
b) Giả sử tốc độ trung bình của tàu là 9 km/h, thì sau bao lâu (tính từ lúc bắt đầu lặn) tàu ở độ sâu 200m (cách mặt nước biển 200m)? (làm tròn đến phút).
Lời giải chi tiết:
a)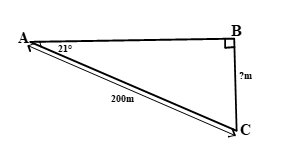
Đặt vị trí các điểm trên hình vẽ minh họa như hình bên. A là vị trí tàu bắt đầu lặn, tàu lặn theo phương trùng đoạn thẳng AC với AC = 200m, góc BAC =210. Xét tam giác ABC vuông tại B, ta có:
\(\sin BAC=\frac{BC}{AC}\Rightarrow BC=AC.\sin BAC=200.\sin {{21}^{0}}\approx 72m\)
Vậy: Khi tàu chuyển động theo phương AC và đi được 200m thì tàu đang ở độ sâu khoảng 72m so với mặt nước biển.
b)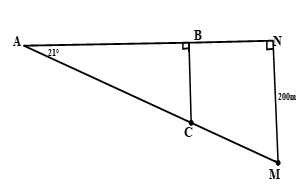
Tàu tiếp tục chuyển động theo phương AC và tới điểm M có độ sâu so với mặt nước biển bằng đoạn MN =200m như hình vẽ. Xét tam giác AMN vuông tại N, ta có:
\(\sin NAM=\frac{MN}{AM}\Leftrightarrow AM=\frac{MN}{\sin NAM}=\frac{200}{\sin {{21}^{0}}}=558m=0,558km\)
Thời gian để tàu di chuyển được quãng đường AM là:
\(t=\frac{AM}{v}=\frac{0,558}{9}=0,062\left( h \right)\approx 4\) (phút)
Vậy: Sau gần 4 phút (tính từ lúc bắt đầu lặn) thì tàu ở độ sâu 200m (so với mặt nước biển).
Câu hỏi 16 :
Đám đất nhà bạn Tý có dạng hình tứ giác ABCD trong đó AC dài 32m, BD dài 24m và AC vuông góc với BD. Mẹ bạn Tý cho trồng hai cây cau tại điểm M và N lần lượt là trung điểm của các cạnh AB, CD. Hỏi khoảng cách giữa hai cây cau là bao nhiêu mét?
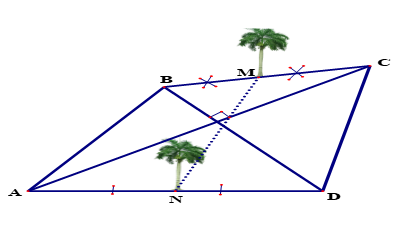
- A 10 mét
- B 20 mét
- C 15 mét
- D 25 mét
Đáp án: B
Lời giải chi tiết:
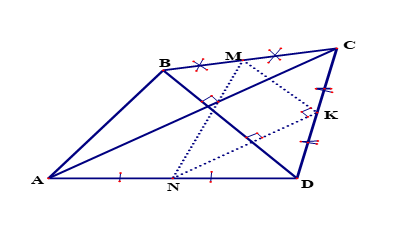
N là trung điểm AD và K là trung điểm CD .
\(\Rightarrow NK\) là đường trung bình của \(\Delta ACD\)
\(\Rightarrow NK=\frac{1}{2}AC=\frac{1}{2}.32=16m\)
và NK // AC mà \(AC\bot BD\Rightarrow NK\bot BD\)(quan hệ vuông góc song song)
Xét tam giác BCD, ta có:
M là trung điểm BC và K là trung điểm CD.
\(\Rightarrow MK\) là đường trung bình của \(\Delta BCD\)
\(\Rightarrow MK=\frac{1}{2}BD=\frac{1}{2}.24=12m\)
và MK // BD mà \(NK\bot BD\Rightarrow NK\bot MK\) (quan hệ vuông góc song song)
\(\Rightarrow \Delta MNK\) vuông tại K.
Áp dụng dịnh lý Pitago cho tam giác vuông MNK, ta có:\(MN=\sqrt{N{{K}^{2}}+M{{K}^{2}}}=\sqrt{{{16}^{2}}+{{12}^{2}}}=20m\)
Vậy hai cây cau cách nhau một đoạn MN bằng 20 mét.
Câu hỏi 17 :
Thầy Tưởng có ý định xây dựng một căn nhà như hình bên, biết AD =15m, BC = 8m. Hai mái nhà là các hình chữ nhật, góc ABC = 400, góc ACB = 450.
Em hãy tính tổng diện tích phần mái nhà mà thầy Tưởng muốn xây dựng.
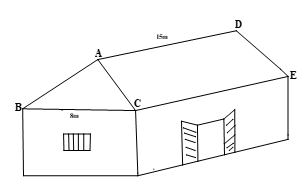
Lời giải chi tiết:

Gọi AH là đường cao của \(\Delta ABC\)
Xét tam giác vuông AHB, vuông tại H , ta có:
\(\cot ABH=\frac{BH}{AH}\Leftrightarrow BH=AH.\cot ABH\)
Xét tam giác vuông AHC, vuông tại H , ta có:\(\cot ACH=\frac{HC}{AH}\Leftrightarrow HC=AH.\cot ACH\)
Ta có: BC = BH + HC
\(\begin{array}{l}\Leftrightarrow BC = AH.\cot ABH + AH.\cot ACH\\ \Leftrightarrow BC = AH.\left( {\cot ABH + \cot ACH} \right)\\ \Leftrightarrow AH = \frac{{BC}}{{\cot ABH + \cot ACH}} = \frac{8}{{\cot {{40}^0} + \cot {{45}^0}}} \approx 3,65m\end{array}\)
Xét tam giác vuông AHB, vuông tại H , ta có:\(\sin ABH=\frac{AH}{AB}\Leftrightarrow AB=\frac{AH}{\sin ABH}=\frac{3,65}{\operatorname{s}\text{in4}{{0}^{0}}}\approx 5,68m\)
Xét tam giác vuông AHC, vuông tại H , ta có:\(\sin ACH=\frac{AH}{AC}\Leftrightarrow AC=\frac{AH}{\sin ACH}=\frac{3,65}{\operatorname{s}\text{in4}{{\text{5}}^{0}}}\approx 5,16m\)
Tổng diện tích phần mái nhà mà thầy Tưởng muốn xây dựng là:\(S=AB.AD+AC.AD=5,68.15+5,16.15=162,6{{m}^{2}}\)
Câu hỏi 18 :
Từ nóc một cao ốc cao 30m người ta nhìn thấy chân và đỉnh
của một cột ăng-ten (cắm vuông góc với mặt đất) với các góc hạ
và nâng lần lượt là 40 và 50 .
Tính chiều cao của cột ăng-ten (kết quả làm tròn đến hàng đơn vị).
(Hình bên) 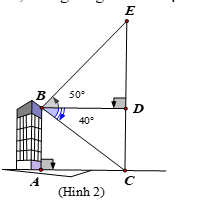
Lời giải chi tiết:
Ta có: số đo góc CBE = 400 + 500 = 900
\(\Rightarrow \Delta EBC\) vuông tại B.
Tứ giác ABDC là hình chữ nhật (vì có \(\overset{\hat{\ }}{\mathop{A}}\,=\overset{\hat{\ }}{\mathop{C}}\,=\overset{\hat{\ }}{\mathop{D}}\,={{90}^{0}}\))
\(\Rightarrow AB=CD=30m\)
Xét tam giác BCD vuông tại D, ta có:
\(\sin CBD=\frac{CD}{BC}\Rightarrow BC=\frac{CD}{\sin CBD}=\frac{30}{\sin {{40}^{0}}}\)
Xét tam giác vuông EBC, ta có:
\(B{{C}^{2}}=CD.CE\) (Hệ thức lượng trong tam giác vuông)
\(\Rightarrow CE=\frac{B{{C}^{2}}}{CD}=\frac{{{\left( \frac{30}{\sin {{40}^{0}}} \right)}^{2}}}{30}\approx 73m\)
v Vậy chiều cao của cột ăng-ten gần bằng 73 mét.
Câu hỏi 19 :
Hải Đăng Đa Lát là một trong bảy ngọn núi cao nhất việt Nam, được đặt trên đảo Đa Lát ở vị trí cực Tây quần đảo, thuộc xã đảo Trường Sa, huyện Trường Sa, tỉnh Khánh Hòa. Ngọn Hải Đăng được xây dựng năm 1994, cao 42m, có tác dụng chỉ vị trí đảo, giúp tàu bè hoạt động trong vùng biển Trường Sa định hướng và xác định được vị trí của mình. Một người đi tàu trên biển muốn đến Hải Đăng Đa Lát, người đó đứng trên mũi tàu và dùng giác kế đo được góc giữa mũi tàu và tia nắng chiếu từ đỉnh ngọn hải đăng đến tàu là 100.
a) Tính khoảng cách từ tàu đến ngọn hải đăng? (kết quả làm tròn đến một chữ số thập phân)
b) Trên tàu còn 1 lít dầu, cứ đi 10m thì tàu đó hao tốn hết 0,02 lít dầu. Hỏi tàu đó có đủ dầu để đến ngọn hải đăng Đa Lát hay không?

- A 236,2m
Tàu đủ dầu chạy đến ngọn đăng
- B 238,2m
Tàu không đủ dầu chạy đến ngọn đăng
- C 458,2m
Tàu không đủ dầu chạy đến ngọn đăng
- D 238,2m
Tàu đủ dầu chạy đến ngọn đăng
Đáp án: D
Lời giải chi tiết:
a)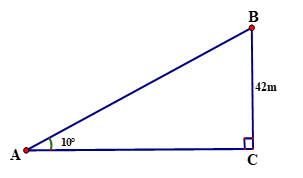
Biểu diễn bài toán bằng hình vẽ như hình bên.
v Trong đó:
A là vị trí mũi tàu, BC = 42m là chiều cao của ngọn hải đăng Đa Lát, góc BAC = 100là góc giữa mũi tàu và tia nắng chiếu từ đỉnh ngọn hải đăng đến tàu theo phương AB. Khoảng cách từ tàu đến ngọn hải đăng là độ dài đoạn AC Xét tam giác ABC vuông tại C, ta có:
\(\tan BAC=\frac{BC}{AC}\Leftrightarrow AC=\frac{BC}{\tan BAC}=\frac{42}{\tan {{10}^{0}}}\approx 238,2m\)
Vậy: Khoảng cách từ tàu đến ngọn hải đăng xấp xỉ bằng 238,2m
b)
Cứ hao tốn 0,02 lít dầu thì tàu chạy được 10m
\(\Rightarrow \) 1 lít dầu tàu chạy được quãng đường dài là: \(\frac{1.10}{0,02}=500m\)
Do 500m > 238,2m nên tàu có đủ dầu để chạy đến ngọn hải đăng Đa Lát.
Câu hỏi 20 :
Cho \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH\)và đường trung tuyến \(AM\). Biết \(AH = 3cm;\,HB = 4cm.\) Hãy tính \(AB,AC,AM\) và diện tích tam giác \(ABC.\)
- A \(AB = 5cm,\,\,AC = \frac{{15}}{4}cm,\,\,AM = \frac{{25}}{8}cm,\,\,{S_{\Delta ABC}} = \frac{{75}}{8}\,\,c{m^2}\)
- B \(AB = 5cm,\,\,AC = 3cm,\,\,AM = 4cm,\,\,{S_{\Delta ABC}} = \frac{{39}}{4}\,\,c{m^2}\)
- C \(AB = \frac{{14}}{3}cm,\,\,AC = \frac{{14}}{4}cm,\,\,AM = 3cm,\,\,{S_{\Delta ABC}} = \frac{{75}}{8}\,\,c{m^2}\)
- D \(AB = \frac{{14}}{3}cm,\,\,AC = 3cm,\,\,AM = \frac{{27}}{8}cm,\,\,{S_{\Delta ABC}} = 9\,\,c{m^2}\)
Đáp án: A
Lời giải chi tiết:
+) Áp dụng định lý Pytago trong tam giác vuông ABH vuông tại H ta có:
\(\,\,\,\,\,\,\,A{B^2} = A{H^2} + H{B^2} = {3^2} + {4^2} = 25 \Rightarrow AB = 5\,\,\,\left( {cm} \right)\).
+) Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông ABC với AH là đường cao ta có:
\(\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} \Leftrightarrow \frac{1}{{A{C^2}}} = \frac{1}{{A{H^2}}} - \frac{1}{{A{B^2}}} \Leftrightarrow \frac{1}{{A{C^2}}} = \frac{1}{{{3^2}}} - \frac{1}{{{5^2}}} = \frac{{16}}{{225}} \Rightarrow AC = \frac{{15}}{4}\left( {cm} \right)\)
+) Áp dụng định lý Pytago trong tam giác vuông ABC vuông tại A ta có:
\(B{C^2} = A{B^2} + A{C^2} = {5^2} + {\left( {\frac{{15}}{4}} \right)^2} = \frac{{625}}{{16}} \Rightarrow BC = \frac{{25}}{4}\left( {cm} \right)\).
+) Tam giác ABC vuông tại A có trung tuyến AM nên ta có: \(AM = \frac{1}{2}BC = \frac{{25}}{8}\,\,\,\left( {cm} \right)\)
+) Diện tích tam giác ABC với AH là đường cao ta có: \({S_{ABC}} = \frac{1}{2}AH.BC = \frac{1}{2}.3.\frac{{25}}{4} = \frac{{75}}{8}\,\,\left( {c{m^2}} \right)\).
Vậy \(AB = 5cm,\,\,AC = \frac{{15}}{4}cm,\,\,AM = \frac{{25}}{8}cm,\,\,{S_{\Delta ABC}} = \frac{{75}}{8}\,\,c{m^2}\)
Chọn A.
Câu hỏi 21 :
Cho tam giác \(ABC\) có \(AB = 4cm,\,\,\,AC = 4\sqrt 3 ,\,\,BC = 8cm.\)
a) Chứng minh tam giác \(ABC\) vuông.
b) Tính số đo \(\angle B,\,\,\angle C\) và độ dài đường cao \(AH\) của \(\Delta ABC.\)
- A \({\rm{b)}}\,\,\angle B = {45^0}\,\,;\,\,\angle C = {45^0}\,\,;\,\,AH = \sqrt 3 \)
- B \({\rm{b)}}\,\,\angle B = {50^0}\,\,;\,\,\angle C = {40^0}\,\,;\,\,AH = 2\)
- C \({\rm{b)}}\,\,\angle B = {30^0}\,\,;\,\,\angle C = {60^0}\,\,;\,\,AH = 4\)
- D \({\rm{b)}}\,\,\angle B = {60^0}\,\,;\,\,\angle C = {30^0}\,\,;\,\,AH = 2\sqrt 3 \)
Đáp án: D
Phương pháp giải:
a) Áp dụng định lý Pitago đảo để chứng minh tam giác \(ABC\) vuông.
b) Sử dụng tỉ số lượng giác của góc nhọn và hệ thức lượng trong tam giác vuông để làm bài toán.
Lời giải chi tiết:
a) Chứng minh tam giác \(ABC\) vuông.
Ta có: \(A{B^2} = {4^2} = 16;\,\,A{C^2} = {\left( {4\sqrt 3 } \right)^2} = 48;\,\,B{C^2} = {8^2} = 64.\)
\( \Rightarrow A{B^2} + A{C^2} = 16 + 48 = 64 = B{C^2}\)
\( \Rightarrow \Delta ABC\) vuông tại \(A\) (định lý Pitago đảo).
b) Tính số đo \(\angle B,\,\,\angle C\) và độ dài đường cao \(AH\) của \(\Delta ABC.\)
Áp dụng tỉ số lượng giác của góc nhọn trong \(\Delta ABC\) ta có:
\(\begin{array}{l}\cos \angle B = \frac{{AB}}{{BC}} = \frac{4}{8} = \frac{1}{2} \Rightarrow \angle B = {60^0}\\ \Rightarrow \angle C = {180^0} - \angle B - \angle A = {180^0} - {60^0} - {90^0} = {30^0}.\end{array}\)
Áp dụng hệ thức lượng trong \(\Delta ABC\) vuông tại\(A\) và có đường cao \(AH\) ta có:
\(AH.BC = AB.AC \Rightarrow AH = \frac{{AB.AC}}{{BC}} = \frac{{4.4\sqrt 3 }}{8} = 2\sqrt 3 \,\,cm.\)
Vậy \(\angle B = {60^0},\,\,\,\angle C = {30^0},\,\,\,AH = 2\sqrt 3 \,\,cm.\)
Chọn D.
Câu hỏi 22 :
Cho \(\Delta MNP\) vuông tại\(M\) có đường cao \(MH.\) Gọi \(I,\,\,K\) lần lượt là hình chiếu vuông góc của \(H\) trên \(MN,\,\,MP.\) Biết \(HK = 9\,cm,\,\,\,HI = 6\,cm.\) Khi đó tính độ dài các cạnh của \(\Delta MNP.\)
- A \(MN = 12\,\,cm,\,\,MP = 19,5\,\,cm,\,\,\,NP = \frac{{3\sqrt {13} }}{2}\,\,cm.\)
- B \(MN = 13\,\,cm,\,\,MP = 19,5\,\,cm,\,\,\,NP = \frac{{3\sqrt {13} }}{2}\,\,cm.\)
- C \(MN = 13\,\,cm,\,\,MP = 17,5\,\,cm,\,\,\,NP = \frac{{3\sqrt {13} }}{2}\,\,cm.\)
- D \(MN = 13\,\,cm,\,\,MP = 19,5\,\,cm,\,\,\,NP = \frac{{5\sqrt {13} }}{2}\,\,cm.\)
Đáp án: B
Phương pháp giải:
Chứng minh tứ giác \(MKHI\) là hình chữ nhật từ đó ta tính được độ dài \(AH\) theo định lý Pitago.
Sử dụng các công thức hệ thức lượng trong tam giác vuông điểm tìm các cạnh đề bài yêu cầu.
Lời giải chi tiết:
Xét tứ giác \(MIHK\) ta có: \(\angle M = \angle I = \angle K = {90^0}\)
\( \Rightarrow MIHK\) là hình chữ nhật (dhnb).
\( \Rightarrow HI = MK = 6\,cm.\)
Áp dụng định lý Pitago cho \(\Delta MHK\) vuông tại \(K\) ta có:
\(M{H^2} = H{K^2} + M{K^2} = {6^2} + {9^2} = 117 \Rightarrow MH = \sqrt {117} .\)
Áp dụng hệ thức lượng trong \(\Delta MHP\) vuông tại \(H\) có đường cao \(HK\) ta có:
\(M{H^2} = MK.MP \Rightarrow MP = \frac{{M{H^2}}}{{MK}} = \frac{{117}}{6} = 19,5\,cm.\)
Áp dụng hệ thức lượng trong \(\Delta MHN\) vuông tại \(H\) có đường cao \(HI\) ta có:
\(M{H^2} = MI.MN \Rightarrow MN = \frac{{M{H^2}}}{{MI}} = \frac{{117}}{9} = 13\,cm.\)
Áp dụng định lý Pitago cho \(\Delta MNP\) vuông tại \(N\) ta có:
\(NP = \sqrt {M{N^2} + M{P^2}} = \sqrt {{{13}^2} + 19,{5^2}} = \frac{{13\sqrt {13} }}{2}\,\,cm.\)
Vậy\(MN = 13\,\,cm,\,\,MP = 19,5\,\,cm,\,\,NP = \frac{{13\sqrt {13} }}{2}\,\,cm.\)
Câu hỏi 23 :
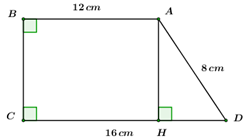
Cho hình thang vuông \(ABCD\) có hai đáy \(AB = 12\,cm,\,\,DC = 16\,\,cm,\) cạnh xiên \(AD = 8\,cm.\) Tính các góc và cạnh góc vuông của hình thang.
- A \(\begin{array}{l}
BC = 3\sqrt 3 \,\,cm\\
\angle A = {120^0},\,\,\angle D = {60^0}
\end{array}\) - B \(\begin{array}{l}
BC = 4\sqrt 3 \,\,cm\\
\angle A = {120^0},\,\,\angle D = {60^0}
\end{array}\) - C \(\begin{array}{l}
BC = 3\sqrt 3 \,\,cm\\
\angle A = {135^0},\,\,\angle D = {45^0}
\end{array}\) - D \(\begin{array}{l}
BC = 4\sqrt 3 \,\,cm\\
\angle A = {135^0},\,\,\angle D = {45^0}
\end{array}\)
Đáp án: D
Phương pháp giải:
Kẻ \(AH \bot CD = \left\{ H \right\},\,\,H \in CD.\)
Sử dụng tính chất hình thang vuông, hình chữ nhật; định lý Pitago và hệ thức lượng giác trong tam giác vuông để tính.
Lời giải chi tiết:
Kẻ \(AH \bot CD = \left\{ H \right\},\,\,H \in CD.\)
Có hình thang vuông \(ABCD\) cạnh xiên \(AD \Rightarrow \angle ABC = \angle BCD = {90^o}.\)
Dễ thấy \(ABCH\) là hình chữ nhật (có 3 góc vuông) \( \Rightarrow HC = AB = 12\,cm\)
\( \Rightarrow HD = DC - HC = 16 - 12 = 4\,\,(cm)\)
Áp dụng định lý Pitago cho \(\Delta AHD\) vuông tại \(H\) ta có:
\(\begin{array}{l}A{H^2} = A{D^2} - H{D^2} \Rightarrow AH = \sqrt {A{D^2} - H{D^2}} = \sqrt {{8^2} - {4^2}} = 4\sqrt 3 \,\,\left( {cm} \right).\\ \Rightarrow BC = AH \approx 6,93\,\,cm\end{array}\)
Xét \(\Delta AHD\) vuông tại \(H\) ta có: \(\cos \angle D = \frac{{HD}}{{AD}} = \frac{1}{2} \Rightarrow \angle D = {60^o}\)
\(\begin{array}{l} \Rightarrow \angle DAH = {90^o} - \angle D = {30^o}\\ \Rightarrow \angle BAD = \angle BAH + \angle DAH = {90^o} + {30^o} = {120^o}.\end{array}\)
Câu hỏi 24 :
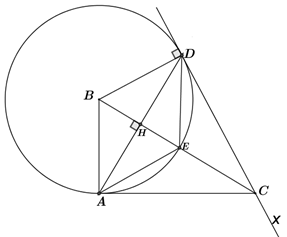
Cho hình vuông \(ABCD.\) Gọi \(I\) là một điểm nằm giữa \(A\) và \(B.\) Tia \(DI\) và tia \(CB\) cắt nhau ở \(K.\) Kẻ đường thẳng qua \(D,\) vuông góc với \(DI,\) cắt đường thẳng \(BC\) tại \(L.\) Chứng minh rằng :
a) \(\Delta DIL\) là một tam giác cân.
b) Tổng \(\frac{1}{{D{I^2}}} + \frac{1}{{D{K^2}}}\) không đổi khi \(I\) thay đổi trên cạnh \(AB.\)
Phương pháp giải:
a) Chứng minh \(DI = DL\) dựa vào \(\Delta DAI = \Delta DCL.\)
b) Áp dụng hệ thức lượng trong \(\Delta DLK\) vuông tại \(D,\) đường cao \(DC\) để chứng minh.
Lời giải chi tiết:
a) Xét \(\Delta DAI\) và \(\Delta DCL\) có:
\(DA = DC\) (\(ABCD\) là hình vuông);
\(\angle ADI = \angle CDL\) (cùng phụ với \(\angle CDI\))
\(\angle DAI = \angle DCL = {90^o}\)
\( \Rightarrow \Delta DAI = \Delta DCL\,\,\,\left( {c - g - c} \right) \Rightarrow DI = DL\) (2 cạnh tương ứng)
\( \Rightarrow \Delta DIL\) là tam giác cân tại \(D.\)
b) Áp dụng hệ thức lượng trong \(\Delta DLK\) vuông tại \(D,\) đường cao \(DC\) ta có:
\(\frac{1}{{D{I^2}}} + \frac{1}{{D{K^2}}} = \frac{1}{{D{L^2}}} + \frac{1}{{D{K^2}}} = \frac{1}{{D{C^2}}}\) không đổi.
Câu hỏi 25 :
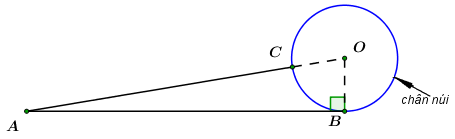
Có một vụ tai nạn ở vị trí B tại chân của một ngọn núi (chân núi có dạng đường tròn tâm O, bán kính 3km) và một trạm cứu hộ ở vị trí A (tham khảo hình vẽ). Do chưa biết đi đường nào để đến vị trí tai nạn nhanh hơn nên đội cứu hộ quyết định điều hai xe cứu thương cùng xuất phát ở trạm cứu hộ đến vị trí tai nạn theo hai cách sau:
Xe thứ nhất: đi theo đường thẳng từ A đến B, do đường xấu nên vận tốc trung bình của xe là 40 km/h.
Xe thứ hai: đi theo đường thẳng từ A đến C với vận tốc trung bình 60 km/h, rồi đi từ C đến B theo đường cung nhỏ CB ở chân núi với vận tốc trung bình 30 km/h (ba điểm A, O, C thẳng hàng và C ở chân núi). Biết đoạn đường AC dài 27 km và \(\angle ABO = {90^0}.\)
Câu 1:
Tính độ dài quãng đường xe thứ nhất đi từ A đến B.
- A \(AB \approx 25,85\,\,\,km.\)
- B \(AB \approx 29,85\,\,\,km.\)
- C \(AB \approx 25,65\,\,\,km.\)
- D \(AB \approx 29,65\,\,\,km.\)
Đáp án: B
Phương pháp giải:
Sử dụng định lý Pytago để tính độ dài quãng đường AB.
Lời giải chi tiết:
Ta có: \(AO = CA + OC = 27 + 3 = 30\,\,km.\)
Áp dụng định lý Pitago cho \(\Delta ABO\) vuông tại \(B\) ta có:
\(\begin{array}{l}A{B^2} = A{O^2} - O{B^2} = {30^2} - {3^2} = 891\\ \Rightarrow AB = \sqrt {891} = 9\sqrt {11} \approx 29,85\,\,km.\end{array}\)
Vậy quãng đường xe thứ nhất đi là \(AB \approx 29,85\,\,\,km.\)
Chọn B.
Câu 2:
Nếu hai xe cứu thương xuất phát cùng lúc tại A thì xe nào đến vị trí tai nạn trước?
- A Xe thứ nhất
- B Xe thứ hai
- C Hai xe đến cùng lúc
Đáp án: B
Phương pháp giải:
Sử dụng công thức tính độ dài cung tròn \({n^0}\) là: \(l = \frac{{\pi R{n^0}}}{{{{180}^0}}}\) để tính quãng đường xe thứ hai đi.
Tính thời gian hai xe đi để đến vị trí tai nạn rồi kết luận.
Lời giải chi tiết:
+) Thời gian xe thứ nhất đi đến vị trí tai nạn là: \(9\sqrt {11} :40 = \frac{{9\sqrt {11} }}{{40}} \approx 0,746\) giờ.
+) Ta có: \(\cos \angle AOB = \cos \angle COB = \frac{3}{{30}} = \frac{1}{{10}} \Rightarrow \angle COB \approx 84,{26^0}\)
\( \Rightarrow sd\,\,cung\,\,BC = \angle COB = 84,{26^0}\) (số đo góc ở tâm bằng số đo cung bị chắn).
\( \Rightarrow \) Độ dài cung \(BC\) là: \({l_{BC}} = \frac{{\pi .3.84,26}}{{180}} \approx 4,41\,\,km.\)
\( \Rightarrow \) Thời gian xe thứ hai đi đến vị trí tai nạn là: \(27:60 + 4,41:30 = 0,597\) giờ.
Ta thấy thời gian xe thứ hai đi đến vị trí tai nạn ít hơn thời gian xe thứ nhất đi đến vị trí tai nạn nên khi hai xe cùng xuất phát thì xe thứ hai đến trước xe thứ nhất.
Chọn B.
Câu hỏi 26 :
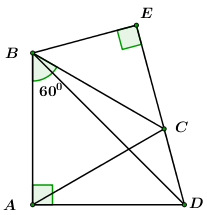
Cho tứ giác \(ABCD\) có \(AB = AC = AD = 20\,\,cm,\,\,\angle B = {60^0}\) và \(\angle A = {90^0}.\) Kẻ \(BE \bot DC\) kéo dài.
Câu 1:
Tính \(BE\)?
- A \(BE = 10\sqrt 2 \,\,cm\)
- B \(BE = 10\,\,cm\)
- C \(BE = 10\sqrt 3 \,\,cm\)
- D \(BE = 20 \,\,cm\)
Đáp án: A
Phương pháp giải:
Áp dụng định lý Pitago và các tỉ số lượng giác của góc nhọn để làm bài toán.
Lời giải chi tiết:
Áp dụng định lý Pitago cho \(\Delta ABD\) vuông tại \(A\) ta có:
\(DB = \sqrt {A{B^2} + A{D^2}} = \sqrt {{{20}^2} + {{20}^2}} = 20\sqrt 2 \,\,cm.\)
Mà \(\Delta ABD\) có \(AB = AD = 20\,cm \Rightarrow \Delta ABD\) vuông cân tại\(A.\)
\( \Rightarrow \angle ABD = \angle ADB = {45^0}\) (tính chất tam giác cân).
Theo đề bài ta có: \(\left\{ \begin{array}{l}AB = AC = 20\,cm\\\angle ABC = {60^0}\end{array} \right. \Rightarrow \Delta ABC\) là tam giác đều.
\( \Rightarrow BC = 20\,cm;\,\,\,\angle BAC = \angle BCA = {60^0}.\)
Lại có: \(AC = AD = 20\,\,cm \Rightarrow \Delta ACD\) cân tại \(A\)
\(\begin{array}{l} \Rightarrow \angle ACD = \angle ADC = \frac{{{{180}^0} - \angle CAD}}{2} = \frac{{{{180}^0} - \left( {{{90}^0} - \angle BAC} \right)}}{2} = \frac{{{{180}^0} - \left( {{{90}^0} - {{60}^0}} \right)}}{2} = {75^0}.\\ \Rightarrow \angle EDB = \angle ADC - \angle ADB = {75^0} - {45^0} = {30^0}.\end{array}\)
Xét \(\Delta BED\) vuông tại \(E\) ta có:
\(\left\{ \begin{array}{l}BE = BD.\sin \angle EDB = 20\sqrt 2 .\sin {30^0} = 20\sqrt 2 .\frac{1}{2} = 10\sqrt 2 \,\,cm.\\ED = BD.cos\angle EDB = 20\sqrt 2 .cos{30^0} = 20\sqrt 2 .\frac{{\sqrt 3 }}{2} = 10\sqrt 6 \,\,cm.\end{array} \right.\)
Câu 2:
Tính \(CE.\)?
- A \(CE=10cm\)
- B \(CE \approx 10,35\,\,cm\)
- C \(CE = 10\sqrt 3 \,\,cm\)
- D \(CE = 10\sqrt 2 \,\,cm\)
Đáp án: D
Phương pháp giải:
Áp dụng định lý Pitago và các tỉ số lượng giác của góc nhọn để làm bài toán.
Lời giải chi tiết:
Áp dụng định lý Pitago cho\(\Delta BEC\) vuông tại \(E\) ta có:
\(\begin{array}{l}EC = \sqrt {B{C^2} - B{E^2}} = \sqrt {{{20}^2} - {{\left( {10\sqrt 2 } \right)}^2}} = 10\sqrt 2 \,\,cm.\end{array}\)
Câu 3:
Tính \(CD\)?
- A \(CD = 10\sqrt 3 \,\,cm\)
- B \(CD=10cm\)
- C \(CD \approx 10,35\,\,cm\)
- D \(CD=20cm\)
Đáp án: C
Phương pháp giải:
Áp dụng định lý Pitago và các tỉ số lượng giác của góc nhọn để làm bài toán.
Lời giải chi tiết:
Ta có: \( CD = ED - EC = 10\sqrt 6 - 10\sqrt 2 = 10\sqrt 2 \left( {\sqrt 3 - 1} \right)\,\,\,cm \approx 10,35\,\,cm\)
Câu hỏi 27 :
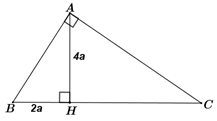
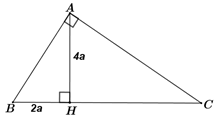
Cho tam giác \(ABC\) vuông tại \(A\) có đường cao \(AH = 4a,\, \, HB = 2a\) với \(0 < a \in \mathbb{R}.\)
Câu 1:
Tính \(HC\) theo \(a.\)
- A \(HC = 5a\)
- B \(HC = 6a\)
- C \(HC = 7a\)
- D \(HC = 8a\)
Đáp án: D
Phương pháp giải:
Áp dụng hệ thức lượng trong tam giác vuông và công thức tính tan của 1 góc.
Lời giải chi tiết:
Tính \(HC\) theo \(a.\)
Áp dụng hệ thức lương trong \(\Delta ABC\)vuông tại \(A\) có đường cao \(AH\) ta có:
\(A{H^2} = HB.HC \Rightarrow HC = \frac{{A{H^2}}}{{HB}} = \frac{{{{\left( {4a} \right)}^2}}}{{2a}} = \frac{{16{a^2}}}{{2a}} = 8a\)
Vậy \(HC = 8a.\)
Câu 2:
Tính \(\tan \angle ABC.\)
- A \(2\)
- B \(1\)
- C \(\sqrt 3 \)
- D \(\frac{{\sqrt 3 }}{3}\)
Đáp án: A
Phương pháp giải:
Áp dụng hệ thức lượng trong tam giác vuông và công thức tính tan của 1 góc.
Lời giải chi tiết:
Tính \(\tan \angle ABC.\)
Xét \(\Delta ABH\) vuông tại \(H\) ta có: \(\tan \angle ABC = \frac{{AH}}{{HB}} = \frac{{4a}}{{2a}} = 2.\)
Chọn A.
Câu hỏi 28 :
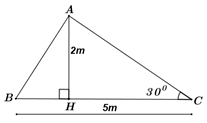
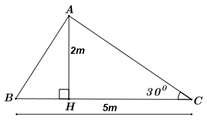
Để lợp một mái nhà bằng tôn, thợ sắt hàn khung sắt hình tam giác \(ABC\) (xem hình vẽ), biết một kích thước của khung sắt là \(BC = 5m\), chiều cao khung sắt là \(AH = 2m\) và độ dốc mái tôn phía sau là \(\angle ACB = {30^0}\). Tìm độ dài \(AB\) của khung sắt phía trước.
(Kết quả cuối cùng làm tròn đến 2 chữ số thập phân).
- A \(AB = 3,42\,m\)
- B \(AB = 3,64\,m\)
- C \(AB = 2,85\,m\)
- D \(AB = 2,52\,m\)
Đáp án: D
Phương pháp giải:
Sử dụng công thức tính tan 1 góc để tính cạnh \(AH\) và định lý Pytago trong \(\Delta ABH\)vuông tại \(H\) để tính cạnh \(AB.\)
Lời giải chi tiết:
Xét \(\Delta AHC\)vuông tại \(H\) ta có: \(\begin{array}{l}\tan C = \frac{{AH}}{{CH}} \Rightarrow \tan {30^0} = \frac{2}{{CH}} \Rightarrow CH = \frac{2}{{\tan {{30}^0}}} = 2\sqrt 3 \left( m \right)\\ \Rightarrow BH = BC - CH = 5 - 2\sqrt 3 \,\,\left( m \right)\end{array}\)
Xét \(\Delta ABH\) vuông tại \(H,\) theo định lý Pytago ta có:
\(\begin{array}{l}A{B^2} = A{H^2} + B{H^2} = {2^2} + {\left( {5 - 2\sqrt 3 } \right)^2} = 41 - 20\sqrt 3 \\ \Rightarrow AB = \sqrt {41 - 20\sqrt 3 } \simeq 2,52\left( m \right)\end{array}\)
Vậy \(AB = 2,52\,m\).
Chọn D.
Câu hỏi 29 :
Cho tam giác \(ABC\) có \(AH\) là đường cao, biết \(BH = 9\,cm,HC = 16\,\,cm\) và \({\rm{tan }}\angle ACB = \frac{3}{4}.\)
a) Tính độ dài các cạnh \(AH,\,\,AC.\)
b) Vẽ đường tròn tâm \(B\) bán kính \(BA.\) Chứng minh rằng \(AC\) là tiếp tuyến của đường tròn \(\left( {B;BA} \right)\).
c) Tia \(AH\) cắt đường tròn \(\left( {B;BA} \right)\) tại \(D\,\,\,\left( {D \ne A} \right).\) Vẽ tiếp tuyến \(Dx\) của \(\left( {B;BA} \right)\) (với \(D\) là tiếp điểm). Chứng minh rằng \(Dx\) đi qua điểm \(C.\)
d) Cạnh \(BC\) cắt đường tròn \(\left( {B;BA} \right)\) tại \(E.\)
Chứng minh: \(AE\) là tia phân giác của góc \(HAC\) và \(EH.\tan \,ABC = EC.\sin \,ABC\).
Phương pháp giải:
a) Áp dụng công thưc tính tan 1 góc và định lý Pytago trong tam giác vuông.
b) Chứng minh \(\Delta ABC\) vuông tại \(A\) qua định lý Pytago đảo, suy ra \(BA \bot CA.\)
c) Chứng minh \(\Delta ABC = \Delta DBC\) để suy ra \(DC\) là tiếp tuyến của đường tròn \(\left( {B;BA} \right),\,\,DC \equiv Dx.\)
d) Chứng minh \(\angle EAC = \angle HAE\)do cùng phụ với \(\angle BEA\)
+) Biến đổi tương đương biểu thức cần chứng minh về 1 kết quả luôn đúng.
Lời giải chi tiết:
a) Tính độ dài các cạnh \(AH,\,\,AC.\)
Trong \(\Delta AHC\)vuông tại \(H\) có:
\(\tan ACB = \frac{{AH}}{{HC}} = \frac{3}{4} \Rightarrow AH = HC.\frac{3}{4} = 16.\frac{3}{4} = 12\,\,\,\left( {cm} \right).\)
\(A{C^2} = A{H^2} + H{C^2} = {12^2} + {16^2} = 400 \Rightarrow AC = \sqrt {400} = 20\,\,\,\left( {cm} \right).\)
Vậy \(AH = 12\,\,cm;\,\,\,AC = 20\,\,cm.\)
b) Vẽ đường tròn tâm \(B\) bán kính \(BA.\) Chứng minh rằng \(AC\) là tiếp tuyến của đường tròn \(\left( {B;BA} \right)\).
Trong \(\Delta ABH\)vuông tại \(H\) có: \(AB = \sqrt {A{H^2} + B{H^2}} = \sqrt {{{12}^2} + {9^2}} = \sqrt {225} = 15\,\,\left( {cm} \right).\)
Nhận thấy: \(A{B^2} + A{C^2} = {15^2} + {20^2} = 625 = {25^2} = B{C^2}\)
\( \Rightarrow \Delta ABC\)vuông tại \(A \Rightarrow BA \bot CA.\)
\( \Rightarrow AC\) là tiếp tuyến của đường tròn \(\left( {B;BA} \right)\) (định nghĩa).
Vậy \(AC\) là tiếp tuyến của đường tròn \(\left( {B;BA} \right)\).
c) Tia \(AH\) cắt đường tròn \(\left( {B;BA} \right)\) tại \(D\,\,\,\left( {D \ne A} \right).\) Vẽ tiếp tuyến \(Dx\) của \(\left( {B;BA} \right)\) (với \(D\) là tiếp điểm). Chứng minh rằng \(Dx\) đi qua điểm \(C.\)
+) Xét \(\Delta ABD\)có: \(BA = BD\); \(BH \bot AD\)
\( \Rightarrow BH\) là đường cao đồng thời là đường phân giác của \(\Delta ABD\)cân tại \(B\) (tính chất).
\( \Rightarrow \angle ABC = \angle DBC\)
+) Xét \(\Delta ABC\)và \(\Delta DBC\)có:
\(\begin{array}{l}BC\,\,chung\\\angle ABC = \angle DBC\,\,\,\left( {cmt} \right)\\BA = BD\,\,\,\left( {gt} \right)\\ \Rightarrow \Delta ABC = \Delta DBC\,\,\,\left( {c - g - c} \right).\end{array}\)
\( \Rightarrow \angle BAC = \angle BDC = {90^0}\) (hai góc tương ứng).
\( \Rightarrow BD \bot DC\)
\( \Rightarrow DC\)là tiếp tuyến của đường tròn \(\left( {B;BA} \right)\).
\( \Rightarrow DC \equiv Dx\) hay \(Dx\) đi qua điểm \(C\) (đpcm).
d) Cạnh \(BC\) cắt đường tròn \(\left( {B;BA} \right)\) tại \(E.\)
Chứng minh: \(AE\) là tia phân giác của góc \(HAC\) và \(EH.\tan \,ABC = EC.\sin \,ABC\).
+) Ta có \(\angle BAE = \angle BEA\) (do \(\Delta ABE\) cân tại \(B\))
Lại có: \(\angle BAE + \angle EAC = \angle BAC = {90^0}\)
\( \Rightarrow \angle BEA + \angle EAC = {90^0}\)(1)
Mặt khác: \(\angle BEA + \angle HAE = {180^0} - \angle AHE = {90^0}\)(2)
Từ (1) và (2) \( \Rightarrow \angle EAC = \angle HAE \Rightarrow AE\) là tia phân giác của \(\angle HAC\) (đpcm)
+) Nếu: \(EH.\tan \,ABC = EC.\sin \,ABC\)
Thì \(EH.\frac{{AC}}{{AB}} = EC.\frac{{AC}}{{BC}} \Rightarrow EH.\frac{{20}}{{15}} = EC.\frac{{20}}{{25}} \Rightarrow \frac{{EH}}{3} = \frac{{EC}}{5}\)(1)
Ta có: \(AE\) là tia phân giác của \(\angle HAC\)
\( \Rightarrow \frac{{EH}}{{EC}} = \frac{{AH}}{{AC}} = \frac{{12}}{{20}} = \frac{3}{5}\) (tính chất đường phân giác)
\( \Rightarrow \frac{{EH}}{3} = \frac{{EC}}{5}\)\( \Rightarrow \left( 1 \right)\) luôn đúng.
Vậy \(EH.\tan \,ABC = EC.\sin \,ABC\).
Câu hỏi 30 :
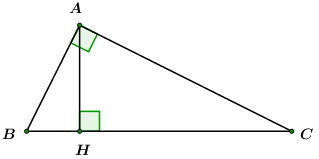
1) Cho tam giác \(ABC\) vuông tại \(A\) có \(AB = 3\,cm;\,AC = 4\,cm\). Kẻ đường cao \(AH\,\,\,\left( {H \in BC} \right).\) Tính \(BH,\,\,CH.\)
2) Cho tam giác \(ABC\) có \(AB = 3,6\,cm;\,\,AC = 4,8\,cm;\,\,\,BC = 6\,cm.\) Tính các góc \(B,\,\,C\) (viết kết quả dạng độ, phút, giây) và đường cao \(AH\) của tam giác \(ABC.\)
Phương pháp giải:
1) Áp dụng hệ thức lượng tròn tam giác vuông.
2) Chứng minh tam giác ABC vuông tại A qua định lý Pytago đảo; tính các góc B,C qua sin của chúng; tính AH qua hệ thức lượng trong tam giác.
Lời giải chi tiết:
1) Cho tam giác \(ABC\) vuông tại \(A\) có \(AB = 3\,cm;\,AC = 4\,cm\). Kẻ đường cao \(AH\,\,\,\left( {H \in BC} \right).\) Tính \(BH,\,\,CH.\)
+) Tam giác ABC vuông tại A nên theo định lý Pytago ta có:
\(B{C^2} = A{B^2} + A{C^2} = {3^2} + {4^2} = 25 \Rightarrow BC = \sqrt {25} = 5\left( {cm} \right)\)
+) Theo hệ thức lượng trong tam giác vuông ta có:
\(A{B^2} = BH.BC \Rightarrow BH = \frac{{A{B^2}}}{{BC}} = \frac{{{3^2}}}{5} = \frac{9}{5} = 1,8\left( {cm} \right)\)
\( \Rightarrow CH = BC - BH = 5 - 1,8 = 3,2\left( {cm} \right)\)
Vậy \(BH = 1,8cm;\,CH = 3,2cm\)
2) Cho tam giác \(ABC\) có \(AB = 3,6\,cm;\,\,AC = 4,8\,cm;\,\,\,BC = 6\,cm.\) Tính các góc \(B,\,\,C\) (viết kết quả dạng độ, phút, giây) và đường cao \(AH\) của tam giác \(ABC.\)
+)Ta thấy \(A{B^2} + A{C^2} = 3,{6^2} + 4,{8^2} = 36 = {6^2} = B{C^2}\)
\( \Rightarrow \Delta ABC\)vuông tại A (theo định lý Pytago đảo)
+) \(\sin \widehat B = \frac{{AC}}{{BC}} = \frac{{4,8}}{6} = \frac{4}{5} \Rightarrow \widehat B = {53^0}7'48,37''\)
+) \(\sin \widehat C = \frac{{AB}}{{BC}} = \frac{{3,6}}{6} = \frac{3}{5} \Rightarrow \widehat C = {36^0}52'11,63''\)
+) Theo hệ thức lượng ta có: \(AH.BC = AB.AC \Rightarrow AH = \frac{{AB.AC}}{{BC}} = \frac{{3,6.4,8}}{6} = 2,88\left( {cm} \right)\)
Câu hỏi 31 :
Tam giác \(ABC\)có \(\angle C - \angle B = 90^\circ ,\) \(AH\) là đường cao của tam giác. Chứng minh rằng \(A{H^2} = BH.CH\)
Phương pháp giải:
- Sử dụng tính chất góc ngoài của tam giác.
- Sử dụng tam giác đồng dạng và suy ra các cạnh tương ứng tỉ lệ.
Lời giải chi tiết:

Ta có: \(\angle ACB - \angle B = 90^\circ \)\( \Rightarrow \angle ACB > {90^0}\)\( \Rightarrow \angle ACB\) là góc tù.
\( \Rightarrow \angle B = \angle ACB - {90^0}\).
Mặt khác: \(\angle ACB = \angle HAC + \angle AHC = \angle HAC + {90^0}\) (góc ngoài của tam giác).
\( \Rightarrow \angle HAC = \angle ACB - {90^0}.\)
Do đó: \(\angle HAC = \angle B\).
Xét \(\Delta AHC\) và \(\Delta BHA\) có:
\(\angle H\) chung;
\(\angle HAC = \angle B\,\,\left( {cmt} \right)\);
\( \Rightarrow \Delta AHC\)đồng dạng với\(\Delta BHA\) (g.g).
\( \Rightarrow \dfrac{{AH}}{{BH}} = \dfrac{{CH}}{{AH}} \Leftrightarrow A{H^2} = BH.CH.\)
Câu hỏi 32 :
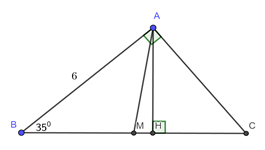
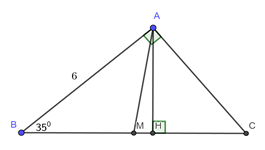
Cho tam giác \(ABC\) vuông tại \(A\),\(\angle B = {35^0}\)và \(AB{\rm{ }} = {\rm{ 6}}cm\)
Câu 1:
Giải tam giác vuông \(ABC\).
- A \(AC = 8,57cm\,\,;\,\,BC = 10,46cm\,\,;\,\,\angle C = {55^0}\)
- B \(AC = 4,9cm\,\,;\,\,BC = 7,75cm\,\,;\,\,\angle C = {55^0}\)
- C \(AC = 4,2cm\,\,;\,\,BC = 7,32cm\,\,;\,\,\angle C = {55^0}\)
- D \(AC = 3,44cm\,\,;\,\,BC = 6,92cm\,\,;\,\,\angle C = {55^0}\)
Đáp án: C
Phương pháp giải:
Sử dụng công thức liên hệ giữa cạnh và góc trong tam giác vuông.
Sử dụng tính chất hai góc phụ nhau.
Sử dụng hệ thức lượng trong tam giác vuông.
Áp dụng công thức tính diện tích tam giác.
Lời giải chi tiết:
Xét \(\Delta ABC\) vuông tại \(A\) ta có:
\(AC = AB.tan\angle B = 6.tan{35^0} \approx 4,2\)
\(AB = BC.\cos \angle B \Rightarrow 6 = BC.\cos {35^0} \Rightarrow BC \approx 7,32\)
Vì \(\Delta ABC\) vuông tại \(A\) ta có:
\(\angle B + \angle C = {90^0} \Leftrightarrow {35^0} + \angle C = {90^0}\)\( \Leftrightarrow \angle C = {55^0}\)
Chọn C.
Câu 2:
Vẽ đường cao \(AH\) và trung tuyến \(AM\) của tam giác \(ABC\). Tính diện tích \(\Delta AHM\)
- A \({S_{\Delta AHM}} = 2,17\,\,\left( {dvdt} \right)\)
- B \({S_{\Delta AHM}} = 3,24\,\,\left( {dvdt} \right)\)
- C \({S_{\Delta AHM}} = 2,86\,\,\left( {dvdt} \right)\)
- D \({S_{\Delta AHM}} = 3,35\,\,\left( {dvdt} \right)\)
Đáp án: A
Phương pháp giải:
Sử dụng công thức liên hệ giữa cạnh và góc trong tam giác vuông.
Sử dụng tính chất hai góc phụ nhau.
Sử dụng hệ thức lượng trong tam giác vuông.
Áp dụng công thức tính diện tích tam giác.
Lời giải chi tiết:
Vì \(AM\)là trung tuyến của tam giác \(ABC \Rightarrow M\)là trung điểm \(BC\)\( \Rightarrow BM = MC = \frac{{BC}}{2} \approx 3,66\)
Áp dụng hệ thức lượng cho \(\Delta ABC\) vuông tại \(A,\) có đường cao \(AH\) ta có:
\(AH.BC = AB.AC\)\( \Leftrightarrow AH.7,32 = 6.4,2\)\( \Leftrightarrow AH \approx 3,44\)
\(A{B^2} = BH.CB\)\( \Leftrightarrow {6^2} = BH.7,32\)\( \Leftrightarrow BH \approx 4,92\)
Ta có: \(BM + MH = BH \Leftrightarrow MH = 4,92 - 3,66 \approx 1,26\)
\({S_{\Delta AHM}} = \frac{1}{2}AH.MH \approx \frac{1}{2}.3,44.1,26 \approx 2,17\,\,\,\left( {dvdt} \right)\)
Chọn A.
Câu hỏi 33 :
Cho tam giác \(ABC\) vuông tại \(A\), \(AB{\rm{ }} = {\rm{ 15}}cm;AC = 20cm\).
Câu 1:
Giải tam giác \(ABC\)
- A \(BC = 25\,\,;\,\,\angle B = {36^0}52'\,\,;\,\,\angle C = {53^0}8'\)
- B \(BC = 25\,\,;\,\,\angle B = {53^0}8'\,\,;\,\,\angle C = {36^0}52'\)
- C \(BC = 25\,\,;\,\,\angle B = {41^0}25'\,\,;\,\,\angle C = {48^0}35'\)
- D \(BC = 25\,\,;\,\,\angle B = {48^0}35'\,\,;\,\,\angle C = {41^0}25'\)
Đáp án: B
Phương pháp giải:
Sử dụng định lý Pi-ta-go, tỉ số lượng giác trong tam giác vuông.
Sử dụng tính chất tia phân giác.
Lời giải chi tiết:
Áp dụng định lý Pitago cho \(\Delta ABC\) vuông tại \(A\) có:
\(A{B^2} + A{C^2} = B{C^2}\) \( \Leftrightarrow B{C^2} = {15^2} + {20^2} = 625\)\( \Rightarrow BC = 25\)
Xét \(\Delta ABC\) vuông tại \(A\) ta có:
\(sinB = \frac{{AC}}{{BC}} = \frac{{20}}{{25}} \Rightarrow \angle B \approx {53^0}8'\)
Vì \(\Delta ABC\) vuông tại \(A\) ta có:
\(\angle B + \angle C = {90^0}\)\( \Leftrightarrow {53^0}8' + \angle C = {90^0}\)\( \Leftrightarrow \angle C \approx {36^0}52'\)
Chọn B.
Câu 2:
Phân giác của góc \(A\) cắt \(BC\) tại \(E\). Tính \(BE;CE\).
- A \(BE = \frac{{125}}{7}\,\,;\,\,CE = \frac{{100}}{7}\)
- B \(BE = \frac{{125}}{7}\,\,;\,\,CE = \frac{{75}}{7}\)
- C \(BE = \frac{{75}}{7}\,\,;\,\,CE = \frac{{100}}{7}\)
- D \(BE = \frac{{100}}{7}\,\,;\,\,CE = \frac{{125}}{7}\)
Đáp án: C
Phương pháp giải:
Sử dụng định lý Pi-ta-go, tỉ số lượng giác trong tam giác vuông.
Sử dụng tính chất tia phân giác.
Lời giải chi tiết:
Vì \(AE\) là tia phân giác góc \(A\) nên ta có:
\( \Rightarrow \frac{{BE}}{{AB}} = \frac{{EC}}{{AC}} = \frac{{BE + EC}}{{AB + AC}}\)\( = \frac{{BC}}{{AB + AC}} = \frac{{25}}{{15 + 20}} = \frac{5}{7}\)
\( \Rightarrow \left\{ \begin{array}{l}BE = \frac{5}{7}AB = \frac{5}{7}.15 = \frac{{75}}{7}\\EC = \frac{5}{7}AC = \frac{5}{7}.20 = \frac{{100}}{7}\end{array} \right..\)
Chọn C.
Câu hỏi 34 :
Một chiếc hộp hình hộp chữ nhật \(ABCD.ABCD\) có \(AB=12cm,BC=8cm,BB=5cm\), điểm \(E\) thuộc cạnh \(AB\) và \(EB=4cm\) . Chiếc hộp được đặt trên sàn. Một con kiến bò trên mặt chiếc hộp từ \(E\) đến \(C'\). Tính độ dài đoạn đường đi ngắn nhất của con kiến.
- A \(11cm\)
- B \(10cm\)
- C \(13,6cm\)
- D \(13cm\)
Đáp án: D
Phương pháp giải:
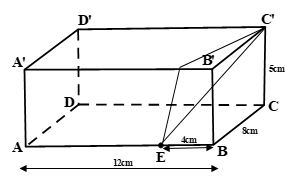
Phân tích bài toán:
Đây là một bài hình không gian, mang tính phân loại học sinh. Bài toán này đòi hỏi học sinh phải có khả năng tư duy tốt, biết chuyển đổi từ một hình không gian về một hình học phẳng. Có một số em hiểu sai đề bài và cho rằng con kiến sẽ đi theo các “mép” cạnh để tới điểm C’ nên cộng tổng độ dài các cạnh lại. Thực tế con kiến đi trên bề mặt của chiếc hộp chứ không phải bò trên các “mép” cạnh. Để dễ hiểu hơn các em cứ tượng tưởng mình có một chiếc hộp như trên. Sau đó, mình tháo ra và duỗi phẳng chiếc hộp để ra điểm C’’( thực ra là điểm C’, ghi như vậy để phân biệt) hoặc tháo hai bên “hông” của hộp để ra điểm C’. Rồi ta áp dụng định lý pitago để tính.
Lời giải chi tiết:
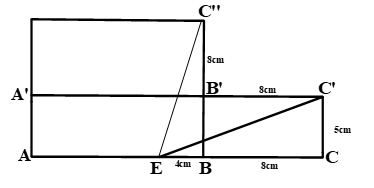
Điểm C’’ cũng chính là điểm C’ Con kiến có hai cách bò từ E đên C’
Cách 1: Vượt qua cạnh BB’
Đoạn đường đi ngắn nhất trong trường hợp này là
\(EC'=\sqrt{{{\left( EB+BC \right)}^{2}}+CC{{'}^{2}}}=\sqrt{{{\left( 4+8 \right)}^{2}}+{{5}^{2}}}=13cm\)
Cách 2: Vượt qua cạnh A’B’
Đoạn đường đi ngắn nhất trong trường hợp này là
\(EC' = \sqrt {{{\left( {BB' + B'C''} \right)}^2} + E{B^2}} = \sqrt {{{\left( {5 + 8} \right)}^2} + {4^2}} = \sqrt {185} cm\)
So sánh hai cách bò trên, đoạn đường đi ngắn nhất của con kiến là \(13cm\)
(Không xét con đường mà con kiến bò vượt qua cạnh AA’, vì con đường này rõ ràng dài hơn các con đường trên).
Câu hỏi 35 :
Cho \(\Delta ABC\) vuông tại \(A,\) đường cao \(AH.\) Gọi \(D\) là điểm đối xứng với \(A\) qua điểm \(B.\) Trên tia đối của \(HA\) lấy điểm \(E\) sao cho \(HE = 2HA.\) Gọi \(I\) là hình chiếu của \(D\) trên \(HE.\)
a) Tính độ dài \(AB,\,\,AC,\,\,HC\) biết \(AH = 4\,cm,\,\,BH = 3\,cm.\)
b) Tính \(\tan \angle IED,\,\,\tan \angle HCE.\)
c) Chứng minh \(\angle IED = \angle HCE.\)
d) Chứng minh \(DE \bot EC.\)
Phương pháp giải:
a) Sử dụng định lý Pitago và hệ thức lượng trong tam giác vuông để tính độ dài các cạnh.
b) Tính tỉ số lượng giác các góc nhọn trong tam giác vuông.
c) Chứng minh \(\tan \angle IED=\tan \angle HCE\Rightarrow \angle IED=\angle HCE.\)
d) Chứng minh \(\angle DEC = {90^0}.\)
Lời giải chi tiết:
a) Tính độ dài \(AB,\,\,AC,\,\,HC\) biết \(AH = 4\,cm,\,\,BH = 3\,cm.\)
Áp dụng định lý Pitago cho \(\Delta ABH\) vuông tại \(H\) ta có:
\(AB = \sqrt {A{H^2} + B{H^2}} = \sqrt {{4^2} + {3^3}} = 5\,\,cm.\)
Áp dụng hệ thức lượng trong \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH\) ta có:
\(\begin{array}{l}\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} \Leftrightarrow \frac{1}{{A{C^2}}} = \frac{1}{{A{H^2}}} - \frac{1}{{A{B^2}}}\\ \Leftrightarrow \frac{1}{{A{C^2}}} = \frac{1}{{{4^2}}} - \frac{1}{{{5^2}}} = \frac{9}{{400}} \Rightarrow AC = \frac{{20}}{3}\,\,cm.\\A{H^2} = BH.HC \Rightarrow HC = \frac{{A{H^2}}}{{BH}} = \frac{{{4^2}}}{3} = \frac{{16}}{3}\,\,cm.\end{array}\)
Vậy \(AB = 5cm,\,\,\,AC = \frac{{20}}{3}\,cm,\,\,\,HC = \frac{{16}}{3}\,cm.\)
b) Tính \(\tan \angle IED,\,\,\tan \angle HCE.\)
Ta có: \(\left\{ \begin{array}{l}AE \bot BC\\DI \bot AE\end{array} \right. \Rightarrow BC//DI\,\,\,hay\,\,\,BH//DI.\)
Xét \(\Delta AID\) ta có: \(B\) là trung điểm của \(AD\) và \(BH//DI\,\,\,\left( {cmt} \right)\)
\( \Rightarrow H\) là trung điểm của \(AI.\) (định lý đảo đường trung bình của tam giác)
Và \(BH = \frac{1}{2}DI \Rightarrow DI = 2BH = 2.3 = 6\,\,cm.\)
\( \Rightarrow AH = AI = IE = \frac{1}{3}AE = 5\,\,cm.\)
Xét \(\Delta DIE\) ta có: \(\tan \angle DEI = \frac{{DI}}{{IE}} = \frac{6}{4} = \frac{3}{2}.\)
Xét \(\Delta HCE\) ta có: \(\tan \angle HCE = \frac{{HE}}{{HC}} = \frac{{2AH}}{{HC}} = \frac{{2.4}}{{\frac{{16}}{3}}} = \frac{3}{2}.\)
Vậy \(\tan \angle DEI = \frac{3}{2};\,\,\,\tan \angle HCE = \frac{3}{2}.\)
c) Chứng minh \(\angle IED = \angle HCE.\)
Ta có: \(\tan \angle IED = \tan \angle HCE = \frac{3}{2} \Rightarrow \angle IED = \angle HCE\,\,\,\left( {dpcm} \right).\)
d) Chứng minh \(DE \bot EC.\)
Xét \(\Delta HEC\) ta có: \(\angle HEC + \angle HCE = {90^0}\)
Mà \(\angle DEI = \angle HCE\,\,\,\left( {cmt} \right)\)
\(\begin{array}{l} \Rightarrow \angle DEC = \angle CEI + HCE = {90^0}\\Hay\,\,\,DE \bot EC\,\,\,\left( {dpcm} \right).\end{array}\)
Câu hỏi 36 :
Cho \(\Delta ABC\) vuông tại \(A,\,\) đường cao \(AH.\) Cho \(\cos \angle ABC = \frac{3}{5}\) và \(BC = 10\,cm.\)
a) Tính độ dài các cạnh \(AC,\,\,HC\) và tính giá trị biểu thức: \(M = \frac{{2\cos B - 3\sin B}}{{1 + \tan B}}.\)
b) Từ \(C\) kẻ đường thẳng song song với \(AB,\) cắt \(AH\) tại \(D.\) Tính diện tích tứ giác \(ABDC.\)
Phương pháp giải:
a) Sử dụng hệ thức lượng trong tam giác vuông và tỉ số lượng giác của góc nhọn.
b) Chứng minh tứ giác \(ABDC\) là hình thang vuông sau đó sử dụng công thức tính diện tích hình thang.
Lời giải chi tiết:
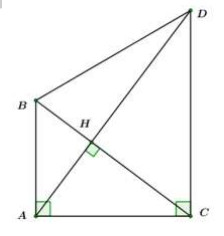
a) Tính độ dài các cạnh \(AC,\,\,HC\) và tính giá trị biểu thức: \(M = \frac{{2\cos B - 3\sin B}}{{1 + \tan B}}.\)
Xét \(\Delta ABC\) ta có: \(\cos \angle ABC = \frac{3}{5} = \frac{{AB}}{{BC}} \Rightarrow AB = \frac{3}{5}.10 = 6\,\,cm.\)
\(AC = \sqrt {B{C^2} - A{B^2}} = \sqrt {{{10}^2} - {6^2}} = 8\,\,cm.\)
Áp dụng hệ thức lượng trong \(\Delta ABC\) vuông tại\(A\) có đường cao \(AH\) ta có:
\(A{C^2} = HC.BC \Rightarrow HC = \frac{{A{C^2}}}{{BC}} = \frac{{{8^2}}}{{10}} = 6,4\,\,cm.\)
Xét \(\Delta ABC\) ta có:
\(\begin{array}{l}\sin \angle B = \frac{{AC}}{{BC}} = \frac{8}{{10}} = \frac{4}{5};\,\,\,\,\,\tan \angle B = \frac{{AC}}{{AB}} = \frac{8}{6} = \frac{4}{3}\\ \Rightarrow M = \frac{{2\cos B - 3\sin B}}{{1 + \tan B}} = \frac{{2.\frac{3}{5} - 3.\frac{4}{5}}}{{1 + \frac{4}{3}}} = - \frac{{18}}{{35}}.\end{array}\)
b) Từ \(C\) kẻ đường thẳng song song với \(AB,\) cắt \(AH\) tại \(D.\) Tính diện tích tứ giác \(ABDC.\)
Ta có:\(\left\{ \begin{array}{l}AB \bot AC\,\,\left( {gt} \right)\\CD \bot AC\,\,\left( {gt} \right)\end{array} \right. \Rightarrow AB//CD \Rightarrow ABDC\) là hình thang vuông tại \(A,\,\,C.\)
Áp dụng hệ thức lượng trong \(\Delta ACD\) vuông tại \(C\) có đường cao \(CH\) là:
\(\begin{array}{l}\frac{1}{{C{D^2}}} = \frac{1}{{C{H^2}}} - \frac{1}{{C{A^2}}} = \frac{1}{{6,{4^2}}} - \frac{1}{{{8^2}}} = \frac{9}{{1024}}\\ \Rightarrow C{D^2} = \frac{{1024}}{9} \Rightarrow CD = \frac{{32}}{3}\,\,\,cm.\end{array}\)
Ta có diện tích hình thang \(ABDC\) là: \(S = \frac{{\left( {AB + CD} \right).AC}}{2} = \frac{{\left( {6 + \frac{{32}}{3}} \right).8}}{2} = \frac{{200}}{3}\,\,\,c{m^2}.\)
Câu hỏi 37 :
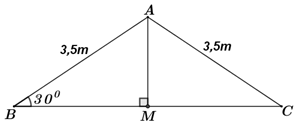
Bạn An đang học vẽ hình bằng phần mềm máy tính. An vẽ hình một ngôi nhà với phần mái có dạng hình tam giác cân (hình vẽ bên). Biết góc tạo bởi phần mái và mặt phẳng nằm ngang là \({30^0}\), chiều dài mỗi bên dốc mái là \(3,5\,\,m.\) Tính gần đúng bề rộng của mái nhà.
- A \(6,52\,m.\)
- B \(6,06\,m.\)
- C \(5,86\,m.\)
- D \(5,38\,m.\)
Đáp án: B
Phương pháp giải:
Áp dụng phương pháp tính cạnh trong tam giác vuông khi biết 1 góc và cạnh huyền.
Lời giải chi tiết:
Ta vẽ lại mô hình mái nhà như hình vẽ bên.
Theo đề bài cho ta có: \(\Delta ABC\) cân tại \(A\)
\(AB = AC = 3,5m\) và \(\angle B = \angle C = {30^0}\)
Thì khi đó bề rộng mái nhà chính là độ dài cạnh \(BC.\)
Gọi \(M\) là trung điểm của \(BC.\)
\( \Rightarrow AM\) là đường trung tuyến đồng thời là đường cao của \(\Delta ABC\) (tính chất).
Xét \(\Delta ABM\) vuông tại \(M\) ta có:
\(\cos B = \frac{{BM}}{{AB}} \Rightarrow cos\,{30^0} = \frac{{BM}}{{3,5}} \Rightarrow BM = \cos \,{30^0}.3,5 = \frac{{\sqrt 3 }}{2}.3,5 = \frac{{7\sqrt 3 }}{4}\,\,\,\left( m \right).\)
\( \Rightarrow BC = 2BM\frac{{7\sqrt 3 }}{2}\,\,\left( m \right) \approx 6,06\,\,m.\)
Vậy bề rộng mái nhà là \(6,06\,m.\)
Chọn B.
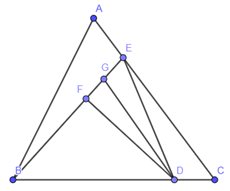
Câu hỏi 38 :
Cho tam giác \(ABC\) có diện tích là \(900\,c{m^2}.\) Điểm \(D\) ở giữa \(BC\) sao cho \(BC = 5DC,\) điểm \(E\) ở giữa \(AC\) sao cho \(AC = 4AE,\) hai điểm \(F,G\) ở giữa \(BE\) sao cho \(BE = 6GF = 6GE.\) Tính diện tích tam giác \(DGF.\)
- A \(80cm^2\)
- B \(90cm^2\)
- C \(100cm^2\)
- D \(120cm^2\)
Đáp án: B
Phương pháp giải:
Sử dụng tỉ số diện tích giữa hai tam giác.
Lời giải chi tiết:
Ta có: \(\left\{ \begin{array}{l}{S_{\Delta DFG}} = \frac{1}{2}d\left( {D;\,\,FG} \right).FG\\{S_{\Delta DEB}} = \frac{1}{2}d\left( {D;\,\,FG} \right).BE\end{array} \right. \Rightarrow \frac{{{S_{\Delta DFG}}}}{{{S_{\Delta DEB}}}} = \frac{{FG}}{{BE}} = \frac{1}{6}\) \( \Rightarrow {S_{\Delta DFG}} = \frac{1}{6}{S_{\Delta DEB}}.\)
\(\left\{ \begin{array}{l}{S_{\Delta DEB}} = \frac{1}{2}d\left( {D;\,\,BE} \right).BE\\{S_{\Delta BEC}} = \frac{1}{2}d\left( {C;\,\,BE} \right).BE\end{array} \right.\)\( \Rightarrow \frac{{{S_{\Delta DEB}}}}{{{S_{\Delta BEC}}}} = \frac{{d\left( {D;\,\,BE} \right)}}{{d\left( {C;\,\,BE} \right)}} = \frac{{BD}}{{BC}} = \frac{4}{5}\)\( \Rightarrow {S_{\Delta DEB}} = \frac{4}{5}{S_{\Delta BEC}}.\)
\(\left\{ \begin{array}{l}{S_{\Delta BEC}} = \frac{1}{2}d\left( {B;\,\,EC} \right).EC\\{S_{\Delta ABC}} = \frac{1}{2}d\left( {B;\,\,AC} \right).AC\end{array} \right.\) \( \Rightarrow \frac{{{S_{\Delta BEC}}}}{{{S_{\Delta ABC}}}} = \frac{{EC}}{{AC}} = \frac{3}{4}\)\( \Rightarrow {S_{\Delta BEC}} = \frac{3}{4}{S_{\Delta ABC}}.\)
\( \Rightarrow {S_{\Delta DFG}} = \frac{1}{6}.\frac{4}{5}.\frac{3}{4}.{S_{\Delta ABC}} = \frac{1}{{10}}.900 = 90\,c{m^2}.\)
Chọn B.
Câu hỏi 39 :
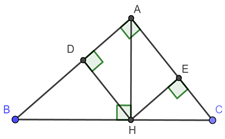
Cho tam giác ABC vuông tại A, đường cao AH. Vẽ \(HD \bot AB\) tại D, \(HE \bot AC\) tại E.
Chứng minh: \(BD = BC{\cos ^3}B\).
Phương pháp giải:
Sử dụng hệ thức lượng trong tam giác vuông.
Sử dụng hệ thức liên hệ giữa cạnh và góc trong tam giác vuông.
Lời giải chi tiết:
Áp dụng hệ thức lượng trong \(\Delta ABH\) vuông tại \(H\) có đường cao \(DH\) ta có: \(BD.BA = B{H^2}\,\,\,\left( 1 \right)\)
Áp dụng hệ thức lượng trong \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH\) ta có: \(BH.BC = B{A^2} \Leftrightarrow BH = \frac{{B{A^2}}}{{BC}}\)\(\left( 2 \right)\)
Từ \(\left( 1 \right)\)và \(\left( 2 \right)\)\( \Rightarrow BD.BA = \frac{{B{A^4}}}{{B{C^2}}} \Rightarrow BD = \frac{{B{A^3}}}{{B{C^2}}}\)
Xét \(\Delta ABC\) vuông tại \(A\) ta có: \(BA = BC\cos B\)
\( \Rightarrow BD = \frac{{B{A^3}}}{{B{C^2}}} = \frac{{B{C^3}{{\cos }^3}B}}{{B{C^2}}}\)\( = BC{\cos ^3}B\,\,\,\,\left( {dpcm} \right).\)
Câu hỏi 40 :
Cho tam giác ABC vuông tại A, đường cao AH. Chứng minh rằng: \(BH = BC{\cos ^2}B\)
Phương pháp giải:
Sử dụng hệ thức lượng trong tam giác vuông.
Sử dụng hệ thức liên hệ giữa cạnh và góc trong tam giác vuông.
Lời giải chi tiết:
Áp dụng hệ thức lượng trong \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH\) ta có:
\(BH.BC = B{A^2} \Leftrightarrow BH = \frac{{B{A^2}}}{{BC}}\)\(\left( 1 \right)\)
Xét \(\Delta ABC\) vuông tại \(A\) ta có:
\(BA = BC\cos B\) \(\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\)\( \Rightarrow BH = \frac{{B{C^2}.{{\cos }^2}B}}{{BC}} = BC.{\cos ^2}B\)
>> Học trực tuyến lớp 9 và Lộ trình UP10 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Lộ trình học tập 3 giai đoạn: Học nền tảng lớp 9, Ôn thi vào lớp 10, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
 |
 |
 |
 |
 |
 |
Các bài khác cùng chuyên mục