40 bài tập trắc nghiệm về tích vô hướng của hai vectơ mức độ vận dụng, vận dụng cao
Làm đề thiCâu hỏi 1 :
Cho tam giác ABC có A(1;2), B(-2;6), C(9;8). Nhận dạng tam giác ABC
- A
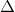 ABC đều
ABC đều - B
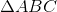 cân
cân - C
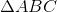 thường
thường - D
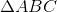 vuông
vuông
Đáp án: D
Lời giải chi tiết:

Câu hỏi 2 :
Cho tam giác ABC có A(-1;1), B(3;1), C(2;4).Tìm toạ độ trực tâm H và trọng tâm G của tam giác.
- A H(2;2), G(
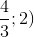
- B H(1;2), G
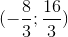
- C H(-1;2); G
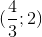
- D H(3;-2); G
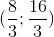
Đáp án: A
Lời giải chi tiết:
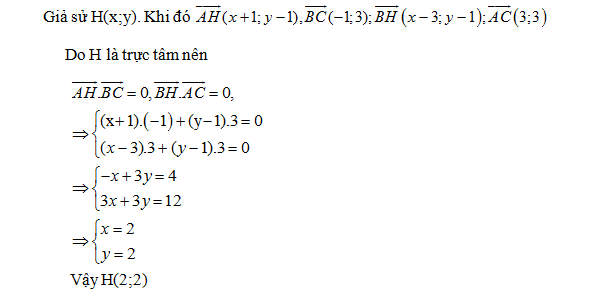
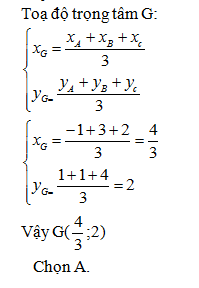
Câu hỏi 3 :
Cho hai điểm A(-3;2), B(4;3). Điểm M nằm trên trục Ox sao cho tam giác MAB vuông tại M. Khi đó M có toạ độ:
- A (2;4) hoặc (5;0)
- B (2;0) hoặc (5;0)
- C (3;0) hoặc (-2;0)
- D (2;0) hoặc (-2;0)
Đáp án: C
Lời giải chi tiết:
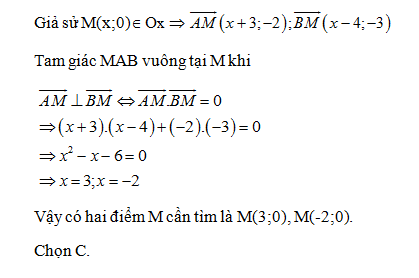
Câu hỏi 4 :
Cho ∆ ABC đều, cạnh AB = 10. Biết rằng 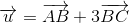 . Khi đó
. Khi đó 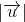 bằng:
bằng:
- A
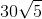
- B 60
- C
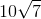
- D 40
Đáp án: C
Lời giải chi tiết:
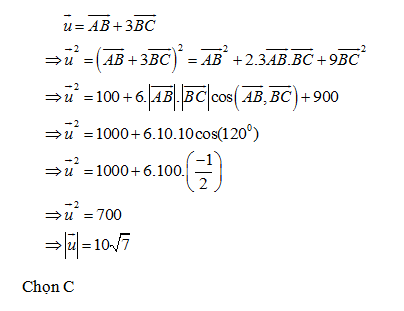
Câu hỏi 5 :
Cho tam giác ABC vuông tại C có AC = 9 và BC = 5. Tính \(\overrightarrow {AB} .\overrightarrow {AC} \).
- A 81
- B 45
- C 96
- D 63
Đáp án: A
Phương pháp giải:
Vận dụng công thức định nghĩa tích vô hướng hai vector \(\overrightarrow {AB} .\overrightarrow {AC} = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|.\cos \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right).\)
Lời giải chi tiết:
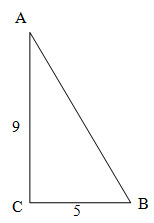
Ta có: \(\overrightarrow {AB} .\overrightarrow {AC} = AB.AC.c{\rm{os}}\left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right)\)
AC = 9. Tính AB. Áp dụng định lý Py-ta-go:
\(AB = \sqrt {A{C^2} + B{C^2}} = \sqrt {{5^2} + {9^2}} = \sqrt {106} \)
\(c{\rm{os}}\left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = c{\rm{os }}\widehat {{\rm{BAC}}}{\rm{ = }}{{AC} \over {AB}} = {9 \over {\sqrt {106} }}\)
Vậy \(\overrightarrow {AB} .\overrightarrow {AC} = AB.AC.c{\rm{os}}\left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = \sqrt {106} .9.{9 \over {\sqrt {106} }} = 81\)
Chọn A.
Câu hỏi 6 :
Trong mặt phẳng tọa độ Oxy cho tam giác ABC với A(0;3); B(2;2) và C(-6;1). Tính số đo góc A.
- A 300
- B 450
- C 1350
- D 1500
Đáp án: C
Phương pháp giải:
Từ công thức \({\rm{cos A = cos(}}\overrightarrow {AB} ;\overrightarrow {AC} ){\rm{ = }}{{\overrightarrow {AB} .\overrightarrow {AC} } \over {\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|}}\) tìm được số đo góc A.
Lời giải chi tiết:
\(\overrightarrow {AB} = \left( {2; - 1} \right);\overrightarrow {AC} = \left( { - 6; - 2} \right)\);
\(\eqalign{ & {\rm{cos A = cos(}}\overrightarrow {AB} ;\overrightarrow {AC} ){\rm{ = }}{{\overrightarrow {AB} .\overrightarrow {AC} } \over {\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|}} \cr & = {{2.\left( { - 6} \right) + \left( { - 1} \right).\left( { - 2} \right)} \over {\sqrt {{2^2} + {{\left( { - 1} \right)}^2}} .\sqrt {{{\left( { - 6} \right)}^2} + {{\left( { - 2} \right)}^2}} }} = {{ - 10} \over {\sqrt 5 .\sqrt {40} }} = {{ - 10} \over {10\sqrt 2 }} = {{ - 1} \over {\sqrt 2 }}. \cr & \Rightarrow \widehat A = {135^0}. \cr} \)
Chọn C.
Câu hỏi 7 :
Trong hệ mặt phẳng tọa độ Oxy cho tam giác ABC có A(1; -1); B(2; 0), C(11; -6). Gọi H(x, y) là trực tâm tam giác ABC. Tính giá trị của x + y?
- A 5
- B 3
- C 2
- D 4
Đáp án: A
Phương pháp giải:
H là trực tâm của tam giác ABC khi và chỉ khi \(\left\{ \matrix{AH \bot BC \hfill \cr BH \bot AC \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{\overrightarrow {AH} .\overrightarrow {BC} = 0 \hfill \cr \overrightarrow {BH} .\overrightarrow {AC} = 0 \hfill \cr} \right.\)
Lời giải chi tiết:
Ta có: \(\overrightarrow {AH} = \left( {x - 1,y + 1} \right);\overrightarrow {BH} \left( {x - 2,y} \right),\overrightarrow {BC} = \left( {9; - 6} \right);\overrightarrow {AC} = \left( {10; - 5} \right).\)
H là trực tâm của tam giác ABC khi và chỉ khi \(\left\{ \matrix{AH \bot BC \hfill \cr BH \bot AC \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{\overrightarrow {AH} .\overrightarrow {BC} = 0 \hfill \cr \overrightarrow {BH} .\overrightarrow {AC} = 0 \hfill \cr} \right.\)
\( \Leftrightarrow \left\{ \matrix{9\left( {x - 1} \right) - 6\left( {y + 1} \right) = 0 \hfill \cr 10\left( {x - 2} \right) - 5y = 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{9x - 6y = 15 \hfill \cr 10x - 5y = 20 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{x = 3 \hfill \cr y = 2 \hfill \cr} \right. \Rightarrow x + y = 5.\)
Chọn A.
Câu hỏi 8 :
Trong mặt phẳng tọa độ Oxy cho hai điểm A(2;4) và B(1;1). Tìm độ điểm C sao cho tam giác ABC vuông cân tại B.
- A C(4;0) và C(2;2)
- B C(4;0) và C(2;-2)
- C C(4;0) và C(-2;-2)
- D C(4;0) và C(-2;2)
Đáp án: D
Phương pháp giải:
- Tọa độ hóa điểm C bằng cách gọi C(a; b).
- Tam giác ABC vuông cân tại B \( \Leftrightarrow \left\{ \matrix{ BA \bot BC \hfill \cr BA = BC \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ \overrightarrow {BA} .\overrightarrow {BC} = 0 \hfill \cr \left| {\overrightarrow {BA} } \right| = \left| {\overrightarrow {BC} } \right| \hfill \cr} \right.\)
- Sử dụng các công thức tích vô hướng của 2 vector, công thức tính độ dài vector \(\overrightarrow u \left( {a;b} \right) \Rightarrow \left| {\overrightarrow u } \right| = \sqrt {{a^2} + {b^2}.} \)
Lời giải chi tiết:
Tam giác ABC vuông cân tại B \( \Rightarrow \left\{ \matrix{ BA \bot BC \hfill \cr BA = BC \hfill \cr} \right. \Rightarrow \left\{ \matrix{ \overrightarrow {BA} .\overrightarrow {BC} = 0 \hfill \cr {\left| {\overrightarrow {BA} } \right|^2} = {\left| {\overrightarrow {BC} } \right|^2} \hfill \cr} \right.\)
Gọi tọa độ C(a; b) ta có: \(\overrightarrow {BA} = \left( {2 - 1;4 - 1} \right) = \left( {1;3} \right)\,;\,\overrightarrow {BC} = \left( {a - 1;b - 1} \right).\)
\( \Rightarrow \left\{ \matrix{ \overrightarrow {BA} .\overrightarrow {BC} = 1.\left( {a - 1} \right) + 3.\left( {b - 1} \right) = 0 \hfill \cr {1^2} + {3^2} = {\left( {a - 1} \right)^2} + {\left( {b - 1} \right)^2} \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ a + 3b = 4 \hfill \cr {(a - 1)^2} + {(b - 1)^2} = 10 \hfill \cr} \right.\)
Thay a = 4 – 3b vào phương trình dưới ta được \(\eqalign{ & {\left( {4 - 3b - 1} \right)^2} + {\left( {b - 1} \right)^2} = 10 \Leftrightarrow {\left( {3 - 3b} \right)^2} + {\left( {b - 1} \right)^2} = 10 \cr & \Leftrightarrow 9{\left( {b - 1} \right)^2} + {\left( {b - 1} \right)^2} = 10 \Leftrightarrow {\left( {b - 1} \right)^2} = 1 \cr} \)
Giải ra ta được hoặc b = 0 hoặc b = 2.
Với b = 2 Þ a = – 2 \( \Rightarrow C\left( { - 2;2} \right).\)
Với b = 0 \( \Rightarrow a = 4 \Rightarrow C\left( {4;0} \right)\).
Chọn D.
Câu hỏi 9 :
Cho ba vector \(\overrightarrow a ,\,\,\overrightarrow b ,\,\,\overrightarrow c \) thỏa mãn \(\left| {\overrightarrow a } \right| = a,\,\,\left| {\overrightarrow b } \right| = b,\,\,\left| {\overrightarrow c } \right| = c\) và \(\overrightarrow a + \overrightarrow b + 3\overrightarrow c = \overrightarrow 0 \). Tính \(A = \overrightarrow a .\overrightarrow b + \overrightarrow b .\overrightarrow c + \overrightarrow c .\overrightarrow a \)
- A \(A = {1 \over 2}\left( {{c^2} - {a^2} - {b^2}} \right)\)
- B \(A = {1 \over 2}\left( {2{c^2} - {a^2} - {b^2}} \right)\)
- C \(A = {1 \over 2}\left( {3{c^2} - {a^2} - {b^2}} \right)\)
- D \(A = {1 \over 2}\left( {3{c^2} + {a^2} - {b^2}} \right)\)
Đáp án: C
Phương pháp giải:
Dựa trên mối liên hệ đã cho biến đổi về dạng chứa \(\overrightarrow a .\overrightarrow b + \overrightarrow b .\overrightarrow c + \overrightarrow c .\overrightarrow a \)
Lời giải chi tiết:
Cách giải:
Ta có \(\overrightarrow a + \overrightarrow b + 3\overrightarrow c = \overrightarrow 0 \Leftrightarrow \overrightarrow a + \overrightarrow b + \overrightarrow c = - 2\overrightarrow c \Leftrightarrow {\left( {\overrightarrow a + \overrightarrow b + \overrightarrow c } \right)^2} = 4{\overrightarrow c ^2} \Leftrightarrow {a^2} + {b^2} + {c^2} + 2A = 4{c^2}\)
Do đó \(A = {1 \over 2}\left( {3{c^2} - {a^2} - {b^2}} \right)\).
Chọn C.
Câu hỏi 10 :
Cho tam giác ABC vuông cân tại A. Tính cos góc giữa hai trung tuyến BE,CF.
- A \(\cos a = {1 \over 5}\)
- B \(\cos a = {2 \over 5}\)
- C \(\cos a = {4 \over 5}\)
- D Kết quả khác
Đáp án: C
Phương pháp giải:
Sử dụng công thức tính góc giữa hai vector: \(\cos a = {{\left| {\overrightarrow {BE} .\overrightarrow {CF} } \right|} \over {\left| {\overrightarrow {BE} } \right|\left| {\overrightarrow {CF} } \right|}}\) , phân tích biểu thức tích vô hướng về dạng đặc biệt.
Lời giải chi tiết:
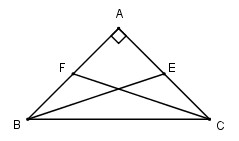
Gọi a là góc tạo bởi hai trung tuyến BE,CF.
Khi đó \(\cos a = {{\left| {\overrightarrow {BE} .\overrightarrow {CF} } \right|} \over {\left| {\overrightarrow {BE} } \right|\left| {\overrightarrow {CF} } \right|}}\)
Sử dụng phân tích
\(\eqalign{ & \overrightarrow {BE} .\overrightarrow {CF} = \left( {\overrightarrow {BA} + \overrightarrow {AE} } \right)\left( {\overrightarrow {CA} + \overrightarrow {AF} } \right) \cr & = \overrightarrow {BA} .\overrightarrow {CA} + \overrightarrow {BA} .\overrightarrow {AF} + \overrightarrow {AE} .\overrightarrow {CA} + \overrightarrow {AE} .\overrightarrow {AF} \cr & = 0 - \overrightarrow {AB} .{{\overrightarrow {AB} } \over 2} - \overrightarrow {AC} {{\overrightarrow {AC} } \over 2} + 0 \cr & = - {{A{B^2}} \over 2} - {{A{C^2}} \over 2} = - {{A{B^2}} \over 2} - {{A{B^2}} \over 2} = - A{B^2}. \cr} \)
\(BE = CF = \sqrt {A{B^2} + A{E^2}} = \sqrt {A{B^2} + {{A{B^2}} \over 4}} = AB\sqrt {{5 \over 4}} \)
Từ đó suy ra \(\cos a = {{A{B^2}} \over {A{B^2}{5 \over 4}}} = {4 \over 5}.\)
Chọn C.
Câu hỏi 11 :
Tìm góc giữa hai đường thẳng \({\Delta _1}:\,x - \sqrt 3 y + 6 = 0,{\Delta _2}:\,x + 10 = 0\).
- A \({30^0}\)
- B \({45^0}\)
- C \({125^0}\)
- D \({60^0}\)
Đáp án: D
Phương pháp giải:
Lấy \(\overrightarrow {{n_1}} \left( {{a_1};{b_1}} \right),\,\,\overrightarrow {{n_2}} \left( {{a_2};{b_2}} \right)\) lần lượt là VTPT của \({\Delta _1},\,{\Delta _2}\). Khi đó, góc giữa hai đường thẳng \({\Delta _1},\,{\Delta _2}\) được tính:
\(\cos \left( {\widehat {{\Delta _1};{\Delta _2}}} \right) = {{\left| {\overrightarrow {{n_1}} .\overrightarrow {{n_2}} } \right|} \over {\left| {\overrightarrow {{n_1}} } \right|.\left| {\overrightarrow {{n_2}} } \right|}}\)
Lời giải chi tiết:
\({\Delta _1}:\,x - \sqrt 3 y + 6 = 0\) có 1 VTPT \(\overrightarrow {{n_1}} \left( {1; - \sqrt 3 } \right)\), \({\Delta _2}:\,x + 10 = 0\) có 1 VTPT \(\overrightarrow {{n_2}} \left( {1;0} \right)\)
Góc giữa hai đường thẳng \({\Delta _1},\,{\Delta _2}: \cos \left( {\widehat {{\Delta _1};{\Delta _2}}} \right) = {{\left| {\overrightarrow {{n_1}} .\overrightarrow {{n_2}} } \right|} \over {\left| {\overrightarrow {{n_1}} } \right|.\left| {\overrightarrow {{n_2}} } \right|}} = {{\left| {1.1 + \left( { - \sqrt 3 } \right).0} \right|} \over {\sqrt {{1^2} + {{\left( { - \sqrt 3 } \right)}^2}} .\sqrt {{1^2} + {0^2}} }} = {1 \over 2} \Rightarrow \widehat {\left( {{\Delta _1};{\Delta _2}} \right)} = {60^0}\)
Chọn: D
Câu hỏi 12 :
Cho tam giác ABC có \(A\left( {5;3} \right);\,\,B\left( {2; - 1} \right);\,\,C\left( { - 1;5} \right)\). Tìm tọa độ trực tâm H của tam giác ABC.
- A \(H\left( { - 3;2} \right)\)
- B \(H\left( { - 3; - 2} \right)\)
- C \(H\left( {3;2} \right)\)
- D \(H\left( {3; - 2} \right)\)
Đáp án: C
Phương pháp giải:
H là trực tâm của tam giác ABC \( \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {HA} .\overrightarrow {BC} = 0\\\overrightarrow {HB} .\overrightarrow {AC} = 0\end{array} \right.\)
Lời giải chi tiết:
Gọi \(H\left( {a;b} \right)\). Ta có:
\(\begin{array}{l}\overrightarrow {HA} = \left( {5 - a;3 - b} \right);\,\,\overrightarrow {BC} = \left( { - 3;6} \right)\\\overrightarrow {HB} = \left( {2 - a; - 1 - b} \right);\,\,\overrightarrow {AC} = \left( { - 6;2} \right)\end{array}\)
H là trực tâm của tam giác ABC \( \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {HA} .\overrightarrow {BC} = 0\\\overrightarrow {HB} .\overrightarrow {AC} = 0\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l} - 3\left( {5 - a} \right) + 6\left( {3 - b} \right) = 0\\ - 6\left( {2 - a} \right) + 2\left( { - 1 - b} \right) = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3a - 6b + 3 = 0\\6a - 2b - 14 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 3\\b = 2\end{array} \right. \Rightarrow H\left( {3;2} \right)\)
Chọn đáp án C.
Câu hỏi 13 :
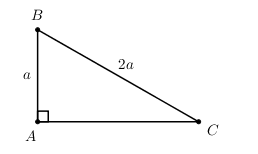
Cho tam giác ABC vuông tại A có \(AB = a;\,\,BC = 2a\). Tính \(\overrightarrow {BC} .\overrightarrow {CA} + \overrightarrow {BA} .\overrightarrow {AC} \) theo a?
- A \(\overrightarrow {BC} .\overrightarrow {CA} + \overrightarrow {BA} .\overrightarrow {AC} = - a\sqrt 3 \)
- B
\(\overrightarrow {BC} .\overrightarrow {CA} + \overrightarrow {BA} .\overrightarrow {AC} = - 3{a^2}\)
- C \(\overrightarrow {BC} .\overrightarrow {CA} + \overrightarrow {BA} .\overrightarrow {AC} = a\sqrt 3 \)
- D \(\overrightarrow {BC} .\overrightarrow {CA} + \overrightarrow {BA} .\overrightarrow {AC} = 3{a^2}\)
Đáp án: D
Phương pháp giải:
Sử dụng công thức \(\overrightarrow u .\overrightarrow v = \left| {\overrightarrow u } \right|.\left| {\overrightarrow v } \right|.\cos \widehat {\left( {\overrightarrow u ;\overrightarrow v } \right)}\).
Lời giải chi tiết:
Ta có \(\sin C = \frac{{AB}}{{BC}} = \frac{a}{{2a}} = \frac{1}{2} \Rightarrow \widehat C = {30^0} \Rightarrow \widehat B = {60^0}\)
Áp dụng định lí Pytago ta có: \(AC = \sqrt {4{a^2} - {a^2}} = a\sqrt 3 \)
\(\begin{array}{l}\,\,\,\,\overrightarrow {BC} .\overrightarrow {CA} + \overrightarrow {BA} .\overrightarrow {AC} \\ = BC.CA.\cos \widehat {\left( {\overrightarrow {BC} ;\overrightarrow {CA} } \right)} + BA.AC.\cos \widehat {\left( {\overrightarrow {BA} ;\overrightarrow {AC} } \right)}\\ = 2a.a\sqrt 3 .\cos {30^0} + a.a\sqrt 3 .\cos {90^0}\\ = 2{a^2}\sqrt 3 .\frac{{\sqrt 3 }}{2} = 3{a^2}\end{array}\)
Chọn đáp án D.
Câu hỏi 14 :
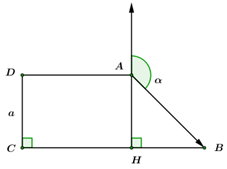
Cho hình thang cân ABCD, biết \(CD = 3AB = 3a\) và \(\widehat {ADC} = {45^0}\). AH vuông góc với CD tại H. Tính cách vô hướng \(\overrightarrow {AH} .\left( {2\overrightarrow {AD} - 3\overrightarrow {CD} } \right);\,\,\overrightarrow {AC} .\overrightarrow {BH} \).
- A \( - 2{a^2};\,\,{a^2}\)
- B \({a^2};\,\, - 2{a^2}\)
- C \({a^2};\,\, - {a^2}\)
- D \(2{a^2};\,\, - {a^2}\)
Đáp án: D
Phương pháp giải:
Sử dụng công thức \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ;\overrightarrow b } \right)\).
Lời giải chi tiết:
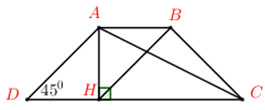
\( + )\,\,\overrightarrow {AH} .\left( {2\overrightarrow {AD} - 3\overrightarrow {CD} } \right) = 2\overrightarrow {AH} .\overrightarrow {AD} - 3\overrightarrow {AH} .\overrightarrow {CD} = 2AH.AD.\cos \widehat {HAD}\).
Ta có: \(\Delta AHD\) có \(\widehat {ADH} = {45^0} \Rightarrow \Delta AHD\) vuông cân tại H.
Ta có: \(HD = \dfrac{{3a - a}}{2} = a = AH \Rightarrow AD = a\sqrt 2 \) và \(\widehat {HAD} = {45^0}\)
\( \Rightarrow \overrightarrow {AH} \left( {2\overrightarrow {AD} - 3\overrightarrow {CD} } \right) = 2.a.a\sqrt 2 .\cos {45^0} = 2{a^2}\sqrt 2 .\dfrac{{\sqrt 2 }}{2} = 2{a^2}\)
\(\begin{array}{l} + )\,\,\overrightarrow {AC} .\overrightarrow {BH} = \left( {\overrightarrow {AH} + \overrightarrow {HC} } \right)\left( {\overrightarrow {AH} - \overrightarrow {AB} } \right) = A{H^2} - \underbrace {\overrightarrow {AB} .\overrightarrow {AH} }_0 + \underbrace {\overrightarrow {AH} .\overrightarrow {HC} }_0 - \overrightarrow {AB} .\overrightarrow {HC} \\ = A{H^2} - \overrightarrow {AB} .\overrightarrow {HC} = A{B^2} - AB.HC.\cos 0 = A{B^2} - AB.HC\\ = {a^2} - a.2a = - {a^2}\end{array}\)
Câu hỏi 15 :
Cho hình chữ nhật ABCD. AB = 4, AD = 3. Khi đó \(\overrightarrow {AB} .\overrightarrow {AD} \) bằng:
- A 0
- B 12
- C 5
- D Đáp án khác
Đáp án: A
Phương pháp giải:
Sử dụng kiến thức: \(\overrightarrow a \bot \overrightarrow b \Rightarrow \overrightarrow a .\overrightarrow b = 0\)
Lời giải chi tiết:
ABCD là hình chữ nhật \( \Rightarrow AB \bot AD \Rightarrow \overrightarrow {AB} \bot \overrightarrow {AD} \Rightarrow \overrightarrow {AB} .\overrightarrow {AD} = \ 0 \)
Chọn A.
Câu hỏi 16 :
Trong mặt phẳng tọa độ \(Oxy,\) cho tam giác \(ABC\) có \(A\left( { - 3;0} \right),{\rm{ }}B\left( {3;0} \right)\) và \(C\left( {2;6} \right).\) Gọi \(H\left( {a;b} \right)\) là tọa độ trực tâm của tam giác đã cho. Tính \(a + 6b.\)
- A \(a + 6b = 5.\)
- B \(a + 6b = 6.\)
- C \(a + 6b = 7.\)
- D \(a + 6b = 8.\)
Đáp án: C
Phương pháp giải:
H là trực tâm của tam giác ABC \( \Rightarrow \left\{ \begin{array}{l}\overrightarrow {AH} .\overrightarrow {BC} = 0\\\overrightarrow {BH} .\overrightarrow {AC} = 0\end{array} \right.\).
Lời giải chi tiết:
Gọi \(H\left( {a;b} \right)\). Ta có \(\overrightarrow {BC} = \left( { - 1;6} \right);\,\,\overrightarrow {AC} = \left( {5;6} \right);\,\,\,\overrightarrow {AH} = \left( {a + 3;b} \right);\,\,\overrightarrow {BH} = \left( {a - 3;b} \right)\).
Vì H là trực tâm của tam giác ABC \( \Rightarrow \left\{ \begin{array}{l}\overrightarrow {AH} .\overrightarrow {BC} = 0\\\overrightarrow {BH} .\overrightarrow {AC} = 0\end{array} \right.\).
\( \Leftrightarrow \left\{ \begin{array}{l} - a - 3 + 6b = 0\\5a - 15 + 6b = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b = \dfrac{5}{6}\end{array} \right. \Rightarrow a + 6b = 2 + 5 = 7\).
Chọn C.
Câu hỏi 17 :
Cho tam giác ABC đều cạnh bằng a, nội tiếp đường tròn tâm O. Khi đó \(\overrightarrow {AO} .\overrightarrow {OB} \) bằng:
- A \(\dfrac{{{a^2}}}{6}\)
- B \( - \dfrac{{{a^2}}}{6}\)
- C \(\dfrac{{{a^2}}}{{2\sqrt 3 }}\)
- D \( - \dfrac{{{a^2}}}{{2\sqrt 3 }}\)
Đáp án: A
Phương pháp giải:
Sử dụng công thức \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ;\overrightarrow b } \right)\).
Lời giải chi tiết:
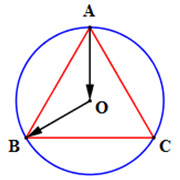
Vì tam giác ABC đều cạnh a nên \(OA = OB = \dfrac{2}{3}\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{3}\).
Ta có \(\left( {\overrightarrow {AO} ;\overrightarrow {BO} } \right) = {60^0}\)
Vậy \(\overrightarrow {AO} .\overrightarrow {OB} = OA.OB.\cos \left( {\overrightarrow {AO} ;\overrightarrow {BO} } \right) = {\left( {\dfrac{{a\sqrt 3 }}{3}} \right)^2}.\cos 60 = \dfrac{{{a^2}}}{3}.\dfrac{1}{2} = \dfrac{{{a^2}}}{6}\).
Chọn A.
Câu hỏi 18 :
Cho hình vuông ABCD cạnh a. Tính \(\left( {\overrightarrow {AB} + \overrightarrow {AD} } \right).\left( {\overrightarrow {BC} + \overrightarrow {BD} } \right)\).
- A \( - 2{a^2}\)
- B \({a^2}\)
- C 2\({a^2}\)
- D \( - \frac{{{a^2}}}{{\sqrt 2 }}\)
Đáp án: B
Phương pháp giải:
+) Áp dụng quy tắc hình bình hành : \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} .\)
+) Sử dụng công thức \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ,\overrightarrow b } \right)\)
\( + )\;\overrightarrow a = \left( {{a_1};{a_2}} \right) \bot \,\overrightarrow b = \left( {{b_1};{b_2}} \right) \Rightarrow \overrightarrow a .\overrightarrow b = {a_1}.{b_1} + {a_2}.{b_2} = 0\)
Lời giải chi tiết:
Vì \(ABCD\) là hình vuông \( \Rightarrow \left( {\overrightarrow {AC} ,\;\overrightarrow {BC} } \right) = {45^0},\;\left( {\overrightarrow {AC} ,\;\overrightarrow {BD} } \right) = {90^0}.\)
\(\begin{array}{l}\;\;\left( {\overrightarrow {AB} + \overrightarrow {AD} } \right).\left( {\overrightarrow {BC} + \overrightarrow {BD} } \right) = \overrightarrow {AC} .\left( {\overrightarrow {BC} + \overrightarrow {BD} } \right) = \overrightarrow {AC} .\overrightarrow {BC} + \overrightarrow {AC} .\overrightarrow {BD} \\ = \overrightarrow {AC} .\overrightarrow {BC} = a.a\sqrt 2 .\cos {45^o} = {a^2}.\end{array}\)
Chọn B.
Câu hỏi 19 :
Cho hình vuông ABCD cạnh a. Tính \(\left( {\overrightarrow {AB} + \overrightarrow {AD} } \right).\left( {\overrightarrow {BC} + \overrightarrow {BD} } \right)\).
- A \(\frac{3}{2}\)
- B \(2\)
- C \(\frac{5}{2}\)
- D \(\frac{1}{2}\)
Đáp án: C
Phương pháp giải:
Giải hệ phương trình bằng phương pháp đặt ẩn phụ.
Lời giải chi tiết:
\(\left\{ \begin{array}{l}x + y + xy = \frac{7}{2}\\{x^2}y + x{y^2} = \frac{5}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}xy = \frac{7}{2} - \left( {x + y} \right)\\xy.\left( {x + y} \right) = \frac{5}{2}\end{array} \right.\)
Đặt \(\left\{ \begin{array}{l}x + y = a\\xy = b\end{array} \right.\;\;\left( {{a^2} \ge 4b} \right)\)
\(\begin{array}{l} \Rightarrow Hpt \Leftrightarrow \left\{ \begin{array}{l}b = \frac{7}{2} - a\\ab = \frac{5}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = \frac{7}{2} - a\\a\left( {\frac{7}{2} - a} \right) = \frac{5}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = \frac{7}{2} - a\\{a^2} - \frac{7}{2}a + \frac{5}{2} = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}b = \frac{7}{2} - a\\\left[ \begin{array}{l}a = \frac{5}{2}\\a = 1\end{array} \right.\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}a = \frac{5}{2}\\b = 1\end{array} \right.\;\;\left( {tm} \right)\\\left[ \begin{array}{l}a = 1\\b = \frac{5}{2}\end{array} \right.\;\;\left( {ktm} \right)\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x + y = \frac{5}{2}\\xy = 1\end{array} \right..\end{array}\)
Với \(\left( {{x_0};\;{y_0}} \right)\) là một nghiệm của hệ phương trình \( \Rightarrow {x_0} + {y_0} = \frac{5}{2}.\)
Chọn C.
Câu hỏi 20 :
Cho tam giác ABC vuông tại A; \(AB = a,AC = a\). Tính \(\overrightarrow {BA} .\overrightarrow {BC} \)
- A \( - {a^2}\)
- B \({a^2}\)
- C \( - \frac{{{a^2}}}{2}\)
- D \(0\)
Đáp án: B
Phương pháp giải:
Sử dụng tính chất tam giác vuông cân và công thức \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ,\overrightarrow b } \right)\)
Lời giải chi tiết:
Tam giác ABC vuông tại A; \(AB = AC = a \Rightarrow \Delta ABC\) vuông cân tại \(A,\;\;\left( {\overrightarrow {BA} ,\;\overrightarrow {BC} } \right) = \angle ABC = {45^0}.\)
Sử dụng định lý Pytago ta được: \(BC = \sqrt {A{B^2} + A{C^2}} = a\sqrt 2 \)
\(\overrightarrow {BA} .\overrightarrow {BC} = BA.BC.\cos \left( {\overrightarrow {BA} ,\overrightarrow {BC} } \right) = a.a\sqrt 2 .\cos {45^o} = {a^2}\)
Chọn B.
Câu hỏi 21 :
Trong hệ tọa độ Oxy, cho \(A\left( {2;3} \right),B\left( { - 1; - 4} \right),C\left( {2; - 4} \right)\). Chọn mệnh đề đúng trong các mệnh đề sau:
- A Tam giác ABC vuông tại A
- B Tam giác ABC vuông tại C
- C Tam giác ABC đều
- D Tam giác ABC cân tại A
Đáp án: B
Phương pháp giải:
\(\overrightarrow a = \left( {{a_1};{a_2}} \right) \bot \,\overrightarrow b = \left( {{b_1};{b_2}} \right) \Rightarrow \overrightarrow a .\overrightarrow b = {a_1}.{b_1} + {a_2}.{b_2} = 0\)
Lời giải chi tiết:
Ta có :
\(\overrightarrow {AC} = \left( {0; - 7} \right)\,\,;\,\,\overrightarrow {BC} = \left( {3;0} \right) \Rightarrow \overrightarrow {AC} .\,\overrightarrow {BC} = 0 \Rightarrow \overrightarrow {AC} \bot \,\overrightarrow {BC} \)
\( \Rightarrow \) Tam giác ABC vuông tại C
Chọn B.
Câu hỏi 22 :
Cho hình vuông ABCD. Khẳng định nào sau đây là sai?
- A \(\left( {\overrightarrow {A{\rm{D}}} ,\overrightarrow {AB} } \right) = {90^0}\)
- B \(\left( {\overrightarrow {AB} ,\overrightarrow {CA} } \right) = {45^0}\)
- C \(\left( {\overrightarrow {AD} ,\overrightarrow {BC} } \right) = {0^0}\)
- D \(\left( {\overrightarrow {AB} ,\overrightarrow {C{\rm{D}}} } \right) = {180^0}\)
Đáp án: B
Phương pháp giải:
Sử dụng tính chất hình vuông và tính góc giữa hai vectơ bằng cách đưa về chung gốc.
Lời giải chi tiết:
ABCD là hình vuông \( \Rightarrow \left( {\overrightarrow {AB} ,\overrightarrow {CA} } \right) = {135^o}\)
Chọn B.
Câu hỏi 23 :
Cho véc tơ\(\overrightarrow a = \left( {1; - 2} \right)\). Với giá trị nào của y thì véc tơ \(\overrightarrow b = \left( {3;y} \right)\) tạo với véc tơ \(\overrightarrow a \) một góc \({45^o}\):
- A \(y = - 9\)
- B \(\left[ \begin{array}{l}y = 1\\y = - 9\end{array} \right.\)
- C \(\left[ \begin{array}{l}y = - 1\\y = 9\end{array} \right.\)
- D \(y = - 1\)
Đáp án: D
Phương pháp giải:
Dùng công thức góc giữa hai véc tơ: \(\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}}\)
\(\overrightarrow a = \left( {{a_1};{a_2}} \right);\,\,\overrightarrow b = \left( {{b_1};{b_2}} \right) \Rightarrow \overrightarrow a .\overrightarrow b = {a_1}.{b_1} + {a_2}.{b_2}\,\,;\,\,\left| {\overrightarrow a } \right| = \sqrt {{a_1}^2 + {a_2}^2} \)
Lời giải chi tiết:
Véc tơ \(\overrightarrow b = \left( {3;y} \right)\) tạo với véc tơ \(\overrightarrow a = \left( {1; - 2} \right)\) một góc \({45^o}\)
\(\begin{array}{l} \Rightarrow \cos {45^o} = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}} \Leftrightarrow \frac{{\sqrt 2 }}{2} = \frac{{3 - 2y}}{{\sqrt 5 .\sqrt {9 + {y^2}} }} \Leftrightarrow \frac{{\sqrt {10} }}{2}.\sqrt {9 + {y^2}} = 3 - 2y \Leftrightarrow \left\{ \begin{array}{l}3 - 2y \ge 0\\\frac{5}{2}\left( {9 + {y^2}} \right) = {\left( {3 - 2y} \right)^2}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}y \le \frac{3}{2}\\45 + 5{y^2} = 18 - 24y + 8{y^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y \le \frac{3}{2}\\3{y^2} - 24y - 27 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y \le \frac{3}{2}\\\left[ \begin{array}{l}y = - 1\\y = 9\end{array} \right.\end{array} \right. \Leftrightarrow y = - 1.\end{array}\)
Chọn D.
Câu hỏi 24 :
Cho hai điểm \(A,B\) cố định và \(AB = 8.\) Tập hợp các điểm \(M\) thoả mãn \(\overrightarrow {MA} .\overrightarrow {MB} = - 16\) là:
- A một điểm
- B đường thẳng
- C đoạn thẳng
- D đường tròn
Đáp án: A
Phương pháp giải:
Ta lấy trung điểm I của đoạn thẳng \(AB\) , rồi sau đó biến đổi \(\overrightarrow {MA} .\overrightarrow {MB} \) thông qua hai vecto \(\overrightarrow {MI} ,\overrightarrow {AB} \) cố định
Lời giải chi tiết:
Gọi \(I\) là trung điểm của đoạn thẳng \(AB\), suy ra \(\overrightarrow {IA} = - \overrightarrow {IB} .\)
Ta có: \(\overrightarrow {MA} .\overrightarrow {MB} = \left( {\overrightarrow {MI} + \overrightarrow {IA} } \right)\left( {\overrightarrow {MB} + \overrightarrow {IB} } \right) = \left( {\overrightarrow {MI} + \overrightarrow {IA} } \right)\left( {\overrightarrow {MI} - \overrightarrow {IA} } \right) = {\overrightarrow {MI} ^2} - {\overrightarrow {IA} ^2} = M{I^2} - I{A^2} = M{I^2} - \frac{{A{B^2}}}{4}\)
Theo giả thiết, ta có: \(M{I^2} - \frac{{A{B^2}}}{4} = - 16 \Leftrightarrow M{I^2} = \frac{{A{B^2}}}{4} - 16 = \frac{{{8^2}}}{4} - 16 = 0\,\, \to M \equiv I\)
Chọn A.
Câu hỏi 25 :
Cho hai điểm \(A,\) \(B\)cố định có khoảng cách bằng \(a.\) Tập hợp các điểm \(N\) thoả mãn \(\overrightarrow {AN} .\overrightarrow {AB} = 2{a^2}\) là:
- A một điểm
- B đường thẳng
- C đoạn thẳng
- D đường tròn
Đáp án: B
Phương pháp giải:
Ta lấy điểm đối xứng của \(A\) qua \(B\) , rồi sau đó biến đổi vecto có \(N\) thông qua một vecto khác cố định
Lời giải chi tiết:
Lấy điểm \(C\) là điểm đối xứng của \(A\) qua \(B\).
Khi đó \(\overrightarrow {AC} = 2.\overrightarrow {AB} \Rightarrow \overrightarrow {AB} .\overrightarrow {AC} = 2{a^2}.\)
Kết hợp với giả thiết đã cho, ta có: \(\overrightarrow {AN} .\overrightarrow {AB} = \overrightarrow {AB} .\overrightarrow {AC} \Leftrightarrow \overrightarrow {AB} \left( {\overrightarrow {AN} - \overrightarrow {AC} } \right) = 0 \Leftrightarrow \overrightarrow {AB} .\overrightarrow {CN} = 0 \Rightarrow CN \bot AB.\)
Vậy tập hợp các điểm \(N\) là đường thẳng đi qua \(C\) và vuông góc với \(AB.\)
Chọn B.
Câu hỏi 26 :
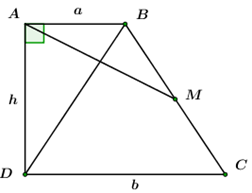
Cho hình thang vuông \(ABCD\), đường cao \(AD = h,\) đáy \(AB = a,\) đáy \(CD = b.\) Gọi \(M\) là trung điểm của \(BC.\) Hệ thức giữa \(a,b,h\) để \(AM \bot BD\) là:
- A \({a^2} - {h^2} - ab = 0\)
- B \({h^2} - {a^2} - ab = 0\)
- C \({h^2} - {b^2} - ab = 0\)
- D \({b^2} - {h^2} - ab = 0\)
Đáp án: B
Phương pháp giải:
+) Ta sử dụng tính chất của hai vecto vuông góc và biến đổi các vecto thông qua 3 vecto \(\overrightarrow {AB} ,\overrightarrow {AD} ,\overrightarrow {DC} \)
+) \(\overrightarrow a \bot \overrightarrow b \Leftrightarrow \overrightarrow a .\overrightarrow b = 0.\)
Lời giải chi tiết:
Ta có:
\(\begin{array}{l}\,\,\,\,\,AM \bot BD \Leftrightarrow 2.\overrightarrow {AM} .\overrightarrow {BD} = 0\\ \Leftrightarrow \left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\overrightarrow {BD} = 0\\ \Leftrightarrow \left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {DC} } \right)\left( {\overrightarrow {AD} - \overrightarrow {AB} } \right) = 0\\ \Leftrightarrow - A{B^2} + A{D^2} - \overrightarrow {DC} .\overrightarrow {AB} = 0\\ \Leftrightarrow {h^2} - {a^2} - ab = 0\end{array}\)
Chọn B
Câu hỏi 27 :
Trong mặt phẳng toạ độ \(Oxy,\) cho hai điểm \(A\left( { - 1;1} \right),B\left( {3;2} \right).\) Tìm \(M\) thuộc trục tung sao cho \(M{A^2} + M{B^2}\) nhỏ nhất.
- A \(M\left( {0;\frac{1}{2}} \right)\)
- B \(M\left( {0; - \frac{1}{2}} \right)\)
- C \(M\left( {0;1} \right)\)
- D \(M\left( {0; - 1} \right)\)
Đáp án: A
Phương pháp giải:
Cho \(\overrightarrow a = \left( {{a_1};{a_2}} \right) \Rightarrow \left| {\overrightarrow a } \right| = \sqrt {{a_1}^2 + {a_2}^2} ;\,\,\,{\overrightarrow a ^2} = {\left| {\overrightarrow a } \right|^2}.\)
Lời giải chi tiết:
Ta có: \(M \in Oy \Rightarrow M\left( {0;\,\,m} \right)\) và \(\left\{ {\begin{array}{*{20}{c}}{\overrightarrow {MA} = \left( {1; - 1 - m} \right)}\\{\overrightarrow {MB} = \left( {3;\,\,2 - m} \right)}\end{array}} \right..\)
Khi đó: \(M{A^2} + M{B^2} = {\left| {\overrightarrow {MA} } \right|^2} + {\left| {\overrightarrow {MB} } \right|^2} = {1^2} + {\left( { - 1 - m} \right)^2} + {3^2} + {\left( {2 - m} \right)^2} = 2{m^2} - 2m + 15 = 2{\left( {m - \frac{1}{2}} \right)^2} + \frac{{29}}{2} \ge \frac{{29}}{2}\forall m \in \mathbb{R}\)
\( \Rightarrow Min\left( {M{A^2} + M{B^2}} \right) = \frac{{29}}{2}.\)
Dấu “=” xảy ra \( \Leftrightarrow m = \frac{1}{2} \Rightarrow M\left( {0;\,\,\frac{1}{2}} \right).\)
Chọn A
Câu hỏi 28 :
Cho tam giác \(ABC\) vuông cân tại \(A,\,\,\,AB = AC = 2.\) Gọi \(M,\,\,N\) lần lượt là trung điểm của \(AC,\,\,AB.\) Tích vô hướng \(\overrightarrow {BM} .\overrightarrow {CN} \) bằng:
- A \( - 4\)
- B \( - 2\)
- C \( - 8\)
- D \(4\)
Đáp án: A
Phương pháp giải:
Phân tích vectơ sau đó áp dụng công thức tích vô hướng của hai vectơ.
Lời giải chi tiết:
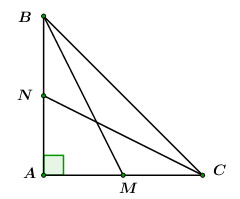
Áp dụng định lý Pitago ta có: \(BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {{2^2} + {2^2}} = 2\sqrt 2 .\)
\(\begin{array}{l}\overrightarrow {BM} .\overrightarrow {CN} = \left( {\overrightarrow {BC} + \overrightarrow {CM} } \right)\left( {\overrightarrow {CB} + \overrightarrow {BN} } \right) = \overrightarrow {BC} .\overrightarrow {CB} + \overrightarrow {BC} .\overrightarrow {BN} + \overrightarrow {CM} .\overrightarrow {CB} + \overrightarrow {CM} .\overrightarrow {BN} \\ = BC.CB.\cos \angle \left( {\overrightarrow {BC} ,\,\,\overrightarrow {CB} } \right) + BC.BN.\cos \angle ABC + CM.CB.\cos \angle ACB + CM.BN.\cos \angle BAC\\ = 2\sqrt 2 .2\sqrt 2 .\cos {180^0} + 2\sqrt 2 .1.\cos {45^0} + 1.2\sqrt 2 \cos {45^0} + 1.1.\cos {90^0}\\ = - {\left( {2\sqrt 2 } \right)^2} + 2\sqrt 2 .1.\frac{{\sqrt 2 }}{2} + 2\sqrt 2 .1.\frac{{\sqrt 2 }}{2} + 0 = - 4.\end{array}\)
Chọn A.
Câu hỏi 29 :
Trong mặt phẳng tọa độ \(Oxy\), cho \(A\left( { - 2;3} \right)\), \(B\left( {8; - 3} \right).\) Điều kiện của \(b\) để điểm \(M\left( {0;b} \right)\) thỏa mãn \(\angle AMB > 90^\circ \) là:
- A \(b \in \left( { - 5;5} \right).\)
- B \(b \in \left( { - \infty ;5} \right).\)
- C \(b < 5.\)
- D \(b \in \left( { - \infty ; - 5} \right) \cup \left( {5; + \infty } \right).\)
Đáp án: A
Phương pháp giải:
Ta có: \(\angle AMB > {90^0} \Rightarrow - 1 \le \cos \angle AMB < 0.\)
Lời giải chi tiết:
Ta có: \(\overrightarrow {AM} = \left( {2;\,\,b - 3} \right),\,\,\,\overrightarrow {BM} = \left( { - 8;\,\,b + 3} \right).\)
\(\begin{array}{l} \Rightarrow \cos \angle AMB = \frac{{\overrightarrow {AM} .\overrightarrow {BM} }}{{\left| {\overrightarrow {AM} } \right|.\left| {\overrightarrow {BM} } \right|}} = \frac{{2.\left( { - 8} \right) + \left( {b - 3} \right)\left( {b + 3} \right)}}{{\sqrt {{2^2} + {{\left( {b - 3} \right)}^2}} \sqrt {{8^2} + {{\left( {b + 3} \right)}^2}} }}\\ = \frac{{ - 16 + {b^2} - 9}}{{\sqrt {4 + {b^2} - 6b + 9} .\sqrt {64 + {b^2} + 6b + 9} }} = \frac{{{b^2} - 25}}{{\sqrt {{b^2} - 6b + 13} .\sqrt {{b^2} + 6b + 73} }}.\end{array}\)
Để \(\angle AMB > 90^\circ \) thì \(\cos \angle AMB < 0 \Leftrightarrow {b^2} - 25 < 0 \Leftrightarrow - 5 < b < 5 \Leftrightarrow b \in \left( { - 5;5} \right).\)
Chọn A.
Câu hỏi 30 :
Trong mặt phẳng \(Oxy,\) cho \(A\left( { - 2;2} \right),\,B\left( {8;2} \right).\) Tìm điểm \(C\) thuộc \(Oy\) sao cho tam giác \(ABC\) vuông tại \(C\)
- A \(C\left( {0; - 6} \right)\) hoặc \(C\left( {0; - 2} \right).\)
- B \(C\left( {0;6} \right)\) hoặc \(C\left( {0; - 2} \right).\)
- C \(C\left( {0;6} \right)\) hoặc \(C\left( {0;2} \right).\)
- D \(C\left( {0; - 6} \right)\) hoặc \(C\left( {0;2} \right).\)
Đáp án: B
Phương pháp giải:
Tam giác \(ABC\) vuông tại \(C\) nên \(AC \bot BC \Leftrightarrow \overrightarrow {AC} .\overrightarrow {BC} = 0\), từ đó ta tìm được tọa độ điểm \(C.\)
Lời giải chi tiết:
Điểm \(C \in Oy \Rightarrow C\left( {0;y} \right)\)
Ta có: \(\overrightarrow {AC} = \left( {2;y - 2} \right),\overrightarrow {BC} = \left( { - 8;y - 2} \right)\)
Vì tam giác \(ABC\) vuông tại \(C\) nên \(AC \bot BC \Leftrightarrow \overrightarrow {AC} .\overrightarrow {BC} = 0\)
\(\begin{array}{l} \Leftrightarrow 2.\left( { - 8} \right) + {\left( {y - 2} \right)^2} = 0\\ \Leftrightarrow {\left( {y - 2} \right)^2} = 16\\ \Leftrightarrow \left[ \begin{array}{l}y - 2 = 4\\y - 2 = - 4\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}y = 6\\y = - 2\end{array} \right.\end{array}\)
Vậy \(C\left( {0;6} \right)\) hoặc \(C\left( {0; - 2} \right).\)
Chọn B.
Câu hỏi 31 :
Cho tam giác \(ABC\) vuông cân tại \(B.\) Gọi \(M\) là trung điểm của \(AB\) và \(I\) là điểm di động trên đường thẳng \(MC.\) Khi \(\left| {2\overrightarrow {IM} + \overrightarrow {AC} } \right|\) đạt giá trị nhỏ nhất, hãy tính tỉ số \(\frac{{AC}}{{AI}}?\)
- A \(\frac{{AC}}{{AI}} = 1\)
- B \(\frac{{AC}}{{AI}} = \frac{3}{2}\)
- C \(\frac{{AC}}{{AI}} = 2\)
- D \(\frac{{AC}}{{AI}} = \sqrt 2 \)
Đáp án: D
Phương pháp giải:
Xác định \(\left| {2\overrightarrow {IM} + \overrightarrow {AC} } \right|\) đạt giá trị nhỏ nhất khi nào, sau đó vận dụng các giả thiết để tìm được tỉ số \(\frac{{AC}}{{AI}}.\)
Lời giải chi tiết:
Gọi \(N\) là trung điểm của \(BC.\)
Có \(\left| {2\overrightarrow {IM} + \overrightarrow {AC} } \right| = \left| {\overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} - \overrightarrow {IA} } \right| = \left| {\overrightarrow {IB} + \overrightarrow {IC} } \right| = 2IN\)
Do đó, \(\left| {2\overrightarrow {IM} + \overrightarrow {AC} } \right|\) đạt giá trị nhỏ nhất \( \Leftrightarrow I\) là hình chiếu vuông góc của \(N\) trên \(MC.\)
Dựng hình vuông \(ABCD.\)
Gọi \(P\) là trung điểm của \(CD\) và \(H\) là giao điểm của \(AP\) và \(DN.\)
Ta chứng minh được \(DN \bot CM \Rightarrow I \in DN.\)
Lại có tứ giác \(AMCP\) là hình bình hành, suy ra \(AP//CM.\)
Do đó\(AP \bot DI\) và \(H\) là trung điểm của \(DI \Rightarrow \Delta AID\) cân tại \(A.\)
Vậy \(\frac{{AC}}{{AI}} = \frac{{AC}}{{AD}} = \sqrt 2 .\)
Chọn D
Câu hỏi 32 :
Cho hình thang vuông \({\rm{ABCD}}\) (vuông tại \(C\) và \(D\)) có \({\rm{CD}} = a\). Khi đó tích vô hướng \(\overrightarrow {AB} .\overrightarrow {CD} \) bằng:
- A \( - {a^2}\)
- B \({a^2}\)
- C \(0\)
- D \( - 2{a^2}\)
Đáp án: A
Phương pháp giải:
Sử dụng công thức tính tích vô hướng: \(\overrightarrow {AB} .\overrightarrow {CD} = AB.CD.\cos \left( {\overrightarrow {AB} ,\,\,\overrightarrow {CD} } \right).\)
Lời giải chi tiết:
Gọi \(H\) là hình chiếu của \(A\) trên \(BC.\)
Gọi \(\angle \left( {\overrightarrow {AB} ,\,\,\overrightarrow {CD} } \right) = \alpha .\) Ta có hình vẽ.
Ta có: \(AH = CD = a.\)
Xét \(\Delta ABH\) ta có: \(AB = \frac{{AH}}{{\cos \angle HAB}} = \frac{{AH}}{{\cos \left( {{{180}^0} - \alpha } \right)}} = \frac{{CD}}{{ - \cos \alpha }}.\)
Áp dụng công thức tích vô hướng ta có:
\(\overrightarrow {AB} .\overrightarrow {CD} = AB.CD.\cos \left( {\overrightarrow {AB} ,\,\,\overrightarrow {CD} } \right) = \frac{{CD}}{{ - \cos \alpha }}.CD.\cos \alpha = - C{D^2} = - {a^2}.\)
Chọn A.
Câu hỏi 33 :
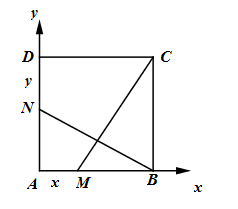
Cho hình vuông ABCD có cạnh bằng 1. Hai điểm M, N thay đổi lần lượt trên AB, D sao cho \(AM = x\,\,\left( {0 \le x \le 1} \right)\) và \(DN = y\,\,\left( {0 \le y \le 1} \right)\). Tìm mối liên hệ giữa x và y sao cho \(CM \bot BN\).
- A \(x - y = 0\)
- B \(x - y\sqrt 2 = 0\)
- C \(x + y = 1\)
- D \(x - y\sqrt 3 = 0\)
Đáp án: A
Phương pháp giải:
+) Gắn hệ trục tọa độ, xác định tọa độ các điểm A, B, C, D, M, N.
+) \(CM \bot BN \Leftrightarrow \overrightarrow {CM} .\overrightarrow {BN} = 0\)
Lời giải chi tiết:
Gắn hệ trục tọa độ như hình vẽ ta có
\(A\left( {0;0} \right);\,\,B\left( {1;0} \right);\,\,C\left( {1;1} \right);\,\,D\left( {0;1} \right);\,\,M\left( {x;0} \right);\,\,N\left( {0;1 - y} \right)\)
\(\begin{array}{l} \Rightarrow \overrightarrow {CM} = \left( {x - 1; - 1} \right);\,\,\overrightarrow {BN} = \left( { - 1;1 - y} \right)\\CM \bot BN \Leftrightarrow \overrightarrow {CM} .\overrightarrow {BN} = 0\\ \Leftrightarrow - x + 1 - 1 + y = 0 \Leftrightarrow x - y = 0\end{array}\)
Chọn đáp án A.
Câu hỏi 34 :
Tam giác ABC có \(A( - 3; - 2),\;B(5;2)\) và trực tâm \(H(5;0)\). Tìm tọa độ đỉnh C.
- A \(C(6; - 2)\).
- B \(C(4; - 2)\).
- C \(C(5; - 2)\).
- D \(C(4; - 1)\).
Đáp án: A
Phương pháp giải:
Gọi tọa độ điểm C theo hai chữ, từ dữ kiện đề bài lập hệ phương trình giải để tìm C
\(\overrightarrow a = \left( {{a_1};{a_2}} \right) \bot \,\overrightarrow b = \left( {{b_1};{b_2}} \right) \Rightarrow \overrightarrow a .\overrightarrow b = {a_1}.{b_1} + {a_2}.{b_2} = 0\)
Lời giải chi tiết:
Gọi \(C\left( {{x_0};{y_0}} \right)\) là điểm cần tìm.
Ta có : \(\overrightarrow {AH} = \left( {8;2} \right)\,\,;\,\,\overrightarrow {BC} = \left( {{x_0} - 5;{y_0} - 2} \right)\)
\(\overrightarrow {AB} = \left( {8;4} \right)\,\,;\,\,\overrightarrow {CH} = \left( {5 - {x_0}; - {y_0}} \right)\)
H là trực tâm tam giác ABC \( \Rightarrow \left\{ \begin{array}{l}\overrightarrow {AH} \bot \overrightarrow {BC} \\\overrightarrow {CH} \bot \overrightarrow {AB} \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}8\left( {{x_0} - 5} \right) + 2\left( {{y_0} - 2} \right) = 0\\8\left( {5 - {x_0}} \right) + 4\left( { - {y_0}} \right) = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}8{x_0} + 2{y_0} = 44\\ - 8{x_0} - 4{y_0} = - 40\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_0} = 6\\{y_0} = - 2\end{array} \right.\)
Chọn A.
Câu hỏi 35 :
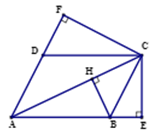
Cho hình bình hành \(ABCD\) có đường chéo lớn là \(AC.\) Gọi \(E,F\) lần lượt là hình chiếu vuông góc của \(C\) trên \(AB,AD.\) Biểu thức nào sau đây là đúng?
- A \(AB.AH + AD.AF = A{C^2}\)
- B \(AB.AE + AD.AH = A{C^2}\)
- C \(AB.AE + AD.AF = AC.AH\)
- D \(AB.AE + AD.AF = A{C^2}\)
Đáp án: D
Phương pháp giải:
+) Từ hai hình chiếu của \(C\) lên \(AB,AD\), ta biến đổi các các đẳng thức theo đề bài để đưa ra đáp án đúng.
Lời giải chi tiết:
Vì \(E,F\) lần lượt là hình chiếu của \(C\) lên \(AB,AD\) nên ta có:
\(\begin{array}{l}\overrightarrow {AB} .\overrightarrow {AE} = \overrightarrow {AC} .\overrightarrow {AB} \\\overrightarrow {AD} .\overrightarrow {AF} = \overrightarrow {AC} .\overrightarrow {AD} \end{array}\)
Suy ra \(\overrightarrow {AB} .\overrightarrow {AE} + \overrightarrow {AD} .\overrightarrow {AF} = \overrightarrow {AC} .\overrightarrow {AB + } \overrightarrow {AC} .\overrightarrow {AD} = {\overrightarrow {AC} ^2}\left( * \right)\)
Do \(AC\) là đường chéo lớn nên \(\angle ABC \ge {90^o}\) và \(B\) nằm giữa hai điểm \(A\) và \(E.\) Suy ra \(\overrightarrow {AB} .\overrightarrow {AE} = AB.AE\)
Tương tự ta có \(D\) nằm giữa hai điểm \(A\) và \(F.\) Suy ra \(\overrightarrow {AD} .\overrightarrow {AF} = AD.AF\)
Vậy \(\left( * \right)\) trở thành: \(AB.AE + AD.AF = A{C^2}\)
Chọn D.
Câu hỏi 36 :
Cho tam giác \(ABC\) vuông tại \(A\) có \(BC = 2a,M\) là điểm trên đoạn \(BC\) sao cho \(MB = 2MC.\) Biết \(\overrightarrow {AM} .\overrightarrow {BC} = {a^2}.\) Độ dài cạnh \(AC\) là:
- A \(AC = \frac{{a\sqrt {33} }}{3}\)
- B \(AC = a\sqrt 3 \)
- C \(AC = \frac{{a\sqrt 3 }}{3}\)
- D \(AC = a\sqrt 5 \)
Đáp án: A
Phương pháp giải:
Ta biến đổi tích vô hướng \(\overrightarrow {AM} .\overrightarrow {BC} \) theo \(\overrightarrow {AB} ,\overrightarrow {AC} \) rồi sau đó thay theo giả thiết cho kết quả
Lời giải chi tiết:
Từ giả thiết \(M\) là điểm nằm trên \(BC\) sao cho \(MB = 2MC\) nên ta có \(\overrightarrow {BM} = \frac{1}{3}\overrightarrow {BC} \)
Đặt \(AB = x,AC = y \Rightarrow {x^2} + {y^2} = 4{a^2}\,\,\,\,\left( 1 \right)\) (do \(\Delta ABC\) vuông tại \(A)\)
Mặt khác từ \(\overrightarrow {AM} = \overrightarrow {AB} + \overrightarrow {BM} = \overrightarrow {AB} + \frac{1}{3}\overrightarrow {BC} = \overrightarrow {AB} + \frac{1}{3}\left( {\overrightarrow {AC} - \overrightarrow {AB} } \right) = \frac{2}{3}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC} \)
\(\begin{array}{l} \Rightarrow \overrightarrow {AM} .\overrightarrow {BC} = {a^2} \Leftrightarrow \left( {\frac{2}{3}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC} } \right)\left( {\overrightarrow {AC} - \overrightarrow {AB} } \right) = {a^2}\\ \Leftrightarrow \frac{1}{3}{\overrightarrow {AC} ^2} - \frac{2}{3}{\overrightarrow {AB} ^2} = {a^2}\,\,\,\,\left( {do{\rm{ }}\overrightarrow {AB} .\overrightarrow {AC} = 0} \right)\\ \Leftrightarrow \frac{1}{3}{y^2} - \frac{2}{3}{x^2} = {a^2}\,\,\,\left( 2 \right)\end{array}\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) ta có \(y = \frac{{a\sqrt {33} }}{3}.\)
Chọn A
Câu hỏi 37 :
Trong không gian cho tam giác \(ABC\) có \(AB = 4,\,\,BC = 6,\,\,CA = 8\). Tìm tập hợp điểm \(M\) sao cho \(\left( {\overrightarrow {MA} + \overrightarrow {MB} } \right)\left( {\overrightarrow {MB} + \overrightarrow {MC} } \right) = 0\) là mặt cầu có đường kính bằng bao nhiêu?
- A Mặt cầu có đường kính bằng \(4\)
- B Mặt cầu có đường kính bằng \(2\)
- C Mặt cầu có đường kính bằng \(1\)
- D Mặt cầu có đường kính bằng \(3\)
Đáp án: A
Phương pháp giải:
Sử dụng công thức trung điểm: Gọi \(M\) là trung điểm của \(AB\), với mọi \(I\) ta có \(\overrightarrow {IA} + \overrightarrow {IB} = 2\overrightarrow {IM} \).
Lời giải chi tiết:
Gọi \(I,\,\,J\) lần lượt là trung điểm của \(AB,\,\,BC\) ta có:
\(\left\{ \begin{array}{l}\overrightarrow {MA} + \overrightarrow {MB} = 2\overrightarrow {MI} \\\overrightarrow {MB} + \overrightarrow {MC} = 2\overrightarrow {MJ} \end{array} \right.\) \( \Rightarrow \left( {\overrightarrow {MA} + \overrightarrow {MB} } \right)\left( {\overrightarrow {MB} + \overrightarrow {MC} } \right) = 4\overrightarrow {MI} .\overrightarrow {MJ} \).
\( \Rightarrow 4\overrightarrow {MI} .\overrightarrow {MJ} = 0 \Leftrightarrow MI \bot MJ \Rightarrow \angle IMJ = {90^0}\).
\( \Rightarrow \) Tập hợp các điểm \(M\) là mặt cầu đường kính \(IJ\).
Vì \(IJ\) là đường trung bình của tam giác \(ABC\) nên \(IJ = \dfrac{1}{2}AC = 4\).
Vậy hợp các điểm \(M\) là mặt cầu đường kính bằng \(4.\)
Chọn A.
Câu hỏi 38 :
Trong mặt phẳng toạ độ \(Oxy,\) cho tam giác \(ABC\) có \(A\left( { - 3;0} \right),B\left( {3;0} \right)\) và \(C\left( {2;6} \right)\). Gọi \(H\left( {a;b} \right)\) là toạ độ trực tâm của tam giác đã cho. Tính \(a + 6b.\)
- A \(a + 6b = 5\)
- B \(a + 6b = 6\)
- C \(a + 6b = 7\)
- D \(a + 6b = 8\)
Đáp án: C
Phương pháp giải:
+) Tích vô hướng của hai véc tơ \(\overrightarrow a \) và \(\overrightarrow b \) là: \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.c{\rm{os}}\left( {\overrightarrow a ,\overrightarrow b } \right)\)
+) \(\overrightarrow a \) vuông góc với \(\overrightarrow b \Leftrightarrow \overrightarrow a .\overrightarrow b = 0\)
Lời giải chi tiết:
Ta có \(\left\{ {\begin{array}{*{20}{c}}{\overrightarrow {AH} = \left( {a + 3;b} \right),\overrightarrow {BC} = \left( { - 1;6} \right)}\\{\overrightarrow {BH} = \left( {a - 3;b} \right),\overrightarrow {AC} = \left( {5;6} \right)}\end{array}} \right.\)
Từ giả thiết, ta có \(\left\{ {\begin{array}{*{20}{c}}{\overrightarrow {AH} .\overrightarrow {BC} = 0}\\{\overrightarrow {BH} .\overrightarrow {AC} = 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{\left( {a + 3} \right).\left( { - 1} \right) + b.6 = 0}\\{\left( {a - 3} \right).5 + b.6 = 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = 2}\\{b = \frac{5}{6}}\end{array} \Rightarrow a + 6b = 7} \right.} \right.} \right.\)
Chọn C.
Câu hỏi 39 :
Cho hình thoi ABCD có \(\angle BAD = {60^0}\) và BA = a. Gọi M, N lần lượt là trung điểm của AD, DC. Tính \(\overrightarrow {BM} .\overrightarrow {BN} \) bằng:
- A \(\frac{{3\sqrt 3 {a^2}}}{8}\)
- B \(\frac{{3{a^2}}}{8}\)
- C \(\frac{{3{a^2}}}{4}\)
- D
\(\frac{{\sqrt 3 {a^2}}}{4}\)
Đáp án: B
Phương pháp giải:
Sử dụng công thức tính tích vô hướng: \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\cos \left( {\overrightarrow a ,\,\,\overrightarrow b } \right).\)
Lời giải chi tiết:
Ta có: ABCD là hình thoi có \(\angle BAD = {60^0}\)\( \Rightarrow \angle ABC = {120^0}\) và tam giác ABD là tam giác đều.
\( \Rightarrow AB = AD = BD = a.\)
Áp dụng quy tắc hình bình hành ta có: \(\left\{ \begin{array}{l}\overrightarrow {BM} = \frac{1}{2}\left( {\overrightarrow {BA} + \overrightarrow {BD} } \right)\\\overrightarrow {BN} = \frac{1}{2}\left( {\overrightarrow {BD} + \overrightarrow {BC} } \right)\end{array} \right..\)
\(\begin{array}{l} \Rightarrow \overrightarrow {BM} .\overrightarrow {BN} = \frac{1}{4}\left( {\overrightarrow {BA} + \overrightarrow {BD} } \right)\left( {\overrightarrow {BD} + \overrightarrow {BC} } \right)\\ = \frac{1}{4}\left( {\overrightarrow {BA} .\overrightarrow {BD} + \overrightarrow {BA} .\overrightarrow {BC} + {{\overrightarrow {BD} }^2} + \overrightarrow {BD} .\overrightarrow {BC} } \right)\\ = \frac{1}{4}\left( {BA.BD.\cos ABD + BA.BC.\cos ABC + B{D^2} + BD.BC.\cos DBC} \right)\\ = \frac{1}{4}\left( {{a^2}.\cos {{60}^0} + {a^2}.\cos {{120}^0} + {a^2} + {a^2}.\cos {{60}^0}} \right)\\ = \frac{1}{4}\left( {\frac{{{a^2}}}{2} - \frac{{{a^2}}}{2} + {a^2} + \frac{{{a^2}}}{2}} \right) = \frac{{3{a^2}}}{8}.\end{array}\)
Đáp án B.
Câu hỏi 40 :
Trên hệ \((O;\overrightarrow i ,\overrightarrow j )\) cho các vectơ \(\overrightarrow u = (3; - 1),\overrightarrow v = (2;5)\). Khi đó, tích vô hướng của hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) bằng:
- A 1
- B 11
- C (5; 4)
- D (1; -6)
Đáp án: A
Phương pháp giải:
+) Sử dụng công thức tích vô hướng của hai vecto: \(\overrightarrow a = \left( {{a_1};{a_2}} \right);\,\,\overrightarrow b = \left( {{b_1};{b_2}} \right) \Rightarrow \overrightarrow a .\overrightarrow b = {a_1}.{b_1} + {a_2}.{b_2}\)
Lời giải chi tiết:
Ta có: \(\overrightarrow u .\overrightarrow v = 3.2 - 1.5 = 1.\)
Chọn A.
>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10
 |
 |
 |
 |
 |
 |
 |
 |
Các bài khác cùng chuyên mục