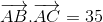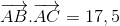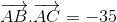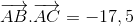40 bài tập trắc nghiệm về tích vô hướng của hai vectơ mức độ nhận biết, thông hiểu
Làm đề thiCâu hỏi 1 :
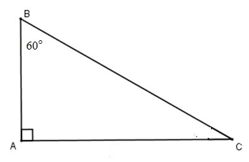
Cho ABC đều. Khi đó góc
ABC đều. Khi đó góc  có giá trị là:
có giá trị là:
- A 600
- B 300
- C 1200
- D Đáp án khác
Đáp án: C
Lời giải chi tiết:
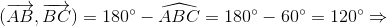 Chọn C
Chọn C
Câu hỏi 2 :
Trong mặt phẳng toạ độ, cho 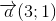 . Vectơ nào sau đây không vuông góc với vectơ
. Vectơ nào sau đây không vuông góc với vectơ 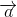 .
.
- A
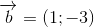
- B
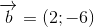
- C
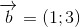
- D
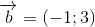
Đáp án: C
Lời giải chi tiết:
Ta có 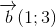 không vuông góc với
không vuông góc với 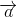 . Vì
. Vì 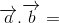 1.3+3.1=6#0
1.3+3.1=6#0
Chọn C.
Câu hỏi 3 :
Cho A(1;2); B(-2;-4); C(0;1); D(-1;\({3 \over 2}\)). Khẳng định nào sau đây đúng?
- A \(\overrightarrow {AB} \) cùng phương với \(\overrightarrow {CD} \).
- B \(\left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {CD} } \right|\)
- C \(\overrightarrow {AB} \bot \overrightarrow {CD} \)
- D \(\overrightarrow {AB} = \overrightarrow {CD} \)
Đáp án: C
Phương pháp giải:
- Tính \(\overrightarrow {AB} .\overrightarrow {CD} \) để kiểm tra 2 vector có vuông góc hay không?
- Hai vector \(\overrightarrow a \left( {{x_1},{y_1}} \right),\overrightarrow b = \left( {{x_2},{y_2}} \right) \Rightarrow \overrightarrow a = \overrightarrow b \Leftrightarrow \left\{ \matrix{ {x_1} = {x_2} \hfill \cr {y_1} = {y_2} \hfill \cr} \right..\)
- Hai vector \(\overrightarrow a ,\overrightarrow b \) được gọi là cùng phương khi và chỉ khi tồn tại hằng số \(k \ne 0\( sao cho \(\overrightarrow a = k\overrightarrow b .\)
Lời giải chi tiết:
Ta có: \(\overrightarrow {AB} = \left( { - 3; - 6} \right);\overrightarrow {CD} = \left( { - 1;{1 \over 2}} \right)\) nên \(\overrightarrow {AB} .\overrightarrow {CD} = \left( { - 3} \right).\left( { - 1} \right) + \left( { - 6} \right).{1 \over 2} = 0 \Rightarrow \overrightarrow {AB} \bot \overrightarrow {CD} .\)
Dễ thấy \({{ - 3} \over { - 1}} \ne {{ - 6} \over {{1 \over 2}}} \Rightarrow \overrightarrow {AB} ,\overrightarrow {CD} \) không cùng phương nên A sai.
\(\left| {\overrightarrow {AB} } \right| = \sqrt {{{\left( { - 3} \right)}^2} + {{\left( { - 6} \right)}^2}} = 3\sqrt 5 ,\left| {\overrightarrow {CD} } \right| = \sqrt {{{\left( { - 1} \right)}^2} + {{\left( {{1 \over 2}} \right)}^2}} = {{\sqrt 5 } \over 2} \Rightarrow \left| {\overrightarrow {AB} } \right| \ne \left| {\overrightarrow {CD} } \right|.\) Suy ra B sai.
Và dễ thấy D đương nhiên sai.
Chọn C.
Câu hỏi 4 :
Cho tam giác ABC với A(1;0); B(-2;-1) và C(0;3). Xác định hình dạng của tam giác ABC.
- A Đều
- B Vuông tại C
- C Vuông tại A
- D Cân tại B.
Đáp án: C
Phương pháp giải:
- Thiết lập tọa độ các vector\(\overrightarrow {AB} = \left( {{x_B} - {x_A},{y_B} - {y_A}} \right),\,\overrightarrow {AC} = \left( {{x_C} - {x_A},{y_C} - {y_A}} \right).\)
- Vận dụng công thức tính tích vô hướng hai vector: \(\overrightarrow u \left( {{x_1},{y_1}} \right),\overrightarrow v \left( {{x_2};{y_2}} \right) \Rightarrow \overrightarrow u .\overrightarrow v = {x_1}{x_2} + {y_1}{y_2}.\)
- Hai vector vuông góc có tích vô hướng bằng 0.
Lời giải chi tiết:
Ta có: \(\overrightarrow {AB} = \left( { - 2 - 1; - 1 - 0} \right) = \left( { - 3; - 1} \right)\,\,;\,\,\overrightarrow {AC} = \left( {0 - 1;3 - 0} \right) = \left( { - 1;3} \right)\) nên \(\overrightarrow {AB} .\overrightarrow {AC} = \left( { - 3} \right).\left( { - 1} \right) + \left( { - 1} \right).3 = 0\)
\( \Rightarrow AB \bot AC\) Tam giác ABC vuông tại A.
Chọn C.
Câu hỏi 5 :
Cho hai vectơ \(\overrightarrow a = \left( {4;3} \right),\overrightarrow b = \left( {1;7} \right)\). Góc giữa hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) là?
- A \({90^0}\)
- B \({60^0}\)
- C \({45^0}\)
- D \({30^0}\)
Đáp án: C
Phương pháp giải:
Sử dụng công thức\(c{\rm{os}}\left( {\overrightarrow a ;\overrightarrow b } \right) = {{\overrightarrow a .\overrightarrow b } \over {\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}}\)
Lời giải chi tiết:
\(c{\rm{os}}\left( {\overrightarrow a ;\overrightarrow b } \right) = {{\overrightarrow a .\overrightarrow b } \over {\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}} = {{4.1 + 3.7} \over {\sqrt {{4^2} + {3^2}} .\sqrt {{1^2} + {7^2}} }} = {{25} \over {\sqrt {25} .\sqrt {50} }} = {{\sqrt 2 } \over 2}\)
Chọn C.
Câu hỏi 6 :
Tích vô hướng của hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) được xác định bởi công thức:
- A \(\overrightarrow a .\overrightarrow b = \overrightarrow a .\overrightarrow b .\cos (\overrightarrow a ,\overrightarrow b )\)
- B \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos (\overrightarrow a ,\overrightarrow b )\)
- C \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\)
- D \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\sin (\overrightarrow a ,\overrightarrow b )\)
Đáp án: B
Phương pháp giải:
Sử dụng công thức tích vô hướng của 2 vectơ.
Lời giải chi tiết:
Tích vô hướng của 2 vecto \(\overrightarrow a ,\overrightarrow b \) được xác định bởi công thức \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ,\overrightarrow b } \right)\)
Chọn B.
Câu hỏi 7 :
Cho hai vecto \(\overrightarrow a = \left( {7; - 2} \right),\overrightarrow b = \left( {3; - 4} \right).\) Giá trị của \(\overrightarrow a .\overrightarrow b \) là:
- A 29
- B 13
- C -26
- D \(5\sqrt {33}\)
Đáp án: A
Phương pháp giải:
\(\overrightarrow a \left( {{x_1};{y_1}} \right),\overrightarrow b \left( {{x_2},{y_2}} \right) \Rightarrow \overrightarrow a .\overrightarrow b = {x_1}{x_2} + {y_1}{y_2}.\)
Lời giải chi tiết:
\(\overrightarrow a .\overrightarrow b = 7.3 + \left( { - 2} \right)\left( { - 4} \right) = 29.\)
Chọn A.
Câu hỏi 8 :
Cho tam giác ABC vuông cân tại A có BC =2. Tính tích vô hướng \(\overrightarrow {AB} .\overrightarrow {CA} \) :
- A 0
- B -4.
- C 2
- D 4
Đáp án: A
Lời giải chi tiết:
Vì \(AB \bot AC\) nên \(\overrightarrow {AB} .\overrightarrow {CA} = 0\).
Chọn: A
Câu hỏi 9 :
Cho hình vuông ABCD. Khi đó cos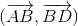 có giá trị là:
có giá trị là:
- A
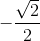
- B
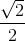
- C
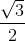
- D Đáp án khác
Đáp án: A
Lời giải chi tiết:
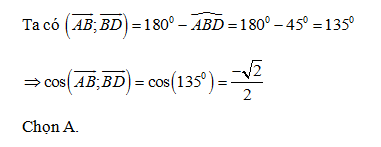
Câu hỏi 10 :
Trong mặt phẳng toạ độ \(Oxy,\) cho ba véc tơ \(\overrightarrow a = \left( {1;2} \right),\overrightarrow b = \left( {4;3} \right)\) và \(\overrightarrow c = \left( {2;3} \right).\) Tính \(P = \overrightarrow a .\left( {\overrightarrow b + \overrightarrow c } \right)\)
- A \(P = 0\)
- B \(P = 20\)
- C \(P = 28\)
- D \(P = 18\)
Đáp án: D
Phương pháp giải:
\(\overrightarrow a = \left( {{a_1};{a_2}} \right),\overrightarrow b = \left( {{b_1};{b_2}} \right)\)
Tích vô hướng của \(\overrightarrow a \) và \(\overrightarrow b \) được tính như sau: \(\overrightarrow a .\overrightarrow b = {a_1}{b_1} + {a_2}{b_2}\)
Lời giải chi tiết:
Ta có \(\overrightarrow b + \overrightarrow c = \left( {6;6} \right)\)
Suy ra \(P = \overrightarrow a .\left( {\overrightarrow b + \overrightarrow c } \right) = 1.6 + 2.6 = 18\)
Chọn D.
Câu hỏi 11 :
Cho hai vecto \(\overrightarrow a ,\overrightarrow b \) thoả mãn \(\left| {\overrightarrow a } \right| = 3,\left| {\overrightarrow b } \right| = 2\) và \(\overrightarrow a .\overrightarrow b = - 3.\) Xác định góc \(\alpha \) giữa hai vecto \(\overrightarrow a ,\overrightarrow b \)?
- A \({30^0}\)
- B \({45^0}\)
- C \({60^0}\)
- D \({120^0}\)
Đáp án: D
Phương pháp giải:
Tích vô hướng của hai véc tơ \(\overrightarrow a \) và \(\overrightarrow b \) là: \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.c{\rm{os}}\left( {\overrightarrow a ,\overrightarrow b } \right)\)
Lời giải chi tiết:
Ta có \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.c{\rm{os}}\left( {\overrightarrow a ,\overrightarrow b } \right)\) nên \(c{\rm{os}}\left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}} = \frac{{ - 3}}{{3.2}} = - \frac{1}{2} \Rightarrow \left( {\overrightarrow a ,\overrightarrow b } \right) = {120^0}\)
Chọn D.
Câu hỏi 12 :
Cho hai véc tơ \(\overrightarrow a \) và \(\overrightarrow b \) thoả mãn \(\left| {\overrightarrow a } \right| = \left| {\overrightarrow b } \right| = 1\) và hai véc tơ \(\overrightarrow u = \frac{2}{5}\overrightarrow a - 3\overrightarrow b \) và \(\overrightarrow v = \overrightarrow a + \overrightarrow b \) vuông góc với nhau. Xác định góc \(\alpha \) giữa \(\overrightarrow a \) và \(\overrightarrow b \)?
- A \(\alpha = {90^0}\)
- B \(\alpha = {180^0}\)
- C \(\alpha = {60^0}\)
- D \(\alpha = {45^0}\)
Đáp án: B
Phương pháp giải:
+) Tích vô hướng của hai véc tơ \(\overrightarrow a \) và \(\overrightarrow b \) là: \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.c{\rm{os}}\left( {\overrightarrow a ,\overrightarrow b } \right)\)
+) \(\overrightarrow a \) vuông góc với \(\overrightarrow b \Leftrightarrow \overrightarrow a .\overrightarrow b = 0\)
Lời giải chi tiết:
Ta có: \(\overrightarrow u \bot \overrightarrow v \Rightarrow \left( {\frac{2}{5}\overrightarrow a - 3\overrightarrow b } \right)\left( {\overrightarrow a + \overrightarrow b } \right) = 0 \Leftrightarrow \frac{2}{5}{\overrightarrow a ^2} - \frac{{13}}{5}\overrightarrow a \overrightarrow b - 3{\overrightarrow b ^2} = 0 \Leftrightarrow - \frac{{13}}{5} - \frac{{13}}{5}\overrightarrow a \overrightarrow b = 0 \Leftrightarrow \overrightarrow a .\overrightarrow b = - 1\)
\( \Rightarrow \cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}} = \frac{{ - 1}}{{1.1}} = - 1 \Rightarrow \left( {\overrightarrow a ,\overrightarrow b } \right) = {180^0}.\)
Chọn B.
Câu hỏi 13 :
Trong mặt phẳng toạ độ \(Oxy,\)cho tam giác \(ABC\) có \(A\left( {1;4} \right),B\left( {3;2} \right),C\left( {5;4} \right).\)Tính chu vi \(P\) tam giác \(ABC?\)
- A \(P = 4 + 2\sqrt 2 \)
- B \(P = 4 + 4\sqrt 2 \)
- C \(P = 8 + 8\sqrt 2 \)
- D \(P = 2 + 2\sqrt 2 \)\(\)
Đáp án: B
Phương pháp giải:
Cho \(\overrightarrow a = \left( {{a_1};{a_2}} \right) \Rightarrow \left| {\overrightarrow a } \right| = \sqrt {{a_1}^2 + {a_2}^2} .\)
Lời giải chi tiết:
Ta có: \(\left\{ {\begin{array}{*{20}{c}}{\overrightarrow {AB} = \left( {2; - 2} \right)}\\{\overrightarrow {BC} = \left( {2;2} \right)}\\{\overrightarrow {CA} = \left( { - 4;0} \right)}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{c}}{AB = \sqrt {{2^2} + {{\left( { - 2} \right)}^2}} = 2\sqrt 2 }\\{BC = \sqrt {{2^2} + {2^2}} = 2\sqrt 2 }\\{CA = \sqrt {{{\left( { - 4} \right)}^2} + {0^2}} = 4}\end{array}} \right.} \right.\)
Vậy chu vi \(P\) của tam giác \(ABC\) là \(P = AB + BC + CA = 4 + 4\sqrt 2 .\)
Chọn B.
Câu hỏi 14 :
Cho \(\overrightarrow a = \left( {1;2} \right),\,\,\overrightarrow b = \left( { - 1;3} \right).\) Tính \(\overrightarrow a .\overrightarrow b ?\)
- A \(6\)
- B \(5\)
- C \(4\)
- D \(3\)
Đáp án: B
Phương pháp giải:
Cho \(\overrightarrow a = \left( {{x_1},{y_1}} \right),\overrightarrow b = \left( {{x_2},{y_2}} \right)\). Khi đó \(\overrightarrow a .\overrightarrow b = {x_1}{x_2} + {y_1}{y_2}\).
Lời giải chi tiết:
Ta có: \(\overrightarrow a = \left( {1;2} \right),\,\overrightarrow b = \left( { - 1;3} \right)\)\( \Rightarrow \overrightarrow a .\overrightarrow b = 1.\left( { - 1} \right) + 2.3 = 5\).
Chọn B.
Câu hỏi 15 :
Cho \(\overrightarrow a = \left( {2; - 1} \right),\overrightarrow b \left( {3; - 5} \right),\overrightarrow c = \left( { - 1; - 3} \right).\) Giá trị của biểu thức \(\overrightarrow a \left( {\overrightarrow b - \overrightarrow c } \right)\)
- A \(10\)
- B \(12\)
- C \(16\)
- D \(8\)
Đáp án: A
Phương pháp giải:
Dùng công thức tích vô hướng của hai vectơ: \(\overrightarrow {a\,} \left( {{a_1};\,\,{a_2}} \right),\,\,\,\overrightarrow b = \left( {{b_1};\,\,{b_2}} \right) \Rightarrow \overrightarrow a .\overrightarrow b = {a_1}{b_1} + {a_2}{b_2}.\)
Lời giải chi tiết:
Ta có: \(\overrightarrow b - \overrightarrow c = \left( {3 + 1; - 5 + 3} \right) = \left( {4; - 2} \right).\)
\( \Rightarrow \overrightarrow a \left( {\overrightarrow b - \overrightarrow c } \right) = \left( {2; - 1} \right)\left( {4; - 2} \right) = 2.4 + \left( { - 1} \right).\left( { - 2} \right) = 10.\)
Chọn A.
Câu hỏi 16 :
Cho tam giác ABC vuông tại A và có \(\widehat {ABC} = 40^\circ .\) Tính góc giữa hai vectơ \(\overrightarrow {CA} \) và \(\overrightarrow {CB} .\)
- A \(\left( {\overrightarrow {CA} ,\overrightarrow {CB} } \right) = 40^\circ .\)
- B \(\left( {\overrightarrow {CA} ,\overrightarrow {CB} } \right) = 130^\circ .\)
- C \(\left( {\overrightarrow {CA} ,\overrightarrow {CB} } \right) = 140^\circ .\)
- D \(\left( {\overrightarrow {CA} ,\overrightarrow {CB} } \right) = 50^\circ .\)
Đáp án: D
Phương pháp giải:
Định lý về tổng ba góc trong một tam giác.
Lời giải chi tiết:
Tam giác ABC vuông tại A và có \(\widehat {ABC} = 40^\circ \Rightarrow \widehat {ACB} = 50^\circ \Rightarrow \left( {\overrightarrow {CA} ,\overrightarrow {CB} } \right) = 50^\circ .\)
Chọn D.
Câu hỏi 17 :
Trong mặt phẳng toạ độ \(Oxy,\)cho hai vecto \(\overrightarrow u = \frac{1}{2}\overrightarrow i - 5\overrightarrow j \) và \(\overrightarrow v = k\overrightarrow i - 4\overrightarrow j .\) Tìm \(k\) để \(\overrightarrow u \bot \overrightarrow v ?\)
- A \(k = 20\)
- B \(k = - 20\)
- C \(k = - 40\)
- D \(k = 40\)
Đáp án: C
Phương pháp giải:
Cho \(\overrightarrow a = \left( {{a_1};{a_2}} \right),\overrightarrow b = \left( {{b_1};{b_2}} \right).\) Khi đó: \(\overrightarrow a \bot \overrightarrow b \Leftrightarrow \overrightarrow a .\overrightarrow b = 0 \Leftrightarrow {a_1}{b_1} + {a_2}{b_2} = 0.\)
Lời giải chi tiết:
Từ giả thiết ta suy ra \(\overrightarrow u = \left( {\frac{1}{2}; - 5} \right),\overrightarrow v = \left( {k; - 4} \right)\)
\( \Rightarrow \overrightarrow u \bot \overrightarrow v \Leftrightarrow \frac{1}{2}k + \left( { - 5} \right)\left( { - 4} \right) = 0 \Leftrightarrow \frac{1}{2}k = - 20 \Leftrightarrow k = - 40\)
Chọn C.
Câu hỏi 18 :
Trong mặt phẳng toạ độ \(Oxy,\) cho ba điểm \(A\left( {3; - 1} \right),B\left( {2;10} \right),C\left( { - 4;2} \right).\) Tính \(\overrightarrow {AB} .\overrightarrow {AC} ?\)
- A \(\overrightarrow {AB} .\overrightarrow {AC} = 40\)
- B \(\overrightarrow {AB} .\overrightarrow {AC} = - 40\)
- C \(\overrightarrow {AB} .\overrightarrow {AC} = 26\)
- D \(\overrightarrow {AB} .\overrightarrow {AC} = - 26\)
Đáp án: A
Phương pháp giải:
\(\overrightarrow a = \left( {{a_1};{a_2}} \right),\overrightarrow b = \left( {{b_1};{b_2}} \right) \Rightarrow \overrightarrow a .\overrightarrow b = {a_1}{b_1} + {a_2}{b_2}.\)
Lời giải chi tiết:
Ta có: \(\overrightarrow {AB} = \left( { - 1;\,\,11} \right),\overrightarrow {AC} = \left( { - 7;\,\,3} \right) \Rightarrow \overrightarrow {AB} .\overrightarrow {AC} = \left( { - 1} \right)\left( { - 7} \right) + 11.3 = 40\)
Chọn A.
Câu hỏi 19 :
Cho hình vuông \(ABCD\) cạnh \(a.\) Khi đó \(\overrightarrow {AB} .\overrightarrow {AC} \) bằng:
- A \({a^2}\)
- B \({a^2}\sqrt 2 \)
- C \(\frac{{\sqrt 2 }}{2}{a^2}\)
- D \(\frac{1}{2}{a^2}\)
Đáp án: A
Phương pháp giải:
Tích vô hướng của hai véc tơ \(\overrightarrow a \) và \(\overrightarrow b \) là: \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.c{\rm{os}}\left( {\overrightarrow a ,\overrightarrow b } \right)\)
Lời giải chi tiết:
Ta có \(\left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = {45^o},AC = a\sqrt 2 \) nên \(\overrightarrow {AB} .\overrightarrow {AC} = AB.AC.c{\rm{os4}}{{\rm{5}}^o} = a.a\sqrt 2 .\frac{{\sqrt 2 }}{2} = {a^2}.\)
Chọn A.
Câu hỏi 20 :
Cho hình vuông ABCD cạnh bằng a. Tích vô hướng \(\overrightarrow {AC} .\overrightarrow {CB} \) là:
- A \( - \frac{{{a^2}}}{2}\)
- B \({a^2}\)
- C \( - {a^2}\)
- D \(\frac{{{a^2}}}{2}\)
Đáp án: C
Phương pháp giải:
Sử dụng định nghĩa tích vô hướng của 2 vecto \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ,\overrightarrow b } \right).\)
Lời giải chi tiết:
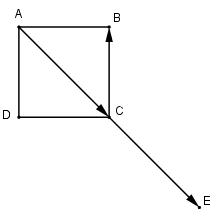
Đưa về 2 vector chung gốc để tìm góc giữa hai vector ta có
\(\left( {\overrightarrow {AC} ,\overrightarrow {CB} } \right) = \left( {\overrightarrow {CE} ,\overrightarrow {CB} } \right) = \widehat {ECB} = {180^0} - \widehat {ACB} = {180^0} - {45^0} = {135^0}.\)
\(\Rightarrow \overrightarrow {AC} .\overrightarrow {CB} = \left| {\overrightarrow {AC} } \right|.\left| {\overrightarrow {CB} } \right|.\cos \left( {\overrightarrow {AC} ,\overrightarrow {CB} } \right) = a\sqrt 2 .a.cos{135^0} = a\sqrt 2 .a.\left( { - \frac{{\sqrt 2 }}{2}} \right) = - {a^2}.\)
Chọn C.
Câu hỏi 22 :
Cho tam giác ABC đều cạnh AB=6cm. Gọi M là một điểm trên cạnh AC sao cho AM= AC.Khi đó
AC.Khi đó 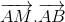 bằng:
bằng:
- A 30
- B -6
- C 2
- D 6
Đáp án: D
Lời giải chi tiết:
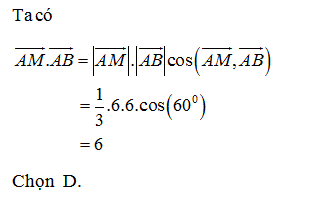
Câu hỏi 23 :
Cho tam giác ABC có A(1;3), B(5;-4), C(-3;-2). Gọi G là trọng tâm tam giác ABC. Giá trị 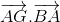 bằng:
bằng:
- A 21
- B 14
- C 28
- D -28
Đáp án: D
Lời giải chi tiết:

Chọn D
Câu hỏi 24 :
Cho hình vuông ABCD có cạnh a. Tìm đáp án đúng nhất.
- A \(\overrightarrow {AB} .\overrightarrow {AD} = 0;\overrightarrow {AB} .\overrightarrow {AC} = 0\)
- B \(\overrightarrow {AB} .\overrightarrow {AD} = 0;\overrightarrow {AB} .\overrightarrow {AC} = {a^2}\)
- C \(\overrightarrow {AB} .\overrightarrow {AD} = {a^2};\overrightarrow {AB} .\overrightarrow {AC} = 0\)
- D \(\overrightarrow {AB} .\overrightarrow {AD} = {a^2};\overrightarrow {AB} .\overrightarrow {AC} = {a^2}\)
Đáp án: B
Phương pháp giải:
Vận dụng công thức định nghĩa tính tích vô hướng hai vector.
Hai vector \(\overrightarrow u .\overrightarrow v = \left| {\overrightarrow u } \right|.\left| {\overrightarrow v } \right|.\cos \left( {\overrightarrow u ,\overrightarrow v } \right).\)
Hai vector vuông góc thì tích vô hướng của chúng bằng 0.
Lời giải chi tiết:
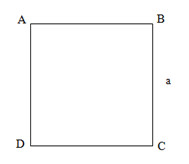
Vì \(AB \bot AD\) nên \(\overrightarrow {AB} .\overrightarrow {AD} = 0 \Rightarrow \) C và D sai.
AC là đường chéo của hình vuông nên \(AC = a\sqrt 2 ,\left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = {45^0}\)
\( \Rightarrow \overrightarrow {AB} .\overrightarrow {AC} = AB.AC.c{\rm{os}}\left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = a.a\sqrt 2 .{1 \over {\sqrt 2 }} = {a^2}\). Suy ra đáp án A sai
Vậy đáp án B đúng.
Chọn B.
Câu hỏi 25 :
Cho hai vectơ \(\overrightarrow a = \left( { - 2; - 2\sqrt 3 } \right),\overrightarrow b = (3;\sqrt 3 )\).Góc giữa hai vectơ \(\overrightarrow a ,\overrightarrow b\) là?
- A \({90^0}\)
- B \({150^0}\)
- C \({45^0}\)
- D \({120^0}\)
Đáp án: B
Phương pháp giải:
Công thức tính cosin của góc giữa hai vecto \(\overrightarrow a \) và \(\overrightarrow b \) là: \(\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}}\)
Lời giải chi tiết:
\(\begin{array}{l}\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}} = \frac{{ - 2.3 - 2\sqrt 3 .\sqrt 3 }}{{\sqrt {4 + 12} .\sqrt {9 + 3} }} = \frac{{ - 12}}{{8\sqrt 3 }} = - \frac{{\sqrt 3 }}{2}\\ \Rightarrow \left( {\overrightarrow a ,\overrightarrow b } \right) = {150^0}.\end{array}\)
Chọn B.
Câu hỏi 26 :
Cho tam giác ABC biết \(AB = 5cm,BC = 7cm,CA = 8cm\). Khi đó \(\overrightarrow {AB} .\overrightarrow {AC} \) bằng
- A 5
- B 10
- C 15
- D 20
Đáp án: D
Phương pháp giải:
Công thức tính cosin của góc giữa hai vectơ \(\overrightarrow a \) vả \(\overrightarrow b \) lạ: \(\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}}\)
Lời giải chi tiết:
Áp dụng định lí cosin trong tam giác ABC ta có: \(\cos \widehat {BAC} = \frac{{A{B^2} + A{C^2} - B{C^2}}}{{2AB.AC}} = \frac{{{5^2} + {8^2} - {7^2}}}{{2.5.8}} = \frac{1}{2}.\)
Mà
\(\begin{array}{l}\left| {\cos \left( {\overrightarrow {AB} ;\overrightarrow {AC} } \right)} \right| = \cos \widehat {BAC} = \frac{1}{2}\\ \Leftrightarrow \frac{{\left| {\overrightarrow {AB} .\overrightarrow {AC} } \right|}}{{AB.AC}} = \frac{1}{2} \Leftrightarrow \left| {\overrightarrow {AB} .\overrightarrow {AC} } \right| = 5.8.\frac{1}{2} = 20.\end{array}\)
Chọn D
Câu hỏi 27 :
Cho hình vuông ABCD có cạnh bằng 1. Tính giá trị của biểu thức \(P = \left( {\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} } \right).\left( {\overrightarrow {BA} + \overrightarrow {BC} } \right)\) .
- A 0
- B 8
- C 16
- D \(4\sqrt 2 .\)
Đáp án: A
Lời giải chi tiết:
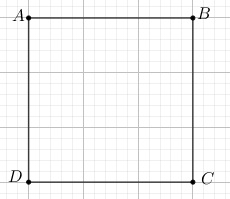
Ta có:
\(\begin{array}{l}P = \left( {\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} } \right).\left( {\overrightarrow {BA} + \overrightarrow {BC} } \right)\\ = 2\overrightarrow {AC} .\overrightarrow {BD} \\ = 0\end{array}\)
Chọn A.
Câu hỏi 28 :
Cho tam giác ABC đều, AB = 2 ; tam giác ABC nội tiếp đường tròn (O) . Tính giá trị của \(P = \overrightarrow {OA} .\left( {\overrightarrow {OB} + \overrightarrow {OC} } \right)\) .
- A 1
- B \( - \frac{4}{3}.\)
- C \(\frac{3}{4}.\)
- D \(\frac{2}{3}.\)
Đáp án: B
Lời giải chi tiết:
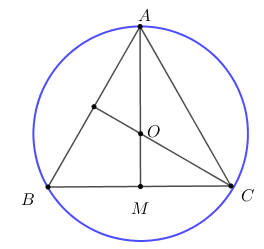
+) Ta có: AB = 2 \( \Rightarrow AM = \frac{{2.\sqrt 3 }}{2} = \sqrt 3 .\)
\(OA = \frac{2}{3}AM = \frac{2}{3}.AM = \frac{2}{3}.\sqrt 3 = \frac{2}{{\sqrt 3 }}.\)
+) \(\overrightarrow {OA} .\left( {\overrightarrow {OB} + \overrightarrow {OC} } \right) = 2\overrightarrow {OA} .\overrightarrow {OM} = - O{A^2} = \frac{{ - 4}}{3}\)
Chọn B.
Câu hỏi 29 :
Cho tam giác ABC vuông tại A, có số đo góc B là \(60^\circ \) và \(AB = a\). Kết quả nào sau đây là sai?
- A \(\overrightarrow {AB} .\overrightarrow {AC} = 0\).
- B \(\overrightarrow {CA} .\overrightarrow {CB} = 3{a^2}\).
- C \(\overrightarrow {AB} .\overrightarrow {BC} = - {a^2}\).
- D \(\overrightarrow {AC} .\overrightarrow {CB} = - 3\sqrt 2 a\).
Đáp án: D
Phương pháp giải:
\(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ;\overrightarrow b } \right)\).
Lời giải chi tiết:
Do \(AB \bot AC \Rightarrow \overrightarrow {AB} .\overrightarrow {AC} = 0\)
Tam giác ABC vuông tại A, góc B là \(60^\circ \) và \(AB = a\)
\( \Rightarrow AC = AB\tan 60^\circ = a\sqrt 3 ,\,\,BC = \frac{{AB}}{{\cos 60^\circ }} = \frac{a}{{\frac{1}{2}}} = 2a\)
Ta có:
\(\overrightarrow {CA} .\overrightarrow {CB} = CA.CB.\cos \left( {\overrightarrow {CA} ;\overrightarrow {CB} } \right) = a\sqrt 3 .2a.\cos 30^\circ = a\sqrt 3 .2a.\frac{{\sqrt 3 }}{2} = 3{a^2}\)
\(\overrightarrow {AB} .\overrightarrow {BC} = AB.BC.\cos \left( {\overrightarrow {AB} ;\overrightarrow {BC} } \right) = a.2a.\cos 120^\circ = 2{a^2}.\frac{{ - 1}}{2} = - {a^2}\)
\(\overrightarrow {AC} .\overrightarrow {CB} = - \overrightarrow {CA} .\overrightarrow {CB} = - 3{a^2} \ne - 3\sqrt 2 a\).
Chọn: D
Câu hỏi 30 :
Trong mặt phẳng Oxy cho \(A\left( {4;6} \right),\,B\left( {1;4} \right)\) và \(C\left( {7;\frac{3}{2}} \right)\). Ta có khẳng định nào sau đây là đúng?
- A \(\left( {\overrightarrow {AB} ;\overrightarrow {AC} } \right) < 90^\circ \).
- B \(\left( {\overrightarrow {AB} ;\overrightarrow {AC} } \right) = 90^\circ \).
- C \(\left( {\overrightarrow {AB} ;\overrightarrow {AC} } \right) = 180^\circ \).
- D \(\left( {\overrightarrow {AB} ;\overrightarrow {AC} } \right) = 0^\circ \).
Đáp án: B
Phương pháp giải:
Công thức xác định góc giữa hai vectơ: \(\cos \left( {\overrightarrow a ;\overrightarrow b } \right) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}}\).
Chú ý: \(\overrightarrow a .\overrightarrow b = 0 \Rightarrow \overrightarrow a \bot \overrightarrow b \).
Lời giải chi tiết:
\(\overrightarrow {AB} = \left( { - 3; - 2} \right),\,\,\overrightarrow {AC} = \left( {3; - \frac{9}{2}} \right)\) \( \Rightarrow \overrightarrow {AB} .\overrightarrow {AC} = - 3.3 + \left( { - 2} \right).\left( { - \frac{9}{2}} \right) = 0 \Rightarrow \left( {\overrightarrow {AB} ;\overrightarrow {AC} } \right) = 90^\circ \).
Chọn: B
Câu hỏi 31 :
Cho tam giác \(ABC\) với \(\widehat A = {60^0}\). Tính tổng \(\left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right) + \left( {\overrightarrow {BC} ,\overrightarrow {CA} } \right).\)
- A \({120^0}.\)
- B \({360^0}.\)
- C \({270^0}.\)
- D \({240^0}.\)
Đáp án: D
Phương pháp giải:
Xác định \(\left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right);\,\,\left( {\overrightarrow {BC} ,\overrightarrow {CA} } \right).\)
Lời giải chi tiết:
\(\begin{array}{l}\left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right) + \left( {\overrightarrow {BC} ,\overrightarrow {CA} } \right) = \widehat {CBx} + \widehat {BCy}\\ = {180^0} - \widehat {ABC} + {180^0} - \widehat {ACB} = {360^0} - \left( {\widehat {ABC} + \widehat {ACB}} \right)\\ = {360^0} - \left( {{{180}^0} - {{60}^0}} \right) = {240^0}\end{array}\)
Chọn D.
Câu hỏi 32 :
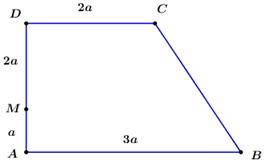
Cho hình thang ABCD vuông tại A và D, \(AB = 3a\), \(CD = 2a\), \(AD = 3a\), gọi M là điểm thuộc cạnh AD sao cho \(MA = a\). Tích \(\left( {\overrightarrow {MB} + \overrightarrow {MC} } \right).\overrightarrow {AB} \) bằng:
- A \( - 4{a^2}\)
- B \(16{a^2}\)
- C \( - 8{a^2}\)
- D \(15{a^2}\)
Đáp án: D
Phương pháp giải:
Sử dụng các tính chất và các công thức trong phép tính vectơ:
\(\begin{array}{l}
\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {BC} \\
AB//CD \Rightarrow \left[ \begin{array}{l}
\left( {\overrightarrow {AB} ,\;\overrightarrow {DC} } \right) = {0^0}\\
\left( {\overrightarrow {AB} ,\;\overrightarrow {CD} } \right) = {180^0}
\end{array} \right..\\
\overrightarrow a \bot \overrightarrow b \Rightarrow \overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = 0.
\end{array}\)
Lời giải chi tiết:
\(\begin{array}{l}\left( {\overrightarrow {MB} + \overrightarrow {MC} } \right).\overrightarrow {AB} = \left( {\overrightarrow {MA} + \overrightarrow {AB} + \overrightarrow {MD} + \overrightarrow {DC} } \right).\overrightarrow {AB} \\ = \overrightarrow {MA} .\overrightarrow {AB} + {\overrightarrow {AB} ^2} + \overrightarrow {MD} .\overrightarrow {AB} + \overrightarrow {DC} .\overrightarrow {AB} \\ = 0 + {\left| {\overrightarrow {AB} } \right|^2} + 0 + \left| {\overrightarrow {DC} } \right|.\left| {\overrightarrow {AB} } \right|.\cos \left( {\overrightarrow {DC} ,\overrightarrow {AB} } \right)\\ = {\left( {3a} \right)^2} + 2a.3a.\cos {0^o} = 9{a^2} + 6{a^2} = 15{a^2}.\end{array}\)
Chọn D.
Câu hỏi 33 :
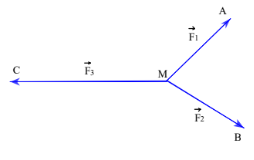
Cho ba lực \(\overrightarrow {{F_1}} = \overrightarrow {MA} ,\,\,\overrightarrow {{F_2}} = \overrightarrow {MB} ,\,\,\overrightarrow {{F_3}} = \overrightarrow {MC} \) cùng điểm đặt M , cùng tác động vào một vật và vật đó đứng yên (như hình vẽ). Biết cường độ của \(\overrightarrow {{F_1}} ,\,\,\overrightarrow {{F_2}} \) đều bằng 30N và \(\widehat {AMB} = {60^0}\). Tính cường độ lực \(\overrightarrow {{F_3}} \) là:
- A \(60N\)
- B \(30\sqrt 3 N\)
- C \(30\sqrt 2 N\)
- D \(15\sqrt 3 N\)
Đáp án: B
Phương pháp giải:
Sử dụng công thức tính độ dài của lực tổng hợp: \(F = \sqrt {F_1^2 + F_2^2 + 2{F_1}{F_2}\cos \alpha } \).
Lời giải chi tiết:
Do vật đứng yên \( \Rightarrow \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = \overrightarrow 0 \Rightarrow \overrightarrow {{F_3}} = - \left( {\overrightarrow {{F_1}} + \overrightarrow {{F_2}} } \right) \Rightarrow \left| {\overrightarrow {{F_3}} } \right| = \left| {\overrightarrow {{F_1}} + \overrightarrow {{F_2}} } \right|\).
Ta có \({\left| {\overrightarrow {{F_1}} + \overrightarrow {{F_2}} } \right|^2} = {\left| {\overrightarrow {{F_1}} } \right|^2} + {\left| {\overrightarrow {{F_2}} } \right|^2} + 2\left| {\overrightarrow {{F_1}} } \right|\left| {\overrightarrow {{F_2}} } \right|.\cos \widehat {AMB} = {30^2} + {30^2} + {2.30^2}.\cos {60^0} = 2700\)
\( \Rightarrow \left| {\overrightarrow {{F_1}} + \overrightarrow {{F_2}} } \right| = 30\sqrt 3 N \Rightarrow \left| {\overrightarrow {{F_3}} } \right| = 30\sqrt 3 N\).
Chọn B.
Câu hỏi 34 :
Cho hình thang vuông \(ABCD\) có đáy lớn \(AB = 4a,\) đáy nhỏ \(CD = 2a,\) đường cao\(AD = 3a;\) \(I\) là trung điểm của \(AD.\) Tích \(\left( {\overrightarrow {IA} + \overrightarrow {IB} } \right)\overrightarrow {ID} \) bằng?
- A \(\frac{{9{a^2}}}{2}\)
- B \( - \frac{{9{a^2}}}{2}\)
- C \(0\)
- D \(9{a^2}\)
Đáp án: B
Phương pháp giải:
Tích vô hướng của hai véc tơ \(\overrightarrow a \) và \(\overrightarrow b \) là: \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.c{\rm{os}}\left( {\overrightarrow a ,\overrightarrow b } \right)\)
Lời giải chi tiết:
Ta có \(\overrightarrow {IA} .\overrightarrow {ID} = - {\overrightarrow {IA} ^2} = - I{A^2}\)
Lại có: \(\overrightarrow {IB} .\overrightarrow {ID} = - IB.ID.c{\rm{os}}\angle BID = - IB.ID.\frac{{IA}}{{IB}} = - IA.ID = - I{A^2}\)
Vậy \(\left( {\overrightarrow {IA} + \overrightarrow {IB} } \right).\overrightarrow {ID} = \overrightarrow {IA} .\overrightarrow {ID} + \overrightarrow {IB} .\overrightarrow {ID} = - 2I{A^2} = - 2.\left( {\frac{{3{a^2}}}{2}} \right) = \frac{{ - 9{a^2}}}{2}\)
Chọn B.
Câu hỏi 35 :
Tam giác \(ABC\) có \(AB = c,BC = a,CA = b.\) Các cạnh \(a,b,c\) liên hệ với nhau bởi đẳng thức \(b\left( {{b^2} - {a^2}} \right) = c\left( {{a^2} - {c^2}} \right).\) Khi đó góc \(\angle BAC\) bằng bao nhiêu độ?
- A \({30^o}\)
- B \({45^o}\)
- C \({60^o}\)
- D \({90^o}\)
Đáp án: C
Phương pháp giải:
Sử dụng định lí cosin để đưa ra công thức tính cosin góc \(\angle BAC.\)
Sau đó, biến đổi đẳng thức \(b\left( {{b^2} - {a^2}} \right) = c\left( {{a^2} - {c^2}} \right)\)để xét mối liên hệ giữa các đại lượng \(a,b,c\) dựa vào các định lí trong tam giác.
Lời giải chi tiết:
Theo định lí hàm cosin, ta có: \(\cos \angle BAC = \frac{{A{B^2} + A{C^2} - B{C^2}}}{{2.AB.AC}} = \frac{{{c^2} + {b^2} - {a^2}}}{{2bc}}\)
Mà
\(\begin{array}{l}b\left( {{b^2} - {a^2}} \right) = c\left( {{a^2} - {c^2}} \right)\\ \Leftrightarrow {b^3} - {a^2}b = {a^2}c - {c^3}\\ \Leftrightarrow - {a^2}\left( {b + c} \right) + \left( {{b^3} + {c^3}} \right) = 0\\ \Leftrightarrow \left( {b + c} \right)\left( {{b^2} + {c^2} - {a^2} - bc} \right) = 0\\ \Leftrightarrow {b^2} + {c^2} - {a^2} - bc = 0\left( {do{\rm{ }}b > 0,c > 0} \right)\\ \Leftrightarrow {b^2} + {c^2} - {a^2} = bc\end{array}\)
Khi đó, \(\cos \angle BAC = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}} = \frac{1}{2} \Rightarrow \angle BAC = {60^o}\)
Chọn C.
Câu hỏi 36 :
Cho \(\overrightarrow a ,\overrightarrow b \) có \(\left( {\overrightarrow a + 2\overrightarrow b } \right)\) vuông góc với vecto \(\left( {5\overrightarrow a - 4\overrightarrow b } \right)\) và \(\left| {\overrightarrow a } \right| = \left| {\overrightarrow b } \right|.\) Khi đó:
- A \({\rm{cos}}\left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{\sqrt 2 }}{2}.\)
- B \({\rm{cos}}\left( {\overrightarrow a ,\overrightarrow b } \right) = 0.\)
- C \({\rm{cos}}\left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{\sqrt 3 }}{2}.\)
- D \({\rm{cos}}\left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{1}{2}.\)
Đáp án: D
Phương pháp giải:
+) \(\overrightarrow a \) vuông góc với \(\overrightarrow b \Leftrightarrow \overrightarrow a .\overrightarrow b = 0\)
+) Tích vô hướng của hai véc tơ \(\overrightarrow a \) và \(\overrightarrow b \) là: \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.c{\rm{os}}\left( {\overrightarrow a ,\overrightarrow b } \right)\)
\( \Rightarrow {\rm{cos}}\left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}}\)
Lời giải chi tiết:
+) Vì \(\left( {\overrightarrow a + 2\overrightarrow b } \right)\) vuông góc với \(\left( {5\overrightarrow a - 4\overrightarrow b } \right)\) nên:
\(\left( {\overrightarrow a + 2\overrightarrow b } \right).\left( {5\overrightarrow a - 4\overrightarrow b } \right) = 0 \Leftrightarrow 5{\overrightarrow a ^2} - 8{\overrightarrow b ^2} + 6\overrightarrow a .\overrightarrow b = 0 \Leftrightarrow \overrightarrow a .\overrightarrow b = \frac{{ - 5{{\overrightarrow a }^2} + 8{{\overrightarrow b }^2}}}{6}\)
Ta có: \(\left| {\overrightarrow a } \right| = \left| {\overrightarrow b } \right| \Leftrightarrow {\left| {\overrightarrow a } \right|^2} = {\left| {\overrightarrow b } \right|^2} \Rightarrow \overrightarrow a .\overrightarrow b = \frac{{3{{\overrightarrow a }^2}}}{6}\)
Vậy \({\rm{cos}}\left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}} = \frac{{\frac{{3{{\overrightarrow a }^2}}}{6}}}{{{{\overrightarrow a }^2}}} = \frac{1}{2}.\)
Chọn D.
Câu hỏi 37 :
Cho \(\Delta ABC\) có các đường trung tuyến \(AD,BE\) và \(CF.\) Tính \(\overrightarrow {AD} .\overrightarrow {BC} + \overrightarrow {BE} .\overrightarrow {CA} + \overrightarrow {CF} .\overrightarrow {AB} ?\)
- A \(1\)
- B \( - 1\)
- C \(0\)
- D \(\sqrt 2 \)
Đáp án: C
Phương pháp giải:
Sử dụng quy tắc ba điểm và trung tuyến vào từng tích vô hướng ở đề bài rồi lấy tổng tìm được ra kết quả.
Lời giải chi tiết:
Sử dụng các quy tắc ba điểm và trung tuyến, ta có:
\(\overrightarrow {AD} .\overrightarrow {BC} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\left( {\overrightarrow {AB} - \overrightarrow {AC} } \right) = \frac{1}{2}\left( {A{C^2} - A{B^2}} \right)\)
Tương tự ta có : \(\left\{ \begin{array}{l}\overrightarrow {BE} .\overrightarrow {CA} = \frac{1}{2}\left( {A{B^2} - B{C^2}} \right)\\\overrightarrow {CF} .\overrightarrow {AB} = \frac{1}{2}\left( {B{C^2} - A{C^2}} \right)\end{array} \right.\)
Vậy \(\overrightarrow {AD} .\overrightarrow {BC} + \overrightarrow {BE} .\overrightarrow {CA} + \overrightarrow {CF} .\overrightarrow {AB} = \frac{1}{2}\left( {A{C^2} - A{B^2}} \right) + \frac{1}{2}\left( {A{B^2} - B{C^2}} \right) + \frac{1}{2}\left( {B{C^2} - A{C^2}} \right) = 0.\)
Chọn C.
Câu hỏi 38 :
Tìm tập hợp các điểm \(M\) sao cho \(\overrightarrow {AM} .\overrightarrow {AB} = A{M^2}?\)
- A Đường tròn đường kính \(AC\)
- B Đường tròn đường kính \(BC\)
- C Đường tròn đường kính \(AC + BC\)
- D Đường tròn đường kính \(AB\)
Đáp án: D
Phương pháp giải:
Cho đoạn thẳng \(AB\); tập hợp các điểm \(M\) thỏa mãn:
+) \(\overrightarrow {AM} .\overrightarrow {AB} = 0\) là đường thẳng đi qua \(A\) và vuông góc với \(AB.\)
+) \(\overrightarrow {MA} .\overrightarrow {MB} = 0\) là đường tròn đường kính \(AB.\)
Lời giải chi tiết:
Ta có: \(\overrightarrow {AM} .\overrightarrow {AB} = A{M^2} \Leftrightarrow \overrightarrow {AM} .\overrightarrow {AB} - {\overrightarrow {AM} ^2} = 0 \Leftrightarrow \overrightarrow {AM} .\left( {\overrightarrow {AB} - \overrightarrow {AM} } \right) = 0 \Leftrightarrow \overrightarrow {AM} .\overrightarrow {MB} = 0 \Leftrightarrow \overrightarrow {MA} .\overrightarrow {MB} = 0\)
Vậy tập hợp điểm \(M\) là đường tròn đường kính \(AB.\)
Chọn D.
Câu hỏi 39 :
Trong mặt phẳng \(Oxy,\) cho hai điểm \(A\left( {2;2} \right),B\left( {5; - 2} \right).\) Tìm điểm \(M\)thuộc trục hoành sao cho \(\angle AMB = {90^0}?\)
- A \(M\left( { - 6;0} \right)\)
- B \(M\left( { - 2;0} \right)\)
- C \(M\left( {2;0} \right)\)
- D \(M\left( {6;0} \right)\)
Đáp án: D
Phương pháp giải:
+) \(\overrightarrow a \bot \overrightarrow b \Leftrightarrow \overrightarrow a .\overrightarrow b = 0.\)
+) Tích vô hướng của hai véc tơ \(\overrightarrow a \) và \(\overrightarrow b \) là: \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.c{\rm{os}}\left( {\overrightarrow a ,\overrightarrow b } \right)\)
Lời giải chi tiết:
+) Ta có: \(M \in Ox \Rightarrow M\left( {m;\,\,0} \right)\) và \(\left\{ {\begin{array}{*{20}{c}}{\overrightarrow {AM} = \left( {m - 2; - 2} \right)}\\{\overrightarrow {BM} = \left( {m - 5;\,\,2} \right)}\end{array}} \right.\)
Vì \(\angle AMB = {90^0} \Rightarrow \overrightarrow {AM} .\overrightarrow {BM} = 0 \Leftrightarrow \left( {m - 2} \right)\left( {m - 5} \right) + \left( { - 2} \right).2 = 0\)
\( \Leftrightarrow {m^2} - 7m + 6 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m = 1}\\{m = 6}\end{array} \Rightarrow \left[ {\begin{array}{*{20}{c}}{M\left( {1;0} \right)}\\{M\left( {6;0} \right)}\end{array}} \right.} \right..\)
Chọn D.
Câu hỏi 40 :
Trong mặt phẳng toạ độ \(Oxy,\)cho hai điểm \(A\left( {1;2} \right),B\left( { - 3;1} \right).\) Tìm toạ độ điểm \(C\) thuộc trục tung sao cho tam giác \(ABC\) vuông tại \(A.\)
- A \(C\left( {0;6} \right)\)
- B \(C\left( {5;0} \right)\)
- C \(C\left( {3;1} \right)\)
- D \(C\left( {0; - 6} \right)\)
Đáp án: A
Phương pháp giải:
Tích vô hướng của hai véc tơ \(\overrightarrow a \) và \(\overrightarrow b \) là: \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.c{\rm{os}}\left( {\overrightarrow a ,\overrightarrow b } \right)\)
Cho \(\overrightarrow a = \left( {{a_1};{a_2}} \right),\overrightarrow b = \left( {{b_1};{b_2}} \right).\) Khi đó: \(\overrightarrow a \bot \overrightarrow b \Leftrightarrow \overrightarrow a .\overrightarrow b = 0 \Leftrightarrow {a_1}{b_1} + {a_2}{b_2} = 0.\)
Lời giải chi tiết:
Ta có \(C \in Oy\) nên \(C\left( {0;c} \right)\) và \(\left\{ {\begin{array}{*{20}{c}}{\overrightarrow {AB} = \left( { - 4; - 1} \right)}\\{\overrightarrow {AC} = \left( { - 1;\,\,c - 2} \right)}\end{array}} \right.\)
Tam giác \(ABC\) vuông tại \(A\) nên \(\overrightarrow {AB} .\overrightarrow {AC} = 0 \Leftrightarrow \left( { - 4} \right).\left( { - 1} \right) + \left( { - 1} \right).\left( {c - 2} \right) = 0 \Leftrightarrow c - 2 = 4 \Leftrightarrow c = 6\)
\( \Rightarrow C\left( {0;6} \right)\)
Chọn A.
>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10
 |
 |
 |
 |
 |
 |
 |
 |
Các bài khác cùng chuyên mục




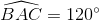 thì:
thì: