40 bài tập trắc nghiệm hệ thức lượng trong tam giác mức độ vận dụng, vận dụng cao
Làm đề thiCâu hỏi 1 :
Tam giác ABC vuông cân tại A có AB = 2a. Đường trung tuyến BM có độ dài là:
- A \(3a\)
- B \(2a\sqrt 2 \)
- C \(2a\sqrt 3 \)
- D \(a\sqrt 5 \)
Đáp án: D
Phương pháp giải:
+ Sử dụng tính chất tam giác cân có AB = AC = 2a.
+ Sử dụng định lý Pitago \(B{C^2} = A{B^2} + A{C^2}\) để tính BC.
+ Sử dụng công thức trung tuyến \(MB_{}^2 = {{B{C^2} + A{B^2}} \over 2} - {{A{C^2}} \over 4}\).
Lời giải chi tiết:
+ Ta có AB = AC = 2a.
+ Ta có \(BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {4{a^2} + 4{a^2}} = 2\sqrt 2 a\).
+ \(MB_{}^2 = {{B{C^2} + A{B^2}} \over 2} - {{A{C^2}} \over 4} = {{8{a^2} + 4{a^2}} \over 2} - {{4{a^2}} \over 4} = 5{a^2} \Rightarrow MB = a\sqrt 5 \).
Chọn D.
Câu hỏi 2 :
Tam giác ABC có BC = 10 và \(\widehat A = {30^0}\). Khi đó, bán kính đường tròn ngoại tiếp tam giác ABC là:
- A 5
- B 10
- C \({{10} \over {\sqrt 3 }}\)
- D \(10\sqrt 3 \)
Đáp án: B
Phương pháp giải:
Sử dụng công thức định lí sin: \({{BC} \over {\sin A}} = 2R\)
Lời giải chi tiết:
Từ \({{BC} \over {\sin A}} = 2R \Rightarrow R = {{BC} \over {2\sin A}} = {{10} \over {2\sin {{30}^0}}} = 10\)
Chọn B.
Câu hỏi 3 :
Tìm bán kính đường tròn ngoại tiếp tam giác \(ABC\) biết \(b = 7cm,\,\,c = 5cm,\,\,{\mathop{\rm cosA}\nolimits} = {3 \over 5}\).
- A \(R = {{5\sqrt 2 } \over 2}\)
- B \(R = {5 \over 2}\)
- C \(R = {{\sqrt 2 } \over 2}\)
- D \(R = {{2\sqrt 2 } \over 5}\)
Đáp án: A
Phương pháp giải:
Vận dụng công thức \({a \over {\sin A}} = {b \over {\sin B}} = {c \over {\sin C}} = 2R\)
Lời giải chi tiết:
Theo định lí cosin ta có \({a^2} = {b^2} + {c^2} - 2bc\cos A = {7^2} + {5^2} - 2.7.5.{3 \over 5} = 32 \Rightarrow a = 4\sqrt 2 \)
Từ công thức \({\sin ^2}A + {\cos ^2}A = 1 \Rightarrow {\mathop{\rm sinA}\nolimits} = {4 \over 5}\)
Theo định lí sin ta có \({a \over {\sin A}} = 2R \Rightarrow R = {a \over {2\sin A}} = {{4\sqrt 2 } \over {2.{4 \over 5}}} = {{5\sqrt 2 } \over 2}\).
Chọn A.
Câu hỏi 4 :
Nếu tam giác ABC có \({a^2} < {b^2} + {c^2}\) thì:
- A góc A nhọn
- B góc A tù
- C góc A vuông
- D góc A là góc nhỏ nhất
Đáp án: A
Phương pháp giải:
Sử dụng công thức định lí cosin \({a^2} = {b^2} + {c^2} - 2bc\cos A\).
Lời giải chi tiết:
Ta có \(\cos A = {{{b^2} + {c^2} - {a^2}} \over {2bc}}\).
Theo giả thiết \({a^2} < {b^2} + {c^2} \Rightarrow \cos A > 0\).
Vậy góc A nhọn.
Chọn A.
Câu hỏi 5 :
Cho tam giác ABC có AB = 4cm, BC = 7cm, CA = 9cm. Giá trị cosA là:
- A \({2 \over 3}\)
- B \({1 \over 3}\)
- C \({-2 \over 3}\)
- D \({1 \over 2}\)
Đáp án: A
Phương pháp giải:
Sử dụng công thức định lí cosin \({a^2} = {b^2} + {c^2} - 2bc\cos A\).
Lời giải chi tiết:
Ta có \(\cos A = {{{b^2} + {c^2} - {a^2}} \over {2bc}} ={{{9^2} + {4^2} - {7^2}} \over {2.9.4}}={2 \over 3}\).
Chọn A.
Câu hỏi 6 :
Trong tam giác ABC, hệ thức nào sau đây đúng?
- A \({{\tan A} \over {\tan B}} = {{{c^2} + {a^2} - {b^2}} \over {{c^2} + {b^2} - {a^2}}}\)
- B \({{\cot A} \over {\cot B}} = {{{c^2} + {a^2} - {b^2}} \over {{c^2} + {b^2} - {a^2}}}\)
- C \({{\tan A} \over {\tan B}} = {{{c^2} + {b^2} - {a^2}} \over {{c^2} + {a^2} - {b^2}}}\)
- D \({{\tan A} \over {\tan B}} = {{{c^2} + {b^2} + 2a} \over {{c^2} + {a^2} + 2b}}\)
Đáp án: A
Phương pháp giải:
Áp dụng định lí cosin: \(\eqalign{ & {a^2} = {b^2} + {c^2} - 2bc\,CosA \cr & {b^2} = {a^2} + {c^2} - 2ac\,CosB \cr} \) và định lý sin: \({a \over {\sin \,A}} = {b \over {\sin \,B}} = 2R\)
Lời giải chi tiết:
Áp dụng định lí cosin:
\(\eqalign{ & {a^2} = {b^2} + {c^2} - 2bc\,cosA \Rightarrow \cos A = {{{c^2} + {b^2} - {a^2}} \over {2bc}} \cr & {b^2} = {a^2} + {c^2} - 2ac\,cosB \Rightarrow \cos B = {{{c^2} + {a^2} - {b^2}} \over {2ac}} \cr} \).
và định lý sin: \({a \over {\sin \,A}} = {b \over {\sin \,B}} = 2R \Rightarrow \sin A = {a \over {2R}},\sin B = {b \over {2R}}.\)
\({{\tan A} \over {\tan B}} = {{\sin A} \over {\cos A}}.{{\cos B} \over {\sin B}} = {{{a \over {2R}}} \over {{{{c^2} + {b^2} - {a^2}} \over {2bc}}}}.{{{{{c^2} + {a^2} - {b^2}} \over {2ac}}} \over {{b \over {2R}}}} = {{{c^2} + {a^2} - {b^2}} \over {{c^2} + {b^2} - {a^2}}}\).
Chọn A.
Câu hỏi 7 :
Cho tam giác ABC có \({1 \over {b + a}} + {1 \over {a + c}} = {3 \over {a + b + c}}\). Nhận xét nào sau đây đúng.
- A Tam giác ABC có \(\widehat {BAC} = {60^0}\)
- B Tam giác ABC đều
- C Tam giác ABC vuông cân tại A
- D Tam giác ABC có \(\widehat {BAC} = {120^0 }\)
Đáp án: A
Phương pháp giải:
Sử dụng phương pháp biến đổi tương đương kết hợp sử dụng công thức định lí cosin: \({a^2} = {b^2} + {c^2} - 2bc.cosA\)
Lời giải chi tiết:
\(\eqalign{ & {1 \over {b + a}} + {1 \over {a + c}} = {3 \over {a + b + c}} \Leftrightarrow {{a + b + c} \over {b + a}} + {{a + b + c} \over {a + c}} = 3 \Leftrightarrow 1 + {c \over {b + a}} + 1 + {b \over {a + c}} = 3 \cr & \Leftrightarrow {c \over {b + a}} + {b \over {a + c}} = 1 \Leftrightarrow c(a + c) + b(a + b) = (b + a)(a + c) \Leftrightarrow ca + {c^2} + ab + {b^2} = ab + bc + {a^2} + ac \cr & \Leftrightarrow {c^2} + {b^2} - {a^2} = bc \Leftrightarrow 2bc.\cos A = bc \Leftrightarrow \cos A = {1 \over 2} \Leftrightarrow \widehat A = {60^0}. \cr} \).
Chọn A.
Câu hỏi 8 :
Tam giác ABC có ba cạnh là 6, 8, 10. Khi đó, bán kính đường tròn nội tiếp tam giác ABC là:
- A \(\sqrt 3 \)
- B 4
- C 2
- D 1
Đáp án: C
Phương pháp giải:
+ Tính\(p = {{a + b + c} \over 2}\).
+ Sử dụng công thức \(S = \sqrt {p(p - a)(p - b)(p - c)} \).
+ Sử dụng công thức \(S = p.r\).
Lời giải chi tiết:
+ Ta có \(p = {{6 + 8 + 10} \over 2} = 12\)
+ \(S = \sqrt {p(p - a)(p - b)(p - c)} =\sqrt {12.6.4.2} = 24\)
+ \(r = {S \over p} = {{24} \over {12}} = 2\)
Chọn C.
Câu hỏi 9 :
Cho tam giác ABC có AB = 8cm, AC = 18cm và có diện tích bằng \(64c{m^2}\). Giá trị sinA là:
- A \({{\sqrt 3 } \over 2}\)
- B \({3 \over 8}\)
- C \({4 \over 5}\)
- D \({8 \over 9}\)
Đáp án: D
Phương pháp giải:
Sử dụng công thức: \(S = {1 \over 2}AB.CA.\sin A\).
Lời giải chi tiết:
Ta có \(S = {1 \over 2}AB.AC.\sin A \Rightarrow \sin A = {{2S} \over {AB.AC}} = {{2.64} \over {8.18}} = {8 \over 9}\)
Chọn D.
Câu hỏi 10 :
Cho tam giác ABC thỏa mãn hệ thức \(m_a^2 = m_b^2 + m_c^2\). Khi đó, ta có hệ thức nào sau đây?
- A \({a^2} = S.\cot A\)
- B \({a^2} = 2S.\cot A\)
- C \({a^2} = 3S.\cot A\)
- D \({a^2} = 4S.\cot A\)
Đáp án: A
Phương pháp giải:
Sử dụng công thức trung tuyến: \(\eqalign{ & m_a^2 = {{{b^2} + {c^2}} \over 2} - {{{a^2}} \over 4} \cr & m_b^2 = {{{a^2} + {c^2}} \over 2} - {{{b^2}} \over 4} \cr & m_c^2 = {{{a^2} + {b^2}} \over 2} - {{{c^2}} \over 4} \cr} \), công thức định lí cosin: \({a^2} = {b^2} + {c^2} - 2bc\,cosA\) và công thức tính diện tích \(S = {1 \over 2}bc\sin A\).
Lời giải chi tiết:
\(\eqalign{ & \left\{ \matrix{ {a^2} = {b^2} + {c^2} - 2bc\,cosA \Rightarrow {b^2} + {c^2} - {a^2} = 2bc.\cos A \hfill \cr S = {1 \over 2}bc\sin A \Rightarrow bc = {{2S} \over {\sin A}} \hfill \cr} \right. \cr & m_a^2 = m_b^2 + m_c^2 \Leftrightarrow {{{b^2} + {c^2}} \over 2} - {{{a^2}} \over 4} = {{{a^2} + {c^2}} \over 2} - {{{b^2}} \over 4} + {{{a^2} + {b^2}} \over 2} - {{{c^2}} \over 4} \cr & \Leftrightarrow 2{b^2} + 2{c^2} - {a^2} = 2{a^2} + 2{c^2} - {b^2} + 2{a^2} + 2{b^2} - {c^2} \Leftrightarrow {b^2} + {c^2} = 5{a^2} \cr & \Leftrightarrow {b^2} + {c^2} - {a^2} = 4{a^2} \Leftrightarrow 2bc\cos A = 4{a^2} \Leftrightarrow {a^2} = {{bc\cos A} \over 2} \cr & \Leftrightarrow {a^2} = {{S.\cos A} \over {\sin A}} \Leftrightarrow {a^2} = S.\cot A \cr} \).
Chọn A.
Câu hỏi 11 :
Cho tam giác ABC không cân và thỏa mãn điều kiện \({b \over c} = {{{m_c}} \over {{m_b}}}\). Khi đó, ta có hệ thức nào dưới đây đúng?
- A \({b^2} + {c^2} = {a^2}\)
- B
\({b^2} + {c^2} = 2{a^2}\)
- C \({b^2} + {c^2} = 3{a^2}\)
- D \({b^2} + {c^2} = 4{a^2}\)
Đáp án: B
Phương pháp giải:
Sử dụng công thức trung tuyến\(\left\{ \matrix{ m_b^2 = {{{a^2} + {c^2}} \over 2} - {{{b^2}} \over 4} \hfill \cr m_c^2 = {{{a^2} + {b^2}} \over 2} - {{{c^2}} \over 4} \hfill \cr} \right.\) và biến đổi tương đương.
Lời giải chi tiết:
Từ giả thiết \({b \over c} = {{{m_c}} \over {{m_b}}}\) ta có
\({{{b^2}} \over {{c^2}}} = {{m_c^2} \over {m_b^2}} = {{{{{a^2} + {b^2}} \over 2} - {{{c^2}} \over 4}} \over {{{{a^2} + {c^2}} \over 2} - {{{b^2}} \over 4}}} = {{2{a^2} + 2{b^2} - {c^2}} \over {2{a^2} + 2{c^2} - {b^2}}}\)
Suy ra \(2{a^2}{b^2} + 2{b^2}{c^2} - {b^4} = 2{a^2}{c^2} + 2{b^2}{c^2} - {c^4} \Leftrightarrow 2{a^2}({b^2} - {c^2}) = {b^4} - {c^4} = \left( {{b^2} - {c^2}} \right)\left( {{b^2} + {c^2}} \right)\).
Do tam giác không cân nên ta có \(b \ne c\) . Suy ra \(2{a^2} = {b^2} + {c^2}\).
Chọn B.
Câu hỏi 12 :
Tam giác ABC đều cạnh 2a, ngoại tiếp đường tròn bán kính r. Khi đó, bán kính của đường tròn nội tiếp tam giác ABC là
- A \({{a\sqrt 3 } \over 2}\)
- B \({{2a\sqrt 2 } \over 5}\)
- C \({{a\sqrt 3 } \over 3}\)
- D \({{2a\sqrt 3 } \over 7}\)
Đáp án: C
Phương pháp giải:
Sử dụng các công thức tính diện tích tam giác \(S = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} \) và \(S = pr\)
Lời giải chi tiết:
+ Ta có \(p = {{2a + 2a + 2a} \over 2} = 3a\)
+ Có \(S = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} = \sqrt {3a.a.a.a} = \sqrt 3 {a^2}\)
+ \(S = p.r \Rightarrow r = {S \over p} = {{\sqrt 3 a} \over 3}\)
Chọn C
Câu hỏi 13 :
Cho \(\Delta ABC\) thỏa mãn hệ thức\({{{b^2} - {a^2}} \over {2c}} = b\cos A - a\cos B\). Khẳng định nào sau đây đúng?
- A \(\Delta ABC\) cân tại C.
- B \(\Delta ABC\) vuông tại C
- C \(\Delta ABC\) có \(\widehat C = {60^0}\)
- D \(\Delta ABC\) có \(\widehat C = {30^0}\)
Đáp án: A
Phương pháp giải:
Áp dụng định lý cosin cho \(\Delta ABC\):
\(\eqalign{ & \,\,\,{a^2} = {b^2} + {c^2} - 2bc\cos A \cr & \,\,\,{b^2} = {a^2} + {c^2} - 2ac\cos B \cr} \).
Lời giải chi tiết:
Ta có: \({{{b^2} - {a^2}} \over {2c}} = b\cos \,A - a\,cos\,B \Leftrightarrow {b^2} - {a^2} = 2bc\cos A - 2ac\cos B\,\,\,\left( * \right)\).
Áp dụng định lý cosin cho \(\Delta ABC\):
\(\eqalign{ & \,\,\,\,\,{a^2} = {b^2} + {c^2} - 2bc\cos A \cr & \Rightarrow 2bc\cos A = {b^2} + {c^2} - {a^2} \cr} \).
Tương tự: \(2ac\cos B = {a^2} + {c^2} - {b^2}\).
\(\eqalign{ & \left( * \right) \Leftrightarrow {b^2} - {a^2} = \left( {{b^2} + {c^2} - {a^2}} \right) - \left( {{a^2} + {c^2} - {b^2}} \right) \cr & \,\,\,\,\,\,\, \Leftrightarrow {b^2} - {a^2} = {b^2} + {c^2} - {a^2} - {a^2} - {c^2} + {b^2} \cr & \,\,\,\,\,\,\, \Leftrightarrow {b^2} - {a^2} = 2{b^2} - 2{a^2} \cr & \,\,\,\,\,\,\, \Leftrightarrow {a^2} = {b^2} \Leftrightarrow a = b \cr} \)
\( \Rightarrow \Delta ABC\) cân tại \(C\).
Chọn A
Câu hỏi 14 :
Cho \(\Delta ABC\) có hai trung tuyến \(BM,\,\,CN\) vuông góc với nhau. Khi đó, hệ thức nào sau đây đúng.
- A \({b^2} + {c^2} = 2{a^2}\).
- B \({b^2} + {c^2} = 3{a^2}\)
- C \({b^2} + {c^2} = 4{a^2}\)
- D \({b^2} + {c^2} = 5{a^2}\)
Đáp án: D
Phương pháp giải:
Sử dụng công thức trung tuyến \(\eqalign{ & m_b^2 = {{{a^2} + {c^2}} \over 2} - {{{b^2}} \over 4} \cr & m_c^2 = {{{a^2} + {b^2}} \over 2} - {{{c^2}} \over 4} \cr} \), tính chất của trọng tâm và công thức định lý Pitago.
Lời giải chi tiết:
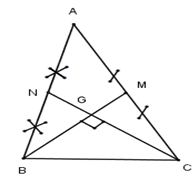
Ta có:
\(\eqalign{ & m_b^2 = {{{a^2} + {c^2}} \over 2} - {{{b^2}} \over 4} \cr & m_c^2 = {{{a^2} + {b^2}} \over 2} - {{{c^2}} \over 4} \cr} \)
\(BM \cap CN = \left\{ G \right\} \Rightarrow \) G là trọng tâm \(\Delta ABC \Rightarrow BG = {2 \over 3}{m_b};\,\,\,CG = {2 \over 3}{m_c}\)
\(BM \bot CN \Leftrightarrow \Delta BGC\) vuông tại G.
\(\eqalign{ & \Leftrightarrow B{G^2} + C{G^2} = B{C^2} \cr & \Leftrightarrow {\left( {{2 \over 3}{m_b}} \right)^2} + {\left( {{2 \over 3}{m_c}} \right)^2} = {a^2} \cr & \Leftrightarrow {4 \over 9}\left( {{{{a^2} + {c^2}} \over 2} - {{{b^2}} \over 4}} \right) + {4 \over 9}\left( {{{{a^2} + {b^2}} \over 2} - {{{c^2}} \over 4}} \right) = {a^2} \cr & \Leftrightarrow 2\left( {{a^2} + {c^2}} \right) - {b^2} + 2\left( {{a^2} + {b^2}} \right) - {c^2} = 9{a^2} \cr & \Leftrightarrow 2{a^2} + 2{c^2} - {b^2} + 2{a^2} + 2{b^2} - {c^2} = 9{a^2} \cr & \Leftrightarrow {b^2} + {c^2} = 5{a^2} \cr} \)
Chọn D
Câu hỏi 15 :
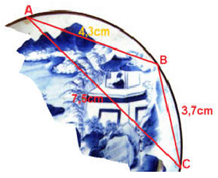
Trong khi khai quật một ngôi mộ cổ, các nhà khảo cổ học đã tìm được một chiếc đĩa cổ hình tròn bị vỡ, các nhà khảo cổ muốn khôi phục lại hình dạng chiếc đĩa này. Để xác định bán kính của chiếc đĩa, các nhà khảo cổ lấy 3 điểm trên chiếc đĩa và tiến hành đo đạc thu được kết quả như hình vẽ (\(AB = 4,3cm;\,\,BC = 3,7cm;\,\,CA = 7,5cm\)). Bán kính của chiếc đĩa này bằng (kết quả làm tròn tới hai chữ số sau dấu phẩy)
- A \(5,73cm\)
- B \(6,01cm\)
- C \(5,85cm\)
- D \(4,57cm\)
Đáp án: A
Phương pháp giải:
Cho tam giác có 3 cạnh lần lượt là \(a,b,c,\) nửa chu vi \(p = \frac{{a + b + c}}{2}.\) Khi đó
\(S = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} = \frac{{abc}}{{4R}}\) (\(R\) là bán kính đường tròn ngoại tiếp tam giác)
Lời giải chi tiết:
Dễ thấy bán kính của chiếc đĩa là bán kính đường tròn ngoại tiếp tam giác ABC
Tam giác ABC có nửa chu vi \(p = \frac{{4,3 + 3,7 + 7,5}}{2} = 7,75\)
\(\begin{array}{l}S = \frac{{abc}}{{4R}} \Rightarrow R = \frac{{abc}}{{4S}} = \frac{{abc}}{{4\sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} }}\\ = \frac{{4,3.3,7.7,5}}{{4\sqrt {7,75\left( {7,75 - 4,3} \right)\left( {7,75 - 3,7} \right)\left( {7,75 - 7,5} \right)} }} \approx 5,73cm.\end{array}\)
Chọn A.
Câu hỏi 16 :
Hai chiếc tàu thuỷ cùng xuất phát từ Cảng A, đi thẳng theo hai hướng tạo với nhau một góc 600. Tàu thứ nhất chạy với tốc độ 30km/h, tàu thứ hai chạy với tốc độ 40km/h. Hỏi sau 2 giờ hai tàu cách nhau bao nhiêu km?
- A \(70km\)
- B \(10\sqrt {13} \,\,km\)
- C \(20\sqrt {13} \,\,km\)
- D \(20\sqrt 3 \,\,km\)
Đáp án: C
Phương pháp giải:
Áp dụng định lý cosin : Cho tam giác ABC ta có \({a^2} = {b^2} + {c^2} - 2bc.\cos \angle A\)
Lời giải chi tiết:
Sau 2 giờ tàu thứ nhất đi được \(AB = 30.2 = 60\)(km)
Sau 2 giờ tàu thứ hai đi được \(AC = 40.2 = 80\) (km)
Sau 2 giờ khoảng cách giữa hai tàu là
\(BC = \sqrt {A{B^2} + A{C^2} - 2AB.AC.\cos \angle A} = \sqrt {{{60}^2} + {{80}^2} - 2.60.80.\cos {{60}^o}} = 20\sqrt {13} \,\,\left( {km} \right)\)
Chọn C.
Câu hỏi 17 :
Cho tam giác ABC có \(AC = 7cm,\,\,BC = 10cm\) và \(\widehat {BAC} = {60^0}\). Tính \(\sin \widehat {ABC}\) và tính độ dài cạnh AB (yêu cầu tính ra kết quả chính xác, không tính xấp xỉ).
- A \(AB=\frac{1+\sqrt{253}}{2}\)
- B \(AB=\frac{7+\sqrt{253}}{2}\)
- C \(AB=\frac{7+\sqrt{253}}{5}\)
- D \(AB=\frac{7+\sqrt{253}}{7}\)
Đáp án: B
Phương pháp giải:
+) Áp dụng định lí sin để tính sin góc ABC.
+) Áp dụng định lí cosin để tính AB.
Lời giải chi tiết:
Áp dụng định lí sin ta có: \(\frac{{AC}}{{\sin \widehat {ABC}}} = \frac{{BC}}{{\sin \widehat {BAC}}} \Leftrightarrow \frac{7}{{\sin \widehat {ABC}}} = \frac{{10}}{{\sin {{60}^0}}} \Leftrightarrow \sin \widehat {ABC} = \frac{{7.\sin {{60}^0}}}{{10}} = \frac{{7\sqrt 3 }}{{20}}\)
Áp dụng định lí cosin ta có:
\(\begin{array}{l}\,\,\,\,\,\,\cos \widehat {BAC} = \frac{{A{B^2} + A{C^2} - B{C^2}}}{{2AB.AC}} \Leftrightarrow \cos {60^0} = \frac{{A{B^2} + {7^2} - {{10}^2}}}{{2.AB.7}}\\ \Leftrightarrow 7AB = A{B^2} - 51 \Leftrightarrow A{B^2} - 7AB - 51 = 0\\ \Leftrightarrow \left[ \begin{array}{l}AB = \frac{{7 + \sqrt {253} }}{2}\\AB = \frac{{7 - \sqrt {253} }}{2} < 0\,\,\left( {ktm} \right)\end{array} \right. \Rightarrow AB = \frac{{7 + \sqrt {253} }}{2}\end{array}\)
Câu hỏi 18 :
Cho tam giác ABC có \(a = 4\),\(\angle B=75^0\),\(\angle C=60^0\). Bán kính đường tròn ngoại tiếp tam giác ABC là:
- A \(2\sqrt 2 \).
- B \(2\sqrt 6 \).
- C \(\frac{{4\sqrt 3 }}{3}\).
- D \(4\).
Đáp án: A
Phương pháp giải:
Tổng 3 góc trong một tam giác bằng \({180^o}\)
Áp dụng định lý sin để tính.
Lời giải chi tiết:
Xét tam giác ABC ta có: \(\angle A + \angle B + \angle C = {180^o} \Rightarrow \angle A = {180^o} - \angle B - \angle C = {45^o}\)
Theo định lý sin ta có: \(\frac{a}{{\sin \angle A}} = 2R \Rightarrow R = \frac{a}{{2\sin \angle A}} = \frac{4}{{2.\sin {{45}^o}}} = 2\sqrt 2 \)
Chọn A.
Câu hỏi 19 :
Cho tam giác ABC vuông cân tại A và \(AB = 2.\) M là trung điểm AB. Khi đó \(\tan \angle MCB\) bằng:
- A \(\frac{1}{2}\).
- B \(\frac{1}{3}\).
- C \(\frac{1}{5}\).
- D \(\tan {22^0}30'\).
Đáp án: B
Phương pháp giải:
\(\tan \angle ACB = \frac{{\tan \angle MCA + \tan \angle MCB}}{{1 - \tan \angle MCA.\tan \angle MCB}}\)
Lời giải chi tiết:
Ta có tam giác ABC vuông cân tại A và AB = 2, M là trung điểm AB
\(\begin{array}{l} \Rightarrow MA = \frac{1}{2}AB = 1\,\,;\,\,AC = AB = 2\\ \Rightarrow \tan \angle ACB = \frac{{AB}}{{AC}} = 1\,\,\,;\,\,\,\tan \angle MCA = \frac{{AM}}{{AC}} = \frac{1}{2}\end{array}\)
Mặt khác \(\tan \angle ACB = \frac{{\tan \angle MCA + \tan \angle MCB}}{{1 - \tan \angle MCA.\tan \angle MCB}}\)
Hay \(1 = \frac{{\frac{1}{2} + \tan \angle MCB}}{{1 - \frac{1}{2}.\tan \angle MCB}} \Leftrightarrow 1 - \frac{1}{2}\tan \angle MCB = \frac{1}{2} + \tan \angle MCB\)
\( \Leftrightarrow \frac{3}{2}\tan \angle MCB = \frac{1}{2} \Leftrightarrow \tan \angle MCB = \frac{1}{3}\)
Chọn B.
Câu hỏi 20 :
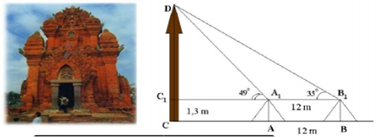
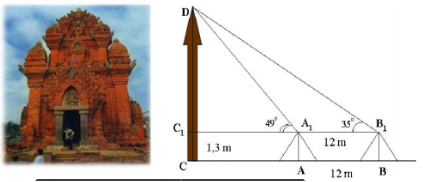
Muốn đo chiều cao của tháp chàm Por Klong Garai ở Ninh Thuận, người ta lấy hai điểm \(A\) và \(B\) trên mặt đất có khoảng cách \(AB = 12m\) cùng thẳng hàng với chân \(C\) của tháp để đặt hai giác kế. Chân của giác kế có chiều cao \(h = 1,3m.\) Gọi \(D\) là đỉnh tháp và hai điểm \({A_1},{B_1}\) cùng thẳng hàng với \({C_1}\) thuộc chiều cao \(CD\) của tháp. Người ta đo được góc \(\angle D{A_1}{C_1} = {49^o}\) và \(\angle D{B_1}{C_1} = {35^o}.\)Tính chiều cao \(CD\) của tháp.
- A \(20,47m\)
- B \(21,47m\)
- C \(21,77m\)
- D \(22,77m\)
Đáp án: D
Phương pháp giải:
Ở bài toán này, ta sử dụng định lí hàm sin vào tam giác \({A_1}D{B_1}\) để tính \({A_1}D\)và vào tam giác \({C_1}{A_1}D\) để tính \({C_1}D\) Khi đó chiều cao của tháp là \(CD = {C_1}D + C{C_1}\)
Lời giải chi tiết:
Ta có \(\angle {C_1}D{A_1} = {90^o} - {49^o} = {41^o};\,\,\,\angle {C_1}D{B_1} = {90^o} - {35^o} = {55^o},\) nên \(\angle {A_1}D{B_1} = {14^o}.\)
Xét \(\Delta {A_1}D{B_1}:\) \(\frac{{{A_1}{B_1}}}{{\sin \angle {A_1}D{B_1}}} = \frac{{{A_1}D}}{{\sin \angle {A_1}{B_1}D}} \Rightarrow {A_1}D = \frac{{12.\sin {{35}^o}}}{{\sin {{14}^o}}} \approx 28,45m.\)
Xét \(\Delta {C_1}{A_1}D\) vuông tại \({C_1}:\) \(\sin \angle {C_1}{A_1}D = \frac{{{C_1}D}}{{{A_1}D}} \Rightarrow {C_1}D = {A_1}D.\sin \angle {C_1}{A_1}D = 28,45.\sin {49^o} \approx 21,47m\)
\( \Rightarrow CD = {C_1}D + C{C_1} \approx 22,77m\)
Chọn D.
Câu hỏi 21 :
Tam giác \(ABC\) có \(BC = a,CA = b.\) Tam giác \(ABC\) có diện tích lớn nhất khi góc \(C\) bằng bao nhiêu?
- A \({60^o}\)
- B \({90^o}\)
- C \({150^o}\)
- D \({120^o}\)
Đáp án: B
Phương pháp giải:
Ta sử dụng công thức tính diện tích tam giác: \(S = \frac{1}{2}ab\sin C = \frac{1}{2}bc\sin A = \frac{1}{2}ac\sin B\)
Lời giải chi tiết:
Diện tích tam giác \(ABC\) là \({S_{\Delta ABC}} = \frac{1}{2}.AC.BC.\sin \angle ACB = \frac{1}{2}ab\sin \angle ACB\)
Vì \(a,b\) không đổi và \(\sin \angle ACB \le 1,\,\,\forall C\) nên \({S_{\Delta ABC}} \le \frac{{ab}}{2}\)
Dấu “\( = \)” xảy ra khi và chỉ khi \(\sin \angle ACB = 1 \Leftrightarrow \angle ACB = {90^o}.\)
Chọn B
Câu hỏi 22 :
Tam giác \(ABC\) vuông cân tại \(A\) và nội tiếp trong đường tròn tâm \(O\) bán kính \(R.\) Gọi \(r\) là bán kính đường tròn nội tiếp tam giác \(ABC.\) Khi đó tỉ số \(\frac{R}{r}\) bằng:
- A \(1 + \sqrt 2 \)
- B \(\frac{{2 + \sqrt 2 }}{2}\)
- C \(\frac{{\sqrt 2 - 1}}{2}\)
- D \(\frac{{1 + \sqrt 2 }}{2}\)
Đáp án: A
Phương pháp giải:
Ta sử dụng công thức tính diện tích tam giác :
\(\begin{array}{l}S = \frac{{abc}}{{4R}}\\S = pr\end{array}\) , trong đó: \(R:\) bán kính đường tròn ngoại tiếp tam giác; \(r:\) bán kính đường tròn nội tiếp tam giác.
Lời giải chi tiết:
Ta có: \(R = \frac{{abc}}{{4S}},r = \frac{S}{p}\)
Vì tam giác \(ABC\) vuông cân tại \(A\) nên \(b = c\) và \(a = \sqrt {{b^2} + {c^2}} = b\sqrt 2 \)
Khi đó: \(\frac{R}{r} = \frac{{abc.p}}{{4{S^2}}} = \frac{{abc.\frac{{a + b + c}}{2}}}{{4.\frac{1}{4}.{{\left( {b.c} \right)}^2}}} = \frac{{a\left( {a + 2b} \right)}}{{2{b^2}}} = \frac{{2{b^2}\left( {1 + \sqrt 2 } \right)}}{{2{b^2}}} = 1 + \sqrt 2 \)
Chọn A
Câu hỏi 23 :
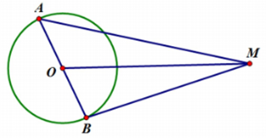
Cho đường tròn tâm \(O\) bán kính \(R\) và điểm \(M\) thoả mãn \(MO = 3R.\) Một đường kính \(AB\) thay đổi trên đường tròn. Giá trị nhỏ nhất của biểu thức \(S = MA + MB.\)
- A \(\min S = 6R\)
- B \(\min S = 4R\)
- C \(\min S = 2R\)
- D \(\min S = R\)
Đáp án: A
Phương pháp giải:
B1: Ta tính \(MA,MB\) dựa vào định lí hàm cosin trong hai tam giác \(\Delta MOA,\Delta MOB.\)
B2: Đánh giá \(S = MA + MB \ge c\left( {c = const} \right) \Rightarrow \min S = c\)
Lời giải chi tiết:
Gọi \(\angle MOA = \alpha \Rightarrow \angle MOB = {180^o} - \alpha \)
Ta có: \(\begin{array}{l}MA = \sqrt {M{O^2} + O{A^2} - 2.MO.OA.cos\alpha } = \sqrt {9{R^2} + {R^2} - 6{R^2}\cos \alpha } = R\sqrt {10 - 6\cos \alpha } .\\MB = \sqrt {M{O^2} + O{B^2} - 2.MO.OB.cos\left( {{{180}^o} - \alpha } \right)} = \sqrt {9{R^2} + {R^2} + 6{R^2}.cos\alpha } = R\sqrt {10 + 6\cos \alpha } \end{array}\)
Khi đó :
\(\begin{array}{l}S = \sqrt {10 - 6\cos \alpha } + \sqrt {10 + 6\cos \alpha } \\ \Rightarrow {S^2} = 20 + 2\sqrt {100 - 36{{\cos }^2}\alpha } \ge 20 + 2\sqrt {100 - 36} = 36\\ \Rightarrow S \ge 6.\end{array}\)
Dấu “\( = \)” xảy ra \( \Leftrightarrow {\cos ^2}\alpha = 1 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\cos \alpha = 1}\\{\cos \alpha = - 1}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\alpha = {0^o}}\\{\alpha = {{180}^o}}\end{array}} \right.} \right.\)
Ta có: \(S = MA + MB \ge 6 \Rightarrow \min S = 6R \Leftrightarrow A,O,B,M\) thẳng hàng.
Chọn A
Câu hỏi 24 :
Tam giác \(ABC\) có ba đường trung tuyến \({m_a},{m_b},{m_c}\) thoả mãn \(5{m_a}^2 = {m_b}^2 + {m_c}^2.\) Khi đó tam giác là tam giác gì?
- A Tam giác cân.
- B Tam giác đều.
- C Tam giác vuông.
- D Tam giác vuông cân.
Đáp án: C
Phương pháp giải:
Áp dụng định lí đường trung tuyến của tam giác \(ABC\):
\(\begin{array}{l}{m_a}^2 = \frac{{2\left( {{b^2} + {c^2}} \right) - {a^2}}}{4}\\{m_b}^2 = \frac{{2\left( {{a^2} + {c^2}} \right) - {b^2}}}{4}\\{m_c}^2 = \frac{{2\left( {{a^2} + {b^2}} \right) - {c^2}}}{4}\end{array}\)
Lời giải chi tiết:
Ta có: \(\left\{ \begin{array}{l}{m_a}^2 = \frac{{2\left( {{b^2} + {c^2}} \right) - {a^2}}}{4}\\{m_b}^2 = \frac{{2\left( {{a^2} + {c^2}} \right) - {b^2}}}{4}\\{m_c}^2 = \frac{{2\left( {{a^2} + {b^2}} \right) - {c^2}}}{4}\end{array} \right.\) mà \(5{m_a}^2 = {m_b}^2 + {m_c}^2\)
\(\begin{array}{l} \Rightarrow 5\left( {\frac{{{b^2} + {c^2}}}{2} - \frac{{{a^2}}}{4}} \right) = \frac{{{a^2} + {c^2}}}{2} - \frac{{{b^2}}}{4} + \frac{{{a^2} + {b^2}}}{2} - \frac{{{c^2}}}{4}\\ \Leftrightarrow 10{b^2} + 10{c^2} - 5{a^2} = 2{a^2} + 2{c^2} - {b^2} + 2{a^2} + 2{b^2} - {c^2}\\ \Leftrightarrow {b^2} + {c^2} = {a^2}\end{array}\)
Suy ra tam giác \(ABC\) vuông tại \(A.\)
Chọn C
Câu hỏi 25 :
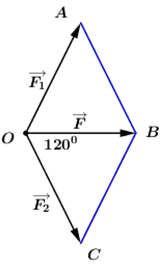
Cho ba lực \(\overrightarrow {{F_1}} = \overrightarrow {MA} ,\,\,\,\overrightarrow {{F_2}} = \overrightarrow {MB} ,\,\,{\overrightarrow F _3} = \overrightarrow {MC} \) cùng tác động vào một vật tại điểm \(M\) và vật đứng yên. Cho biết cường độ của \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) đều bằng \(50\,N\) và góc \(\angle AMB = 60^\circ \). Tính cường độ lực của \(\overrightarrow {{F_3}} .\)
- A \(50\sqrt 3 \left( N \right).\)
- B \(100\sqrt 3 \left( N \right).\)
- C \(25\sqrt 3 \left( N \right).\)
- D \(35\sqrt 3 \left( N \right).\)
Đáp án: A
Phương pháp giải:
Vật cân bằng khi tổng hợp lực lên vật bằng vecto không.
Lời giải chi tiết:
Vì vật đứng yên nên \(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = \overrightarrow 0 \)
\(\begin{array}{l} \Leftrightarrow \overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow 0 \Rightarrow \overrightarrow {MC} = - \left( {\overrightarrow {MA} + \overrightarrow {MB} } \right) = \overrightarrow {AM} + \overrightarrow {BM} \\ \Rightarrow M{C^2} = M{A^2} + M{B^2} + 2MA.MB\cos \angle \left( {\overrightarrow {AM} ,\,\,\overrightarrow {BM} } \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {50^2} + {50^2} + 2.50.50.\cos 60^\circ = 3.50^\circ \\ \Rightarrow MC = 50\sqrt 3 .\\ \Rightarrow \left| {\overrightarrow {{F_3}} } \right| = 50\sqrt 3 \,\,N.\end{array}\)
Chọn A.
Câu hỏi 26 :
Trong tam giác \(ABC,\) nếu có \({a^2} = b.c\) thì:
- A \(\frac{1}{{h_a^2}} = \frac{1}{{{h_b}}} + \frac{1}{{{h_c}}}\)
- B \(\frac{1}{{h_a^2}} = \frac{2}{{{h_b}}} + \frac{2}{{{h_c}}}\)
- C \(\frac{1}{{h_a^2}} = \frac{1}{{{h_b}}} - \frac{1}{{{h_c}}}\)
- D \(h_a^2 = {h_b}.{h_c}\)
Đáp án: D
Phương pháp giải:
Sử dụng công thức tính diện tích tam giác \(S = \frac{1}{2}a.{h_a}.\)
Lời giải chi tiết:
Ta có: \(S = \frac{1}{2}a.{h_a} \Rightarrow {h_a} = \frac{{2S}}{a}\)\( \Rightarrow h_a^2 = \frac{{4{S^2}}}{{{a^2}}} = \frac{{4{S^2}}}{{b.c}} = \frac{{2S}}{b}.\frac{{2S}}{c} = {h_b}.{h_c}\)
Chọn D.
Câu hỏi 27 :
Cho tam giác \(ABC\) có \(AB = 6,AC = 8\) và \(\angle BAC = 60^\circ .\) Tính bán kính đường tròn ngoại tiếp tam giác \(ABC\).
- A \(\frac{{\sqrt {39} }}{3}\)
- B \(\frac{{2\sqrt {39} }}{3}\)
- C \(\frac{{3\sqrt {39} }}{3}\)
- D \(\frac{{\sqrt {39} }}{2}\)
Đáp án: B
Phương pháp giải:
Áp dụng định lý hàm số sin và định lý hàm số cos trong tam giác.
Lời giải chi tiết:
Áp dụng định lý cos trong tam giác \(ABC\) ta có:
\(\begin{array}{l}B{C^2} = A{B^2} + A{C^2} - 2AB.AC\cos \angle BAC\\B{C^2} = {6^2} + {8^2} - 2.6.8.\cos {60^0}\\BC = 2\sqrt {13} .\end{array}\)
Áp dụng định lý hàm số sin trong tam giác \(ABC\) ta có:
\(\frac{{BC}}{{\sin \angle BAC}} = 2R\) (trong đó \(R\) là bán kính đường tròn ngoại tiếp tam giác \(BAC\)).
\( \Rightarrow \frac{{2\sqrt {13} }}{{\sin {{60}^0}}} = 2R \Rightarrow R = \frac{{2\sqrt {39} }}{3}.\)
Chọn B.
Câu hỏi 28 :
Trong cuộc thi giải trí toán học tổ chức nhân dịp hoạt động chào mừng Ngày nhà giáo Việt Nam có một trò chơi như sau: Người ta thiết kế hai đường ray tạo với nhau một góc \({30^o}\) như hình vẽ dưới đây. Trên các đường thẳng \(Ox,Oy\) người ta để hai vật nặng cùng trọng lượng. Buộc hai vật thể với nhau bằng một thanh cứng \(AB = 1m\) sao cho mỗi vật đều có thể chuyển động trên hai đường ray. Nối hai vật bằng một sợi dây vòng qua một cột có gốc tại \(O.\) Người thắng cuộc sẽ là người kéo được vật thể ra xa nhất so với điểm gốc \(O.\) Hãy dùng kiến thức toán học để tính vị trí xa nhất mà người tham dự cuộc thi có thể đạt được.
- A \(1m\)
- B \(\sqrt 2 m\)
- C \(\sqrt 3 m\)
- D \(2m\)
Đáp án: D
Phương pháp giải:
Ta sử dụng định lí hàm cosin vào tam giác \(OAB\) để tính \(AB\) , đánh giá biểu thức \(AB\) để tìm được vị trí xa nhất.
Lời giải chi tiết:
Đặt \(OB = x,OA = y\left( {x,y > 0} \right)\)
Theo định lí cosin ta có: \(A{B^2} = {x^2} + {y^2} - 2xy\cos {30^o} = {x^2} + {y^2} - \sqrt 3 xy\)
Theo giải thiết, ta có \(AB = 1 \Leftrightarrow {x^2} + {y^2} - \sqrt 3 xy = 1\)
Xét PT bậc hai: \({y^2} - \sqrt 3 xy + {x^2} - 1 = 0\) . Phương trình có nghiệm \(y \Leftrightarrow \Delta = 3{x^2} - 4\left( {{x^2} - 1} \right) \ge 0 \Leftrightarrow 0 < x \le 2\)
Vậy vị trí xa nhất mà học sinh có thể đạt được cách \(O\) một khoảng là \(2m.\)
Chọn D
Câu hỏi 29 :
Trong mặt phẳng cho tam giác \(ABC\) và một điểm \(M\) bất kỳ. Đặt \(a = BC,b = CA,c = AB.\) Tìm giá trị nhỏ nhất của biểu thức \(T = \frac{{MA}}{a} + \frac{{MB}}{b} + \frac{{MC}}{c}.\)
- A \(\frac{{\sqrt 3 }}{2}\)
- B \(\frac{{\sqrt 3 }}{3}\)
- C \(3\sqrt 3 \)
- D \(\sqrt 3 \)
Đáp án: D
Phương pháp giải:
Sử dụng công thức đường trung tuyến và BĐT Cô si cho ba số không âm để tìm được GTNN của biểu thức \(T = \frac{{MA}}{a} + \frac{{MB}}{b} + \frac{{MC}}{c}\) .
Lời giải chi tiết:
Theo công thức độ dài đường trung tuyến, ta có:
\(4{m_a}^2 = 2\left( {{b^2} + {c^2}} \right) - {a^2} \Rightarrow 2\left( {{b^2} + {c^2} + {a^2}} \right) = 4{m_a}^2 + 3{a^2} \ge 4\sqrt 3 a{m_a} \Rightarrow a{m_a} \le \frac{{{b^2} + {c^2} + {a^2}}}{{2\sqrt 3 }}\)
Gọi \(G\) là trọng tâm tam giác \(ABC,\) khi đó:
\(\frac{{MA}}{a} = \frac{{MA.GA}}{{a.GA}} \ge \frac{{\overrightarrow {MA} .\overrightarrow {GA} }}{{\frac{2}{3}.\frac{{{b^2} + {c^2} + {a^2}}}{{2\sqrt 3 }}}} = \frac{{3\sqrt 3 }}{{{b^2} + {c^2} + {a^2}}}\left( {\overrightarrow {MG} + \overrightarrow {GA} } \right)\overrightarrow {GA} = \frac{{3\sqrt 3 }}{{{b^2} + {c^2} + {a^2}}}\left( {\overrightarrow {MG} .\overrightarrow {GA} + G{A^2}} \right)\)
Từ đó, suy ra:
\(\frac{{MA}}{a} + \frac{{MB}}{b} + \frac{{MC}}{c} \ge \frac{{3\sqrt 3 }}{{{b^2} + {c^2} + {a^2}}}\left[ {\overrightarrow {MG} \left( {\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} } \right) + G{A^2} + G{B^2} + G{C^2}} \right]\)
Lại có: \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 ;G{A^2} + G{B^2} + G{C^2} = \frac{1}{3}\left( {{a^2} + {b^2} + {c^2}} \right)\)
Do đó \(\frac{{MA}}{a} + \frac{{MB}}{b} + \frac{{MC}}{c} \ge \frac{{3\sqrt 3 }}{{\left( {{b^2} + {a^2} + {c^2}} \right)}}\left[ {0 + \frac{1}{3}\left( {{a^2} + {b^2} + {c^2}} \right)} \right] = \sqrt 3 .\)
Đẳng thức xảy ra khi tam giác \(ABC\) đều, đồng thời \(M\) trùng với trọng tâm của tam giác \(ABC.\)
Chọn D
Câu hỏi 30 :
Cho hình thang vuông \(ABCD\), đường cao \(AD = h,\) đáy \(AB = a,\) đáy \(CD = b.\) Gọi \(M\) là trung điểm của \(BC.\) Hệ thức giữa \(a,b,h\) để \(AM \bot BD\) là:
- A \({a^2} - {h^2} - ab = 0\)
- B \({h^2} - {a^2} - ab = 0\)
- C \({h^2} - {b^2} - ab = 0\)
- D \({b^2} - {h^2} - ab = 0\)
Đáp án: B
Phương pháp giải:
+) Ta sử dụng tính chất của hai vecto vuông góc và biến đổi các vecto thông qua 3 vecto \(\overrightarrow {AB} ,\overrightarrow {AD} ,\overrightarrow {DC} \)
+) \(\overrightarrow a \) vuông góc với \(\overrightarrow b \Leftrightarrow \overrightarrow a .\overrightarrow b = 0\)
Lời giải chi tiết:
Ta có:
\(\begin{array}{l}AM \bot BD \Leftrightarrow 2.\overrightarrow {AM} .\overrightarrow {BD} = 0\\ \Leftrightarrow \left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\overrightarrow {BD} = 0\\ \Leftrightarrow \left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {DC} } \right)\left( {\overrightarrow {AD} - \overrightarrow {AB} } \right) = 0\\ \Leftrightarrow - A{B^2} + A{D^2} - \overrightarrow {DC} .\overrightarrow {AB} = 0\\ \Leftrightarrow {h^2} - {a^2} - ab = 0\end{array}\)
Chọn B.
Câu hỏi 31 :
Các cạnh của tam giác ABC thỏa mãn hệ thức \({a^4} + {b^4} = {c^4}\). Khẳng định nào sau đây đúng.
- A Tam giác ABC là tam giác tù.
- B Tam giác ABC là tam giác nhọn.
- C Tam giác ABC là tam giác vuông.
- D Tam giác ABC là tam giác đều.
Đáp án: B
Phương pháp giải:
Sử dụng công thức định lí hàm cosin: \({c^2} = {a^2} + {b^2} - 2ab\,cosC\).
Lời giải chi tiết:
Từ giả thiết ta có \({a^4} + {b^4} = {c^4} \Rightarrow \left\{ \matrix{ {c^4} > {a^4} \hfill \cr {c^4} > {b^4} \hfill \cr} \right. \Rightarrow \left\{ \matrix{ c > a \hfill \cr c > b \hfill \cr} \right. \Rightarrow \left\{ \matrix{ \widehat C > \widehat A \hfill \cr \widehat C > \widehat B \hfill \cr} \right.\,\,\,\,\,\,\,\,\,\left( 1 \right).\)
Mặt khác, từ giả thiết ta cũng có:
\(\eqalign{ & {\left( {{a^2} + {b^2}} \right)^2} - 2{a^2}{b^2} = {a^4} + {b^4} = {c^4} \Leftrightarrow {\left( {{a^2} + {b^2}} \right)^2} - {c^4} = 2{a^2}{b^2} \Leftrightarrow \left( {{a^2} + {b^2} - {c^2}} \right)\left( {{a^2} + {b^2} + {c^2}} \right) = 2{a^2}{b^2} \cr & \Leftrightarrow {{{a^2} + {b^2} - {c^2}} \over {2ab}} = {{ab} \over {{a^2} + {b^2} + {c^2}}} \Leftrightarrow \cos C = {{ab} \over {{a^2} + {b^2} + {c^2}}} > 0 \Rightarrow C < {90^0}\,\,\,\,\,\,\,\,\,\left( 2 \right). \cr} \)
Kết hợp (1) và (2) ta có tam giác ABC có 3 góc nhọn.
Chọn B.
Câu hỏi 32 :
Các cạnh của tam giác ABC thỏa mãn hệ thức \({a^4} + {b^4} = {c^4}\). Khẳng định nào sau đây đúng.
- A \(2{\cos ^2}C = \tan A.\tan B\).
- B \(2{\sin ^2}C = \tan A.\tan B\).
- C \(2{\tan ^2}C = \tan A.\tan B\).
- D \(2{\cot ^2}C = \tan A.\tan B.\)
Đáp án: B
Phương pháp giải:
Áp dụng công thức cosin \(\eqalign{ & {a^2} = {b^2} + {c^2} - 2bc\,CosA \cr & {b^2} = {a^2} + {c^2} - 2ac\,CosB \cr} \) và công thức tính diện tích \(S = {1 \over 2}bc\sin A = {1 \over 2}ac\sin B = {1 \over 2}ab\sin C\)
Lời giải chi tiết:
Từ giả thiết ta có:
\(\eqalign{ & {a^4} + {b^4} = {c^4} \Leftrightarrow {\left( {{a^2} - {b^2}} \right)^2} + 2{a^2}{b^2} = {c^4} \Leftrightarrow {c^4} - {\left( {{a^2} - {b^2}} \right)^2} = 2{a^2}{b^2} \cr & \Leftrightarrow \left( {{c^2} - {a^2} + {b^2}} \right)\left( {{c^2} + {a^2} - {b^2}} \right) = 2{a^2}{b^2} \cr} \)
\( \Leftrightarrow {{{c^2} - {a^2} + {b^2}} \over {4S}}.{{{c^2} + {a^2} - {b^2}} \over {4S}} = {2 \over 4}.{\left( {{{ab} \over {2S}}} \right)^2}\) (*)
Áp dụng công thức cosin và công thức tính diện tích \(S = {1 \over 2}bc\sin A = {1 \over 2}ac\sin B = {1 \over 2}ab\sin C\) ta có
(*) \( \Leftrightarrow {{2bc\cos A} \over {2bc\sin A}}.{{2ac\cos B} \over {2ac\sin B}} = {2 \over 4}.{\left( {{{ab} \over {ab\sin C}}} \right)^2}\)
\( \Leftrightarrow \cot A.\cot B = {1 \over {2{{\sin }^2}C}} \Leftrightarrow {1 \over {\tan A}}.{1 \over {\tan B}} = {1 \over {2{{\sin }^2}C}} \Leftrightarrow \tan A.\tan B = 2{\sin ^2}C\)
Chọn B
Câu hỏi 33 :
Cho góc \(\widehat {xOy} = {30^0}\). Gọi A và B là hai điểm di động lần lượt trên Ox và Oy sao cho AB = 1. Độ dài lớn nhất của đoạn OB bằng:
- A 1,5
- B \(\sqrt 3 \)
- C \(2\sqrt 2 \)
- D 2
Đáp án: D
Phương pháp giải:
Sử dụng công thức định lý cosin và áp dụng điều kiện có nghiệm của phương trình bậc hai.
Lời giải chi tiết:
Sử dụng công thức định lý cosin ta có
\(A{B^2} = O{A^2} + O{B^2} - 2OA.OB.\cos \widehat {AOB}\)
Theo giả thiết ta có
\(1 = O{A^2} + O{B^2} - 2OA.OB.\cos {30^0 }\)
\( \Leftrightarrow 1 = O{A^2} + O{B^2} - \sqrt 3 OA.OB.\)
Coi biểu thức là phương trình bậc hai đối với OA và tham số OB có
\(O{A^2} - \sqrt 3 OB.OA + O{B^2} - 1 = 0\)
Để phương trình có nghiệm thì \(\Delta = {\left( {\sqrt 3 OB} \right)^2} - 4\left( {O{B^2} - 1} \right) \ge 0 \Leftrightarrow 4 - O{B^2} \ge 0 \Leftrightarrow OB \le 2\)
Chọn D
Câu hỏi 34 :
Xác định dạng của tam giác \(ABC\) biết rằng \(S = {{\sqrt 3 } \over {36}}{\left( {a + b + c} \right)^2}\).
- A Tam giác tù
- B Tam giác vuông
- C Tam giác đều
- D Chưa đủ điều kiện để kết luận
Đáp án: C
Phương pháp giải:
Sử dụng các công thức tính diện tích tam giác, đẳng thức với vế phải \(a + b + c\) liên tưởng tới công thức chứa nửa chu vi p.
Lời giải chi tiết:
Theo công thức He-rong ta có
\(\sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} = {{\sqrt 3 } \over 9}{p^2} \Leftrightarrow \left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right) = {1 \over {27}}{p^3}\)
Theo bất đẳng thức Cauchy ta có \(\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right) \le {{{{\left( {p - a + p - b + p - c} \right)}^3}} \over {27}} = {{{{\left( {3p - \left( {a + b + c} \right)} \right)}^3}} \over {27}} = {{{{\left( {3p - 2p} \right)}^3}} \over {27}} = {{{p^3}} \over {27}}\)
Đẳng thức xảy ra khi a = b = c.
Khi đó tam giác \(ABC\) đều.
Chọn C.
Câu hỏi 35 :
Xác định hình dạng tam giác \(ABC\) biết \(\left\{ \matrix{ {{{b^3} + {c^3} - {a^3}} \over {b + c - a}} = {a^2} \hfill \cr a = 2b\cos C \hfill \cr} \right.\)
- A Tam giác tù
- B Tam giác vuông
- C Tam giác đều
- D Chưa đủ điều kiện để kết luận
Đáp án: C
Phương pháp giải:
Sử dụng định lí cosin trong tam giác chỉ ra các đẳng thức liên hệ
Lời giải chi tiết:
Theo định lí cosin ta có \({\mathop{\rm cosC}\nolimits} = {{{a^2} + {b^2} - {c^2}} \over {2ab}}\), thay vào đẳng thức thứ hai của hệ trên ta có
\(a = 2b{\mathop{\rm cosC}\nolimits} = 2b.{{{a^2} + {b^2} - {c^2}} \over {2ab}} \Rightarrow {a^2} = {a^2} + {b^2} - {c^2} \Leftrightarrow {b^2} - {c^2} = 0 \Leftrightarrow {b^2} = {c^2} \Rightarrow b = c\)
Thay b = c vào hệ thức thứ nhất ta có \({{2{b^3} - {a^3}} \over {2b - a}} = {a^2} \Leftrightarrow 2{b^3} - {a^3} = 2b{a^2} - {a^3} \Leftrightarrow {b^2} = {a^2} \Rightarrow a = b\).
Do đó a = b = c. Vậy tam giác \(ABC\) đều.
Chọn C.
Câu hỏi 36 :
Cho tam giác ABC vuông tại A có AB = 5cm, BC = 13cm. Gọi góc \(\widehat {ABC} = \alpha \) và\(\widehat {ACB} = \beta \). Hãy chọn kết luận đúng khi so sánh \(\alpha \) và \(\beta \).
- A \(\beta > \alpha \)
- B \(\beta < \alpha \)
- C \(\beta = \alpha \)
- D \(\alpha \le \beta \)
Đáp án: B
Phương pháp giải:
+ Sử dụng định lý Pitago \(B{C^2} = A{B^2} + A{C^2}\) để tính AC.
+ Sử dụng công thức định lí sin là:\({b \over {\sin B}} = {c \over {\sin C}}\)
+ Sử dụng nhận xét khi \(x \in (0,{90^0 }\) thì hàm \(y = \sin x\) đồng biến và \(\sin x > 0\).
Lời giải chi tiết:
+ Có \(AC = \sqrt {B{C^2} - A{B^2}} = \sqrt {{{13}^2} - {5^2}} = 12\).
+ \({b \over {\sin B}} = {c \over {\sin C}} \Rightarrow {{\sin C} \over {\sin B}} = {c \over b} = {5 \over {12}} < 1\) (*)
+ Tam giác ABC vuông tại A, suy ra B và C là góc nhọn. Do đó \(\sin B > 0\) và \(\sin C > 0\). Từ (*) suy ra \(\sin C < \sin B\) . Suy ra C < B hay \(\beta < \alpha \).
Chọn B.
Câu hỏi 37 :
Trong tam giác ABC có
- A \({m_a} = {{b + c} \over 2}\)
- B \({m_a} < {{b + c} \over 2}\)
- C \({m_a} > {{b + c} \over 2}\)
- D \({m_a} = b + c\)
Đáp án: B
Phương pháp giải:
Sử dụng công thức trung tuyến \(m_a^2 = {{{b^2} + {c^2}} \over 2} - {{{a^2}} \over 4}\) và xét hiệu \(m_a^2 - {\left( {{{b + c} \over 2}} \right)^2}\).
Lời giải chi tiết:
Ta có:
\(m_a^2 - {\left( {{{b + c} \over 2}} \right)^2} = {{{b^2} + {c^2}} \over 2} - {{{a^2}} \over 4} - {{{b^2} + {c^2} + 2bc} \over 4} = {{{b^2} + {c^2} - {a^2} - 2bc} \over 4} = {{{{(b - c)}^2} - {a^2}} \over 4}\)
Trong tam giác ta có \(|b - c| < a\) suy ra \({(b - c)^2} < {a^2}\). Do đó \({{{{(b - c)}^2} - {a^2}} \over 4} < 0 \Rightarrow m_a^2 - {\left( {{{b + c} \over 2}} \right)^2} < 0\).
Vậy \({m_a} < {{b + c} \over 2}\).
Chọn B.
Câu hỏi 38 :
Tam giác ABC vuông cân tại A và nội tiếp trong đường tròn tâm O bán kính R. Gọi r là bán kính đường tròn nội tiếp tam giác ABC. Khi đó tỉ số \({R \over r}\) bằng:
- A \(1 + \sqrt 2 \)
- B \({{2 + \sqrt 2 } \over 2}\)
- C \({{\sqrt 2 - 1} \over 2}\)
- D \({{1 + \sqrt 2 } \over 2}\)
Đáp án: A
Phương pháp giải:
Sử dụng các công thức tính diện tích của tam giác
\(\eqalign{ & S = {1 \over 2}a{h_a} = {1 \over 2}b{h_b} = {1 \over 2}c{h_c} \cr & S = {{abc} \over {4R}} \cr & S = p.r \cr} \)
Lời giải chi tiết:
Tam giác ABC vuông cân tại A, giả sử có AB = AC = a.
Theo định lý Pi – ta – go ta có \(BC = \sqrt 2 a\). Suy ra \(p = = {{a + a + a\sqrt 2 } \over 2} = {{\left( {2 + \sqrt 2 } \right)a} \over 2}\)
+) Ta có \(S = {1 \over 2}AB.AC = {1 \over 2}{a^2}\)
+) Ta có \(R = {{abc} \over {4S}} = {{\sqrt 2 {a^3}} \over {2{a^2}}} = {{\sqrt 2 a} \over 2}\).
+) Ta có \(r = {S \over p} = {{{1 \over 2}{a^2}} \over { = {{\left( {2 + \sqrt 2 } \right)a} \over 2}}} = {a \over {2 + \sqrt 2 }}\)
Suy ra \({R \over r} = {{\sqrt 2 } \over 2}a.{{2 + \sqrt 2 } \over a} = {{2\sqrt 2 + 2} \over 2} = \sqrt 2 + 1\)
Chọn A.
Câu hỏi 39 :
Cho hai lực \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) có cùng điểm đặt tại O. Biết \(\overrightarrow {{F_1}} \), \(\overrightarrow {{F_2}} \) đều có cường độ là 100N, góc hợp bởi \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) bằng 1200 . Cường độ lực tổng hợp của chúng là :
- A \(200N\)
- B \(50\sqrt 3 N\)
- C \(100\sqrt 3 N\)
- D \(100N\)
Đáp án: D
Phương pháp giải:
Áp dụng quy tắc hình bình hành.
Lời giải chi tiết:
Dựng hình thoi OABC sao cho \(\angle AOC = {120^o} \Rightarrow {\overrightarrow F _1} = \overrightarrow {OA} ;\,\,\,\overrightarrow {{F_2}} = \overrightarrow {OC} \)
\( \Rightarrow {\overrightarrow F _1} + \overrightarrow {{F_2}} = \overrightarrow {OA} + \overrightarrow {OC} = \overrightarrow {OB} \)
OABC là hình thoi \(\angle AOC = {120^o} \Rightarrow \angle OAB = {60^o} \Rightarrow \Delta AOB\) là tam giác
đều \( \Rightarrow OB = 100 \Rightarrow \left| {\overrightarrow F } \right| = 100\;N.\)
Chọn D.
Câu hỏi 40 :
Cho tam giác DEF biết: Có \(\angle D = {90^o},DE = 3,DF = 4\), I là trung điểm của DE. Tính bán kính đường tròn ngoại tiếp\(\Delta IEF\).
- A \(R = \frac{{5\sqrt {73} }}{{16}}\)
- B \(R = \frac{{5\sqrt {73} }}{8}\)
- C \(R = \frac{{5\sqrt {73} }}{4}\)
- D \(R = \frac{{5\sqrt {73} }}{2}\)
Đáp án: A
Phương pháp giải:
Sử dụng định lý sin: \(\frac{a}{{\sin \angle A}} = \frac{b}{{\sin \angle B}} = \frac{c}{{\sin \angle C}} = 2R\) (\(R\) là bán kính đường tròn ngoại tiếp tam giác)
Lời giải chi tiết:
Áp dụng định lý Pi-ta-go cho tam giác DEF vuông tại D:
\(EF = \sqrt {D{E^2} + D{F^2}} = \sqrt {{3^2} + {4^2}} = 5\)
I là trung điểm của DE \( \Rightarrow DI = \frac{1}{2}DE = \frac{3}{2}\)
Áp dụng định lý Pi-ta-go cho tam giác DIF vuông tại D:
\(IF = \sqrt {D{I^2} + D{F^2}} = \sqrt {{{\left( {\frac{3}{2}} \right)}^2} + {4^2}} = \frac{{\sqrt {73} }}{2}\)
Xét tam giác DEF vuông tại D \( \Rightarrow \sin \angle E = \frac{{DF}}{{EF}} = \frac{4}{5}\)
Áp dụng định lý hàm số sin trong tam giác IEF ta được:
\(2R = \frac{{IF}}{{\sin \angle E}} = \frac{{\sqrt {73} .5}}{{2.4}} = \frac{{5\sqrt {73} }}{8} \Rightarrow R = \frac{{5\sqrt {73} }}{{16}}\)
Chọn A.
>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10
 |
 |
 |
 |
 |
 |
 |
 |
Các bài khác cùng chuyên mục