30 bài tập trắc nghiệm phép tịnh tiến
Làm đề thiCâu hỏi 1 :
Cho phép biến hình F có quy tắc đặt ảnh tương ứng điểm \(M\left( {{x_M};{y_M}} \right)\) có ảnh là điểm \(M'\left( {x';y'} \right)\) theo công thức: \(F:\,\,\left\{ \begin{array}{l}x' = {x_M} - 1\\y' = {y_M} + 2\end{array} \right.\). Tìm tọa độ điểm \(A'\) là ảnh của điểm \(A\left( {1;2} \right)\) qua phép biến hình F.
- A \(A'\left( {1;4} \right)\)
- B \(A'\left( {2;0} \right)\)
- C \(A'\left( {1; - 2} \right)\)
- D \(A'\left( {0;4} \right)\)
Đáp án: D
Phương pháp giải:
Thay số vào quy tắc đề bài cho.
Lời giải chi tiết:
Theo quy tắc ta có \(\left\{ \begin{array}{l}x' = {x_M} - 1 = 1 - 1 = 0\\y' = {y_M} + 2 = 2 + 2 = 4\end{array} \right. \Rightarrow A'\left( {0;4} \right).\)
Chọn D.
Câu hỏi 2 :
Ta nói M là điểm bất động qua phép biến hình f nghĩa là:
- A M không biến thành điểm nào
- B M biến thành vô số điểm
- C \(f\left( M \right) = M\)
- D . M biến thành một điểm vô cùng xa
Đáp án: C
Phương pháp giải:
Điểm bất động qua phép biến hình là điểm mà có ảnh qua phép biến hình đó là chính nó.
Lời giải chi tiết:
Ta nói M là điểm bất động qua phép biến hình f nghĩa là: \(f\left( M \right) = M\).
Chọn C.
Câu hỏi 3 :
Trong mặt phẳng tọa độ \(Oxy\), tọa độ ảnh \(A'\) của điểm \(A\left( {1;3} \right)\) qua phép tịnh tiến theo véc tơ \(\overrightarrow v \left( {2;3} \right)\) là điểm nào trong các điểm sau đây?
- A \(A'\left( {4;3} \right)\)
- B \(A'\left( {0;2} \right)\)
- C \(A'\left( {1;0} \right)\)
- D \(A'\left( {3;6} \right)\)
Đáp án: D
Phương pháp giải:
\({T_{\overrightarrow u }}\) biến \(M\left( {x;y} \right)\) thành \(M'\left( {x';y'} \right) \Rightarrow \left\{ \begin{array}{l}x' = x + a\\y' = y + b\end{array} \right.\).
Lời giải chi tiết:
\({T_{\overrightarrow v }}\left( A \right) = A' \Rightarrow \left\{ \begin{array}{l}{x_{A'}} = 1 + 2 = 3\\{y_{A'}} = 3 + 3 = 6\end{array} \right. \Rightarrow A'\left( {3;6} \right)\).
Chọn D.
Câu hỏi 4 :
Trong mặt phẳng tọa độ \(Oxy\), cho vecto \(\overrightarrow v = \left( { - 2;3} \right)\) và đường thẳng \(d:3x - 5y + 3 = 0.\) Viết phương trình của đường thẳng \(d'\) là ảnh của d qua phép tịnh tiến vecto \(\overrightarrow v .\)
- A \(3x - 5y + 2 = 0\)
- B \(3x - 5y - 24 = 0\)
- C \(3x - 5y + 24 = 0\)
- D \(3x - 4y - 2 = 0\)
Đáp án: C
Lời giải chi tiết:
Chọn \(A\left( { - 1;0} \right) \in d:3x - 5y + 3 = 0\)
Tọa độ điểm \(A'\) là ảnh của \(A\) qua \({T_{\overrightarrow v }}\) là: \(\left\{ \begin{array}{l}x' = - 1 - 2 = - 3\\y' = 0 + 3 = 3\end{array} \right.\)\( \Rightarrow A'\left( { - 3;3} \right).\)
Phương trình đường thẳng có dạng: \(3x - 5y + c = 0\)
Thay \(3x - 5y + c = 0\) vào \(d'\) ta có: \( - 9 - 15 + c = 0\)\( \Leftrightarrow c = 24\).
Vậy phương trình đường thẳng \(d'\) là: \(3x - 5y + 24 = 0.\)
Chọn C.
Câu hỏi 5 :
Trong mặt phẳng Oxy, cho \(\overrightarrow u = \left( {2; - 1} \right)\), điểm \(M\left( {3;2} \right)\). Tìm tọa độ điểm A sao cho \(M = {T_{\overrightarrow u }}\left( A \right)\).
- A \(A\left( { - 1;3} \right)\)
- B \(A\left( {1;3} \right)\)
- C \(A\left( {1; - 3} \right)\)
- D \(A\left( { - 1; - 3} \right)\)
Đáp án: B
Lời giải chi tiết:
\(\begin{array}{l}A\left( {x;y} \right);\,\,M\left( {3;2} \right);\,\,\overrightarrow u \left( {2; - 1} \right)\\M = {T_{\overrightarrow u }}\left( A \right) \Rightarrow \left\{ \begin{array}{l}{x_A} = 3 - 2 = 1\\{y_A} = 2 - \left( { - 1} \right) = 3\end{array} \right. \Rightarrow A\left( {1; 3} \right)\end{array}\)
Chọn B.
Câu hỏi 6 :
Cho hình bình hành \(ABCD\). Ảnh của điểm \(D\) qua phép tịnh tiến theo \(\overrightarrow {AB} \) là:
- A \(B\)
- B \(C\)
- C \(D\)
- D \(A\)
Đáp án: B
Phương pháp giải:
Sử dụng định nghĩa phép tịnh tiến: \({T_{\overrightarrow v }}\left( M \right) = M' \Leftrightarrow \overrightarrow {MM'} = \overrightarrow v \).
Lời giải chi tiết:
Do \(ABCD\) là hình bình hành nên \(\overrightarrow {AB} = \overrightarrow {DC} \Rightarrow {T_{\overrightarrow {AB} }}\left( D \right) = C\).
Chọn B.
Câu hỏi 7 :
Trong mặt phẳng tọa độ \(Oxy\), phép tịnh tiến theo \(\overrightarrow v \) biến điểm \(M\left( {x;y} \right)\) thành điểm \(M'\left( {x';y'} \right)\) sao cho \(x' = x - 2;\,\,y' = y + 4\). Tọa độ của \(\overrightarrow v \) là:
- A \(\overrightarrow v = \left( { - 2;4} \right)\)
- B \(\overrightarrow v = \left( {4; - 2} \right)\)
- C \(\overrightarrow v = \left( { - 2; - 4} \right)\)
- D \(\overrightarrow v = \left( {2;4} \right)\)
Đáp án: A
Phương pháp giải:
Sử dụng biểu thức tọa độ của phép tịnh tiến.
\({T_{\overrightarrow v }}\left( M \right) = M'\) với \(M\left( {x;y} \right);\,\,M'\left( {x';y'} \right);\,\,\overrightarrow v \left( {a;b} \right)\) thì \(\left\{ \begin{array}{l}x' = x + a\\y' = y + b\end{array} \right.\).
Lời giải chi tiết:
Ta có \(\left\{ \begin{array}{l}x' = x - 2\\y' = y + 4\end{array} \right. \Rightarrow \overrightarrow v = \left( { - 2;4} \right)\).
Chọn A.
Câu hỏi 8 :
Cho phép tịnh tiến theo \(\overrightarrow v = \overrightarrow 0 \), phép tịnh tiến \({T_{\overrightarrow 0 }}\) biến hai điểm phân biệt \(M\) và \(N\) thành 2 điểm \(M'\) và \(N'\), khi đó :
- A Điểm \(M\) trùng với điểm \(N\)
- B Vectơ \(\overrightarrow {MN} \) là vectơ \(\overrightarrow 0 \)
- C \(\overrightarrow {MM'} = \overrightarrow {NN'} = \overrightarrow 0 \)
- D \(\overrightarrow {MM'} \ne \overrightarrow 0 \)
Đáp án: C
Phương pháp giải:
Phép tịnh tiến theo \(\overrightarrow 0 \) là phép đồng nhất, tức là \({T_{\overrightarrow 0 }}\left( M \right) = M\).
Lời giải chi tiết:
\(\left\{ \begin{array}{l}{T_{\overrightarrow 0 }}\left( M \right) = M' \Leftrightarrow \overrightarrow {MM'} = 0\\{T_{\overrightarrow 0 }}\left( N \right) = N' \Leftrightarrow \overrightarrow {NN'} = 0\end{array} \right. \Rightarrow \overrightarrow {MM'} = \overrightarrow {NN'} = \overrightarrow 0 \).
Chọn C.
Câu hỏi 9 :
Cho lục giác đều \(ABCDEF\) có tâm \(O\). Phép tịnh tiến theo véc tơ \(\overrightarrow {BO} \) biến điểm \(O\) thành điểm nào?
- A Điểm \(F\)
- B Điểm \(D\)
- C Điểm \(E\)
- D Điểm \(B\)
Đáp án: C
Phương pháp giải:
Dựng hình, tìm ảnh của \(O\) qua phép tịnh tiến theo véc tơ \(\overrightarrow {BO} \).
Sử dụng định nghĩa: \({T_{\overrightarrow v }}\left( M \right) = M' \Leftrightarrow \overrightarrow {MM'} = \overrightarrow v \).
Lời giải chi tiết:
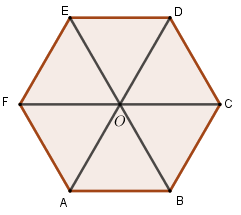
Quan sát hình vẽ ta thấy \({T_{\overrightarrow {BO} }}\left( O \right) = E\) vì \(\overrightarrow {OE} = \overrightarrow {BO} \).
Chọn C
Câu hỏi 10 :
Trong mặt phẳng với hệ tọa độ \(Oxy\), cho hai đường thẳng \(\left( {{d_1}} \right):\,\,2x + 3y + 1 = 0\) và \(\left( {{d_2}} \right):\,\,x - y - 2 = 0\). Có bao nhiêu phép tịnh tiến biến \({d_1}\) thành \({d_2}\).
- A Vô số
- B 4
- C 1
- D 0
Đáp án: D
Phương pháp giải:
Sử dụng tính chất của phép tịnh tiến: Phép tịnh tiến biến một đườn tghẳng thành đường thẳng song song hoặc trùng với nó.
Lời giải chi tiết:
Ta có \(\dfrac{2}{1} \ne \dfrac{3}{{ - 1}} \Rightarrow {d_1}\) và \({d_2}\) cắt nhau.
Do đó không có phép tịnh tiến nào biến đường thẳng \({d_1}\) thành \({d_2}\).
Chọn D.
Câu hỏi 11 :
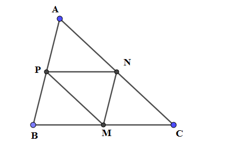
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm của các cạnh BC, CA, AB. Phát biểu nào sau đây SAI?
- A Phép tịnh tiến theo vectơ \(\overrightarrow {AP} \) biến tam giác APN thành tam giác PBM.
- B Phép tịnh tiến theo vectơ \(\dfrac{1}{2}\overrightarrow {AC} \) biến tam giác APN thành tam giác NMC.
- C Phép tịnh tiến theo vectơ \(\overrightarrow {PN} \) biến tam giác BPM thành tam giác MNC.
- D Phép tịnh tiến theo vectơ \(\overrightarrow {BP} \) biến tam giác PMN thành tam giác APN.
Đáp án: D
Lời giải chi tiết:
Phát biểu SAI là: Phép tịnh tiến theo vectơ \(\overrightarrow {BP} \) biến tam giác PMN thành tam giác APN.
Chọn: D
Câu hỏi 12 :
Phép tịnh tiến theo \(\overrightarrow v = \left( {3; - 5} \right)\), điểm \(M\left( {5; - 3} \right)\) là ảnh của điểm có tọa độ?
- A \(N\left( {1;2} \right)\)
- B \(N\left( { - 2; - 1} \right)\)
- C \(N\left( {8; - 8} \right)\)
- D \(N\left( {2;2} \right)\)
Đáp án: D
Phương pháp giải:
Biểu thức tọa độ của phép tịnh tiến theo \(\overrightarrow v \left( {a;b} \right)\) là \(\left\{ \begin{array}{l}x' = x + a\\y' = y + b\end{array} \right.\).
Lời giải chi tiết:
\(M = {T_{\overrightarrow v }}\left( N \right) \Rightarrow M\left( {5 - 3; - 3 + 5} \right) \Rightarrow N\left( {2;2} \right)\).
Chọn D.
Câu hỏi 13 :
Cho hai đường thẳng cắt nhau d và d’. Có bao nhiêu phép tịnh tiến biến đường thẳng d thành đường thẳng d’ ?
- A Có một phép duy nhất.
- B Chỉ có hai phép.
- C Có vô số phép.
- D Không có phép nào.
Đáp án: D
Phương pháp giải:
Sử dụng khái niệm phép tịnh tiến.
Lời giải chi tiết:
Hai đường thẳng cắt nhau d và d’ \( \Rightarrow \) Không có phép tịnh tiến biến đường thẳng d thành đường thẳng d’.
Chọn: D
Câu hỏi 14 :
Cho hình bình hành ABCD. Phép tịnh tiến \({T_{\overrightarrow {DA} }}\) biến:
- A B thành C
- B C thành B
- C C thành A.
- D A thành D.
Đáp án: B
Phương pháp giải:
\({T_{\overrightarrow u }}\left( M \right) = M' \Leftrightarrow \overrightarrow {MM'} = \overrightarrow u \)
Lời giải chi tiết:
Ta có \(\overrightarrow {DA} = \overrightarrow {CB} \Rightarrow {T_{\overrightarrow {DA} }}\left( C \right) = B\).
Chọn đáp án B.
Câu hỏi 15 :
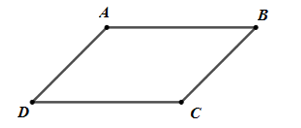
Cho hình bình hành ABCD, biết A, B cố định, điểm C di động trên đường thẳng \(\Delta \) cố định. Khẳng định nào sau đây đúng?
- A Điểm D di động trên đường thẳng \(\Delta '\) là ảnh của \(\Delta \) qua phép đối xứng trục \(AB\).
- B Điểm D di động trên đường thẳng \(\Delta '\) là ảnh của \(\Delta \) qua phép tịnh tiến theo \(\overrightarrow {BA} \).
- C Điểm D di động trên đường thẳng \(\Delta '\) là ảnh của \(\Delta \) qua phép đối xứng tâm I (I là trung điểm của AB).
- D
Điểm D di động trên đường thẳng \(\Delta '\) là ảnh của \(\Delta \) qua phép tịnh tiến theo \(\overrightarrow {AB} \).
Đáp án: B
Phương pháp giải:
Phép tịnh tiến biến đường thẳng thành đường thẳng song song với nó.
Lời giải chi tiết:
Điểm D di động trên đường thẳng \(\Delta '\) là ảnh của \(\Delta \) qua phép tịnh tiến theo \(\overrightarrow {BA} \).
Chọn: B
Câu hỏi 16 :
Có bao nhiêu phép tịnh tiến biến một đường tròn thành chính nó?
- A 3
- B 0
- C 2
- D 1
Đáp án: D
Phương pháp giải:
Phép tịnh tiến theo \(\overrightarrow{v}\) biến điểm M thành M’ \(\Leftrightarrow \overrightarrow{MM'}=\overrightarrow{v}\)
Lời giải chi tiết:
Phép tịnh tiến biến (O; R) thành chính nó là phép tịnh tiến theo vector \(\overrightarrow{0}\).
Chọn D.
Câu hỏi 17 :
Cho hình thoi ABCD tâm I. Phép tịnh tiến theo vectơ \(\overrightarrow {IA} \) biến điểm C thành điểm nào?
- A Điểm I.
- B Điểm C.
- C Điểm D.
- D Điểm B.
Đáp án: A
Phương pháp giải:
Phép tịnh tiến theo vectơ \(\overrightarrow v \) biến điểm M thành điểm M’ thỏa mãn: \(\overrightarrow {MM'} = \overrightarrow v \).
Lời giải chi tiết:
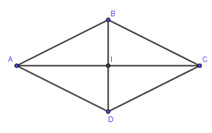
Ta có: \(\overrightarrow {IA} = \overrightarrow {CI} \Rightarrow \) Phép tịnh tiến theo vectơ \(\overrightarrow {IA} \) biến điểm C thành điểm I.
Chọn: A
Câu hỏi 18 :
Khẳng định nào sau đây là đúng về phép tịnh tiến?
- A Phép tịnh tiến theo vectơ \(\overrightarrow v \) là điểm biến điểm \(M\) thành điểm \(M'\) thì \(\overrightarrow {M'M} = \overrightarrow v \).
- B Nếu \({T_{\overrightarrow v }}\left( M \right) = M',\,{T_{\overrightarrow v }}\left( N \right) = N'\) thì \(MM'N'N\)là hình bình hành.
- C Phép tịnh tiến theo vectơ \(\overrightarrow v \) là phép đồng nhất nếu \(\overrightarrow v \) là vectơ \(\overrightarrow 0 \).
- D Phép tịnh tiến theo vectơ biến một đường thẳng thành một đường thẳng song song nó.
Đáp án: C
Phương pháp giải:
Sử dụng khái niệm và các tính chất của phép tịnh tiến.
Lời giải chi tiết:
Chọn: C
Câu hỏi 19 :
Trong không gian với hệ tọa độ Oxy, viết phương trình đường thẳng \(\Delta '\) là ảnh của đường thẳng \(\Delta :\,\,x + y - 1 = 0\) qua phép tịnh tiến theo vectơ \(\overrightarrow v \left( {2;1} \right)\).
- A \(\Delta ':\,\,x + y - 3 = 0\)
- B \(\Delta ':\,\,x + y - 4 = 0\)
- C \(\Delta ':\,\,x + y - 1 = 0\)
- D \(\Delta ':\,\,x + y + 2 = 0\)
Đáp án: B
Phương pháp giải:
- Vì \(\Delta '\parallel \Delta \) nên phương trình \(\Delta '\) có dạng: \(x + y + c = 0\).
- Chọn điểm A bất kì thuộc \(\Delta \), tìm ảnh A’ của A qua phép tịnh tiến theo vectơ \(\overrightarrow v \left( {2;1} \right)\).
- Thay tọa độ điểm A’ vào phương trình đường thẳng \(\Delta '\) tìm c.
Lời giải chi tiết:
Ta có: \({T_{\overrightarrow v }}\left( \Delta \right) = \Delta ' \Rightarrow \) \(\Delta '\parallel \Delta \) nên phương trình \(\Delta '\) có dạng: \(x + y + c = 0\).
Chọn \(A\left( {1;0} \right) \in \Delta \), gọi \(A' = {T_{\overrightarrow v }}\left( A \right) \Rightarrow \left\{ \begin{array}{l}{x_{A'}} = 1 + 2 = 3\\{y_{A'}} = 0 + 1 = 1\end{array} \right. \Rightarrow A'\left( {3;1} \right)\).
Vì \(A' \in \Delta ' \Rightarrow 3 + 1 + c = 0 \Leftrightarrow c = - 4\).
Vậy phương trình \(\Delta ':\,\,x + y - 4 = 0\).
Chọn B.
Câu hỏi 20 :
Trong không gian với hệ tọa độ Oxy, viết phương trình đường tròn (C’) là ảnh của đường tròn \(\left( C \right):\,\,{x^2} + {y^2} - 4x + 2y + 1 = 0\) qua phép tịnh tiến theo vectơ \(\overrightarrow v \left( {1;3} \right)\).
- A \(\left( {C'} \right):\,\,{\left( {x - 3} \right)^2} + {\left( {y - 2} \right)^2} = 2\)
- B \(\left( {C'} \right):\,\,{\left( {x - 3} \right)^2} + {\left( {y - 4} \right)^2} = 4\)
- C \(\left( {C'} \right):\,\,{\left( {x + 3} \right)^2} + {\left( {y + 4} \right)^2} = 4\)
- D \(\left( {C'} \right):\,\,{\left( {x - 3} \right)^2} + {\left( {y - 2} \right)^2} = 4\)
Đáp án: D
Phương pháp giải:
- Xác định tâm I và bán kính R của đường tròn (C).
- Gọi \(I' = {T_{\overrightarrow v }}\left( I \right)\), tìm tọa độ I’.
- Đường tròn (C’) là ảnh của (C) có tâm I’ và bán kính R, viết phương trình đường tròn.
Lời giải chi tiết:
Đường tròn (C) có tâm I(2;-1), bán kính \(R = \sqrt {4 + 1 - 1} = 2.\)
Gọi \(I' = {T_{\overrightarrow v }}\left( I \right)\), ta có \(\left\{ \begin{array}{l}{x_{I'}} = 2 + 1 = 3\\{y_{I'}} = - 1 + 3 = 2\end{array} \right. \Rightarrow I'\left( {3;2} \right)\).
Vì (C’) là ảnh của (C) qua phép tịnh tiến theo \(\overrightarrow v \left( {1;3} \right)\) nên (C’) là đường tròn có tâm I’(3;2), bán kính R’ = R = 2.
Vậy phương trình đường tròn (C’) là: \(\left( {C'} \right):\,\,{\left( {x - 3} \right)^2} + {\left( {y - 2} \right)^2} = 4\).
Chọn D.
Câu hỏi 21 :
Cho tam giác \(ABC\)có \(G\) là trọng tâm. Xác định ảnh của tam giác \(ABC\) qua phép tịnh tiến theo vecto \(\overrightarrow {AG} .\) Xác định điểm \(D\)sao cho phép tịnh tiến theo vecto \(\overrightarrow {AG} \) biến \(D\) thành \(A\)?
Lời giải chi tiết:
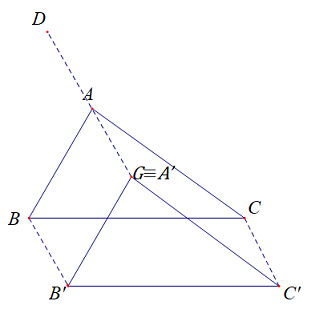
\( + )\) Xét \(\Delta ABC\): \(\left\{ \begin{array}{l}{T_{\overrightarrow {AG} }}\left( A \right) = A' \Rightarrow A' \equiv G\\{T_{\overrightarrow {AG} }}\left( B \right) = B' \Rightarrow \overrightarrow {BB'} = \overrightarrow {AG} \\{T_{\overrightarrow {AG} }}\left( C \right) = C' \Rightarrow \overrightarrow {CC'} = \overrightarrow {AG} \end{array} \right.\)
\( + )\)\({T_{\overrightarrow {AG} }}\left( D \right) = A \Rightarrow \overrightarrow {DA} = \overrightarrow {AG} \)
\( \Rightarrow \)\(D,\,\,A,\,\,G\)thẳng hàng.
Và \(A\) là trung điểm của \(DG\).
Câu hỏi 22 :
Cho tam giác đều \(ABE\) và \(BCD\) bằng nhau trên hình bên. Tìm phép tịnh tiến biến ba điểm \(A,\,\,B,\,\,E\) theo thứ tự thành ba điểm \(B,\,\,C,\,\,D\).
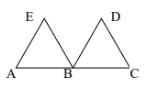
Lời giải chi tiết:
Phép tịnh tiến theo \(\overrightarrow {AB} \) hoặc \(\overrightarrow {BC} \), \(\overrightarrow {ED} \) biến \(A,\,\,B,\,\,E\) theo thứ tự thành 3 điểm \(B,\,\,C,\,\,D\).
Câu hỏi 23 :
Cho lục giác đều \(ABCDEF\) tâm \(O\) (như hình vẽ). Phép tịnh tiến theo véctơ \(\overrightarrow {BC} \) biến hình thoi \(ABOF\) thành hình thoi nào sau đây?
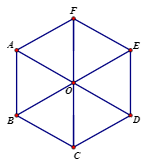
- A \(OBCD\).
- B \(OAFE\).
- C \(ODEF\).
- D \(OCDE\).
Đáp án: D
Phương pháp giải:
Xác định ảnh của từng điểm qua phép tịnh tiến.
Lời giải chi tiết:
\(\begin{array}{l}{T_{\overrightarrow {BC} }}\left( A \right) = O\,\,do\,\,\overrightarrow {AO} = \overrightarrow {BC} \\{T_{\overrightarrow {BC} }}\left( B \right) = C\\{T_{\overrightarrow {BC} }}\left( O \right) = D\,\,do\,\,\overrightarrow {OD} = \overrightarrow {BC} \\{T_{\overrightarrow {BC} }}\left( F \right) = E\,\,do\,\,\overrightarrow {FE} = \overrightarrow {BC} \end{array}\)
Vậy \({T_{\overrightarrow {BC} }}\left( {ABOF} \right) = OCDE\).
Chọn D.
Câu hỏi 24 :
Trong mặt phẳng tọa độ \(Oxy\), phép tịnh tiến theo vectơ \(\overrightarrow v \left( {3; - 2} \right)\) biến đường tròn \(\left( C \right):\,\,{x^2} + {y^2} - 2y = 0\) thành đường tròn \(\left( {C'} \right)\). Tìm tọa độ \(I'\) của đường tròn \(\left( {C'} \right)\).
- A \(I'\left( {3; - 3} \right)\)
- B \(I'\left( { - 3;1} \right)\)
- C \(I'\left( {3; - 1} \right)\)
- D \(I'\left( { - 3;3} \right)\)
Đáp án: C
Phương pháp giải:
Xác định tâm \(I\) của đường tròn \(\left( C \right)\)
Sử dụng biểu thức tọa độ của phép tịnh tiến theo véc tơ \(\overrightarrow v = \left( {a;b} \right)\) biến \(M\left( {x;y} \right)\) thành \(M'\left( {x';y'} \right)\) thì \(\left\{ \begin{array}{l}x' = x + a\\y' = y + b\end{array} \right.\)
Lời giải chi tiết:
Đường tròn \(\left( C \right)\) có tâm \(I\left( {0;1} \right)\)
Ảnh của \(I\left( {0;1} \right)\) qua tịnh tiến theo vectơ \(\overrightarrow v \left( {3; - 2} \right)\) là \(I'\left( {x';y'} \right)\) là tâm của đường tròn \(\left( {C'} \right)\)
Khi đó: \(\left\{ \begin{array}{l}x' = 0 + 3 = 3\\y' = 1 + \left( { - 2} \right) = - 1\end{array} \right. \Rightarrow I'\left( {3; - 1} \right)\)
Chọn C.
Câu hỏi 25 :
Trong hệ trục tọa độ \(Oxy\), cho \(\overrightarrow v \left( {3;3} \right)\) và đường tròn \(\left( C \right):\,\,{\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = 9\). Tìm phương trình đường tròn \(\left( {C'} \right)\) là ảnh của \(\left( C \right)\) qua phép tịnh tiến \({T_{\overrightarrow v }}.\)
- A \((C'):{\left( {x - 4} \right)^2} + {\left( {y - 1} \right)^2} = 9\).
- B \((C'):{\left( {x - 2} \right)^2} + {\left( {y - 5} \right)^2} = 9\)
- C \((C'):{\left( {x + 4} \right)^2} + {\left( {y + 1} \right)^2} = 9\)
- D
\((C'):{\left( {x - 4} \right)^2} + {\left( {y - 1} \right)^2} = 3.\)
Đáp án: A
Phương pháp giải:
Áp dụng tính chất của phép tịnh tiến điểm M thành M’ theo vecto v thì \(\overrightarrow {MM'} = \overrightarrow v \).
Lời giải chi tiết:
Đường tròn (C): \({\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = 9\)có tâm I(1;-2); bán kinh R=3.
Gọi I’ là tâm đường tròn (C’).
Phép tịnh tiến điểm I thành điểm I’ theo véc-tơ \(\overrightarrow v \left( {3;3} \right)\)thì \(\overrightarrow {II'} = \overrightarrow v \)
Suy ra \(I'\left( {4;1} \right)\)
Đường tròn (C’) có tâm là \(I'\left( {4;1} \right)\); R=3 nên có dạng \({\left( {x - 4} \right)^2} + {\left( {y - 1} \right)^2} = 9\)
Chọn A.
Câu hỏi 26 :
Trong mặt phẳng \(Oxy\), cho đường thẳng \(\Delta :\,2x - 3y - 5 = 0\). Ảnh của đường \(\Delta \) qua phép tịnh tiến theo vectơ \(\overrightarrow u = \left( { - 1;2} \right)\) là đường thẳng nào?
- A \(2x - 3y + 13 = 0\)
- B \(2x - 3y - 3 = 0\)
- C \(2x - 3y - 13 = 0\)
- D \(2x - 3y + 3 = 0\)
Đáp án: D
Phương pháp giải:
Sử dụng định nghĩa về phép tịnh tiến trong mặt phẳng.
Lời giải chi tiết:
Gọi \(M\left( {x;y} \right) \in \Delta ;{T_{\overrightarrow u }}\left( M \right) = M'\left( {x';y'} \right) \in \Delta '\)
\( \Rightarrow \left\{ \begin{array}{l}x' = x - 1\\y' = y + 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = x' + 1\\y = y' - 2\end{array} \right. \Rightarrow M\left( {x' + 1;y' - 2} \right) \in d\)
\(M \in d \Rightarrow 2\left( {x' + 1} \right) - 3\left( {y' - 2} \right) - 5 = 0 \Leftrightarrow 2x' - 3y' + 3 = 0\)
Vậy phương trình ảnh của đường thẳng \(\Delta \) là: \(\Delta ' = 2x - 3y + 3 = 0\).
Chọn D.
Câu hỏi 27 :
Cho ba điểm \(A\left( {1;2} \right),\,\,B\left( {2;3} \right),\,\,C\left( {6;7} \right)\). Giả sử qua phép tịnh tiến theo vectơ \(\overrightarrow u \) các điểm \(A,\,\,B,\,\,C\) lần lượt biến thành các điểm \(A'\left( {2;0} \right),\,\,B',\,\,C'\). Khẳng định nào sau đây là đúng?
- A \(B'\left( {3;5} \right)\)
- B \(C'\left( {7;5} \right)\)
- C \(\overrightarrow u \left( {3;2} \right)\)
- D \(\overrightarrow u \left( {1;2} \right)\)
Đáp án: B
Phương pháp giải:
\({T_{\overrightarrow u }}\left( M \right) = M' \Leftrightarrow \overrightarrow {MM'} = \overrightarrow u \).
Lời giải chi tiết:
Ta có \(\overrightarrow {AA'} = \left( {1; - 2} \right)\). Vì \({T_{\overrightarrow u }}\left( A \right) = A' \Leftrightarrow \overrightarrow {AA'} = \overrightarrow u = \left( {1; - 2} \right)\), do đó các đáp án C, D sai.
\(\begin{array}{l}{T_{\overrightarrow u }}\left( B \right) = B' \Leftrightarrow \overrightarrow {BB'} = \overrightarrow u \Rightarrow \left\{ \begin{array}{l}{x_{B'}} - 2 = 1\\{y_{B'}} - 3 = - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_{B'}} = 3\\{y_{B'}} = 1\end{array} \right. \Rightarrow B'\left( {3;1} \right)\\{T_{\overrightarrow u }}\left( C \right) = C' \Leftrightarrow \overrightarrow {CC'} = \overrightarrow u \Rightarrow \left\{ \begin{array}{l}{x_{C'}} - 6 = 1\\{y_{C'}} - 7 = - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_{C'}} = 7\\{y_{C'}} = 5\end{array} \right. \Rightarrow C'\left( {7;5} \right)\end{array}\)
Vậy đáp án B đúng.
Chọn B.
Câu hỏi 28 :
Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có A(1;4), B(4;0), C(-2;-2). Phép tịnh tiến \({T_{\overrightarrow {BC} }}\) biến \(\Delta ABC\) thành \(\Delta A'B'C'\). Tọa độ trực tâm của \(\Delta A'B'C'\) là:
- A (-4;-1)
- B (-1;4)
- C (4;-1)
- D (4;1)
Đáp án: A
Phương pháp giải:
- Sử dụng định nghĩa phép tịnh tiến tìm tọa độ các điểm A’, B’, C’.
- Gọi H(a;b), giải hệ phương trình \(\left\{ \begin{array}{l}\overrightarrow {HA'} .\overrightarrow {B'C'} = 0\\\overrightarrow {HB'} .\overrightarrow {A'C'} = 0\end{array} \right.\) để tìm tọa độ điểm H.
Lời giải chi tiết:
Ta có: \(\overrightarrow {BC} = \left( { - 6; - 2} \right)\).
\(\begin{array}{l}{T_{\overrightarrow {BC} }}\left( A \right) = A'\left( { - 5;2} \right)\\{T_{\overrightarrow {BC} }}\left( B \right) = B' \equiv C \Rightarrow B'\left( { - 2; - 2} \right)\\{T_{\overrightarrow {BC} }}\left( C \right) = C'\left( { - 8; - 4} \right)\end{array}\)
Gọi H(a;b;c) là trực tâm của tam giác A’B’C’, khi đó ta có \(HA' \bot B'C',\,\,HB' \bot A'C'\).
Do đó \(\left\{ \begin{array}{l}\overrightarrow {HA'} .\overrightarrow {B'C'} = 0\\\overrightarrow {HB'} .\overrightarrow {A'C'} = 0\end{array} \right.\).
Ta có:
\(\begin{array}{l}\overrightarrow {HA'} = \left( { - 5 - a;2 - b} \right),\,\,\overrightarrow {B'C'} = \left( { - 6; - 2} \right)\\\overrightarrow {HB'} = \left( { - 2 - a; - 2 - b} \right),\,\,\overrightarrow {A'C'} = \left( { - 3; - 6} \right)\\ \Rightarrow \left\{ \begin{array}{l}\left( { - 5 - a} \right).\left( { - 6} \right) + \left( {2 - b} \right).\left( { - 2} \right) = 0\\\left( { - 2 - a} \right).\left( { - 3} \right) + \left( { - 2 - b} \right).\left( { - 6} \right) = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}30 + 6a - 4 + 2b = 0\\6 + 3a + 12 + 6b = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}6a + 2b = - 26\\3a + 6b = - 18\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - 4\\b = - 1\end{array} \right.\end{array}\)
Vậy \(H\left( { - 4; - 1} \right)\).
Chọn A.
Câu hỏi 29 :
Trong mặt phẳng với hệ tọa độ Oxy. Phép dời hình \(\left\{ \begin{array}{l}x' = x - 3\\y' = y + 1\end{array} \right.\) biến parabol \(\left( P \right):\,\,y = {x^2} + 1\) thành parabol \(\left( {P'} \right)\) có phương trình là:
- A \(y = - {x^2} - 6x + 5\)
- B \(y = - {x^2} + 6x - 5\)
- C \(y = {x^2} + 6x + 11\)
- D \(y = - {x^2} - 6x - 7\)
Đáp án: C
Phương pháp giải:
- Gọi \(M\left( {x;y} \right) \in \left( P \right)\) và \(M'\left( {x';y'} \right) = F\left( M \right)\). Biểu diễn \(x\) và \(y\) theo x’ và y’.
- Thay tọa độ điểm M theo x’ và y’ vào phương trình (P), tìm ra mối liên hệ giữa x’ và y’.
- Kết luận ảnh của (P) qua phép dời hình.
Lời giải chi tiết:
Gọi \(M\left( {x;y} \right) \in \left( P \right)\) và \(M'\left( {x';y'} \right) = F\left( M \right)\) \( \Rightarrow \left\{ \begin{array}{l}x' = x - 3\\y' = y + 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = x' + 3\\y = y' - 1\end{array} \right.\).
\( \Rightarrow M\left( {x' + 3;y' - 1} \right)\).
Vì \(M \in \left( P \right) \Rightarrow y' - 1 = {\left( {x' + 3} \right)^2} + 1\)
\(\begin{array}{l} \Leftrightarrow y' = x{'^2} + 6x' + 9 + 1 + 1\\ \Leftrightarrow y' = x{'^2} + 6x' + 11\end{array}\)
Do đó điểm \(M'\) thuộc \(\left( {P'} \right):\,\,y = {x^2} + 6x + 11\).
Vậy phép dời hình đã cho biến \(\left( P \right):\,\,y = {x^2} + 1\) thành \(\left( {P'} \right):\,\,y = {x^2} + 6x + 11\).
Chọn C.
Câu hỏi 30 :
Trong mặt phẳng với hệ tọa độ \(Oxy\), cho đường thẳng \(\Delta \) có phương trình \(5x-y+1=0\). Thực hiện phép tịnh tiến theo phương của trục hoành về phía trái 2 đơn vị, sau đó tiếp tục thực hiện phép tịnh tiến theo phương của trục tung về phía trên 3 đơn vị, đường thẳng \(\Delta \) biến thành đường thẳng \(\Delta '\) có phương trình là:
- A \(5x-y+14=0\)
- B \(5x-y-7=0\)
- C \(5x - y + 5 = 0\)
- D \(5x-y-12=0\)
Đáp án: A
Phương pháp giải:
- Xác định tọa độ vectơ tịnh tiến.
- Sử dụng biểu thức tọa độ của phép tịnh tiến.
\({{T}_{\overrightarrow{v}}}\left( M \right)=M'\) với \(M\left( x;y \right);\,\,M'\left( x';y' \right);\,\,\overrightarrow{v}\left( a;b \right)\) thì \(\left\{ \begin{align}x'=x+a \\ y'=y+b \\ \end{align} \right.\).
Lời giải chi tiết:
Từ giả thiết suy ra \(\Delta '\) là ảnh của \(\Delta \) qua phép tịnh tiến theo vectơ \(\overrightarrow{u}=\left( -2;3 \right)\).
Gọi \(M\left( {x;y} \right) \in \Delta \);
\({T_{\overrightarrow u }}\left( M \right) = M'\left( {x';y'} \right) \Rightarrow \left\{ \begin{array}{l}
x' = x - 2\\
y' = y + 3
\end{array} \right. \Rightarrow \left\{ \begin{array}{l}
x = x' + 2\\
y = y' - 3
\end{array} \right.\)
\(\Rightarrow M\left( x'+2;y'-3 \right)\in \left( \Delta \right)\Rightarrow \) Thay tọa độ điểm \(M\) vào phương trình \(\Delta \) ta có:
\(5\left( {x' + 2} \right) - \left( {y' - 3} \right) + 1 = 0 \Leftrightarrow 5x' - y' + 14 = 0\)
Chứng tỏ \(M'\in \left( \Delta ' \right):\,\,5x-y+14=0\).
Vậy phép tịnh tiến theo \(\overrightarrow{u}=\left( -2;3 \right)\) biến \(\Delta :\,\,5x-y+1=0\) thành đường thẳng \(\Delta ':\,\,5x - y + 14 = 0\).
Chọn A.
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
 |
 |
 |
 |
 |
 |
 |
 |