30 bài tập trắc nghiệm hàm số lượng giác mức độ nhận biết, thông hiểu
Làm đề thiCâu hỏi 1 :
Tập xác định của hàm số \(y = \sqrt {{{1 + \cos x} \over {{{\sin }^2}x}}}\) là:
- A \(R\backslash \left\{ {{\pi \over 3} + k\pi \,\,\left( {k \in Z} \right)} \right\}\)
- B \(R\backslash \left\{ {k\pi \,\,\left( {k \in Z} \right)} \right\}\)
- C R
- D \(R\backslash \left\{ {\pi + k2\pi \,\,\left( {k \in Z} \right)} \right\}\)
Đáp án: B
Phương pháp giải:
+) \(\sqrt A \) xác định \( \Leftrightarrow A \ge 0\).
+) \(\dfrac{1}{B}\) xác định \( \Leftrightarrow B \ne 0\).
Lời giải chi tiết:
Ta có:
\(\eqalign{ & - 1 \le \cos x \le 1 \Rightarrow 1 + \cos x \ge 0\, \cr & {\sin ^2}x \ge 0 \cr} \)
Do đó hàm số xác định khi và chỉ khi \(\sin x \ne 0 \Leftrightarrow x \ne k\pi \,\,\left( {k \in Z} \right)\)
Vậy tập xác định của hàm số là \(R\backslash \left\{ {k\pi \,\,\left( {k \in Z} \right)} \right\}\)
Chọn B.
Câu hỏi 2 :
Hàm số nào sau đây là hàm số chẵn:
- A \(y = \sin 2x\)
- B \(y = x\cos x\)
- C \(y = \cos x\cot x\)
- D \(y = {{\tan x} \over {\sin x}}\)
Đáp án: D
Phương pháp giải:
Cho hàm số \(y = f\left( x \right)\) có TXĐ là \(D\).
+) Nếu \(\forall x \in D \Rightarrow - x \in D\) và \(f\left( { - x} \right) = f\left( x \right) \Rightarrow y = f\left( x \right)\) là hàm số chẵn.
+) Nếu \(\forall x \in D \Rightarrow - x \in D\) và \(f\left( { - x} \right) = - f\left( x \right) \Rightarrow y = f\left( x \right)\) là hàm số lẻ.
Lời giải chi tiết:
Với đáp án A ta có:
TXĐ: \(D = R\) ; \(x \in D \Rightarrow - x \in D\)
Ta có: \(y = f\left( x \right) = \sin 2x \Rightarrow f\left( { - x} \right) = \sin \left( { - 2x} \right) = - \sin 2x = - f\left( x \right)\)
Vậy hàm số \(y = \sin 2x\) là hàm lẻ.
Với đáp án B ta có:
TXĐ:\(D = R\) ; \(x \in D \Rightarrow - x \in D\)
Ta có:
\(\eqalign{ & y = f\left( x \right) = x\cos x \cr & \Rightarrow f\left( { - x} \right) = - x.\cos \left( { - x} \right) = - x.\cos x = - f\left( x \right) \cr} \)
Vậy hàm số \(y = x\cos x\) là hàm lẻ.
Với đáp án C ta có:
TXĐ: \(D = R\backslash \left\{ {k\pi \,\,\left( {k \in Z} \right)} \right\}\,\,;x \in D \Rightarrow - x \in D\)
Ta có:
\(\eqalign{ & y = f\left( x \right) = \cos x\cot x \cr & \Rightarrow f\left( { - x} \right) = cox\left( { - x} \right)\cot \left( { - x} \right) = \cos x\left( { - {\mathop{\rm cotx}\nolimits} } \right) = - \cos x.\cot x = - f\left( x \right) \cr} \)
Vậy hàm số \(y = \cos x\cot x\) là hàm lẻ.
Với đáp án D ta có: \(y = {{\tan x} \over {\sin x}} = {1 \over {\cos x}}\)
TXĐ: \(D = R\backslash \left\{ {{{k\pi } \over 2}\,\,\left( {k \in Z} \right)} \right\}\,\,;x \in D \Rightarrow - x \in D\)
Ta có: \(y = f\left( x \right) = {1 \over {\cos x}} \Rightarrow f\left( { - x} \right) = {1 \over {\cos \left( { - x} \right)}} = {1 \over {\cos x}} = f\left( x \right)\)
Vậy hàm số \(y = {{\tan x} \over {\sin x}}\) là hàm chẵn.
Chọn D.
Câu hỏi 3 :
Tập xác định của hàm số \(y = \cot \left( {2x - {\pi \over 3}} \right)\) là:
- A \(R\backslash \left\{ {{\pi \over 6} + {{k\pi } \over 2}\,\,\left( {k \in Z} \right)} \right\}\)
- B \(R\backslash \left\{ {{\pi \over 6} + k\pi \,\,\left( {k \in Z} \right)} \right\}\)
- C \(R\backslash \left\{ {{{5\pi } \over 6} + k\pi \,\,\left( {k \in Z} \right)} \right\}\)
- D Kết quả khác
Đáp án: A
Phương pháp giải:
Hàm số \(y = \cot x\) xác định \( \Leftrightarrow x \ne k\pi \).
Lời giải chi tiết:
\(y = \cot \left( {2x - {\pi \over 3}} \right) = {{\cos \left( {2x - {\pi \over 3}} \right)} \over {\sin \left( {2x - {\pi \over 3}} \right)}}\)
Hàm số xác định khi và chỉ khi \(\sin \left( {2x - {\pi \over 3}} \right) \ne 0 \Leftrightarrow 2x - {\pi \over 3} \ne k\pi \Leftrightarrow 2x \ne {\pi \over 3} + k\pi \Leftrightarrow x \ne {\pi \over 6} + {{k\pi } \over 2}\,\,\left( {k \in Z} \right)\)
Vậy tập xác định của hàm số là \(R\backslash \left\{ {{\pi \over 6} + {{k\pi } \over 2}\,\,\left( {k \in Z} \right)} \right\}\)
Chọn A.
Câu hỏi 4 :
Hàm số \(y = 1 - {\sin ^2}x\) là:
- A Hàm số lẻ
- B Hàm số không tuần hoàn
- C Hàm số chẵn
- D Hàm số không chẵn không lẻ.
Đáp án: C
Phương pháp giải:
Cho hàm số \(y = f\left( x \right)\) có TXĐ là \(D\).
+) Nếu \(\forall x \in D \Rightarrow - x \in D\) và \(f\left( { - x} \right) = f\left( x \right) \Rightarrow y = f\left( x \right)\) là hàm số chẵn.
+) Nếu \(\forall x \in D \Rightarrow - x \in D\) và \(f\left( { - x} \right) = - f\left( x \right) \Rightarrow y = f\left( x \right)\) là hàm số lẻ.
Lời giải chi tiết:
Ta có:\(y = f\left( x \right) = 1 - {\sin ^2}x = {\cos ^2}x\)
\( \Rightarrow f\left( { - x} \right) = {\cos ^2}\left( { - x} \right) = {\cos ^2}x = f\left( x \right)\) . Do đó hàm số là hàm chẵn.
Chọn C.
Câu hỏi 5 :
Giá trị lớn nhất của hàm số \(y = {2 \over {1 + {{\tan }^2}x}}\) là:
- A Không xác định
- B 2
- C 1
- D \( 3 \over 2 \)
Đáp án: B
Lời giải chi tiết:
Hướng dẫn giải chi tiết
TXĐ: \(D = R\backslash \left\{ {{\pi \over 2} + k\pi \,\,\left( {k \in Z} \right)} \right\}\)
Ta có: \({\tan ^2}x \ge 0 \Leftrightarrow 1 + {\tan ^2}x \ge 1 \Leftrightarrow {2 \over {1 + {{\tan }^2}x}} \le 2\)
Vậy \(\max y = 2 \Leftrightarrow \tan x = 0 \Leftrightarrow x = k\pi \,\,\left( {k \in Z} \right)\)
Chọn B.
Câu hỏi 6 :
Hàm số \(y = \left| {\sin x} \right|\) xét trên \(\left[ { - {\pi \over 2};{\pi \over 2}} \right]\)
- A Không có GTLN
- B GTNN là -1
- C GTLN là 1
- D GTNN là 1
Đáp án: C
Phương pháp giải:
Tập giá trị của hàm sin là: \( - 1 \le \sin x \le 1\).
Lời giải chi tiết:
TXĐ: \(D=R\)
Ta lập bảng giá trị của hàm số trên đoạn \(\left[ { - {\pi \over 2};{\pi \over 2}} \right]\)

Ta thấy với \(x \in \left[ { - {\pi \over 2};{\pi \over 2}} \right] \Rightarrow - 1 \le \sin x \le 1 \Rightarrow 0 \le \left| {\sin x} \right| \le 1\)
Vậy \(\mathop {min}\limits_{x \in \left[ { - {\pi \over 2};{\pi \over 2}} \right]} y = 0\,\,;\mathop {max}\limits_{x \in \left[ { - {\pi \over 2};{\pi \over 2}} \right]} y = 1\)
Chọn C.
Câu hỏi 7 :
Hàm số \(y = {\cos ^2}3x\) là hàm số tuần hoàn với chu kì:
- A \( 3 \pi \)
- B \( \pi \)
- C \( \pi \over 3 \)
- D \(3 \pi \over 2 \)
Đáp án: C
Phương pháp giải:
Hàm số \(\cos kx\) tuần hoàn với chu kì \(\dfrac{{2\pi }}{k}\).
Lời giải chi tiết:
Ta có: \(y = {\cos ^2}3x = {{1 + \cos 6x} \over 2}\)
Hàm số \(y = \cos x\) tuần hoàn với chu kì \( 2 \pi \) suy ra hàm số tuần hoàn với chu kì \({{2\pi } \over 6} = {\pi \over 3}\)
Vậy hàm số \(y = {\cos ^2}3x\) tuần hoàn với chu kì \( \pi \over 3\)
Chọn C.
Câu hỏi 8 :
Hàm số \(y = \sin {x \over 2} + \sin {x \over 3}\) là hàm số tuần hoàn với chu kì:
- A \( 2 \pi \)
- B \( 6 \pi \)
- C \( 9 \pi \)
- D \( 12 \pi \)
Đáp án: D
Phương pháp giải:
Hàm số \(\sin kx\) tuần hoàn với chu kì \(\dfrac{{2\pi }}{k}\).
Lời giải chi tiết:
Hàm số \( y= \sin x \) là hàm số tuần hoàn với chu kì \( 2 \pi \)
Suy ra hàm số \( y= \sin {x \over 2} \) là hàm số tuần hoàn với chu kì \(2.2 \pi = 4 \pi \)
Và hàm số \( y= \sin {x \over 3} \) tuần hoàn với chu kì \(3.2 \pi = 6 \pi \)
Vậy hàm số \(y = \sin {x \over 2} + \sin {x \over 3}\) là hàm số tuần hoàn với chu kì \( 12 \pi \)
Chọn D.
Câu hỏi 9 :
Hàm số \(y = 2{\sin ^2}x + 3{\cos ^2}3x\) là hàm số tuần hoàn với chu kì:
- A \( \pi \)
- B \(2 \pi \)
- C \(3 \pi \)
- D \( \pi \over 3 \)
Đáp án: A
Phương pháp giải:
Sử dụng công thức biến đổi tích thành tổng.
Lời giải chi tiết:
\(\eqalign{
& y = 2{\sin ^2}x + 3{\cos ^2}3x = 2.{{1 - \cos 2x} \over 2} + 3.{{1 + \cos 6x} \over 2} \cr
& \,\,\,\, = 1 - \cos 2x + {3 \over 2} + {3 \over 2}\cos 6x = {3 \over 2}\cos 6x - \cos 2x + {5 \over 2} \cr} \)
Hàm số \( y= \cos x\) là hàm số tuần hoàn với chu kì \(2 \pi \)
Suy ra hàm số \( y= \cos 2x\) là hàm số tuần hoàn với chu kì \({{2\pi } \over 2} = \pi \)
Hàm số \( y= \cos 6x\) là hàm số tuần hoàn với chu kì \({{2\pi } \over 6} = {\pi \over 3}\)
Vậy hàm số \(y = 2{\sin ^2}x + 3{\cos ^2}3x\) là hàm số tuần hoàn với chu kì \( \pi \)
Chọn A.
Câu hỏi 10 :
Hàm số \(y = \sin 5x\sin 2x\) là hàm số tuần hoàn với chu kì:
- A \(2 \pi \)
- B \({{2\pi } \over 3}\)
- C \({{2\pi } \over 7}\)
- D \({{7\pi } \over 3}\)
Đáp án: A
Phương pháp giải:
Sử dụng công thức biến đổi tích thành tổng.
Lời giải chi tiết:
\(y = \sin 5x\sin 2x = - {1 \over 2}\left( {\cos 7x - \cos 3x} \right)\)
Hàm số \( y= \cos x\) là hàm số tuần hoàn với chu kì \(2 \pi \)
Suy ra hàm số \( y= \cos 7x\) là hàm số tuần hoàn với chu kì \({{2\pi } \over 7}\)
Hàm số \(y = \cos 3x\) là hàm số tuần hoàn với chu kì \({{2\pi } \over 3}\)
Vậy hàm số \(y = \sin 5x\sin 2x\) là hàm số tuần hoàn với chu kì \(2 \pi \)
Chọn A.
Câu hỏi 11 :
Trong bốn hàm số: \((1){\text{ }}y = \sin 2x;{\text{ }}(2){\text{ }}y = \cos 4x;{\text{ (3) }}y = \tan 2x;{\text{ }}(4){\text{ }}y = \cot 3x\) có mấy hàm số tuần hoàn với chu kỳ \(\dfrac{\pi }{2}\)?
- A \(0\)
- B \(2\)
- C \(3\)
- D \(1\)
Đáp án: B
Lời giải chi tiết:
Phương pháp: Hàm số \(y = \sin kx \) và \(y = \cos kx\) tuần hoàn với chu kỳ \(\dfrac{{2\pi }}{k}\), hàm số \(y = \tan kx\) và \(y = \cot kx\) tuần hoàn với chu kỳ \(\dfrac{\pi }{k}\)
Trong các hàm số đã cho, hàm số \(y = \cos4x\) và \(y = \tan2x\) tuần hoàn với chu kỳ \(\dfrac{\pi }{2}\)
Chọn đáp án B
Câu hỏi 12 :
Tập xác định D của hàm số \(y=\frac{\tan x-1}{\sin x}\) là:
- A \(D=\mathbb{R}\backslash \left\{ \frac{\pi }{2}+k\pi |k\in \mathbb{Z} \right\}.\)
- B \(D=\mathbb{R}\backslash \left\{ k\pi |k\in \mathbb{Z} \right\}.\)
- C \(D=\mathbb{R}\backslash \left\{ 0 \right\}.\)
- D \(D=\mathbb{R}\backslash \left\{ \frac{k\pi }{2}|k\in \mathbb{Z} \right\}.\)
Đáp án: D
Lời giải chi tiết:
Phương pháp:
Tìm điều kiện xác định của hàm số:
- \(\frac{P\left( x \right)}{Q\left( x \right)}\) xác định nếu \(Q\left( x \right)\ne 0\).
- \(\sqrt{P\left( x \right)}\) xác định nếu \(P\left( x \right)\ge 0\).
- \(\tan u\left( x \right)\) xác định nếu \(u\left( x \right)\ne k\pi \) , \(\cot u\left( x \right)\) xác định nếu \(x\ne \frac{\pi }{2}+k\pi \).
Cách giải:
Hàm số \(y=\frac{\tan x-1}{\sin x}\) xác định khi: \(\left\{ \begin{matrix}\cos x\ne 0 \\\sin x\ne 0 \\\end{matrix} \right.\Leftrightarrow \left\{ \begin{matrix} x\ne k\pi \\x\ne \frac{\pi }{2}+k\pi \\\end{matrix} \right.\Leftrightarrow x\ne \frac{k\pi }{2}\).
Vậy TXĐ của hàm số là \(D=R\backslash \left\{ \frac{k\pi }{2},k\in Z \right\}\).
Chọn D.
Câu hỏi 13 :
Trong các hàm số sau đây, hàm số nào là hàm số tuần hoàn?
- A \(y=\sin 2x.\)
- B \(y=2\left( \sin x\cos x-x \right)-{{x}^{2}}-\sin 2x.\)
- C \(y=\frac{x-1}{x+1}.\)
- D \(y={{x}^{3}}-3x+2.\)
Đáp án: A
Lời giải chi tiết:
Phương pháp:
Hàm số \(y=f\left( x \right)\) được gọi là tuần hoàn theo chu kì T\(\Leftrightarrow f\left( x \right)=f\left( x+T \right)\).
Cách giải
Hàm số \(y=\sin 2x\) tuần hoàn với chu kì \(\pi \) và \(\sin \left( 2\left( x+\pi \right) \right)=\sin \left( 2x+2\pi \right)=\sin 2x\)
Chọn A.
Câu hỏi 14 :
Tìm tập xác định \(D\) của hàm số \(y=\tan 2x.\)
- A \(D=\mathbb{R}\backslash \left\{ \frac{\pi }{4}+k2\pi |k\in \mathbb{Z} \right\}.\)
- B \(D=\mathbb{R}\backslash \left\{ \frac{\pi }{2}+k\pi |k\in \mathbb{Z} \right\}.\)
- C \(D=\mathbb{R}\backslash \left\{ \frac{\pi }{4}+k\pi |k\in \mathbb{Z} \right\}.\)
- D \(D=\mathbb{R}\backslash \left\{ \frac{\pi }{4}+\frac{k\pi }{2}|k\in \mathbb{Z} \right\}.\)
Đáp án: D
Phương pháp giải:
Phương pháp. Sử dụng công thức cơ bản của lượng giác.
Lời giải chi tiết:
Lời giải chi tiết.
Tập xác định
\(c{\rm{os2x}} \ne {\rm{0}} \Leftrightarrow {\rm{2x}} \ne \frac{\pi }{2} + k\pi \Leftrightarrow x \ne \frac{\pi }{4} + \frac{{k\pi }}{2}\,\left( {k \in Z} \right).\)
Chọn đáp án D.
Câu hỏi 15 :
Chọn phát biểu đúng.
- A Các hàm số \(y=\sin x,y=\cos x,y=\cot x\) đều là hàm số chẵn.
- B Các hàm số \(y=\sin x,y=\cos x,y=\cot x\) đều là hàm số lẻ.
- C Các hàm số \(y=\sin x,y=\cot x,y=\tan x\) đều là hàm số chẵn.
- D Các hàm số \(y=\sin x,y=\cot x,y=\tan x\) đều là hàm số lẻ.
Đáp án: D
Phương pháp giải:
Phương pháp. Dùng định nghĩa hàm chẵn lẻ, và tính chất của các hàm lượng giác.
Lời giải chi tiết:
Lời giải chi tiết.
Hàm số \(y=\sin x\) là hàm số lẻ nên ta loại đáp án \(A,C.\)
Hàm số \(y=\cos x\) là hàm số chẵn nên ta loại tiếp đáp án B.
Đáp án D đúng.
Chọn đáp án D.
Câu hỏi 16 :
Khẳng định nào dưới đây là sai ?
- A Hàm số \(y = \sin x\) là hàm số lẻ
- B Hàm số \(y = \tan x\) là hàm số lẻ
- C Hàm số \(y = \cos x\) là hàm số lẻ
- D Hàm số \(y = \cot x\) là hàm số lẻ
Đáp án: C
Phương pháp giải:
Phương pháp: Hàm số \(y = f\left( x \right)\) là hàm số lẻ \( \Leftrightarrow f\left( {-x} \right) = -f\left( x \right)\) với mọi \(x \in D\)
Lời giải chi tiết:
Cách giải: Vì \(\sin \left( {-x} \right) = -\sin x,\cos \left( {-x} \right) = \cos x,\tan \left( {-x} \right) = -\tan x,\cot \left( {-x} \right) = -\cot \left( x \right)\) nên chỉ có \(3\) hàm số \(y = \sin x;y = \tan x\) và \(y = \cot x\) là các hàm số lẻ.
Chọn đáp án C
Câu hỏi 17 :
Tập xác định của hàm số \(y=2\sin \sqrt{\frac{1-x}{1+x}}+3\cos x\) là:
- A \(\left( -1;1 \right)\)
- B \(\left( -1;1 \right]\)
- C \(\left[ -1;1 \right]\)
- D R
Đáp án: B
Phương pháp giải:
Tìm TXĐ của hàm số:
\(\frac{A}{B}\) xác định \(\Leftrightarrow B\ne 0\).
\(\sqrt{A}\) xác định \(\Leftrightarrow A\ge 0\)
\(\tan x=\frac{\sin x}{\cos x}\) xác định \(\Leftrightarrow \cos x\ne 0\Leftrightarrow x\ne \frac{\pi }{2}+k\pi \,\,\left( k\in Z \right)\)
\(\cot x=\frac{\cos x}{\sin x}\) xác định \(\Leftrightarrow \sin x\ne 0\Leftrightarrow x\ne k\pi \,\,\left( k\in Z \right)\)
Lời giải chi tiết:
Hàm số \(y = 2\sin \sqrt {\frac{{1 - x}}{{1 + x}}} + 3\cos x\) xác định \( \Leftrightarrow \left\{ \begin{array}{l}\frac{{1 - x}}{{1 + x}} \ge 0\\1 + x \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 1 < x \le 1\\x \ne - 1\end{array} \right. \Rightarrow - 1 < x \le 1\)
Vậy tập xác định của hàm số là \(D=\left( -1;1 \right]\).
Câu hỏi 18 :
Tập xác định của hàm số \(y=\frac{x-1}{\cos \left( x+\pi \right)}\) là:
- A \(D=R\backslash \left\{ \frac{\pi }{4}+\frac{k\pi }{2} \right\}\)
- B \(D=R\backslash \left\{ \frac{\pi }{2}+k\pi \right\}\)
- C \(D=R\backslash \left\{ \frac{k\pi }{2} \right\}\)
- D \(D=R\backslash \left\{ \frac{k\pi }{4} \right\}\)
Đáp án: B
Phương pháp giải:
Tìm TXĐ của hàm số:
\(\frac{A}{B}\) xác định \(\Leftrightarrow B\ne 0\).
\(\sqrt{A}\) xác định \(\Leftrightarrow A\ge 0\)
\(\tan x=\frac{\sin x}{\cos x}\) xác định \(\Leftrightarrow \cos x\ne 0\Leftrightarrow x\ne \frac{\pi }{2}+k\pi \,\,\left( k\in Z \right)\)
\(\cot x=\frac{\cos x}{\sin x}\) xác định \(\Leftrightarrow \sin x\ne 0\Leftrightarrow x\ne k\pi \,\,\left( k\in Z \right)\)
Lời giải chi tiết:
Hàm số \(y=\frac{x-1}{\cos \left( x+\pi \right)}\) xác định khi và chỉ khi \
\(\begin{array}{l}
\cos \left( {x + \pi } \right) \ne 0 \Leftrightarrow x + \pi \ne \dfrac{\pi }{2} + k\pi \\
\Leftrightarrow x \ne - \dfrac{\pi }{2} + k\pi \Leftrightarrow x \ne \dfrac{\pi }{2} + k\pi \,\,\left( {k \in Z} \right)
\end{array}\)
Chọn B.
Câu hỏi 19 :
Tìm tập xác định của hàm số \(y=\cos 2x+5\):
- A \(R\backslash \left\{ \frac{\pi }{4}+\frac{k\pi }{2} \right\}\)
- B \(R\backslash \left\{ \frac{\pi }{2}+k\pi \right\}\)
- C R
- D \(R\backslash \left\{ 5 \right\}\)
Đáp án: C
Phương pháp giải:
Tìm TXĐ của hàm số:
\(\frac{A}{B}\) xác định \(\Leftrightarrow B\ne 0\).
\(\sqrt{A}\) xác định \(\Leftrightarrow A\ge 0\)
\(\tan x=\frac{\sin x}{\cos x}\) xác định \(\Leftrightarrow \cos x\ne 0\Leftrightarrow x\ne \frac{\pi }{2}+k\pi \,\,\left( k\in Z \right)\)
\(\cot x=\frac{\cos x}{\sin x}\) xác định \(\Leftrightarrow \sin x\ne 0\Leftrightarrow x\ne k\pi \,\,\left( k\in Z \right)\)
Lời giải chi tiết:
Hàm số \(y=\cos 2x+5\) xác định \(\forall x\in R\Rightarrow D=R.\)
Chọn C.
Câu hỏi 20 :
Tìm tập xác định của hàm số \(y=\tan 2x+\cot 2x\):
- A \(R\backslash \left\{ \frac{\pi }{4}+\frac{k\pi }{2} \right\}\)
- B R
- C \(R\backslash \left\{ \frac{k\pi }{2} \right\}\)
- D \(R\backslash \left\{ \frac{k\pi }{4} \right\}\)
Đáp án: D
Phương pháp giải:
Tìm TXĐ của hàm số:
\(\frac{A}{B}\) xác định \(\Leftrightarrow B\ne 0\).
\(\sqrt{A}\) xác định \(\Leftrightarrow A\ge 0\)
\(\tan x=\frac{\sin x}{\cos x}\) xác định \(\Leftrightarrow \cos x\ne 0\Leftrightarrow x\ne \frac{\pi }{2}+k\pi \,\,\left( k\in Z \right)\)
\(\cot x=\frac{\cos x}{\sin x}\) xác định \(\Leftrightarrow \sin x\ne 0\Leftrightarrow x\ne k\pi \,\,\left( k\in Z \right)\)
Lời giải chi tiết:
Hàm số \(y=\tan 2x+\cot 2x\) xác định \( \Leftrightarrow \left\{ \begin{array}{l}\cos 2x \ne 0\\sin2x \ne 0\end{array} \right. \Leftrightarrow \sin 4x \ne 0 \Leftrightarrow 4x \ne k\pi \Leftrightarrow x \ne \frac{{k\pi }}{4}\,\,\left( {k \in Z} \right)\).
Vậy TXĐ: \(D=R\backslash \left\{ \frac{k\pi }{4} \right\}\)
Chọn D.
Câu hỏi 21 :
GTLN, GTNN của hàm số \(y=2-\cos x\)là:
- A 2; - 2
- B 2; 1
- C 3; 1
- D 3; -1
Đáp án: C
Phương pháp giải:
Tập giá trị của hàm số \(y=\sin x,y=\cos x\)là: \(-1\le \sin x\le 1\,\,;\,\,-1\le \cos x\le 1\)
Lời giải chi tiết:
Ta có: \(-1\le \cos x\le 1\Leftrightarrow -1\le -\cos x\le 1\Leftrightarrow 1\le 2-\cos x\le 3.\)
Vậy \(\max y=3,\min y=1.\)
Chọn C.
Câu hỏi 22 :
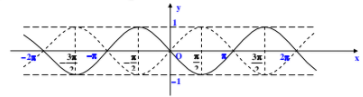
Trong hình sau thì đường nét liền và nét đứt lần lượt là đồ thị của các hàm số nào:
- A \(y=\sin x,y=-\sin x\)
- B \(y=-\sin x,y=\sin x\)
- C \(y=\cos x,y=-\cos x\)
- D \(y=-\cos x,y=\cos x\)
Đáp án: B
Phương pháp giải:
- Đồ thị hàm số \(y=\sin x\)đồng biến trên \(\left( 0;\frac{\pi }{2} \right)\)
- Đồ thị hàm số \(y=\cos x\)nghịch biến trên \(\left( 0;\frac{\pi }{2} \right)\)
Lời giải chi tiết:
Xét cả hai đồ thị hàm số đều đi qua điểm O(0; 0) nên loại C và D.
Xét đường nét liền trên \(\left( 0;\frac{\pi }{2} \right)\) ta thấy đồ thị hàm số nghịch biến nên đường nét liền là đồ thị hàm số \(y=-\sin x\)
Xét đường nét liền trên \(\left( 0;\frac{\pi }{2} \right)\) ta thấy đồ thị hàm số đồng biến nên đường nét liền là đồ thị hàm số \(y=\sin x\).
Chọn B.
Câu hỏi 23 :
Điều kiện xác định của hàm số \(y=\frac{2\sin x+1}{1-\cos x}\) là:
- A \(x\ne \frac{\pi }{2}+k\pi \)
- B \(x\ne k2\pi \)
- C \(x\ne \frac{\pi }{2}+k2\pi \)
- D \(x\ne k\pi \)
Đáp án: B
Phương pháp giải:
Tìm TXĐ của hàm số:
\(\frac{A}{B}\) xác định \(\Leftrightarrow B\ne 0\).
\(\sqrt{A}\) xác định \(\Leftrightarrow A\ge 0\)
\(\tan x=\frac{\sin x}{\cos x}\) xác định \(\Leftrightarrow \cos x\ne 0\Leftrightarrow x\ne \frac{\pi }{2}+k\pi \,\,\left( k\in Z \right)\)
\(\cot x=\frac{\cos x}{\sin x}\) xác định \(\Leftrightarrow \sin x\ne 0\Leftrightarrow x\ne k\pi \,\,\left( k\in Z \right)\)
Lời giải chi tiết:
Hàm số xác định khi và chỉ khi \(1-\cos x\ne 0\Leftrightarrow \cos x\ne 1\Leftrightarrow x\ne k2\pi \,\,\left( k\in Z \right).\)
Chọn B.
Câu hỏi 24 :
Tập giá trị của hàm số \(y=\cos 2x+4{{\sin }^{2}}x-2\) là:
- A \(\left[ -2;3 \right]\)
- B \(\left[ -1;1 \right]\)
- C \(\left[ -2;2 \right]\)
- D \(\left[ -1;3 \right]\)
Đáp án: B
Phương pháp giải:
Tập giá trị của hàm số \(y=\sin x,y=\cos x\)là: \(-1\le \sin x\le 1\,\,;\,\,-1\le \cos x\le 1\)
Lời giải chi tiết:
\(\begin{array}{l}y = \cos 2x + 4{\sin ^2}x - 2\\y = 1 - 2{\sin ^2}x + 4{\sin ^2}x - 2\\y = 2{\sin ^2}x - 1\end{array}\)
Ta có: \(0\le {{\sin }^{2}}x\le 1\Leftrightarrow 0\le 2{{\sin }^{2}}x\le 2\Leftrightarrow -1\le 2{{\sin }^{2}}x-1\le 1\Leftrightarrow -1\le y\le 1.\)
Vậy tập giá tri của hàm số là \(\left[ -1;1 \right]\).
Chọn B.
Câu hỏi 25 :
Chọn phát biểu sai?
- A Các hàm số \(y=\sin x,y=\cos x\) tuần hoàn với chu kì \(2\pi \)
- B Các hàm số \(y=\tan x,y=\cot x\) tuần hoàn với chu kì \(\pi \)
- C Hàm số \(y=\sin x\) đồng biến trên \(\left( 0;\pi \right)\)
- D Hàm số \(y=\cos x\) nghịch biến trên \(\left( 0;\pi \right)\).
Đáp án: C
Phương pháp giải:
Sử dụng các kiến thức liên quan đến sự tuần hoàn của hàm số lượng giác,tính đồng biến nghịch biến của các hàm số lượng giác.
Lời giải chi tiết:
Dễ thấy A và B đúng.
Trên \(\left( 0;\pi \right)\) hàm số y = cos x nghịch biến, hàm số \(y=\sin x\) đồng biến trên \(\left( 0;\frac{\pi }{2} \right)\) và nghịch biến trên \(\left( \frac{\pi }{2};\pi \right)\).
Chọn C.
Câu hỏi 26 :
Tập xác định của hàm số \(y=\cos \sqrt{2x-4}+2x+3\) là:
- A \(D=\left[ 2;+\infty \right)\)
- B \(D=\left( 2;+\infty \right)\)
- C \(D=\left( -\infty ;2 \right)\)
- D D = R.
Đáp án: A
Phương pháp giải:
Tìm TXĐ của hàm số:
\(\frac{A}{B}\) xác định \(\Leftrightarrow B\ne 0\).
\(\sqrt{A}\) xác định \(\Leftrightarrow A\ge 0\)
\(\tan x=\frac{\sin x}{\cos x}\) xác định \(\Leftrightarrow \cos x\ne 0\Leftrightarrow x\ne \frac{\pi }{2}+k\pi \,\,\left( k\in Z \right)\)
\(\cot x=\frac{\cos x}{\sin x}\) xác định \(\Leftrightarrow \sin x\ne 0\Leftrightarrow x\ne k\pi \,\,\left( k\in Z \right)\)
Lời giải chi tiết:
Hàm số xác định \(\Leftrightarrow 2x-4\ge 0\Leftrightarrow x\ge 2.\)
Vậy tập xác định của hàm số là \(D=\left[ 2;+\infty \right).\)
Chọn A.
Câu hỏi 27 :
Đồ thị hàm số \(y=\tan x-2\) đi qua:
- A \(O\left( 0;0 \right)\)
- B \(M\left( \frac{\pi }{4};-1 \right)\)
- C \(N\left( 1;\frac{\pi }{4} \right)\)
- D \(P\left( -\frac{\pi }{4};1 \right)\)
Đáp án: B
Phương pháp giải:
Điểm \(M\left( {{x}_{0}},{{y}_{0}} \right)\) được gọi là thuộc đồ thị hàm số \(y=f\left( x \right)\Leftrightarrow {{y}_{0}}=f\left( {{x}_{0}} \right).\)
Lời giải chi tiết:
Thử từng đáp án ta có:
Đáp án A: \(y\left( 0 \right)=\tan 0-2=-2\ne 0\Rightarrow A\) sai.
Đáp án B: \(y\left( \frac{\pi }{4} \right)=\tan \frac{\pi }{4}-2=1-2=-1\Rightarrow B\) đúng.
Thử tương tự như trên ta thấy đáp án C và D đều sai.
Chọn B.
Câu hỏi 28 :
Cho các hàm số \(y=\cos x,\,\,y=\sin \,x,\,y=\tan \,x,\,y=\cot \,x\). Trong các hàm số trên, có bao nhiêu hàm số chẵn?
- A 2
- B 1
- C 3
- D 4
Đáp án: B
Phương pháp giải:
Hàm số \(y=f(x)\) với tập xác định D gọi là hàm số chẵn nếu : \(\forall x\in D\)thì \(-x\in D\)và \(f(-x)=f(x)\)
Hàm số \(y=f(x)\) với tập xác định D gọi là hàm số lẻ nếu : \(\forall x\in D\)thì \(-x\in D\)và \(f(-x)=-f(x)\)
Lời giải chi tiết:
Trong các hàm số \(y=\cos x,\,\,y=\sin \,x,\,y=\tan \,x,\,y=\cot \,x\), chỉ có duy nhất hàm số \(y=\cos x\) là hàm số chẵn.
Chọn B.
Câu hỏi 29 :
Xét sự biến thiên của hàm số \(y = 1 - \sin x\) trên một chu kì tuần hoàn của nó. Trong các kết luận sau, kết luận nào sai?
- A Hàm số đã cho nghịch biến trên khoảng \(\left( { - \dfrac{\pi }{2};0} \right)\).
- B Hàm số đã cho nghịch biến trên khoảng \(\left( {0;\dfrac{\pi }{2}} \right)\).
- C Hàm số đã cho đồng biến trên khoảng \(\left( {\dfrac{\pi }{2};\pi } \right)\).
- D Hàm số đã cho nghịch biến trên khoảng \(\left( {\dfrac{\pi }{2};\dfrac{{3\pi }}{2}} \right)\).
Đáp án: D
Phương pháp giải:
Hàm số
\(y = \sin x\) đồng biến trên các khoảng \(\left( { - \dfrac{\pi }{2} + k2\pi ;\,\,\dfrac{\pi }{2} + k2\pi } \right)\), nghịch biến trên các khoảng \(\left( {\dfrac{\pi }{2} + k2\pi ;\,\,\dfrac{{3\pi }}{2} + k2\pi } \right)\).
Lời giải chi tiết:
Hàm số đã cho tuần hoàn với chu kì \(2\pi \) và kết hợp với các đáp án ta xét sự biến thiên của hàm số trên đoạn \(\left[ { - \dfrac{\pi }{2};\dfrac{{3\pi }}{2}} \right]\).
- Hàm số \(y = \sin x\) đồng biến trên \(\left( { - \dfrac{\pi }{2};\dfrac{\pi }{2}} \right)\) nên hàm số \(y = 1 - \sin x\) nghịch biến trên \(\left( { - \dfrac{\pi }{2};\dfrac{\pi }{2}} \right)\).
- Hàm số \(y = \sin x\) nghịch biến trên \(\left( {\dfrac{\pi }{2};\dfrac{{3\pi }}{2}} \right)\) nên hàm số \(y = 1 - \sin x\) đồng biến trên \(\left( {\dfrac{\pi }{2};\dfrac{{3\pi }}{2}} \right)\).
Do đó chỉ có đáp án D là sai.
Chọn D.
Câu hỏi 30 :
Hình nào dưới đây biểu diễn đồ thị hàm số \(y = f\left( x \right) = 2\sin 2x\).
- A
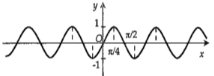
- B
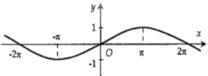
- C
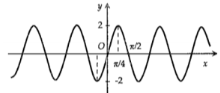
- D
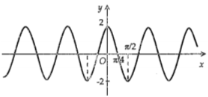
Đáp án: C
Phương pháp giải:
- Dựa vào tập giá trị của hàm sin.
- Dựa vào điểm đi qua của đồ thị hàm số.
Lời giải chi tiết:
Ta có: \( - 2 \le \sin 2x \le 2\) nên loại đáp án A và B.
Cho \(x = 0 \Rightarrow y = 2\sin 0 = 0\), do đó đồ thị hàm số \(y = f\left( x \right) = 2\sin 2x\) đi qua điểm (0;0). Loại đáp án D.
Chọn C.
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
 |
 |
 |
 |
 |
 |
 |
 |









