25 bài tập tổng hợp Hai góc đối đỉnh
Làm đề thiCâu hỏi 1 :
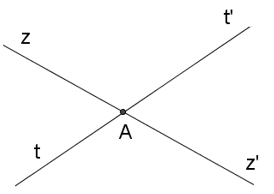
Hai đường thẳng zz’ và tt’ cắt nhau tại A. Góc đối đỉnh với \(\widehat{zAt}\) là:
- A \(\widehat{z'At'}\)
- B \(\widehat{z'At}\)
- C \(\widehat{zAt'}\)
- D \(\widehat{zAt}\)
Đáp án: A
Phương pháp giải:
Áp dụng định nghĩa hai góc đối đỉnh, xác định tia đối của tia Az và At, từ đó xác định góc đối đỉnh với \(\widehat{zAt}\)
Lời giải chi tiết:
Vì hai đường thẳng zz’ và tt’ cắt nhau tại A nên Az’ là tia đối của tia Az, At’ là tia đối của tia At.
Vậy góc đối đỉnh với \(\widehat{zAt}\) là \(\widehat{z'At'}\)
Chọn A.
Câu hỏi 2 :
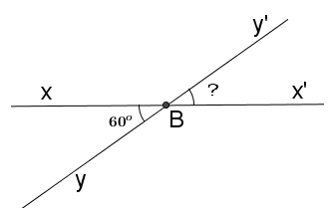
Vẽ góc xBy có số đo bằng 60o. Vẽ góc đối đỉnh với góc xBy. Tính số đo góc này.
- A 30o
- B 120o
- C 90o
- D
60o
Đáp án: D
Phương pháp giải:
Áp dụng tính chất: Hai góc đối đỉnh thì bằng nhau.
Lời giải chi tiết:
Vẽ \(\widehat{x'By'}\) là góc đối đỉnh với \(\widehat{xBy}\). Khi đó:
\(\widehat{x'By'}=\widehat{xBy}={{60}^{o}}\) (tính chất hai góc đối đỉnh)
Chọn D.
Câu hỏi 3 :
Hai đường thẳng zz’ và tt’ cắt nhau tại \(A\). Góc đối đỉnh với \(\widehat {zAt'}\) là:
- A \(\widehat {z'At'}\)
- B \(\widehat {z'At}\)
- C \(\widehat {zAt'}\)
- D \(\widehat {zAt}\)
Đáp án: B
Phương pháp giải:
Áp dụng định nghĩa hai góc đối đỉnh, xác định tia đối của tia Az và At, từ đó xác định góc đối đỉnh với \(\widehat {zAt}\).
Lời giải chi tiết:
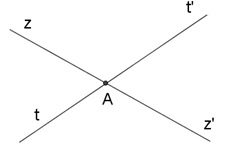
Vì hai đường thẳng \(zz'\) và \(tt'\) cắt nhau tại \(A\) nên \(Az'\) là tia đối của tia \(Az,At'\) là tia đối của tia \(At.\) Vậy góc đối đỉnh với \(\widehat {zAt'}\) là \(\widehat {z'At}\).
Chọn B.
Câu hỏi 4 :
Cho góc \(xOy\) đối đỉnh với góc \(x'Oy'\) và \(\widehat {xOy} = 60^\circ \) . Tính số đo góc
- A 30o
- B 120o
- C 90o
- D 60o
Đáp án: D
Phương pháp giải:
Áp dụng tính chất: Hai góc đối đỉnh thì bằng nhau.
Lời giải chi tiết:
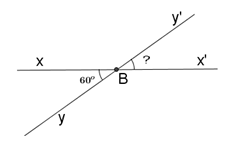
Vẽ \(\widehat {x'By'}\) là góc đối đỉnh với \(\widehat {xBy}\). Khi đó:
\(\widehat {x'By'} = \widehat {xBy} = {60^o}\) (tính chất hai góc đối đỉnh)
Chọn D.
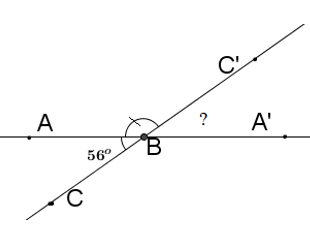
Câu hỏi 5 :
Vẽ \(\widehat{ABC}={{56}^{o}}\). Vẽ \(\widehat{ABC'}\) kề bù với \(\widehat{ABC}\). Sau đó vẽ tiếp \(\widehat{C'BA'}\) kề bù với \(\widehat{ABC'}\). Tính số đo \(\widehat{C'BA'}\).
- A 124o
- B 142o
- C
65o
- D
56o
Đáp án: D
Phương pháp giải:
Áp dụng tính chất hai góc kề bù, xác định các tia đối từ đó xác định góc đối đỉnh. Áp dụng tính chất hai góc đối đỉnh để tính góc C’BA’.
Lời giải chi tiết:
Vì góc ABC’ kề bù với góc ABC nên BC’ là tia đối của tia BC.
Vì góc C’BA’ kề bù với góc ABC’ nên BA’ là tia đối của tia BA
Do đó, góc C’BA’ và góc ABC đối đỉnh
\(\Rightarrow \widehat{C'BA'}=\widehat{ABC}={{56}^{o}}\)
Chọn D.
Câu hỏi 6 :
Cho hình vẽ sau. Biết góc xOy’ đối đỉnh với góc x’Oy, biết \(\widehat{xOy'}={{\widehat{O}}_{1}}={{165}^{o}}\) Tính các góc đỉnh O (khác góc bẹt).
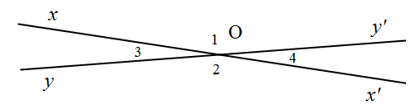
- A \({{\widehat{O}}_{2}}={{165}^{o}};\,{{\widehat{O}}_{3}}={{15}^{o}};\,\,{{\widehat{O}}_{4}}={{165}^{o}}\,\,\)
- B \({{\widehat{O}}_{2}}={{165}^{o}};\,{{\widehat{O}}_{3}}={{15}^{o}};\,\,{{\widehat{O}}_{4}}={{15}^{o}}\,\,\)
- C \({{\widehat{O}}_{2}}={{15}^{o}};\,{{\widehat{O}}_{3}}={{15}^{o}};\,\,{{\widehat{O}}_{4}}={{165}^{o}}\,\,\)
- D \({{\widehat{O}}_{2}}={{15}^{o}};\,{{\widehat{O}}_{3}}={{165}^{o}};\,\,{{\widehat{O}}_{4}}={{15}^{o}}\,\,\)
Đáp án: B
Phương pháp giải:
Áp dụng tính chất hai góc đối đỉnh, hai góc kề bù để tính các góc còn lại.
Lời giải chi tiết:
\({{\widehat{O}}_{2}}={{\widehat{O}}_{1}}={{165}^{o}}\) (tính chất hai góc đối đỉnh)
Góc O1 và góc O4 là hai góc kề bù
\(\begin{align} & \Rightarrow {{\widehat{O}}_{1}}+{{\widehat{O}}_{4}}={{180}^{o}} \\ & \Rightarrow {{\widehat{O}}_{4}}={{180}^{o}}-{{\widehat{O}}_{1}} \\ & \Rightarrow {{\widehat{O}}_{4}}={{180}^{o}}-{{165}^{o}}={{15}^{o}}. \\ \end{align}\)
\({{\widehat{O}}_{3}}={{\widehat{O}}_{4}}={{15}^{o}}\,\) (hai góc đối đỉnh)
Chọn B.
Câu hỏi 7 :
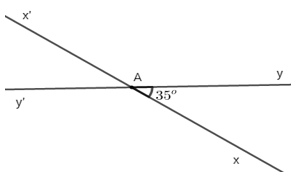
a) Vẽ góc xAy có số đo bằng 35o.
b) Vẽ góc x’Ay’ đối đỉnh với góc xAy.
c) Viết tên các góc có số đo bằng 35o.
d) Viết tên các góc có số đo bằng 145o.
Phương pháp giải:
Vẽ hình. Áp dụng tính chất hai góc đối đỉnh, tính chất hai góc kề bù để tính các góc còn lại.
Lời giải chi tiết:
c) Hai góc có số đo bằng 35o là : \(\widehat{xAy}\,\,;\,\,\widehat{x'Ay'}\)
d) Hai góc có số đo bằng 145o là : \(\widehat{xAy'}\,\,;\,\,\widehat{x'Ay}\)
Câu hỏi 8 :
Nếu góc xOy = 470 thì số đo của góc đối đỉnh với góc xOy bằng bao nhiêu?
- A 1330
- B 470
- C 430
- D 740
Đáp án: B
Phương pháp giải:
Vận dụng kiến thức về tính chất của 2 góc đối đỉnh.
Lời giải chi tiết:
2 góc đối đỉnh bằng nhau. Suy ra, góc đối đỉnh với góc xOy bằng số đo góc xOy và bằng 470.
Chọn B.
Câu hỏi 9 :
Đường thẳng \(xx'\) cắt đường thẳng \(yy'\) tại \(O,\) biết \(\widehat {xOy'} = 50^\circ ,\) số đo góc \(x'Oy\) bằng bao nhiêu ?
- A \(140^\circ .\)
- B \(130^\circ .\)
- C \(40^\circ .\)
- D \(50^\circ .\)
Đáp án: D
Phương pháp giải:
- Vẽ hình.
- Vận dụng định lý : Hai góc đối đỉnh thì bằng nhau.
Lời giải chi tiết:
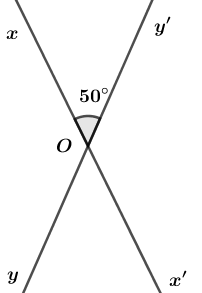
Ta có : \(Ox\) là tia đối của \(Ox'\); \(Oy\) là tia đối của \(Oy'\) (do cách vẽ)
Vậy \(\widehat {xOy'}\) và \(\widehat {x'Oy}\) là hai góc đối đỉnh
\( \Rightarrow \widehat {xOy'} = \widehat {x'Oy} = 50^\circ .\)
Chọn D.
Câu hỏi 10 :
Cho hai đường thẳng \(xx'\) và \(yy'\) giao nhau tại \(O\) sao cho \(\widehat {xOy} = 45^\circ \) . Chọn câu sai.
- A \(\widehat {x'Oy} = 135^\circ \)
- B \(\widehat {x'Oy'} = 45^\circ \)
- C \(\widehat {xOy'} = 135^\circ \)
- D \(\widehat {x'Oy'} = 135^\circ \)
Đáp án: D
Phương pháp giải:
+ Sử dụng tính chất: Hai góc đối đỉnh thì bằng nhau
+ Sử dụng: Tổng hai góc kề bù bằng \(180^\circ .\)
Lời giải chi tiết:
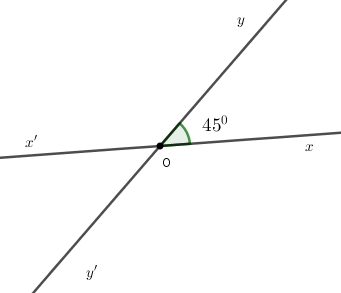
Vì hai đường thẳng \(xx'\) và \(yy'\) cắt nhau tại \(O\) nên \(Ox'\) là tia đối của tia \(Ox;Oy'\) là tia đối của tia \(Oy.\)
Suy ra \(\widehat {xOy}\) và \(\widehat {x'Oy'}\) ; \(\widehat {x'Oy}\) và \(\widehat {xOy'}\) là hai cặp góc đối đỉnh.
Do đó \(\widehat {x'Oy'} = \widehat {xOy} = 45^\circ \) và \(\widehat {x'Oy} = \widehat {xOy'}\)
Lại có \(\widehat {xOy}\) và \(\widehat {x'Oy}\) là hai góc ở vị trí kề bù nên \(\widehat {xOy} + \widehat {x'Oy} = 180^\circ \) \( \Rightarrow 45^\circ + \widehat {x'Oy} = 180^\circ \Rightarrow \widehat {x'Oy} = 180^\circ - 45^\circ \)
\( \Rightarrow \widehat {x'Oy} = 135^\circ \)
Vậy \(\widehat {x'Oy'} = \widehat {xOy} = 45^\circ \) và \(\widehat {x'Oy} = \widehat {xOy'} = 135^\circ .\)
Suy ra A, B, C đúng, D sai.
Chọn D.
Câu hỏi 11 :
Cho cặp góc đối đỉnh \(\widehat {tOz}\) và \(\widehat {t'Oz'}\) (\(Oz\) và \(Oz'\) là hai tia đối nhau). Biết \(\widehat {tOz'} = 4.\widehat {tOz}\). Tính các góc \(\widehat {tOz}\) và \(\widehat {t'Oz'}.\)
- A \(\widehat {zOt} = \widehat {z'Ot'} = 72^\circ \)
- B \(\widehat {zOt} = \widehat {z'Ot'} = 30^\circ \)
- C \(\widehat {zOt} = \widehat {z'Ot'} = 36^\circ \)
- D \(\widehat {zOt} = 72^\circ ;\,\widehat {z'Ot'} = 36^\circ \)
Đáp án: C
Phương pháp giải:
+ Sử dụng: Tổng hai góc kề bù bằng \(180^\circ .\)
+ Sử dụng tính chất: Hai góc đối đỉnh thì bằng nhau
Lời giải chi tiết:
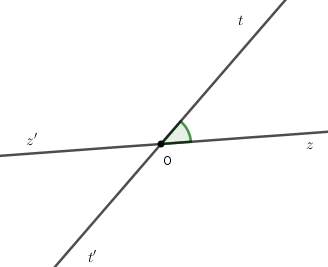
Ta có \(\widehat {zOt} + \widehat {tOz'} = 180^\circ \) (hai góc kề bù) \( \Rightarrow \widehat {zOt} + 4.\widehat {zOt} = 180^\circ \) \( \Rightarrow 5.\widehat {zOt} = 180^\circ \Rightarrow \widehat {zOt} = 36^\circ \)
Vì \(\widehat {tOz}\) và \(\widehat {t'Oz'}\) là hai góc đối đỉnh nên \(\widehat {zOt} = \widehat {z'Ot'} = 36^\circ .\)
Chọn C.
Câu hỏi 12 :
Vẽ \(\widehat {ABC} = {56^o}\). Vẽ \(\widehat {ABC'}\) kề bù với \(\widehat {ABC}\). Sau đó vẽ tiếp \(\widehat {C'BA'}\) kề bù với \(\widehat {ABC'}\). Tính số đo \(\widehat {C'BA'}\).
- A \({124^0}\)
- B \({142^0}\)
- C \({65^0}\)
- D \({56^0}\)
Đáp án: D
Phương pháp giải:
Áp dụng tính chất hai góc kề bù, xác định các tia đối từ đó xác định góc đối đỉnh. Áp dụng tính chất hai góc đối đỉnh để tính góc \(C'BA'.\)
Lời giải chi tiết:
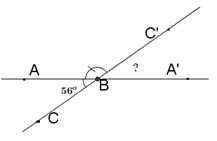
Vì góc \(ABC'\) kề bù với góc \(ABC\) nên \(BC'\) là tia đối của tia \(BC.\)
Vì góc \(C'BA'\) kề bù với góc \(ABC'\) nên \(BA'\) là tia đối của tia \(BA.\)
Do đó, góc \(C'BA'\) và góc \(ABC\) đối đỉnh.
\( \Rightarrow \widehat {C'BA'} = \widehat {ABC} = {56^o}\)
Chọn D.
Câu hỏi 13 :
Cho hình vẽ sau. Biết góc \(xOy'\) đối đỉnh với góc \(x'Oy,\) biết \(\widehat {xOy'} = {\widehat O_1} = {165^o}\). Tính các góc đỉnh O (khác góc bẹt).

- A \({\widehat O_2} = {165^o};\,{\widehat O_3} = {15^o};\,\,{\widehat O_4} = {165^o}\,\,\)
- B \({\widehat O_2} = {165^o};\,{\widehat O_3} = {15^o};\,\,{\widehat O_4} = {15^o}\,\,\)
- C \({\widehat O_2} = {15^o};\,{\widehat O_3} = {15^o};\,\,{\widehat O_4} = {165^o}\,\,\)
- D \({\widehat O_2} = {15^o};\,{\widehat O_3} = {165^o};\,\,{\widehat O_4} = {15^o}\,\,\)
Đáp án: B
Phương pháp giải:
Áp dụng tính chất hai góc đối đỉnh, hai góc kề bù để tính các góc còn lại.
Lời giải chi tiết:
\({\widehat O_2} = {\widehat O_1} = {165^o}\) (tính chất hai góc đối đỉnh)
Góc \({O_1}\) và góc \({O_4}\) là hai góc kề bù
\( \Rightarrow {\widehat O_1} + {\widehat O_4} = {180^o}\)
\( \Rightarrow {\widehat O_4} = {180^o} - {\widehat O_1}\)
\( \Rightarrow {\widehat O_4} = {180^o} - {165^o} = {15^o}\)
\({\widehat O_3} = {\widehat O_4} = {15^o}\,\) (hai góc đối đỉnh)
Chọn B.
Câu hỏi 14 :
Vẽ góc \(xOy\) có số đo bằng \({35^0}\). Vẽ góc \(x'Oy'\) đối đỉnh với góc \(xOy.\) Viết tên các góc có số đo bằng \({145^0}.\)
- A \(\widehat {xOy'}\,\,;\,\,\widehat {x'Oy'}\)
- B \(\widehat {xOy}\,\,;\,\,\widehat {x'Oy'}\)
- C \(\widehat {xOy'}\,\,;\,\,\widehat {x'Oy}\)
- D \(\widehat {xOy'}\,\,;\,\,\widehat {xOy}\)
Đáp án: C
Phương pháp giải:
Áp dụng tính chất hai góc đối đỉnh, tính chất hai góc kề bù để tính các góc còn lại.
Lời giải chi tiết:
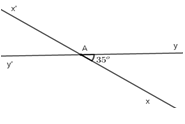
Vì hai đường thẳng \(xx'\) và \(yy'\) cắt nhau tại \(O\) nên \(Ox'\) là tia đối của tia \(Ox;Oy'\) là tia đối của tia \(Oy.\)
Suy ra \(\widehat {xOy}\) và \(\widehat {x'Oy'}\) ; \(\widehat {x'Oy}\) và \(\widehat {xOy'}\) là hai cặp góc đối đỉnh.
Do đó \(\widehat {x'Oy'} = \widehat {xOy} = 35^\circ \) và \(\widehat {x'Oy} = \widehat {xOy'}\)
Lại có \(\widehat {xOy}\) và \(\widehat {x'Oy}\) là hai góc ở vị trí kề bù nên \(\widehat {xOy} + \widehat {x'Oy} = 180^\circ \) \( \Rightarrow 35^\circ + \widehat {x'Oy} = 180^\circ \Rightarrow \widehat {x'Oy} = 180^\circ - 35^\circ \)
\( \Rightarrow \widehat {x'Oy} = 145^\circ \)
Vậy \(\widehat {x'Oy'} = \widehat {xOy} = 45^\circ \) và \(\widehat {x'Oy} = \widehat {xOy'} = 145^\circ .\)
Hai góc có số đo bằng \({145^o}\) là : \(\widehat {xOy'}\,\,;\,\,\widehat {x'Oy}\)
Chọn C.
Câu hỏi 15 :
Hai đường thẳng xy và x’y’ cắt nhau tại O. Biết \(\widehat{xOx'}={{70}^{o}}\). Ot là tia phân giác của góc xOx’. Ot’ là tia đối của tia Ot. Tính số đo góc yOt’.
- A \(\widehat{yOt'}={{35}^{o}}\)
- B \(\widehat{yOt'}={{70}^{o}}\)
- C \(\widehat{yOt'}={{145}^{o}}\)
- D \(\widehat{yOt'}={{110}^{o}}\)
Đáp án: A
Phương pháp giải:
Sử dụng tính chất tia phân giác của một góc. Áp dụng tính chất hai góc đối đỉnh để tính số đo góc yOt’.
Lời giải chi tiết:
Vì Ot là tia phân giác của góc xOx’nên
\(\widehat{xOt}=\widehat{tOx'}=\frac{1}{2}\widehat{xOx'}=\frac{1}{2}{{.70}^{o}}={{35}^{o}}\)
Vì Oy là tia đối của Ox, Ot’ là tia đối của Ot
\(\Rightarrow \widehat{yOt'}=\widehat{xOt}={{35}^{o}}\) (tính chất hai góc đối đỉnh).
Chọn A.
Câu hỏi 16 :
Hai đường thẳng MN và PQ cắt nhau tại A. Biết \(\widehat{MAQ}+\widehat{NAP}={{250}^{o}}\). Tính số đo góc NAP.
- A \(\widehat{NAP}={{250}^{o}}\)
- B \(\widehat{NAP}={{55}^{o}}\)
- C \(\widehat{NAP}={{125}^{o}}\)
- D \(\widehat{NAP}={{110}^{o}}\)
Đáp án: C
Phương pháp giải:
Áp dụng tính chất hai góc đối đỉnh. Thay vào biểu thức đã cho, tính góc NAP.
Lời giải chi tiết:
Vì AM là tia đối của AN, AQ là tia đối của AP
\(\Rightarrow \widehat{MAQ}=\widehat{NAP}\) (tính chất hai góc đối đỉnh)
Ta có :
\(\begin{align} & \,\,\,\,\,\,\widehat{MAQ}+\widehat{NAP}={{250}^{o}} \\ & \Rightarrow \widehat{NAP}+\widehat{NAP}={{250}^{o}} \\ & \Leftrightarrow 2\widehat{NAP}={{250}^{o}} \\ & \Leftrightarrow \widehat{NAP}={{125}^{o}} \\ \end{align}\)
Chọn C.
Câu hỏi 17 :
Hai đường thẳng MN và PQ cắt nhau tại O, tạo thành góc MOP có số đo bằng 80o.
a) Tính số đo của các góc còn lại.
b) Vẽ tia Ot là tia phân giác của góc MOP, Ot’ là tia đối của tia Ot. Chứng minh Ot’ là tia phân giác của góc NOQ.
c) Kể tên các cặp góc đối đỉnh là góc nhọn.
- A a) \(\widehat{NOQ}=\widehat{MOP}={{80}^{o}}\); \(\widehat{MOQ}=\widehat{PON}={{100}^{o}}\)
c) \(\widehat{MOP} \) và\( \widehat{NOQ}\) ,\( \widehat{ MOt}\) và \(\widehat{NOt’}\), \(\widehat{POt}\) và \(\widehat{ t’OQ.}\)
- B a) \(\widehat{NOQ}=\widehat{MOP}={{100}^{o}}\); \(\widehat{MOQ}=\widehat{PON}={{80}^{o}}\)
c) \(\widehat{MOP} \) và\( \widehat{NOQ}\) ,\( \widehat{ MOt}\) và \(\widehat{NOt’}\), \(\widehat{POt}\) và \(\widehat{ t’OQ.}\)
- C a) \(\widehat{NOQ}=\widehat{PON}={{80}^{o}}\); \(\widehat{MOQ}=\widehat{MOP}={{100}^{o}}\)
c) \(\widehat{MOP} \) và\( \widehat{NOQ}\) ,\( \widehat{ MOt}\) và \(\widehat{NOt’}\), \(\widehat{POt}\) và \(\widehat{ t’OQ.}\)
- D a) \(\widehat{NOQ}=\widehat{MOP}={{80}^{o}}\); \(\widehat{MOQ}=\widehat{PON}={{100}^{o}}\)
c) \(\widehat{MOP} \) và\( \widehat{NOt'}\) ,\( \widehat{ MOt}\) và \(\widehat{NOt’}\), \(\widehat{POt}\) và \(\widehat{ MOP.}\)
Đáp án: A
Phương pháp giải:
a) Áp dụng tính chất 2 góc đối đỉnh, tính chất 2 góc kề bù. Tính các góc còn lại.
b) Áp dụng tính chất tia phân giác của một góc để tính 2 góc MOt, POt. Xác định tia đối, áp dụng tính chất hai góc đối đỉnh, tính 2 góc NOt’, QOt’. Từ đó chứng minh Ot’ là tia phân giác của góc NOQ.
c) Áp dụng định nghĩa hai góc đối đỉnh, kể tên các góc đối đỉnh.
Lời giải chi tiết:
a) \(\widehat{NOQ}=\widehat{MOP}={{80}^{o}}\) (tính chất hai góc đối đỉnh)
Vì góc MOP và PON là hai góc kề bù nên :
\(\begin{align} & \,\,\,\,\,\widehat{MOP}+\widehat{PON}={{180}^{o}} \\ & \Rightarrow {{80}^{o}}+\widehat{PON}={{180}^{o}} \\ & \Rightarrow \widehat{PON}={{180}^{o}}-{{80}^{o}}={{100}^{o}} \\ \end{align}\)
\(\widehat{MOQ}=\widehat{PON}={{100}^{o}}\) (tính chất hai góc đối đỉnh).
b) Vì Ot là tia phân giác của góc MOP nên \(\widehat{MOt}=\widehat{tOP}=\frac{1}{2}\widehat{MOP}=\frac{1}{2}{{.80}^{o}}={{40}^{o}}.\)
Vì Ot’ là tia đối của tia Ot, do đó :
\(\widehat{NOt'}=\widehat{MOt}={{40}^{o}}\,\,\,\) (hai góc đối đỉnh)
\(\widehat{t'OQ}=\widehat{tOP}={{40}^{o}}\,\,\,\,\) (hai góc đối đỉnh)
\(\Rightarrow \widehat{NOt'}=\widehat{t'OQ}\)
Mặt khác tia Ot’ nằm trong góc NOQ.
Vậy Ot’ là tia phân giác của góc NOQ.
c) Các cặp góc đối đỉnh mà mỗi góc đều là góc nhọn là :
Góc MOP và góc NOQ, góc MOt và góc NOt’, góc POt và góc t’OQ.
Chọn A
Câu hỏi 18 :
Cho đường thẳng AB và điểm O trên đường thẳng đó. Trên cùng một nửa mặt phẳng bờ AB vẽ hai tia OC và OD sao cho \(\widehat{AOC}=\widehat{BOD}={{50}^{o}}\)
a) Hai góc AOC và BOD có phải hai góc đối đỉnh không? Vì sao?
b) Trên nửa mặt phẳng bờ AB không chứa tia OD, vẽ tia OE sao cho tia OA là tia phân giác của góc COE. Hai góc BOD và AOE có phải là hai góc đối đỉnh không? Vì sao?
Phương pháp giải:
a) Xác định các tia đối, áp dụng định nghĩa hai góc đối đỉnh.
b) Áp dụng tính chất tia phân giác của một góc, tính góc AOE. Áp dụng tính chất tia phân giác của một góc, tính tổng hai góc, chứng minh góc kề bù, từ đó xác định tia đối, hai góc đối đỉnh.
Lời giải chi tiết:
a) Hai góc AOC và BOD có: OA và OB là hai tia đối nhau, OD và OC không phải là hai tia đối nhau.
Vậy hai góc đó không phải là hai góc đối đỉnh.
b) Vì BOD và DOA là hai góc kề bù nên:
\(\begin{align} & \,\,\,\,\,\widehat{BOD}+\widehat{DOA}={{180}^{O}} \\ & \Rightarrow {{50}^{O}}+\widehat{DOA}={{180}^{O}} \\ & \Rightarrow \widehat{DOA}={{180}^{O}}-{{50}^{O}}={{130}^{O}} \\ \end{align}\)
Tia OA là tia phân giác góc COE nên \(\widehat{AOE}=\widehat{AOC}={{50}^{O}}\).
Tia OD và tia OE thuộc hai nửa mặt phẳng đối nhau bờ chứa tia OA
nên tia OA nằm giữa hai tia OD và OE, ta có:
\(\widehat{DOA}+\widehat{AOE}={{130}^{0}}+{{50}^{0}}={{180}^{0}}\)
Suy ra OD và OE là hai tia đối nhau.
Hai góc BOD và AOE có hai cặp cạnh OB và OA, OD và OE là hai tia đối nhau nên là hai góc đối đỉnh.
Câu hỏi 19 :
Hai đường thẳng \(xy\) và \(x'y'\) cắt nhau tại \(O.\) Biết \(\widehat {xOx'} = {70^o}\). \(Ot\) là tia phân giác của góc xOx’. \(Ot'\) là tia đối của tia \(Ot.\) Tính số đo góc \(yOt'.\)
- A \(\widehat {yOt'} = {35^o}\)
- B \(\widehat {yOt'} = {70^o}\)
- C \(\widehat {yOt'} = {145^o}\)
- D \(\widehat {yOt'} = {110^o}\)
Đáp án: A
Phương pháp giải:
Sử dụng tính chất tia phân giác của một góC. Áp dụng tính chất hai góc đối đỉnh để tính số đo góc \(yOt'.\)
Lời giải chi tiết:
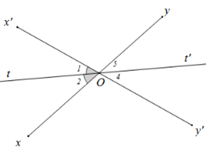
Vì \(Ot\) là tia phân giác của góc \(xOx'\) nên
\(\widehat {xOt} = \widehat {tOx'} = \frac{1}{2}\widehat {xOx'} = \frac{1}{2}{.70^o} = {35^o}\)
Vì \(Oy\) là tia đối của \(Ox,Ot'\) là tia đối của \(Ot\)
\( \Rightarrow \widehat {yOt'} = \widehat {xOt} = {35^o}\) (tính chất hai góc đối đỉnh).
Chọn A.
Câu hỏi 20 :
Hai đường thẳng \(MN\) và \(PQ\) cắt nhau tại \(O\), tạo thành góc \(MOP\) có số đo bằng \({80^o}.\)
Câu 1:
Chọn câu đúng.
- A \(\widehat {MOQ} = \widehat {PON} = {100^o}\)
- B \(\widehat {MOQ} = \widehat {PON} = {80^o}\)
- C \(\widehat {MOQ} + \widehat {PON} = {180^o}\)
- D \(\widehat {MOQ} = \widehat {PON} = {160^o}\)
Đáp án: A
Phương pháp giải:
Áp dụng tính chất \(2\) góc đối đỉnh, tính chất \(2\) góc kề bù. Tính các góc còn lại.
Lời giải chi tiết:
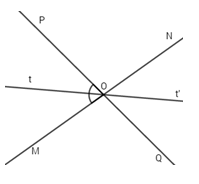
\(\widehat {NOQ} = \widehat {MOP} = {80^o}\) (tính chất hai góc đối đỉnh)
Vì góc \(MOP\) và \(PON\) là hai góc kề bù nên :
\(\,\widehat {MOP} + \widehat {PON} = {180^o} \Rightarrow {80^o} + \widehat {PON} = {180^o}\) \( \Rightarrow \widehat {PON} = {180^o} - {80^o} = {100^o}\)
Khi đó \(\widehat {MOQ} = \widehat {PON} = {100^o}\) (tính chất hai góc đối đỉnh).
Chọn A.
Câu 2:
Tia \(Ot\) là tia phân giác của góc \(MOP,\) \(Ot'\) là tia đối của tia \(Ot.\) Chọn câu đúng.
- A \(Ot'\) là tia phân giác của góc \(NOP.\)
- B \(Ot'\) là tia phân giác của góc \(NOQ.\)
- C \(ON\) là tia phân giác của góc \(t'OP.\)
- D Cả A, B, C đều sai.
Đáp án: B
Phương pháp giải:
Áp dụng tính chất tia phân giác của một góc để tính \(2\) góc \(MOt,POt.\) Xác định tia đối, áp dụng tính chất hai góc đối đỉnh, tính \(2\) góc \(NOt',QOt'.\) Từ đó chứng minh \(Ot'\) là tia phân giác của góc \(NOQ.\)
Lời giải chi tiết:
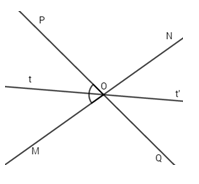
Vì \(Ot\) là tia phân giác của góc \(MOP\) nên \(\widehat {MOt} = \widehat {tOP} = \frac{1}{2}\widehat {MOP} = \frac{1}{2}{.80^o} = {40^o}.\)
Vì \(Ot'\) là tia đối của tia \(Ot,\) do đó :
\(\widehat {NOt'} = \widehat {MOt} = {40^o}\,\,\,\) (hai góc đối đỉnh)
\(\widehat {t'OQ} = \widehat {tOP} = {40^o}\,\,\,\,\) (hai góc đối đỉnh)
\( \Rightarrow \widehat {NOt'} = \widehat {t'OQ}\)
Mặt khác tia \(Ot'\) nằm trong góc \(NOQ.\) Vậy \(Ot'\) là tia phân giác của góc \(NOQ.\)
Chọn B.
Câu hỏi 21 :
Cho đường thẳng \(AB\) và điểm \(O\) trên đường thẳng đó. Trên cùng một nửa mặt phẳng bờ \(AB\) vẽ hai tia \(OC\) và \(OD\) sao cho \(\widehat {AOC} = \widehat {BOD} = {50^o}\). Trên nửa mặt phẳng bờ \(AB\) không chứa tia \(OD,\) vẽ tia \(OE\) sao cho tia \(OA\) là tia phân giác của góc \(COE.\) Chọn câu đúng?
- A \(\widehat {AOC};\widehat {BOD}\) là hai góc đối đỉnh.
- B \(OD\) và \(OE\) là hai tia đối nhau.
- C Hai góc \(BOD\) và \(AOE\) là hai góc đối đỉnh.
- D Cả B, C đều đúng.
Đáp án: D
Phương pháp giải:
+ Xác định các tia đối, áp dụng định nghĩa hai góc đối đỉnh.
+ Áp dụng tính chất tia phân giác của một góc, tính góc \(AOE.\) Áp dụng tính chất tia phân giác của một góc, tính tổng hai góc, chứng minh góc kề bù, từ đó xác định tia đối, hai góc đối đỉnh.
Lời giải chi tiết:
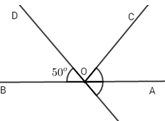
+ Hai góc \(AOC\) và \(BOD\) có: \(OA\) và \(OB\) là hai tia đối nhau, \(OD\) và \(OC\) không phải là hai tia đối nhau.
Vậy hai góc đó không phải là hai góc đối đỉnh.
+ Vì góc \(BOD\) và \(DOA\) là hai góc kề bù nên:
\(\begin{array}{l}\,\,\,\,\,\widehat {BOD} + \widehat {DOA} = {180^O}\\ \Rightarrow {50^O} + \widehat {DOA} = {180^O}\\ \Rightarrow \widehat {DOA} = {180^O} - {50^O} = {130^O}\end{array}\)
Tia \(OA\) là tia phân giác góc \(COE\) nên \(\widehat {AOE} = \widehat {AOC} = {50^O}\).
Tia \(OD\) và tia \(OE\) thuộc hai nửa mặt phẳng đối nhau bờ chứa tia \(OA\) nên tia \(OA\) nằm giữa hai tia \(OD\) và \(OE,\) ta có:
\(\widehat {DOA} + \widehat {AOE} = {130^0} + {50^0} = {180^0}\)
Suy ra \(OD\) và \(OE\) là hai tia đối nhau.
Hai góc \(BOD\) và \(AOE\) có hai cặp cạnh \(OB\) và \(OA,OD\) và \(OE\) là hai tia đối nhau nên là hai góc đối đỉnh.
Chọn D.
Câu hỏi 22 :
Cho \(\widehat {AOB} = 50^\circ \) , tia \(OC\) là tia phân giác của \(\widehat {AOB}\). Gọi \(OD\) là tia đối của tia \(OC\). Trên nửa mặt phẳng bờ \(CD\) chứa tia \(OA\), vẽ tia \(OE\) sao cho \(\widehat {DOE} = 25^\circ \). Góc nào dưới đây đối đỉnh với \(\widehat {DOE}\).
- A \(\widehat {DOA}\)
- B \(\widehat {COA}\)
- C \(\widehat {AOE}\)
- D \(\widehat {BOC}\)
Đáp án: D
Phương pháp giải:
+ Chứng minh \(OB\) và \(OE\) là hai tia đối nhau.
+ Từ đó suy ra cặp góc đối đỉnh theo định nghĩa.
Lời giải chi tiết:
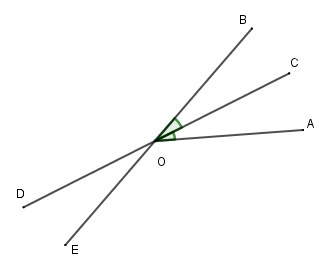
Vì \(OC\) và \(OD\) là hai tia đối nhau nên \(\widehat {COE}\) và \(\widehat {DOE}\) là hai góc kề bù. Khi đó \(\widehat {COE} + \widehat {DOE} = 180^\circ \) \( \Rightarrow \widehat {COE} = 180^\circ - 25^\circ = 155^\circ \)
Vì \(OC\) là tia phân giác của góc \(BOA\) nên \(\widehat {COB} = \frac{{\widehat {AOB}}}{2} = \frac{{50^\circ }}{2} = 25^\circ \)
Nhận thấy \(\widehat {BOC} + \widehat {COE} = 25^\circ + 155^\circ = 180^\circ \) nên \(OB\) và \(OE\) là hai tia đối nhau.
Suy ra \(\widehat {BOC}\) và \(\widehat {DOE}\) là hai góc đối đỉnh.
Chọn D.
Câu hỏi 23 :
Hai đường thẳng \(AB\) và \(CD\) cắt nhau tại \(O\) tạo thành \(\widehat {AOC} = 60^\circ \) . Gọi \(OM\) là phân giác \(\widehat {AOC}\) và \(ON\) là tia đối của tia \(OM\). Tính \(\widehat {BON}\) và \(\widehat {DON}.\)
- A \(\widehat {BON} = \widehat {DON} = 25^\circ \)
- B \(\widehat {BON} = \widehat {DON} = 30^\circ \)
- C \(\widehat {BON} = \widehat {DON} = 60^\circ \)
- D \(\widehat {BON} = \widehat {DON} = 45^\circ \)
Đáp án: B
Phương pháp giải:
+ Sủ dụng tính chất tia phân giác tính các góc \(\widehat {AOM};\widehat {COM}\)
+ Sử dụng tính chất hai góc đối đỉnh để suy ra hai góc \(\widehat {BON}\) và \(\widehat {DON}.\)
Lời giải chi tiết:

Vì \(AB\) và \(CD\) cắt nhau tại \(O\) nên \(OA\) và \(OB\) là hai tia đối nhau, \(OC\) và \(OD\) là hai tia đối nhau.
Vì \(OM\) là tia phân giác \(\widehat {COA}\) nên \(\widehat {AOM} = \widehat {COM} = \frac{{\widehat {COA}}}{2} = \frac{{60}}{2} = 30^\circ \)
Mà \(ON\) và \(OM\) là hai tia đối nhau nên \(\widehat {AOM}\) và \(\widehat {BON}\) là hai góc đối đỉnh; \(\widehat {COM}\) và \(\widehat {DON}\) là hai góc đối đỉnh
Suy ra \(\widehat {AOM} = \widehat {BON} = 30^\circ ;\widehat {COM} = \widehat {DON} = 30^\circ \) hay \(\widehat {BON} = \widehat {DON} = 30^\circ .\)
Chọn B.
Câu hỏi 24 :
Hai đường thẳng \(AB\) và \(CD\) cắt nhau tại \(O.\) Biết \(\widehat {AOC} - \widehat {AOD} = {50^0}.\) Chọn câu sai.
- A \(\widehat {AOC} = 110^\circ \)
- B \(\widehat {BOC} = 65^\circ \)
- C \(\widehat {BOD} = 120^\circ \)
- D \(\widehat {AOD} = 50^\circ \)
Đáp án: B
Phương pháp giải:
+ Sử dụng: Tổng hai góc kề bù bằng \(180^\circ .\)
+ Sử dụng tính chất: Hai góc đối đỉnh thì bằng nhau
Lời giải chi tiết:
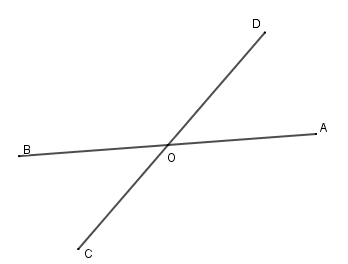
Vì \(\widehat {AOD}\) và \(\widehat {AOC}\) là hai góc kề bù nên \(\widehat {AOD} + \widehat {AOC} = 180^\circ \) mà \(\widehat {AOC} - \widehat {AOD} = 50^\circ \)
Nên \(\widehat {AOC} = \frac{{180^\circ + 50^\circ }}{2} = 115^\circ \) và \(\widehat {AOD} = 180^\circ - \widehat {AOC} = 65^\circ \)
Mà \(\widehat {AOD}\) và \(\widehat {BOC}\) là hai góc đối đỉnh nên \(\widehat {BOC} = \widehat {AOD} = 65^\circ .\)
Lại có \(\widehat {BOD}\) và \(\widehat {AOC}\) là hai góc đối đỉnh nên \(\widehat {BOD} = \widehat {AOC} = 115^\circ .\)
Vậy \(\widehat {BOD} = \widehat {AOC} = 115^\circ ;\,\widehat {BOC} = \widehat {AOD} = 65^\circ .\)
Chọn B.
Câu hỏi 25 :
Cho góc vuông AOB và tia OC nằm trong góc đó. Vẽ tia Ox sao cho OA là tia phân giác của góc xOC, vẽ tia Oy sao cho OB là tia phân giác của góc yOC, vẽ tia OD là tia đối của tia OC. Chứng minh góc xOD và góc COy là hai góc đối đỉnh.
Phương pháp giải:
Áp dụng tính chất tia phân giác của góc, cộng góc tính góc xOy để chứng minh Ox là tia đối cuả tia Oy. Từ đó chứng minh góc xOD đối đỉnh với góc COy.
Lời giải chi tiết:
Vì OA là tia phân giác của góc xOC nên \(\widehat{xOA}=\widehat{AOC}\)
Vì OB là tia phân giác của góc yOC nên \(\widehat{COB}=\widehat{BOy}\)
Vì OC nằm giữa tia OA và OB nên:
\(\begin{align} & \,\,\,\,\,\widehat{AOC}+\widehat{COB}={{90}^{0}} \\ & \Rightarrow \widehat{xOA}+\widehat{BOy}={{90}^{0}} \\ \end{align}\)
Ta có: \(\widehat{xOy}=\widehat{xOA}+\widehat{AOB}+\widehat{BOy}=\widehat{AOB}+\left( \widehat{xOA}+\widehat{BOy} \right)={{90}^{0}}+{{90}^{0}}={{180}^{0}}\)
Do đó, Ox là tia đối của tia Oy.
Mà OC là tia đối của tia OD.
Vậy góc xOD và góc COy là hai góc đối đỉnh.
>> Học trực tuyến lớp 7 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 7 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
 |
 |
 |
 |
 |
 |
Các bài khác cùng chuyên mục