25 bài tập tổng hợp Hai đường thẳng song song
Làm đề thiCâu hỏi 1 :
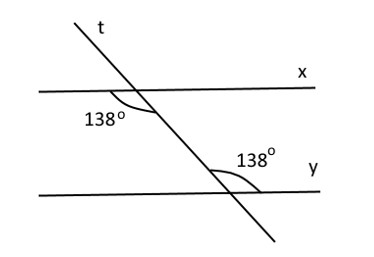
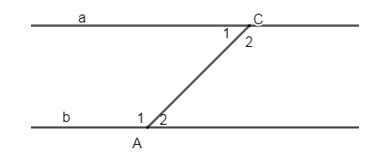
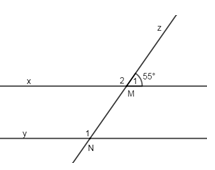
Cho hình vẽ sau:
Em hãy chọn kết luận đúng:
- A \(x//y\) vì có hai góc đồng vị bằng nhau.
- B \(x//y\) vì có hai góc so le trong bằng nhau.
- C \(x//t\) vì có hai góc so le trong bằng nhau.
- D \(t//y\) vì có hai góc so le trong bằng nhau.
Đáp án: B
Phương pháp giải:
Áp dụng dấu hiệu nhận biết hai đường thẳng song song: Nếu đường thẳng c cắt hai đường thẳng a và b, trong các góc tạo thành có 1 cặp góc so le trong bằng nhau thì \(a//b\).
Lời giải chi tiết:
Từ hình vẽ ta có đường thẳng t cắt hai đường thẳng x và y, tạo thành 1 cặp góc so le trong bằng nhau (cùng bằng \({{138}^{0}}\)) nên suy ra \(x//y\).
Chọn B.
Câu hỏi 2 :
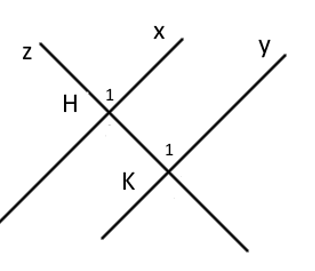
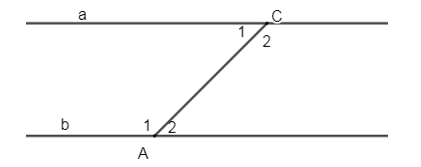
Cho đường thẳng z cắt hai đường thẳng x và y. Nhận định nào sau đây có thể chỉ ra hai đường thẳng x và y song song ?
- A \(\widehat{{{H}_{1}}}=\widehat{{{K}_{1}}}\) (hai góc đồng vị)
- B \(\widehat{{{H}_{1}}}=\widehat{{{K}_{1}}}\) (hai góc so le trong)
- C \(\widehat{{{H}_{1}}}=\widehat{{{K}_{1}}}\) (hai góc đối đỉnh)
- D \(\widehat{{{H}_{1}}}=\widehat{{{K}_{1}}}\) (hai góc trong cùng phía)
Đáp án: A
Phương pháp giải:
Áp dụng dấu hiệu nhận biết hai đường thẳng song song: Nếu đường thẳng c cắt hai đường thẳng a và b, trong các góc tạo thành có 1 cặp góc đồng vị bằng nhau thì \(a//b\).
Lời giải chi tiết:
Vì \(\widehat{{{H}_{1}}}\) và \(\widehat{{{K}_{1}}}\) là hai góc đồng vị nên để \(x//y\Leftrightarrow \widehat{{{H}_{1}}}=\widehat{{{K}_{1}}}\).
Chọn A.
Câu hỏi 3 :
Cho đường thẳng \(c\) cắt hai đường thẳng \(a\) và \(b\) và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì:
- A \(a//b\)
- B \(a\) cắt \(b\)
- C \(a \bot b\)
- D \(a\) trùng với \(b\)
Đáp án: A
Phương pháp giải:
Sử dụng dấu hiệu nhận biết hai đường thẳng song song.
Lời giải chi tiết:
Nếu đường thẳng \(c\)cắt hai đường thẳng \(a\) và \(b\) và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì \(a//b\).
Chọn A.
Câu hỏi 4 :
Chọn câu trả lời đúng trong các câu sau:
- A Hai đường thẳng không có điểm chung thì song song với nhau.
- B Hai đoạn thẳng không có điểm chung thì song song với nhau.
- C Hai đường thẳng phân biệt không cắt nhau thì song song với nhau.
- D Hai đường thẳng song song là hai đường thẳng không trùng nhau.
Đáp án: A
Phương pháp giải:
Sử dụng định nghĩa hai đường thẳng song song
Lời giải chi tiết:
Hai đường thẳng song song (trong mặt phẳng) là hai đường thẳng không có điểm chung.
Chọn A.
Câu hỏi 5 :
Chọn câu sai.
- A Nếu hai đường thẳng \(a,b\) cắt đường thẳng c tạo thành một cặp góc so le trong bằng nhau thì \(a//b.\)
- B Nếu hai đường thẳng \(a,b\) cắt đường thẳng c tạo thành một cặp góc đồng vị bằng nhau thì \(a//b.\)
- C Hai đường thẳng a, b cắt đường thẳng c và trong các góc tạo thành có một cặp góc so le ngoài bằng nhau thì \(a//b.\)
- D Cả A, B, C đều đúng.
Đáp án: D
Phương pháp giải:
Sử dụng dấu hiệu nhận biết hai đường thẳng song song
Lời giải chi tiết:
+ Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành một cặp góc so le trong bằng nhau thì hai đường thẳng song song.
+ Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành một cặp góc đồng vị bằng nhau thì hai đường thẳng song song.
+ Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành một cặp góc so le ngoài bằng nhau thì hai đường thẳng song song.
nên cả A, B, C đều đúng.
Chọn D.
Câu hỏi 6 :
Điền vào chỗ trống:
“Nếu hai đường thẳng \(d,d'\) cắt đường thẳng \(xy\) tạo thành một cặp góc trong cùng phía … thì \(d//d'\)”
- A bù nhau
- B bằng nhau
- C phụ nhau
- D kề nhau
Đáp án: A
Phương pháp giải:
Sử dụng dấu hiệu nhận biết hai đường thẳng song song
Lời giải chi tiết:
Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành một cặp góc trong cùng phía bù nhau thì hai đường thẳng song song.
Chọn A.
Câu hỏi 7 :
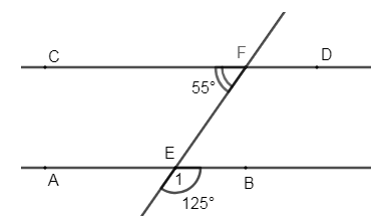
Cho hình vẽ:

Biết \(\widehat{CF\text{E}}={{55}^{0}},\,\widehat{{{E}_{1}}}={{125}^{0}}\) . Chứng minh \(AB//C\text{D}\).
Phương pháp giải:
Áp dụng dấu hiệu nhận biết hai đường thẳng song song: Nếu đường thẳng c cắt hai đường thẳng a và b, trong các góc tạo thành có 1 cặp góc so le trong bằng nhau thì \(a//b\).
Lời giải chi tiết:
Vì \(\widehat{{{E}_{1}}}\) và \(\widehat{BEF}\) là hai góc kề bù (gt)
\(\Rightarrow \widehat{{{E}_{1}}}+\widehat{BEF}={{180}^{0}}\Rightarrow \widehat{BEF}={{180}^{0}}-\widehat{{{E}_{1}}}={{180}^{0}}-{{125}^{0}}={{55}^{0}}\Rightarrow \widehat{BEF}=\widehat{CFE}={{55}^{0}}\)
Mà \(\widehat{BEF}\) và \(\widehat{CFE}\) là hai góc so le trong nên suy ra \(AB//C\text{D}\) (dấu hiệu nhận biết hai đường thẳng song song)
Câu hỏi 8 :
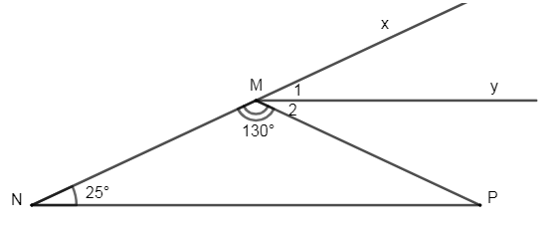
Cho \(\Delta MNP\) có \(\widehat{M}={{130}^{0}},\,\widehat{N}={{25}^{0}}\). Vẽ Mx là tia đối của tia MN, My là tia phân giác của \(\widehat{PM\text{x}}\) . Hỏi My có song song với NP không? Vì sao?
Phương pháp giải:
Áp dụng dấu hiệu nhận biết hai đường thẳng song song: Nếu đường thẳng c cắt hai đường thẳng a và b, trong các góc tạo thành có 1 cặp góc so le trong bằng nhau thì \(a//b\).
Lời giải chi tiết:
Xét \(\Delta MNP\) có:
\(\widehat{N}+\widehat{NMP}+\widehat{P}={{180}^{0}}\) (định lí tổng 3 góc trong tam giác)
\(\Rightarrow \widehat{P}={{180}^{0}}-\widehat{N}-\widehat{NMP}={{180}^{0}}-{{25}^{0}}-{{130}^{0}}={{25}^{0}}\) (1)
Ta có: \(\widehat{xMP}+\widehat{NMP}={{180}^{0}}\) (kề bù)
\(\Rightarrow \widehat{xMP}={{180}^{0}}-\widehat{NMP}={{180}^{0}}-{{130}^{0}}={{50}^{0}}\)
Mà My là tia phân giác của \(\widehat{xMP}\left( gt \right)\Rightarrow \widehat{{{M}_{1}}}=\widehat{{{M}_{2}}}=\frac{\widehat{xMP}}{2}={{50}^{0}}:2={{25}^{0}}\) (2)
Từ (1) và (2) \(\Rightarrow \widehat{P}=\widehat{{{M}_{2}}}\), mà hai góc này ở vị trí so le trong nên \(\Rightarrow My//\,NP\) (dấu hiệu nhận biết hai đường thẳng song song)
Câu hỏi 9 :
Cho ba đường thẳng \(a,\,\,b,\,\,c\) phân biệt. Biết \(a \bot c\) và \(b \bot c\) suy ra:
- A \(a\) trùng \(b\)
- B \(a\) // \(b\)
- C \(a\) và \(b\) cắt nhau
- D \(a \bot b\)
Đáp án: B
Phương pháp giải:
Áp dụng tính chất: Hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì chúng song song với nhau.
Lời giải chi tiết:
Ta có \(a \bot c\) và \(b \bot c\) suy ra \(a\)// \(b\) (theo quan hệ giữa tính vuông góc và tính song song).
Chọn B.
Câu hỏi 10 :
Hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng sẽ
- A song song với nhau
- B vuông góc với nhau
- C trùng nhau
- D cắt nhau
Đáp án: A
Phương pháp giải:
Áp dụng quan hệ giữa tính vuông góc và tính song song của ba đường thẳng.
Lời giải chi tiết:
Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau.
Chọn A.
Câu hỏi 11 :
Cho hình vẽ dưới đây:
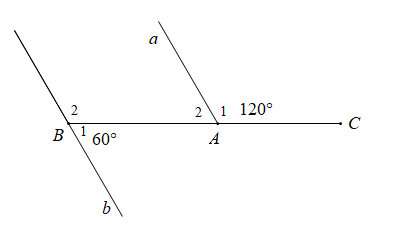
Chọn câu sai.
- A \(a \bot b\)
- B \(\widehat {{A_2}} = 60^\circ \)
- C \(\widehat {{B_2}} = 120^\circ \)
- D \(a//b\)
Đáp án: A
Phương pháp giải:
+ Áp dụng tính chất hai góc kề bù để tính \(\widehat {{A_2}};\,\widehat {{B_2}}.\)
+ Sử dụng dấu hiệu nhận biết để suy ra hai đường thẳng song song
Lời giải chi tiết:
Vì \(\widehat {{A_1}};\widehat {{A_2}}\) là hai góc kề bù nên \(\widehat {{A_1}} + \widehat {{A_2}} = 180^\circ \) \( \Rightarrow 120^\circ + \widehat {{A_2}} = 180^\circ \Rightarrow \widehat {{A_2}} = 60^\circ \)
Tương tự vì \(\widehat {{B_1}};\widehat {{B_2}}\) là hai góc kề bù nên \(\widehat {{B_1}} + \widehat {{B_2}} = 180^\circ \) \( \Rightarrow 60^\circ + \widehat {{B_2}} = 180^\circ \Rightarrow \widehat {{B_2}} = 120^\circ \)
Nhận thấy \(\widehat {{A_2}} = \widehat {{B_2}} = 120^\circ \) mà hai góc ở vị trí đồng vị nên \(a//b.\)
Vậy A sai.
Chọn A.
Câu hỏi 12 :
Cho hình vẽ dưới đây, biết \(a//b\). Tính \(x;y.\)
- A \(x = 80^\circ ;y = 80^\circ .\)
- B \(x = 60^\circ ;y = 80^\circ .\)
- C \(x = 80^\circ ;y = 60^\circ .\)
- D \(x = 60^\circ ;y = 60^\circ .\)
Đáp án: C
Phương pháp giải:
Áp dụng tính chất hai đường thẳng song song để tính \(x.\) Áp dụng tính chất hai góc đối đỉnh để tính \(y.\)
Lời giải chi tiết:
Vì \(a//b\) nên \(\widehat {BAC} + \widehat {ACD} = 180^\circ \) (hai góc trong cùng phía bù nhau)
Suy ra \(100^\circ + x = 180^\circ \Rightarrow x = 80^\circ \)
Tương tự ta có \(\widehat {ABD} + \widehat {CDB} = 180^\circ \Rightarrow \widehat {CDB} = 60^\circ \)
Suy ra \(y = \widehat {CDB} = 60^\circ \) (hai góc đổi đỉnh)
Vậy \(x = 80^\circ ;y = 60^\circ .\)
Chọn C.
Câu hỏi 13 :
Cho hình vẽ:
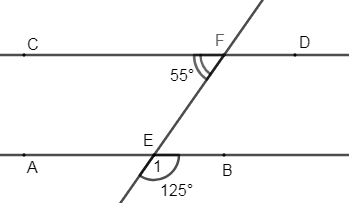
Biết \(\widehat {CF{\rm{E}}} = {55^0},\,\widehat {{E_1}} = {125^0}\) . Khi đó:
- A \(\widehat {AEF} = 125^\circ \)
- B
\(AB//C{\rm{D}}\)
- C Cả A, B đều đúng
- D Cả A, B đều sai
Đáp án: B
Phương pháp giải:
Áp dụng dấu hiệu nhận biết hai đường thẳng song song: Nếu đường thẳng \(c\) cắt hai đường thẳng \(a\) và \(b,\) trong các góc tạo thành có \(1\) cặp góc so le trong bằng nhau thì \(a//b\).
Lời giải chi tiết:
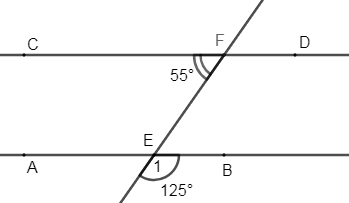
Vì \(\widehat {{E_1}}\) và \(\widehat {BEF}\) là hai góc kề bù (gt)
\( \Rightarrow \widehat {{E_1}} + \widehat {BEF} = {180^0} \Rightarrow \widehat {BEF} = {180^0} - \widehat {{E_1}} = {180^0} - {125^0} = {55^0} \Rightarrow \widehat {BEF} = \widehat {CFE} = {55^0}\)
Mà \(\widehat {BEF}\)và \(\widehat {CFE}\) là hai góc so le trong nên suy ra \(AB//C{\rm{D}}\) (dấu hiệu nhận biết hai đường thẳng song song)
Chọn B.
Câu hỏi 14 :
Cho hình vẽ sau, biết \(x//y\) và \(\widehat {{M_1}} = {55^0}\). Tính \(\widehat {{N_1}}\).
- A \({55^0}\)
- B \({35^0}\)
- C \({60^0}\)
- D \({125^0}\)
Đáp án: D
Phương pháp giải:
Áp dụng tính chất hai đường thẳng song song.
Lời giải chi tiết:
Ta có: \(\widehat {{M_1}} + \widehat {{M_2}} = {180^0} \Rightarrow \widehat {{M_2}} = {180^0} - {55^0} = {125^0}\) (kề bù)
Vì \(x//y\left( {gt} \right) \Rightarrow \widehat {{M_2}} = \widehat {{N_1}} = {125^0}\) (2 góc đồng vị)
Chọn D.
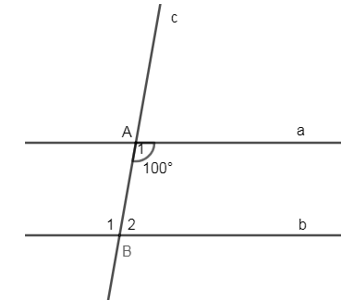
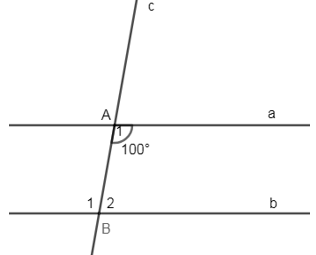
Câu hỏi 15 :
Cho hình vẽ sau, biết \(a//b\) và \(\widehat{{{A}_{1}}}={{100}^{0}}\). Tính \(\widehat{{{B}_{1}}},\widehat{{{B}_{2}}}\).
- A \(\widehat{{{B}_{1}}}=\widehat{{{B}_{2}}}={{100}^{0}}\)
- B \(\widehat{{{B}_{1}}}={{100}^{0}},\,\,\widehat{{{B}_{2}}}={{80}^{0}}\)
- C \(\widehat{{{B}_{1}}}={{80}^{0}},\,\,\widehat{{{B}_{2}}}={{100}^{0}}\)
- D \(\widehat{{{B}_{1}}}={{100}^{0}},\,\,\widehat{{{B}_{2}}}={{90}^{0}}\)
Đáp án: B
Phương pháp giải:
Áp dụng tính chất của hai đường thẳng song song.
Lời giải chi tiết:
Vì \(a//b\left( gt \right)\Rightarrow \widehat{{{A}_{1}}}=\widehat{{{B}_{1}}}\,={{100}^{0}}\) (hai góc so le trong)
Lại có: \(\widehat{{{A}_{1}}}+\widehat{{{B}_{2}}}={{180}^{0}}\) (hai góc trong cùng phía)
\(\Rightarrow \widehat{{{B}_{2}}}={{180}^{0}}-\widehat{{{B}_{1}}}={{180}^{0}}-{{100}^{0}}={{80}^{0}}\)
Chọn B
Câu hỏi 16 :
Cho hình vẽ sau:
Biết \(a\,//\,b,\,\widehat{{{A}_{1}}}-\widehat{{{C}_{1}}}={{40}^{0}}\). Tính \(\widehat{{{A}_{2}}},\,\widehat{{{C}_{2}}}\).
- A \(\widehat{{{A}_{2}}}={{60}^{0}}\) và \(\widehat{{{C}_{2}}}={{120}^{0}}\)
- B \(\widehat{{{A}_{2}}}={{80}^{0}}\) và \(\widehat{{{C}_{2}}}={{150}^{0}}\)
- C \(\widehat{{{A}_{2}}}={{70}^{0}}\) và \(\widehat{{{C}_{2}}}={{110}^{0}}\)
- D \(\widehat{{{A}_{2}}}={{90}^{0}}\) và \(\widehat{{{C}_{2}}}={{140}^{0}}\)
Đáp án: C
Phương pháp giải:
áp dụng tính chất của hai đường thẳng song song.
Lời giải chi tiết:
Vì \(a\,//\,b\left( gt \right)\Rightarrow \widehat{{{A}_{1}}}+\widehat{{{C}_{1}}}={{180}^{0}}\) (2 góc trong cùng phía bù nhau)
Mà lại có:
\(\begin{align} & \widehat{{{A}_{1}}}-\widehat{{{C}_{1}}}={{40}^{0}}\left( gt \right)\Rightarrow \widehat{{{A}_{1}}}=\left( {{180}^{0}}+{{40}^{0}} \right):2={{110}^{0}} \\ & \Rightarrow \widehat{{{C}_{1}}}={{110}^{0}}-{{40}^{0}}={{70}^{0}} \\\end{align}\)
Vì \(a\,//\,b\left( gt \right)\Rightarrow \left\{ \begin{align} & \widehat{{{A}_{1}}}=\widehat{{{C}_{2}}}={{110}^{0}} \\ & \widehat{{{C}_{1}}}=\widehat{{{A}_{2}}}={{70}^{0}} \\\end{align} \right.\)(2 góc so le trong)
Chọn C
Câu hỏi 17 :
Hải đường thẳng \(AB,CD\) cắt nhau
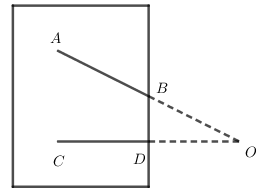
ở ngoài phạm vi của tờ giấy (xem hình minh họa).
Làm thế nào để biết được góc nhọn tạo bởi hai đường thẳng ấy?
Phương pháp giải:
Quan sát hình rồi tìm hướng giải quyết sao cho thỏa mãn đề bài.
Lời giải chi tiết:

Từ \(A\) kẻ tia \(Ax//CD\)
Khi đó: \(\angle BAx = \angle BOC\) (Hai góc so le trong, \({\rm{Ax}}//CD\)
Vậy góc nhọn tạo bởi 2 đường thẳng \(AB,CD\) có số đo
bằng số đo của \(\angle BAx\)
Câu hỏi 18 :
Cho hình vẽ bên. Biết \(a//b\) và \(\angle {B_1} = {60^0}.\)
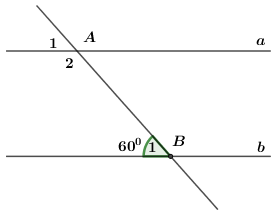
Tính \(\angle {A_1},\,\angle {A_2}.\)
- A \(\angle {A_1} = {60^0};\,\,\,\angle {A_2} = {90^0}\)
- B \(\angle {A_1} = {90^0};\,\,\,\angle {A_2} = {120^0}\)
- C \(\angle {A_1} = {120^0};\,\,\,\angle {A_2} = {60^0}\)
- D \(\angle {A_1} = {60^0};\,\,\,\angle {A_2} = {120^0}\)
Đáp án: D
Phương pháp giải:
Dựa vào tính chất của hai đường thẳng song song:
Nếu một đường thẳng cắt hai đường thẳng song song thì:
+ Hai góc so le trong bằng nhau;
+ Hai góc đồng vị bằng nhau;
+ Hai góc trong cùng phía bù nhau;
Lời giải chi tiết:

Biết \(a//b\) và \(\angle {B_1} = {60^0}.\)
Quan sát hình đã cho, ta thấy, \({A_1} = {B_1}\, = {60^0}\,\,\left( {so\,le\,trong} \right)\).
\(\angle {A_2}\) và góc \(\angle {B_1}\) là hai góc ở vị trí trong cùng phía, do đó\(\angle {A_2} + \angle {B_1} = {180^0} \Rightarrow \angle {A_2} = {180^0} - \angle {B_1} = {180^0} - {60^0} = {120^0}\)
Vậy \(\angle {A_1} = {60^0};\,\,\,\angle {A_2} = {120^0}\)
Chọn D
Câu hỏi 19 :
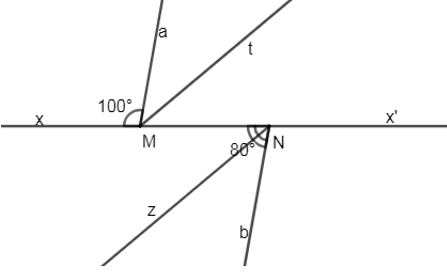
a) Cho hình vẽ. Biết \(Bx//Oz,\,Oz//Ny\) và \(\widehat {xBO} = 130^\circ ,\widehat {ONy} = 140^\circ .\) Tính \(\widehat {NOB}.\)

b) Cho \(5\) đường thẳng phân biệt sao cho không có \(2\) đường thẳng nào song song. Chứng minh tồn tại một cặp đường thẳng tạo với nhau một góc không quá \(36^\circ .\)
Phương pháp giải:
a) Vận dụng kiến thức: Khi một đường thẳng cắt hai đường thẳng song song thì tạo thành các cặp góc so le trong bằng nhau, các cặp góc đồng vị bằng nhau hoặc các cặp góc trong cùng phía bù nhau.
b) Lấy một điểm \(O\) bất kì trong mặt phẳng, qua \(O\) dựng các đường thẳng song song với các đường thẳng đã cho.
Chứng minh bằng phản chứng, giả sử các góc tạo thành đều lớn hơn \({36^0}\) suy ra điều mâu thuẫn và kết luận.
Lời giải chi tiết:
a) Cho hình vẽ. Biết \(Bx//Oz,\,Oz//Ny\) và \(\widehat {xBO} = 130^\circ ,\widehat {ONy} = 140^\circ .\) Tính \(\widehat {NOB}.\)

Ta có \(Bx//Oz;\,Oz//Ny\) nên
Vẽ tia \(Oz'\) là tia đối của tia \(Oz\)
Ta có \(Oz'//Bx\) nên \(\widehat {xBO} + \widehat {{O_1}} = 180^\circ \) (hai góc trong cùng phía)
Mà \(\widehat {xBO} = 130^\circ \) nên \(\widehat {{O_1}} = 180^\circ - 130^\circ = 50^\circ \)
Chứng minh tương tự ta có \(\widehat {ONy} + \widehat {{O_2}} = 180^\circ \) (do \(Oz'//Ny\))
mà \(\widehat {ONy} = 140^\circ \) nên \(\widehat {{O_2}} = 180^\circ - 140^\circ = 40^\circ \)
Tia \(Oz'\) chia góc \(NOB\) thành hai góc \({O_1}\) và góc \({O_2}\) nên \(\widehat {NOB} = \widehat {{O_1}} + \widehat {{O_2}} = 50^\circ + 40^\circ = 90^\circ \)
b) Cho \(5\) đường thẳng phân biệt sao cho không có \(2\) đường thẳng nào song song. Chứng minh tồn tại một cặp đường thẳng tạo với nhau một góc không quá \(36^\circ .\)
Lấy một điểm \(O\) bất kì, qua \(O\) kẻ các đường thẳng song song với \(5\) đường thẳng đã cho.
Khi đó tạo thành \(10\) góc tại \(O\) có tổng số đo bằng \({360^0}\), trong đó có \(5\) cặp góc đối đỉnh \(\widehat {{O_1}} = \widehat {{O_6}},\widehat {{O_2}} = \widehat {{O_7}},\widehat {{O_3}} = \widehat {{O_8}},\) \(\widehat {{O_4}} = \widehat {{O_9}},\widehat {{O_5}} = \widehat {{O_{10}}}\) nên:
\(\widehat {{O_1}} + \widehat {{O_2}} + \widehat {{O_3}} + \widehat {{O_4}} + \widehat {{O_5}}\)\( = \widehat {{O_6}} + \widehat {{O_7}} + \widehat {{O_8}} + \widehat {{O_9}} + \widehat {{O_{10}}} = \frac{{{{360}^0}}}{2} = {180^0}\)
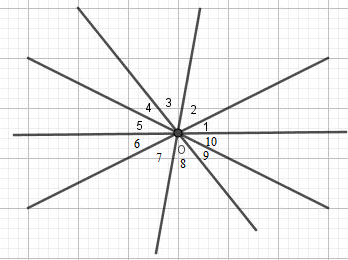
Giả sử không tồn tại cặp đường thẳng nào tạo với nhau một góc không quá \({36^0}\) hay tất cả các góc tạo thành đều lớn hơn \({36^0}\).
Khi đó \(\widehat {{O_1}} > {36^0},\widehat {{O_2}} > {36^0},\widehat {{O_3}} > {36^0},\widehat {{O_4}} > {36^0},\widehat {{O_5}} > {36^0}\)
\( \Rightarrow \widehat {{O_1}} + \widehat {{O_2}} + \widehat {{O_3}} + \widehat {{O_4}} + \widehat {{O_5}} > {36^0} + {36^0} + {36^0} + {36^0} + {36^0} = {180^0}\)
(mâu thuẫn vì \(\widehat {{O_1}} + \widehat {{O_2}} + \widehat {{O_3}} + \widehat {{O_4}} + \widehat {{O_5}} = {180^0}\))
Vậy phải tồn tại một cặp đường thẳng tạo với nhau một góc không quá \({36^0}\).
Câu hỏi 20 :
Chọn câu đúng.
- A Qua điểm A nằm ngoài đường thẳng m, có vô số đường thẳng song song với m.
- B Qua điểm A nằm ngoài đường thẳng m, có duy nhất một đường thẳng song song với m.
- C Qua điểm A nằm ngoài đường thẳng d, có hai đường thẳng phân biệt cùng song song với D.
- D Nếu hai đường thẳng AB và AC cùng song song với đường thẳng d thì hai đường thẳng AB và AC song song với nhau.
Đáp án: B
Phương pháp giải:
Sử dụng tiên đề Ơ-clit về hai đường thẳng song song
Lời giải chi tiết:
Tiên đề Ơ-clit: “Qua một điểm nằm ngoài một đường thẳng, chỉ có một đường thẳng song song song với đường thẳng đó.”
Chọn B.
Câu hỏi 21 :
Trong số các câu sau có bao nhiêu câu đúng?
Nếu một đường thẳng cắt một trong hai đường thẳng song song thì:
(I) Hai góc đồng vị bằng nhau;
(II) Hai góc so le ngoài bằng nhau;
(III) Hai góc trong cùng phía bù nhau;
(IV) Hai góc so le trong bằng nhau.
- A \(1\)
- B \(2\)
- C \(3\)
- D \(4\)
Đáp án: D
Phương pháp giải:
Áp dụng tính chất hai đường thẳng song song.
Lời giải chi tiết:
Nếu hai đường thẳng song song bị cắt bởi một đường thẳng thứ ba thì:
+ Hai góc so le trong còn lại bằng nhau, hai góc so le ngoài bằng nhau.
+ Hai góc đồng vị bằng nhau
+ Hai góc trong cùng phía bù nhau
Nên cả (I), (II), (III), (IV) đều đúng.
Chọn D.
Câu hỏi 22 :
Cho hình vẽ sau:
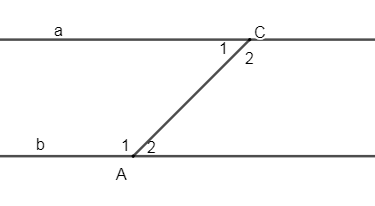
Biết \(a\,//\,b,\,\widehat {{A_1}} - \widehat {{C_1}} = {40^0}\). Tính \(\widehat {{A_2}},\,\widehat {{C_2}}\).
- A \(\widehat {{A_2}} = 80^\circ ;\,\widehat {{C_2}} = 110^\circ \)
- B \(\widehat {{A_2}} = 110^\circ ;\,\widehat {{C_2}} = 70^\circ \)
- C \(\widehat {{A_2}} = 70^\circ ;\,\widehat {{C_2}} = 110^\circ \)
- D \(\widehat {{A_2}} = 70^\circ ;\,\widehat {{C_2}} = 70^\circ \)
Đáp án: C
Phương pháp giải:
áp dụng tính chất của hai đường thẳng song song.
Lời giải chi tiết:
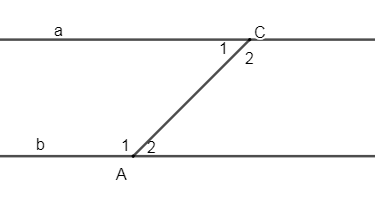
Vì \(a\,//\,b\left( {gt} \right) \Rightarrow \widehat {{A_1}} + \widehat {{C_1}} = {180^0}\) (2 góc trong cùng phía bù nhau)
Mà lại có:
\(\begin{array}{l}\widehat {{A_1}} - \widehat {{C_1}} = {40^0}\left( {gt} \right) \Rightarrow \widehat {{A_1}} = \left( {{{180}^0} + {{40}^0}} \right):2 = {110^0}\\ \Rightarrow \widehat {{C_1}} = {110^0} - {40^0} = {70^0}\end{array}\)
Vì \(a\,//\,b\left( {gt} \right) \Rightarrow \left\{ \begin{array}{l}\widehat {{A_1}} = \widehat {{C_2}} = {110^0}\\\widehat {{C_1}} = \widehat {{A_2}} = {70^0}\end{array} \right.\)(2 góc so le trong)
Vậy \(\widehat {{A_2}} = 70^\circ ;\,\widehat {{C_2}} = 110^\circ .\)
Chọn C
Câu hỏi 23 :
Cho hình vẽ sau, biết \(a//b\) và \(\widehat {{A_1}} = {100^0}\). Tính \(\widehat {{B_1}},\widehat {{B_2}}\).
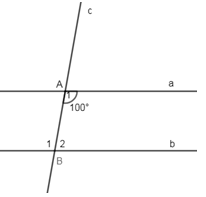
- A \(\widehat {{B_1}} = \widehat {{B_2}} = {100^0}\)
- B \(\widehat {{B_1}} = {100^0},\,\,\widehat {{B_2}} = {80^0}\)
- C \(\widehat {{B_1}} = {80^0},\,\,\widehat {{B_2}} = {100^0}\)
- D \(\widehat {{B_1}} = {100^0},\,\,\widehat {{B_2}} = {90^0}\)
Đáp án: B
Phương pháp giải:
Áp dụng tính chất của hai đường thẳng song song.
Lời giải chi tiết:
Vì \(a//b\left( {gt} \right) \Rightarrow \widehat {{A_1}} = \widehat {{B_1}}\, = {100^0}\) (hai góc so le trong)
Lại có: \(\widehat {{A_1}} + \widehat {{B_2}} = {180^0}\) (hai góc trong cùng phía)
\( \Rightarrow \widehat {{B_2}} = {180^0} - \widehat {{B_1}} = {180^0} - {100^0} = {80^0}.\)
Chọn B.
Câu hỏi 24 :
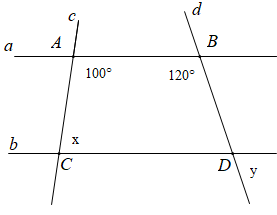
Cho hình vẽ sau:
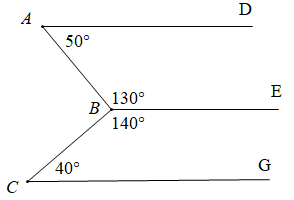
Chọn câu đúng.
- A \(AD//BE\)
- B \(BE//CG\)
- C Cả A, B đều sai
- D Cả A, B đều đúng.
Đáp án: D
Phương pháp giải:
Áp dụng tiên đề Ơ-clit, tính chất hai đường thẳng song song.
Lời giải chi tiết:
Vì \(\widehat A + \widehat {ABE} = 50^\circ + 130^\circ = 180^\circ \) mà hai góc ở vị trí trong cùng phía nên \(AD//BE.\)
Vì \(\widehat {CBE} + \widehat C = 140^\circ + 40^\circ = 180^\circ \) mà hai góc ở vị trí trong cùng phía nên \(BE//CG.\)
Vậy cả A, B đều đúng.
Chọn D.
Câu hỏi 25 :
Trên đường thẳng xx’ lấy hai điểm M và N. Trên hai nửa mặt phẳng đối nhau bờ là xx’ dựng các tia Ma, Nb sao cho \(\widehat{xMa}={{100}^{0}},\,\widehat{bN\text{x}}={{80}^{0}}\).
a) Chứng minh \(Ma\,//\,Nb\).
b) Gọi Mt và Nz lần lượt là tia phân giác của \(\widehat{aMx'}\) và \(\widehat{xNb}\). Tia Mt có song song với tia Nz không? Vì sao?
Phương pháp giải:
Áp dụng dấu hiệu nhận biết hai đường thẳng song song, tính chất tia phân giác.
Lời giải chi tiết:
a) Ta có: \(\widehat{xMa}+\widehat{aMx'}={{180}^{0}}\) (kề bù)
\(\Rightarrow \widehat{aMx'}={{180}^{0}}-{{100}^{0}}={{80}^{0}}\Rightarrow \widehat{aMx'}=\widehat{xNb}\left( ={{80}^{0}} \right)\)
Mà 2 góc đó ở vị trí so le trong nên suy ra \(Ma\,//\,Nb\).
b) Vì Mt là tia phân giác của \(\widehat{aMx'}\left( gt \right)\Rightarrow \widehat{tMx'}=\frac{\widehat{aMx'}}{2}={{80}^{0}}:2={{40}^{0}}\) (tính chất tia phân giác)
Vì Nz là tia phân giác của \(\widehat{xNb}\left( gt \right)\Rightarrow \widehat{xNz}=\frac{\widehat{xNb}}{2}={{80}^{0}}:2={{40}^{0}}\) (tính chất tia phân giác)
Mà 2 góc \(\widehat{tMx'}\) và \(\widehat{xNz}\) là hai góc ở vị trí so le trong nên \(\Rightarrow Mt//N\text{z}\)(dấu hiệu nhận biết hai đường thẳng song song)
>> Học trực tuyến lớp 7 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 7 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
 |
 |
 |
 |
 |
 |
Các bài khác cùng chuyên mục