25 bài tập đường thẳng song song với mặt phẳng mức độ nhận biết
Làm đề thiCâu hỏi 1 :
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB và AC. Khi đó:
- A MN//(BCD)
- B MN cắt (BCD)
- C MN//(ABD)
- D MN//(ABC)
Đáp án: A
Lời giải chi tiết:
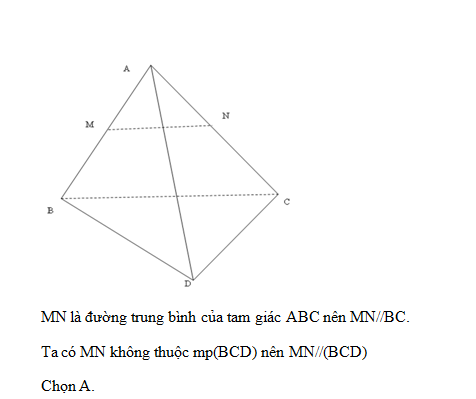
Câu hỏi 2 :
Cho hình lập phương ABCD.A’B’C’D’. Khi đó AC song song với mặt phẳng nào:
- A (ACC’A’)
- B (A’B’C’D’)
- C (BDB’D’)
- D (ADA’D’)
Đáp án: B
Lời giải chi tiết:
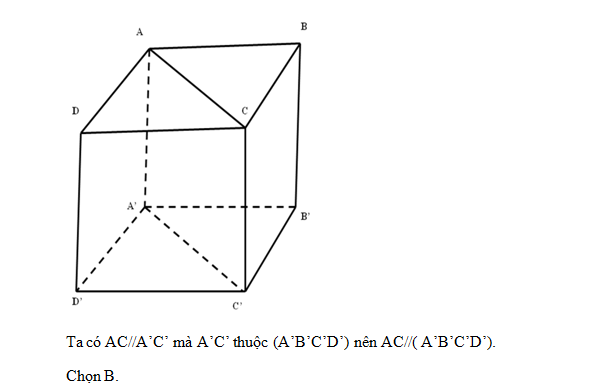
Câu hỏi 3 :
Cho hình lập phương ABCD.A’B’C’D’, I và J là tâm của hai hình vuông ABCD và ABB’A’. Khi đó:
- A IJ//( A’B’C’D’)
- B IJ//(ABCD)
- C IJ//(ABB’A’)
- D IJ//(A’B’CD)
Đáp án: D
Lời giải chi tiết:
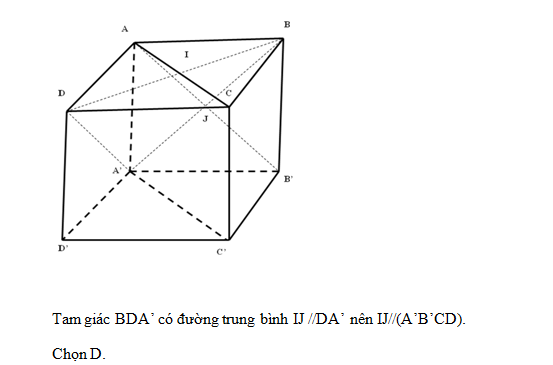
Câu hỏi 4 :
Cho tứ diện ABCD có I và J lần lượt là trọng tâm của tam giác ABC và ABD. Đường thẳng IJ song song với đường thẳng:
- A CM trong đó M là trung điểm của BD
- B AC
- C DB
- D CD
Đáp án: D
Phương pháp giải:
Đưa về cùng mặt phẳng và vận dụng các kiến thức hình học phẳng
Lời giải chi tiết:
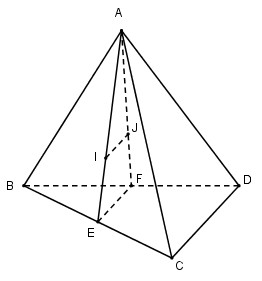
Gọi E, F lần lượt là trung điểm của BC và BD ta có:
\(\eqalign{ & I \in AE\,;\,{{AI} \over {AE}} = {2 \over 3} \cr & J \in AF\,;\,{{AJ} \over {AF}} = {2 \over 3} \cr} \)
Xét trong mp(AEF) ta suy ra IJ // EF (Định lí Ta – let đảo)
Mà EF là đường trung bình của tam giác BCD nên EF // CD
Vậy IJ // CD.
Chọn D.
Câu hỏi 5 :
Cho tứ diện ABCD, gọi G là trọng tâm tam giác ACD, M thuộc đoạn thẳng BC sao cho CM = 2MB. Chọn mệnh đề đúng trong các mệnh đề sau?
- A MG // (ABC)
- B MG // (ABD)
- C MG // CD
- D MG // BD
Đáp án: B
Phương pháp giải:
- Đưa về cùng một mặt phẳng.
- Sử dụng tính chất trọng tâm của tam giác.
- Áp dụng định lí Ta – let đảo để chứng minh hai đường thẳng song song.
Lời giải chi tiết:
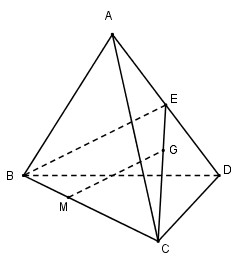
Gọi E là trung điểm của AD ta có \(G \in CE\) và \({{CG} \over {CE}} = {2 \over 3}\)
Vì \(CM = 2MB \Rightarrow {{CM} \over {CB}} = {2 \over 3}\)
Xét tam giác BCE có: \({{CG} \over {CE}} = {{CM} \over {CB}} = {2 \over 3} \Rightarrow \) MG // BE (Định lí Ta – let đảo)
Mà \(BE \subset \left( {ABD} \right) \Rightarrow \) MG // (ABD)
Chọn B.
Câu hỏi 6 :
Tìm mệnh đề đúng trong các mệnh đề sau:
- A Hai đường thẳng phân biệt nếu không có điểm chung thì song song.
- B Hai đường thẳng phân biệt nếu không có điểm chung thì chéo nhau.
- C Hai đường thẳng phân biệt không cắt nhau thì song song.
- D Hai đường thẳng phân biệt nếu không có điểm chung thì chéo nhau hoặc song song.
Đáp án: D
Phương pháp giải:
Sử dụng định nghĩa về hai đường thẳng song song và chéo nhau.
Lời giải chi tiết:
Chọn D.
Câu hỏi 7 :
Cho hình chóp S.ABCD. Gọi M, N lần lượt là trọng tâm của tam giác SAB và ABC. Khi đó MN song song với
- A mp(SAD)
- B AD
- C mp(SCD)
- D mp(SBD)
Đáp án: C
Phương pháp giải:
- Đưa về cùng một mặt phẳng.
- Sử dụng tính chất trọng tâm của tam giác.
- Áp dụng định lí Ta – let đảo để chứng minh hai đường thẳng song song.
Lời giải chi tiết:
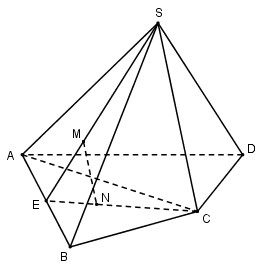
Gọi E là trung điểm của AB ta có:
\(\eqalign{ & M \in SE\,;\,{{EM} \over {ES}} = {1 \over 3} \cr & N \in EC\,;\,{{EN} \over {EC}} = {1 \over 3} \cr} \)
Xét tam giác ESC ta có \({{EM} \over {ES}} = {{EN} \over {EC}} = {1 \over 3} \Rightarrow \) MN // SC (Định lí Ta – let đảo).
Mà \(SC \subset \left( {SCD} \right) \Rightarrow \)MN // (SCD)
Chọn C.
Câu hỏi 8 :
Hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng. Gọi O và O’ lần lượt là tâm hình bình hành ABCD và ABEF. OO’ song song với:
- A mp(DCEF)
- B mp(ADF)
- C mp(BCE)
- D Cả A, B, C
Đáp án: D
Phương pháp giải:
- Sử dụng tính chất của tâm hình bình hành.
- Áp dụng định lí Ta – let đảo để chứng minh các đường thẳng song song.
Lời giải chi tiết:
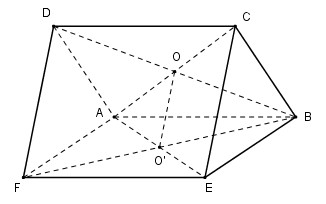
Vì O và O’ lần lượt là tâm hình bình hành ABCD và ABEF nên O là trung điểm của BD; O’ là trung điểm của FB.
Xét tam giác BDF có: OO’ là đường trung bình \( \Rightarrow \) OO’ // DF
Mà \(DF \subset \left( {DCEF} \right);\,DF \subset \left( {ADF} \right)\,;\,DF\parallel \left( {BCE} \right)\,\,\left( {DF\parallel CE} \right)\)
Nên OO’ // (DCEF) ; OO’ // (ADF) ; OO’ // (BCE)
Chọn D.
Câu hỏi 9 :
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P, Q lần lượt là các điểm nằm trên các cạnh BC, SC, SD, AD sao cho MN / BS, NP // CD, MQ // CD. Hỏi PQ song song với mặt phẳng nào sau đây?
- A mp(SBC)
- B mp(SAB)
- C mp(SAD)
- D mp(SCD)
Đáp án: B
Phương pháp giải:
- Sử dụng định lí Ta – let thuận và Ta – let đảo.
Lời giải chi tiết:
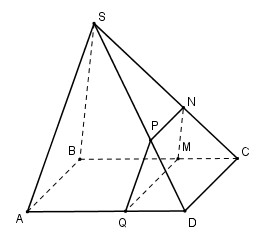
Vì MN // BS nên \({{CN} \over {CS}} = {{CM} \over {CB}}\) (Định lí Ta – let) (1)
Vì MQ // CD // AB nên \({{CM} \over {CB}} = {{DQ} \over {DA}}\) (2)
Vì NP // CD nên \({{CN} \over {CS}} = {{DP} \over {DS}}\)(Định lí Ta – let) (3)
Từ (1), (2) và (3) suy ra \({{DP} \over {DS}} = {{DQ} \over {DA}} \Rightarrow \) PQ // SA (Định lí Ta – let đảo)
Ta có: \(SA \subset \left( {SAB} \right)\,\,;\,\,SA \subset \left( {SAD} \right)\). Tuy nhiên \(PQ \subset \left( {SAD} \right)\) nên PQ không song song với mp(SAD).
Vậy PQ // (SAB).
Chọn B.
Câu hỏi 10 :
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi d là giao tuyến của hai mặt phẳng (SAD) và (SBC). Khẳng định nào sau đây là đúng?
- A d qua S và song song với BC.
- B d qua S và song song với DC
- C d qua S và song song với AB.
- D d qua S và song song với BD.
Đáp án: A
Phương pháp giải:
Sử dụng tính chất: Nếu hai mặt phẳng và có điểm chung M và lần lượt chứa hai đường thẳng song song d và d’ thì giao tuyến của và là đường thẳng đi qua M và song song với d và d’.
Lời giải chi tiết:
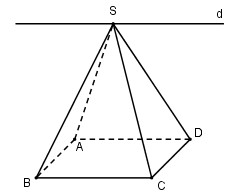
Ta có: \(\left\{ \matrix{AD \subset \left( {SAD} \right) \hfill \cr BC \subset \left( {SBC} \right) \hfill \cr AD//BC \hfill \cr d = \left( {SAD} \right) \cap \left( {SBC} \right) \hfill \cr} \right. \Rightarrow d//AD//BC\)
Chọn A.
Câu hỏi 11 :
Cho hình chóp S.ABCD có đáy ABCD là hình thang đáy lớn AB. Gọi M là một điểm trên cạnh CD; \(\left( \alpha \right)\) là mặt phẳng qua M và song song với SA và BC. Thiết diện của mp \(\left( \alpha \right)\) với hình chóp là:
- A Hình tam giác
- B Hình thang.
- C Hình bình hành
- D Hình chữ nhật
Đáp án: B
Phương pháp giải:
- Đưa về cùng mặt phẳng.
- Sử dụng tính chất: Nếu hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) có điểm chung M và lần lượt chứa hai đường thẳng song song d và d’ thì giao tuyến của \(\left( \alpha \right)\) và \(\left( \beta \right)\) là đường thẳng đi qua M và song song với d và d’.
Lời giải chi tiết:
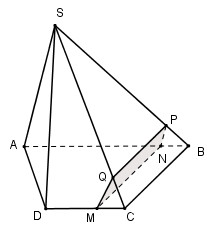
Ta có: \(\left\{ \matrix{M \in \left( \alpha \right) \cap \left( {ABCD} \right) \hfill \cr BC\parallel \left( \alpha \right) \hfill \cr BC \subset \left( {ABCD} \right) \hfill \cr} \right. \Rightarrow \left( \alpha \right) \cap \left( {ABCD} \right) = MN\parallel BC\,\left( {N \in AB} \right)\,\,\left( 1 \right).\)
Tương tự:
\(\eqalign{ & \left\{ \matrix{N \in \left( \alpha \right) \cap \left( {SAB} \right) \hfill \cr SA\parallel \left( \alpha \right) \hfill \cr SA \subset \left( {SAB} \right) \hfill \cr} \right. \Rightarrow \left( \alpha \right) \cap \left( {SAB} \right) = NP\parallel SA\,\left( {P \in SB} \right) \cr & \left\{ \matrix{P \in \left( \alpha \right) \cap \left( {SBC} \right) \hfill \cr BC\parallel \left( \alpha \right) \hfill \cr BC \subset \left( {SBC} \right) \hfill \cr} \right. \Rightarrow \left( \alpha \right) \cap \left( {SBC} \right) = PQ\parallel BC\,\left( {Q \in SC} \right)\,\,\left( 2 \right). \cr} \)
Từ (1) và (2) suy ra MN // PQ.
Vậy thiết diện là hình thang MNPQ.
Chọn B.
Câu hỏi 12 :
Cho hình lập phương ABCD.A’B’C’D’, AC và BD cắt nhau tại O, A’C’ và B’D’ cắt nhau tại O’. Các điểm M, N, P theo thứ tự là trung điểm của AB, BC, O'B’. Khi đó thiết diện do mặt phẳng (MNP) cắt hình lập phương sẽ là đa giác có số cạnh là bao nhiêu?
- A 3
- B 4
- C 5
- D 6
Đáp án: B
Phương pháp giải:
Sử dụng tính chất: Nếu hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) có điểm chung M và lần lượt chứa hai đường thẳng song song d và d’ thì giao tuyến của \(\left( \alpha \right)\) và \(\left( \beta \right)\) là đường thẳng đi qua M và song song với d và d’.
Lời giải chi tiết:
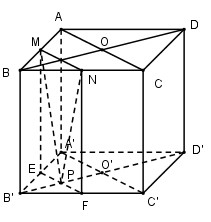
Ta có: MN là đường trung bình của tam giác ABC nên MN // AC // A’C’.
(MNP) và (A’B’C’D’) có điểm P chung và MN // A’C’.
Qua P kẻ EF // A’C’ \(E \in A'B',F \in B'C'.\)
Vậy thiết diện của hình lập phương cắt bởi mp(MNP) là MNFE.
Chọn B.
Câu hỏi 13 :
Trong các mệnh đề sau, mệnh đề nào đúng?
- A Hai mặt phẳng phân biệt cùng song song với mặt phẳng thứ ba thì song song với nhau.
- B Ba mặt phẳng cắt nhau theo giao tuyến phân biệt thì 3 giao tuyến đó đồng quy.
- C Cho 2 đường thẳng chéo nhau, không tồn tại mặt phẳng nào qua đường thẳng này và song song với đường thẳng kia.
- D Cho hai mặt phẳng song song, đường thẳng nào cắt mặt phẳng này thì không cắt mặt phẳng kia.
Đáp án: A
Phương pháp giải:
Dùng các kiến thức liên quan đến đường thẳng và mặt phẳng song song.
Lời giải chi tiết:
B sai vì Ba mặt phẳng cắt nhau theo giao tuyến phân biệt thì 3 giao tuyến đó đồng quy hoặc song song.
C sai Cho 2 đường thẳng chéo nhau, tồn tại mặt phẳng nào qua đường thẳng này và song song với đường thẳng kia.
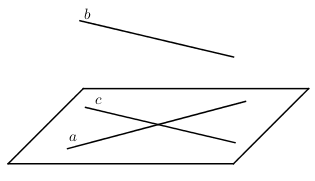
a và b chéo nhau, tồn tại mặt phẳng chứa a và song song với b.
D sai.
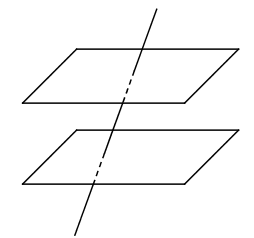
Chọn A.
Câu hỏi 14 :
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi I, J lần lượt là trung điểm của AB và BC. Khi đó giao tuyến của hai mặt phẳng (SAB) và (SCD) là đường thẳng song song với:
- A BJ
- B AD
- C BI
- D IJ
Đáp án: C
Phương pháp giải:
Sử dụng tính chất: Nếu hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) có điểm chung M và lần lượt chứa hai đường thẳng song song d và d’ thì giao tuyến của \(\left( \alpha \right)\) và \(\left( \beta \right)\) là đường thẳng đi qua M và song song với d và d’.
Lời giải chi tiết:
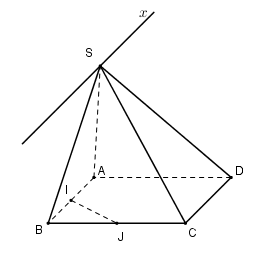
(SAB) và (SCD) có điểm S chung.
\(\left. \begin{array}{l}\left( {SAB} \right) \supset AB\\\left( {SCD} \right) \supset CD\\AB\parallel CD\end{array} \right\} \Rightarrow \)Giao tuyến của (SAB) và (SCD) là đường thẳng Sx // AB // CD.
Sx // BI.
Chọn C.
Câu hỏi 15 :
Cho hinh chóp S.ABCD có ABCD là hình bình hành tâm O, I là trung diểm của cạnh SC. Khẳng định nào sau đây sai ?
- A
Giao tuyến của hai mặt phẳng \(\left( IBD \right)\) và \(\left( SAC \right)\) là IO.
- B
Đường thẳng IO song song với mặt phẳng \(\left( SAB \right)\).
- C
Mặt phẳng \(\left( IBD \right)\) cắt hình chóp \(S.ABCD\) theo thiết diện là 1 tứ giác.
.
- D Đường thẳng IO song song với mặt phẳng \(\left( SAD \right)\)
Đáp án: C
Phương pháp giải:
Suy luận từng đáp án.
Lời giải chi tiết:
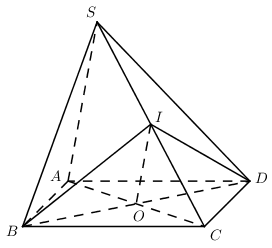
A đúng.
Ta có IO // SA \(\Rightarrow IO//\left( SAB \right)\) và \(IO//\left( SAD \right)\Rightarrow B,D\) đúng.
Mặt phẳng \(\left( IBD \right)\) cắt hình chóp \(S.ABCD\) theo thiết diện chính là tam giác IBD. C sai.
Chọn C.
Câu hỏi 16 :
Cho hai đường thẳng song song a và b. Có bao nhiêu mặt phẳng chứa a và song song với b?
- A 1
- B vô số
- C 0
- D 2
Đáp án: B
Lời giải chi tiết:
Hai đường thẳng a và b song song với nhau \( \Rightarrow \) Có vô số mặt phẳng chứa a và song song với b (đó là tất cả các mặt phẳng chứa a nhưng không chứa b).
Chọn: B
Câu hỏi 17 :
Cho mặt phẳng (P) và điểm A không thuộc (P). Số đường thẳng qua A song song (P) là:
- A 0.
- B 1.
- C 2.
- D Vô số.
Đáp án: D
Lời giải chi tiết:
Có vô số đường thẳng qua A song song (P).
Chọn: D
Câu hỏi 18 :
Trong các khẳng định sau, khẳng định nào đúng?
- A Nếu hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của chúng (nếu có) cùng song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.
- B Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến thì ba giao tuyến ấy hoặc đổng quy hoặc đôi một song song.
- C Nếu hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của chúng (nếu có) cũng song song với hai đường thẳng đó.
- D Hai đường thẳng cùng song song với một đường thẳng thứ ba thì song song với nhau.
Đáp án: A
Lời giải chi tiết:
Khẳng định đúng là: Nếu hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của chúng (nếu có) cùng song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.
Chọn: A
Câu hỏi 19 :
Cho đường thẳng a song song với mặt phẳng \(\left( \alpha \right)\). Nếu \(\left( \beta \right)\) chứa a và cắt \(\left( \alpha \right)\) theo giao tuyến b thì b và a là hai đường thẳng :
- A cắt nhau.
- B trùng nhau.
- C chéo nhau.
- D song song với nhau.
Đáp án: D
Lời giải chi tiết:
Cho đường thẳng a song song với mặt phẳng \(\left( \alpha \right)\). Nếu \(\left( \beta \right)\) chứa a và cắt \(\left( \alpha \right)\) theo giao tuyến b thì b và a là hai đường thẳng song song với nhau.
Chọn: D
Câu hỏi 20 :
Cho hình chóp S.ABCD có đáy ABCD là hình thang, đáy lớn AB. Gọi P, Q lần lượt là hai điểm nằm trên SA và SB sao cho \(\dfrac{{SP}}{{SA}} = \dfrac{{SQ}}{{SB}} = \dfrac{1}{3}\). Khẳng định nào sau đây là đúng?
- A PQ cắt (ABCD)
- B \(PQ \subset \left( {ABCD} \right)\)
- C \(PQ//\left( {ABCD} \right)\)
- D PQ và CD chéo nhau
Đáp án: C
Phương pháp giải:
Một đường thẳng (d) song song với mặt phẳng (P) nếu (d) song song với một đường thẳng trong (P).
Lời giải chi tiết:
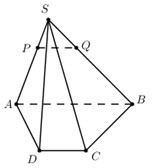
Ta có \(\dfrac{{SP}}{{SA}} = \dfrac{{SQ}}{{SB}} = \dfrac{1}{3} \Rightarrow PQ//AB.\) Mà \(AB \subset \left( {ABCD} \right) \Rightarrow PQ//\left( {ABCD} \right)\).
Chọn C.
Câu hỏi 21 :
Cho mặt phẳng \(\left( \alpha \right)\) và đường thẳng \(d \not\subset \left( \alpha \right)\). Khẳng định nào sau đây SAI?
- A Nếu d song song với \(\left( \alpha \right)\) thì trong mặt phẳng \(\left( \alpha \right)\) tồn tại đường thẳng d’ song song với d.
- B Nếu d song song với \(\left( \alpha \right)\) và đường thẳng \(d' \subset \left( \alpha \right)\) thì d’ song song với d.
- C Nếu d song song với \(d'\) và đường thẳng \(d' \subset \left( \alpha \right)\) thì d song song với \(\left( \alpha \right)\) .
- D Nếu d cắt mặt phẳng \(\left( \alpha \right)\) tại A và d’ là một đường thẳng bất kì trong \(\left( \alpha \right)\) thì d và d’ hoặc cắt nhau hoặc chéo nhau.
Đáp án: B
Lời giải chi tiết:
Khẳng định SAI là: Nếu d song song với \(\left( \alpha \right)\) và đường thẳng \(d' \subset \left( \alpha \right)\) thì d’ song song với d.
Chọn: B
Câu hỏi 22 :
Trong không gian, đường thẳng \(a\) song song với mặt phẳng \(\left( P \right)\) nếu
- A \(\left\{ \begin{array}{l}a//b\\b \not\subset \left( P \right)\end{array} \right.\)
- B \(a \not\subset \left( P \right)\)
- C \(\left\{ \begin{array}{l}a//b\\b \subset \left( P \right)\\a \not\subset \left( P \right)\end{array} \right.\)
- D \(\left\{ \begin{array}{l}a//b\\b \subset \left( P \right)\end{array} \right.\)
Đáp án: C
Phương pháp giải:
Sử dụng điều kiện đường thẳng song song mặt phẳng nếu nó không nằm trong mặt phẳng và song song với một đường thẳng nằm trong mặt phẳng đó
Lời giải chi tiết:
Đường thẳng \(a\) song song mặt phẳng \(\left( P \right)\) nếu \(\left\{ \begin{array}{l}a//b\\b \subset \left( P \right)\\a \not\subset \left( P \right)\end{array} \right.\).
Chọn C
Câu hỏi 23 :
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Gọi \(M,\,\,N,\,\,K\) lần lượt là trung điểm của \(CD,\,\,CB,\,\,SA\). Mệnh đề nào sau đây đúng?
- A \(BD\parallel \left( {MNK} \right)\)
- B \(SB\parallel \left( {MNK} \right)\)
- C \(SC\parallel \left( {MNK} \right)\)
- D \(SD\parallel \left( {MNK} \right)\)
Đáp án: A
Phương pháp giải:
\(d\parallel a \subset \left( P \right) \Rightarrow d\parallel \left( P \right)\).
Lời giải chi tiết:
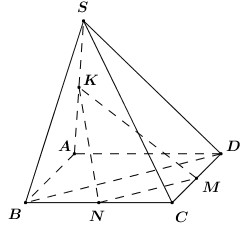
\(MN\) là đường trung bình của \(\Delta BCD \Rightarrow MN\parallel BD\).
Mà \(MN \subset \left( {MNK} \right) \Rightarrow BD\parallel \left( {MNK} \right)\).
Chọn A.
Câu hỏi 24 :
Trong các mệnh đề sau, mệnh đề nào sai ?
- A Nếu hai mặt phẳng phân biệt cùng song song với mặt phẳng thứ ba thì chúng song song với nhau.
- B Nếu hai mặt phẳng phân biệt cùng song song với một đường thẳng thì giao tuyến của chúng cũng song song với đường thẳng đó.
- C Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng còn vô số điểm chung khác nữa.
- D Nếu hai đường thẳng phân biệt cùng song song với một mặt phẳng thì song song với nhau.
Đáp án: D
Phương pháp giải:
Sử dụng tính chất song song trong không gian.
Lời giải chi tiết:
Câu D sai vì hai đường thẳng phân biệt song song với cùng một mặt phẳng thì chúng song song hoặc chéo nhau.
Chọn D.
Câu hỏi 25 :
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Gọi \(d\) là giao tuyến của hai mặt phẳng \(\left( {SAD} \right)\) và \(\left( {SBC} \right)\). Khẳng định nào sau đây đúng?
- A \(d\) qua \(S\) và song song với\(AC\).
- B \(d\) qua \(S\)và song song với\(AD\).
- C \(d\) qua \(S\) và song song với\(AB\).
- D \(d\) qua \(S\) và song song với\(BD\).
Đáp án: B
Phương pháp giải:
Dựng giao tuyến dựa vào yếu tố song song : \(\left\{ \begin{array}{l}a\parallel b\\a \subset \left( \alpha \right),\,b \subset \left( \beta \right)\\\left( \alpha \right) \cap \left( \beta \right) = d\end{array} \right. \Rightarrow d\parallel a\parallel b\)
Lời giải chi tiết:
\(\left\{ \begin{array}{l}AD\parallel BC\,\,\left( {gt} \right)\\AD \subset \left( {SAD} \right),\,BC \subset \left( {SBC} \right)\\\left( {SAD} \right) \cap \left( {SBC} \right) = d\\S \in \left( {SAD} \right) \cap \left( {SBC} \right)\end{array} \right. \Rightarrow d\)qua \(S\)và song song với \(AD,\,\,BC\).
Chọn: B.
Tổng hợp các bài tập trắc nghiệm đường thẳng song song với mặt phẳng mức độ thông hiểu có đáp án và lời giải chi tiết
Tổng hợp các bài tập trắc nghiệm đường thẳng song song với mặt phẳng mức độ vận dụng, vận dụng cao có đáp án và lời giải chi tiết
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
 |
 |
 |
 |
 |
 |
 |
 |









