20 bài tập vận dụng Ôn tập chương 2: Hàm số và đồ thị
Làm đề thiCâu hỏi 1 :
Cho đại lượng y tỉ lệ thuận với đại lượng x. Biết khi giá trị của x là -2 thì giá trị tương ứng của y là 3. Vậy hệ số tỉ lệ của y đối với x là:
- A 6
- B -6
- C \(\frac{-2}{3}\)
- D \(\frac{-3}{2}\)
Đáp án: D
Phương pháp giải:
Áp dụng định nghĩa của hai đại lượng tỉ lệ thuận.
Lời giải chi tiết:
Do x và y là hai đại lượng tỉ lệ thuận nên ta có: \(y=kx\Leftrightarrow k=\frac{y}{x}=\frac{3}{-2}=-\frac{3}{2}\)
Chọn D.
Câu hỏi 2 :
Giả sử M, N là hai điểm thuộc đồ thị hàm số y = 5x + 2
a) Tung độ của M bằng nhiêu, nếu hoành độ của M bằng 1
b) Hoành độ của N bằng bao nhiêu, nếu tung độ của N bằng 1?
- A a) \(M(1; -7).\)
b) \(N\left( \frac{1}{5};1 \right)\).
- B a) \(M(1; 7).\)
b) \(N\left( \frac{1}{5};1 \right)\).
- C a) \(M(1; -7).\)
b) \(N\left( \frac{-1}{5};1 \right)\).
- D a) \(M(1; 7).\)
b) \(N\left( \frac{-1}{5};1 \right)\).
Đáp án: D
Phương pháp giải:
Thay các tọa độ có sẵn vào hàm số để tìm các tọa độ còn lại, từ đó suy ra điểm cần tìm.
Lời giải chi tiết:
a) Do M có hoành độ bằng 1, nên \(x = 1.\)
Thay \(x = 1\) vào \(y = 5x + 2\) ta được: \(y = 5.1 + 2 = 7.\)
Do đó: \(M(1; 7).\)
b) Do điểm N có tung độ bằng 1, nên y = 1.
Thay y = 1 vào y = 5x + 2 ta được: \(1=5x+2\Leftrightarrow 5x=-1\Leftrightarrow x=\frac{-1}{5}\).
Do đó: \(N\left( \frac{-1}{5};1 \right)\).
Chọn D.
Câu hỏi 3 :
Ba đội máy cày cày ba thửa ruộng như nhau. Đội thứ nhất hoàn thành công việc trong 2 ngày. Đội thứ hai trong 3 ngày và đội thứ ba trong 4 ngày. Hỏi mỗi đội có mấy máy, biết rằng đội thứ nhất có nhiều hơn đội thứ ba 3 máy và năng suất như nhau.
Số máy của đội thứ nhất, thứ hai và thứ ba lần lượt là:
- A 8 máy; 4 máy và 3 máy.
- B 8 máy; 4 máy và 2 máy.
- C 6 máy; 4 máy và 3 máy.
- D 6 máy; 4 máy và 2 máy.
Đáp án: C
Phương pháp giải:
Áp dụng tính chất của tỉ lệ nghịch, tính chất của dãy tỉ số bằng nhau để giải bài toán.
Lời giải chi tiết:
Gọi số máy cày của đội thứ nhất, đội thứ hai và đội thứ ba lần lượt là x, y, z(\(x,\,y,\,z\,\,\in \,\,{{N}^{*}}\)).
Cùng cày thửa ruộng như nhau và năng suất các máy như nhau thì số máy cày và thời gian cày là hai đại lượng tỉ lệ nghịch. Do đó x, y, z tỉ lệ nghịch với 2, 3, 4 và x – z = 3.
Ta có: \(2x=3y=4z\Rightarrow \frac{x}{6}=\frac{y}{4}=\frac{z}{3}=\frac{x-z}{6-3}=\frac{3}{3}=1\)
Do đó:
\(\begin{align} & \frac{x}{6}=1\Rightarrow x=6 \\ & \frac{y}{4}=1\Rightarrow y=4 \\ & \frac{z}{3}=1\Rightarrow z=3 \\ \end{align}\)
Vậy số máy cày của đội thứ nhât, đội thứ hai và đội thứ ba thứ tự là 6, 4, 3 máy.
Chọn C.
Câu hỏi 4 :
Cho hàm số y = ax.
a) Tìm a biết rằng điểm M(-3; 1) thuộc đồ thị hàm số.
b) Điểm N(-5;2) có thuộc đồ thị hàm số đó không?
Phương pháp giải:
Thay các điều kiện đã cho vào hàm số dã cho để tìm ra điều kiện còn lại.
Lời giải chi tiết:
a. Do M(-3; 1) thuộc đồ thị hàm số y = ax nên :
\(1=-3.a\Leftrightarrow a=-\frac{1}{3}\Rightarrow y=-\frac{1}{3}x\)
b. Thay tọa độ của điểm N vào hàm số ta được: Với \(x=-5\Rightarrow y=-\frac{1}{3}.\left( -5 \right)=\frac{5}{3}\ne 2.\)
\(\Rightarrow \) Điểm N không thuộc đồ thị hàm số \(y=-\frac{1}{3}x.\)
Câu hỏi 5 :
Ba lớp 7A1 , 7A2 , 7A3 hưởng ứng phong trào kế hoạch nhỏ đã thu được tổng cộng 370kg giấy vụn. Hãy tính số giấy vụn của mỗi lớp, biết rằng số giấy vụn thu được của ba lớp lần lượt tỉ lệ nghịch với 4; 6; 5.
- A 150(kg), 100(kg), 110(kg).
- B 150(kg), 120(kg), 120(kg).
- C 100(kg), 100(kg), 120(kg).
- D 150(kg), 100(kg), 120(kg).
Đáp án: D
Phương pháp giải:
Áp dụng tính chất của tỉ lệ nghịch, tính chất của dãy tỉ số bằng nhau để giải bài toán.
Lời giải chi tiết:
Gọi số giấy vụn thu được của các chi đội \(7A_{1};\,\,7{{A}_{2}};\,\,7{{A}_{3}}\) lần lượt là \(x;\,\,y;\,\,z\,\,\,\left( kg \right),\,\,\,\left( x,\,\,y,\,\,z>0 \right).\)
Theo bài ra, ta có: \(\frac{x}{\frac{1}{4}}=\frac{y}{\frac{1}{6}}=\frac{z}{\frac{1}{5}}\) và x + y + z = 370.
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\begin{array}{l}
\frac{x}{{\frac{1}{4}}} = \frac{y}{{\frac{1}{6}}} = \frac{z}{{\frac{1}{5}}} = \frac{{x + y + z}}{{\frac{1}{4} + \frac{1}{6} + \frac{1}{5}}} = \frac{{370}}{{\frac{{15 + 10 + 12}}{{60}}}} = \frac{{370}}{{\frac{{37}}{{60}}}} = 600\\
\Rightarrow \left\{ \begin{array}{l}
x = 600.\frac{1}{4} = 150\,\,kg\\
y = 600.\frac{1}{6} = 100\,\,kg\\
z = 600.\frac{1}{5} = 120\,\,kg
\end{array} \right..
\end{array}\)
Vậy Số giấy vụn thu được của các chi đội 7A1 , 7A2 , 7A3 lần lượt là : 150(kg), 100(kg), 120(kg).
Chọn D
Câu hỏi 6 :
Biết rằng y tỉ lệ nghịch với x theo hệ số tỉ lệ là 2 và z tỉ lệ nghịch với y theo hệ số tỉ lệ là 3. Hỏi z và x tỉ lệ thuận hay tỉ lệ nghịch và hệ số tỉ lệ là bao nhiêu?
Phương pháp giải:
Áp dụng khái niệm, tính chất của hai đại lượng tỉ lệ thuận, tỉ lệ nghịch.
Lời giải chi tiết:
Ta có : y tỉ lệ nghịch với x theo hệ số tỉ lệ là 2 nên \(y=\frac{2}{x}\)
z tỉ lệ nghịch với y theo hệ số tỉ lệ là 3 nên \(z=\frac{3}{y}\)
Do đó : \(z=\frac{3}{y}=3:\frac{2}{x}=\frac{3x}{2}.\)
Vậy z và x tỉ lệ thuận với nhau và hệ số tỉ lệ là \(\frac{3}{2}.\)
Câu hỏi 7 :
1) Tìm x biết: a) \(\left| \frac{1}{2}x-\frac{1}{6} \right|=\frac{1}{3}\) b) \({{\left( 4{{\text{x}}^{2}}-3 \right)}^{3}}+8=0\)
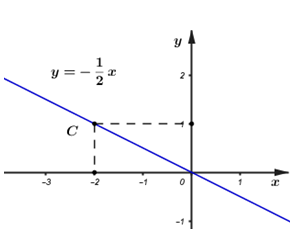
2) Vẽ đồ thị hàm số \(y=\frac{-1}{2}x\) Từ đó chứng minh 3 điểm A(2; -1), B(-12; -6) và C(-2; 1) không thẳng hàng.
- A a) \(x = 1\) hoặc \(x=-\frac{2}{3}.\)
b) \(x=\frac{-1}{2}\) hoặc \(x=\frac{1}{2}\)
- B a) \(x = 4\) hoặc \(x=-\frac{1}{3}.\)
b) \(x=\frac{5}{2}\) hoặc \(x=\frac{1}{2}\)
- C a) \(x = 1\) hoặc \(x=-\frac{1}{3}.\)
b) \(x=\frac{-1}{2}\) hoặc \(x=\frac{1}{2}\)
- D a) \(x = 0\) hoặc \(x=-\frac{2}{3}.\)
b) \(x=\frac{-1}{4}\) hoặc \(x=\frac{3}{2}\)
Đáp án: C
Phương pháp giải:
1) a) Áp dụng định nghĩa giá trị tuyệt đối của một số hữu tỉ để tìm x. \(\left| x \right|=\left\{ \begin{align} & x\ \ khi\ \ \ x\ge 0 \\ & -x\ \ \ khi\ \ x<0 \\ \end{align} \right..\)
b) Áp dụng công thức \({{A}^{3}}={{B}^{3}}\) thì \(A=B\) và \({{A}^{2}}={{B}^{2}}\) thì \(\left[ \begin{align} & A=B \\ & A=-B \\ \end{align} \right.\) để tìm x.
2) Tìm một điểm thuộc hàm số đã cho. Đồ thị của hàm số đã cho là đường thẳng đi qua gốc tọa độ và điểm thuộc hàm số đã cho đã tìm được.
Để chứng minh 3 điểm không thẳng hàng ta chứng minh có ít nhất một điểm không thuộc cùng 1 đường thẳng, hay không cùng thuộc đồ thị của hàm số đã cho.
Lời giải chi tiết:
1) a) \(\left| \frac{1}{2}x-\frac{1}{6} \right|=\frac{1}{3}\)
- Nếu \(\frac{1}{2}x-\frac{1}{6}\ge 0\) tức \(x\ge \frac{1}{3}\) thì \(\left| \frac{1}{2}x-\frac{1}{6} \right|=\frac{1}{2}x-\frac{1}{6}\)
Ta có phương trình \(\Leftrightarrow \frac{1}{2}x-\frac{1}{6}=\frac{1}{3}\Leftrightarrow \frac{1}{2}x=\frac{1}{3}+\frac{1}{6}\Leftrightarrow \frac{1}{2}x=\frac{1}{2}\Leftrightarrow x=1\ \ \ \ \left( tmdk\ \ x\ge \frac{1}{3} \right)\)
- Nếu \(\frac{1}{2}x-\frac{1}{6}<0\) tức là x < \(\frac{1}{3}\) thì \(\left| \frac{1}{2}x-\frac{1}{6} \right|=-\left( \frac{1}{2}x-\frac{1}{6} \right)=\frac{1}{6}-\frac{1}{2}x\)
Ta có phương trình \(\Leftrightarrow \frac{1}{6}-\frac{1}{2}x=\frac{1}{3}\Leftrightarrow \frac{1}{2}x=\frac{1}{6}-\frac{1}{3}\Leftrightarrow \frac{1}{2}x=\frac{-1}{6}\Leftrightarrow x=\frac{-1}{3}\ \ \ \left( tmdk\ \ x<\frac{1}{3} \right)\)
Vậy \(x = 1\) hoặc \(x=-\frac{1}{3}.\)
b)
\(\begin{array}{l}
\;\;\;\;{\left( {4{x^2} - 3} \right)^3} + 8 = 0 \Leftrightarrow {\left( {4{x^2} - 3} \right)^3} = - 8\\
\Leftrightarrow 4{x^2} - 3 = - 2 \Leftrightarrow 4{x^2} = 1\\
\Leftrightarrow {x^2} = \frac{1}{4} \Leftrightarrow \left| x \right| = \frac{1}{2} \Leftrightarrow \left[ \begin{array}{l}
x = \frac{1}{2}\\
x = - \frac{1}{2}
\end{array} \right..
\end{array}\)
Vậy \(x=\frac{-1}{2}\) hoặc \(x=\frac{1}{2}\)
2) Vẽ đồ thị hàm số \(y=-\frac{1}{2}x\) .
- Khi \(x=-2\) thì \(y=\frac{-1}{2}.\left( -2 \right)=1\)
Vậy điểm \(C\left( -2;\ 1 \right)\) thuộc đồ thị của hàm số . \(y=-\frac{1}{2}x\)
Đồ thị của hàm số này là đường thẳng OC trong hình vẽ bên.
- Xét điểm A, B thấy điểm C thuộc đồ thị \(y=-\frac{1}{2}x\) còn điểm B không thuộc đồ thị , thật vậy:
+ Khi x = \(-12\) thì \(y=\frac{-1}{2}.(-12)=6\ne -6\) nên điểm B(\(-12;\ -6\)) không thuộc đồ thị \(y=-\frac{1}{2}x\).
+ Khi \(x=2\) thì \(y=\frac{-1}{2}.2=-1\) nên điểm \(A\left( 2;-1 \right)\) thuộc đồ thị \(y=-\frac{1}{2}x\)
Điểm A, C thuộc đồ thị \(y=-\frac{1}{2}x\) còn điểm B không thuộc đồ thị \(y=-\frac{1}{2}x\) nên 3 điểm A, B, C không thẳng hàng. (đpcm)
Chọn C
Câu hỏi 8 :
a) Cho hàm số \(y = f(x) = 2{x^2} - 3\). Tính: \(f(0)\,;\,\,\,f(2)\).
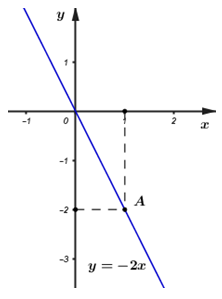
b) Vẽ đồ thị hàm số \(y = - 2x\).
- A \(a)\,\,f\left( 0 \right) = - 3\,;\,\,\,\,\,f\left( 2 \right) = - 5\)
- B \(a)\,\,f\left( 0 \right) = - 3\,;\,\,\,\,\,f\left( 2 \right) = 5\)
- C \(a)\,\,f\left( 0 \right) = 3\,;\,\,\,\,\,f\left( 2 \right) = 5\)
- D \(a)\,\,f\left( 0 \right) = 3\,;\,\,\,\,\,f\left( 2 \right) = - 5\)
Đáp án: B
Phương pháp giải:
a) Thay các giá trị \(x = 0;\,x = 2\) vào \(f(x)\) rồi tính giá trị.
b) Đồ thị hàm số \(y = - 2x\) là một đường thẳng đi qua gốc tọa độ \(O\). Do đó ta chỉ cần tìm thêm một điểm \(A\) nằm trên đường thẳng đó bằng cách thay \(x\) bằng một giá trị bất kì rồi tìm \(y\) tương ứng. Đồ thị hàm số \(y = - 2x\) chính là đường thẳng \(OA\).
Lời giải chi tiết:
a) Ta có:
\(\begin{array}{l}f(0) = {2.0^2} - 3 = 2.0 - 3 = 0 - 3 = - 3\\f(2) = {2.2^2} - 3 = 2.4 - 3 = 8 - 3 = 5\end{array}\)
b) Vẽ đồ thị hàm số \(y = - 2x\)
Đồ thị hàm số \(y = - 2x\) là một đường thẳng đi qua gốc tọa độ \(O\).
Cho \(x = 1\) suy ra \(y = - 2.1 = - 2\). Khi đó ta có điểm \(A(1; - 2)\).
Đồ thị hàm số \(y = - 2x\) là đường thẳng \(OA\) (xem hình vẽ)
Chọn B.
Câu hỏi 9 :
Cho hàm số \(y = f\left( x \right) = - \frac{2}{5}x + 3\). Tính: \(f\left( { - 5} \right)\,\,;\,\,f\left( {0,7} \right)\,\,;\,\,f\left( {3\frac{1}{4}} \right)\). Kết quả lần lượt là:
- A \(f\left( { - 5} \right) = 5\); \(f\left( {0,7} \right) = \frac{{38}}{{25}}\); \(f\left( {3\frac{1}{4}} \right) = f\left( {\frac{{13}}{4}} \right) = \frac{{17}}{{10}}\)
- B \(f\left( { - 5} \right) = 5\); \(f\left( {0,7} \right) = \frac{{-68}}{{25}}\); \(f\left( {3\frac{1}{4}} \right) = f\left( {\frac{{13}}{4}} \right) = \frac{{17}}{{10}}\)
- C \(f\left( { - 5} \right) = -5\); \(f\left( {0,7} \right) = \frac{{68}}{{25}}\); \(f\left( {3\frac{1}{4}} \right) = f\left( {\frac{{13}}{4}} \right) = \frac{{17}}{{10}}\)
- D \(f\left( { - 5} \right) = 5\); \(f\left( {0,7} \right) = \frac{{68}}{{25}}\); \(f\left( {3\frac{1}{4}} \right) = f\left( {\frac{{13}}{4}} \right) = \frac{{17}}{{10}}\)
Đáp án: D
Phương pháp giải:
Thay lần lượt \(x = - 5\) ; \(x = 0,7\) ; \(x = 3\frac{1}{4} = \frac{{13}}{4}\) vào hàm số để tính.
Lời giải chi tiết:
\(f\left( { - 5} \right) = \frac{{ - 2}}{5}.\left( { - 5} \right) + 3 = 2 + 3 = 5\)
\(f\left( {0,7} \right) = \frac{{ - 2}}{5}.0,7 + 3 = \frac{{ - 2}}{5}.\frac{7}{{10}} + 3 = \frac{{ - 7}}{{25}} + 3 = \frac{{68}}{{25}}\)
\(f\left( {3\frac{1}{4}} \right) = f\left( {\frac{{13}}{4}} \right) = \frac{{ - 2}}{5}.\frac{{13}}{4} + 3 = \frac{{ - 13}}{{10}} + 3 = \frac{{17}}{{10}}\)
Chọn đáp án D
Câu hỏi 10 :
Giải các bài toán sau:
Câu 1: \(\) Cho biết \(x\) và \(y\) là hai đại lượng tỉ lệ thuận, biết khi \(x = 3\) thì \(y = 15.\) Tìm hệ số tỉ lệ của \(y\) đối với \(x.\)
- A \(k=3\)
- B \(k=5\)
- C \(k=-3\)
- D \(k=1\)
Đáp án: B
Phương pháp giải:
Nếu đại lượng \(y\) tỉ lệ thuận với đại lượng \(x\) theo công thức: \(y = kx\) (với \(k\) là hằng số khác 0) thì ta nói \(y\) thỉ lệ thuận với \(x\) theo hệ số tỉ lệ \(k.\)
Để tìm hệ số tỉ lệ, khi biết giá trị của \(x\) và giá trị của \(y\) ta có:
\( \Rightarrow k = \frac{y}{x}\) . Thay các giá trị của \(y\) và \(x\) đề bài cho, ta tìm được \(k.\)
Lời giải chi tiết:
\(y\) tỉ lệ thuận với \(x\) theo hệ số tỉ lệ \(k\) \( \Rightarrow y = kx \Rightarrow k = \frac{y}{x} = \frac{{15}}{3} = 5\).
Chọn B
Câu 2: \(\) Vẽ đồ thị hàm số \(y = 2x.\) Đồ thị hàm số không đi qua điểm nào trong các điểm sau:
- A Gốc tọa độ O.
- B M(-1;-2)
- C N(2;4)
- D Q(-1;3)
Đáp án: D
Phương pháp giải:
Lấy đúng giá trị.
Vẽ đúng hệ trục tọa độ và đồ thị hàm số.
Lời giải chi tiết:
Vẽ đồ thị hàm số \(y = 2x\) . Ta có bảng:

Đồ thị hàm số là đường thẳng đi qua gốc tọa độ \(O\left( {0;0} \right)\) và các điểm:
\(A\left( { - 2; - 4} \right);\,B\left( { - 1; - 2} \right);\,C\left( {1;2} \right);\,D\left( {2;4} \right)\).
Đồ thị hàm số đối xứng qua gốc tọa độ O.
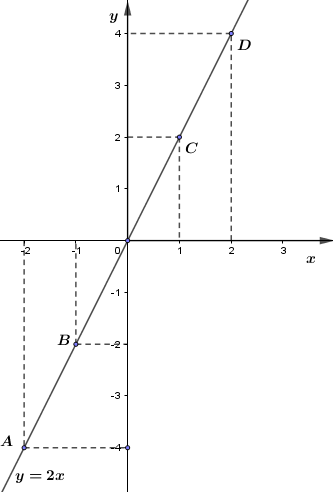
Chọn D
Câu 3: \(\,\) Hỏi điểm \(A\left( { - 2;4} \right)\) có thuộc đồ thị hàm số \(y = 2x\) không? Vì sao?
- A Không xác định được.
- B \(A\left( { - 2;4} \right)\) thuộc đồ thị hàm số \(y = 2x\).
- C \(A\left( { - 2;4} \right)\) không thuộc đồ thị hàm số \(y = 2x\).
- D \(A\left( { - 2;4} \right)\) vừa thuộc đồ thị hàm số \(y = 2x\), vừa không thuộc đồ thị hàm số \(y = x\)
Đáp án: C
Phương pháp giải:
Thay \(x = - 2\) vào hàm số \(y = 2x\) ta có: \(y = 2.\left( { - 2} \right) = - 4 \ne 4\)
Vậy điểm \(A\left( { - 2;4} \right)\) không thuộc đồ thị hàm số \(y = 2x\)
Lời giải chi tiết:
Thay \(x = - 2\) vào hàm số \(y = 2x\) ta có: \(y = 2.\left( { - 2} \right) = - 4 \ne 4\).
Vậy điểm \(A\left( { - 2;4} \right)\) không thuộc đồ thị hàm số \(y = 2x\).
Chọn C
Câu 4: \(\,\) Biết điểm \(B\left( {3;m + 1} \right)\) thuộc đồ thị hàm số \(y = 2x\). Tìm \(m.\)
- A \(m=1\)
- B \(m=8\)
- C \(m=3\)
- D \(m=5\)
Đáp án: D
Phương pháp giải:
Điểm \(B\left( {3;\,m + 1} \right)\) thuộc đồ thị hàm số \(y = 2x\), do đó tọa độ của điểm B thỏa mãn \(y = 2x\).
Thay tọa độ của B vào \(y = 2x\) ta tìm được m.
Lời giải chi tiết:
Điểm \(B\left( {3;\,m + 1} \right)\) thuộc đồ thị hàm số \(y = 2x\) nên tọa độ của B thỏa mãn \(y = 2x\).
\( \Rightarrow m + 1 = 2.3 = 6 \Leftrightarrow m = 6 - 1 \Leftrightarrow m = 5.\) Vậy \(m = 5\) là giá trị cần tìm.
Chọn D
Câu hỏi 11 :
Giải các bài toán sau:
Câu 1: Viết các phân số sau dưới dạng số thập phân hữu hạn, số thập phân vô hạn tuần hoàn (dạng thu gọn): \(\frac{{24}}{{32}};\,\frac{8}{{15}}\).
- A \(\begin{array}{l}\frac{{24}}{{32}} = \frac{{24:8}}{{32:8}} = \frac{3}{4} = 0,75\\\frac{8}{{15}} = 0,533333... = 0,5\left( 3 \right)\end{array}\)
- B \(\begin{array}{l}\frac{{24}}{{32}} = \frac{{24:8}}{{32:8}} = \frac{3}{4} = 0,75\\\frac{8}{{15}} = 0,5555555... = 0,5\left( 5 \right)\end{array}\)
- C \(\begin{array}{l}\frac{{24}}{{32}} = \frac{{24:8}}{{32:8}} = \frac{3}{4} = 0,75\\\frac{8}{{15}} = 0,6666666... = 0,6\left( 6 \right)\end{array}\)
- D \(\begin{array}{l}\frac{{24}}{{32}} = \frac{{24:8}}{{32:8}} = \frac{3}{4} = 0,75\\\frac{8}{{15}} = 0,3333333... = 0,3\left( 3\right)\end{array}\)
Đáp án: A
Phương pháp giải:
Nhớ lại: Viết phân số dưới dạng số thập phân hữu hạn hoặc số thập phân vô hạn tuần hoàn:
- Nếu một phân số tối giản mà mẫu không có ước nguyên tố khác 2 và 5 thì viết được dưới dạng số thập phân hữu hạn (STPHH).
- Nếu một phân số tối giản mà mẫu có ước nguyên tố khác 2 và 5 thì không viết được dưới dạng số thập phân hữu hạn. Phân số đó viết thành số thập phân vô hạn, trong đó có những nhóm chữ số được lặp lại, nhóm chữ số đó gọi là chu kỳ, số thập phân vô hạn đó gọi là số thập phân vô hạn tuần hoàn (STPVHTH)
+ Số thập phân có nguồn gốc từ phân số nếu vô hạn thì phải tuần hoàn
+ Ví dụ: Khi chia 1 cho 7 ta được số thập phân vô hạn, số dư trong phép chia này chỉ có thể là 1, 2, 3, 4, 5, 6 nếu nhiều nhất đến số dư thứ 7, số dư phải lặp lại, do đó các nhóm chữ số cũng thường lặp lại, và số thập phân vô hạn phải tuần hoàn.
\( \Rightarrow \) Để viết phân số dưới dạng số thập phân hữu hạn hoặc số thập phân vô hạn tuần hoàn ta rút gọn phân số, rồi lấy tử số của phân số đã thu gọn chia cho mẫu số của nó.
Lời giải chi tiết:
Viết phân số dưới dạng số thập phân hữu hạn hoặc số thập phân vô hạn tuần hoàn (thu gọn):
\(\begin{array}{l}\frac{{24}}{{32}} = \frac{{24:8}}{{32:8}} = \frac{3}{4} = 0,75\\\frac{8}{{15}} = 0,533333... = 0,5\left( 3 \right)\end{array}\)
Chọn A
Câu 2: Cho hàm số: \(y = f\left( x \right) = {x^2} + 1\) . Tính \(f\left( 0 \right);\,f\left( { - 2} \right)\).
- A \(f\left( 0 \right) =- 1\) và \(f\left( { - 2} \right) = 5\).
- B \(f\left( 0 \right) = 1\) và \(f\left( { - 2} \right) = 5\).
- C \(f\left( 0 \right) = 1\) và \(f\left( { - 2} \right) = -5\).
- D \(f\left( 0 \right) = -1\) và \(f\left( { - 2} \right) = -5\).
Đáp án: B
Phương pháp giải:
Thay \(x = 0,\,\,x = - 2\) vào \(y = f\left( x \right) = {x^2} + 1\) để tìm \(f\left( 0 \right);\,f\left( { - 2} \right)\).
Lời giải chi tiết:
Thay \(x = 0\) vào \(y = f\left( x \right) = {x^2} + 1\) . Ta có \(f\left( 0 \right) = {0^2} + 1 = 1\).
Thay\(\,\,x = - 2\) vào \(y = f\left( x \right) = {x^2} + 1\). Ta có \(f\left( { - 2} \right) = {\left( { - 2} \right)^2} + 1 = 4 + 1 = 5\)
Vậy \(f\left( 0 \right) = 1\) và \(f\left( { - 2} \right) = 5\).
Chọn B
Câu 3: Cho hai đại lượng \(x\) và \(y\) tỉ lệ nghịch với nhau. Biết \(x = 5\) thì \(y = 2\). Tìm hệ số tỉ lệ và biểu diễn \(y\) theo \(x\,?\)
- A Vì \(y\) tỉ lệ nghịch với \(x\) theo hệ số tỉ lệ \(a = 5\). Khi đó \(y = \frac{a}{x} = \frac{{5}}{x}\).
- B Vì \(y\) tỉ lệ nghịch với \(x\) theo hệ số tỉ lệ \(a = 2\). Khi đó \(y = \frac{a}{x} = \frac{{2}}{x}\).
- C Vì \(y\) tỉ lệ nghịch với \(x\) theo hệ số tỉ lệ \(a = 10\). Khi đó \(y = \frac{a}{x} = \frac{{10}}{x}\).
- D Vì \(y\) tỉ lệ nghịch với \(x\) theo hệ số tỉ lệ \(a = -10\). Khi đó \(y = \frac{a}{x} = \frac{{-10}}{x}\).
Đáp án: C
Phương pháp giải:
Nếu đại lượng \(y\) liên hệ với đại lượng \(x\) theo công thức \(y = \frac{a}{x}\,\,hay\,\,xy = a\) (\(a\) là hằng số khác 0)
thì ta nói \(y\) tỉ lệ nghịch với \(x\) theo hệ số tỉ lệ \(a\).
Ta có: \(y = \frac{a}{x} \Rightarrow x = \frac{a}{y} \Rightarrow a = xy\)
Lời giải chi tiết:
Nếu đại lượng \(y\) liên hệ với đại lượng \(x\) theo công thức \(y = \frac{a}{x}\,\,hay\,\,xy = a\) (\(a\) là hằng số khác 0)
thì ta nói \(y\) tỉ lệ nghịch với \(x\) theo hệ số tỉ lệ \(a\).
Ta có: \(y = \frac{a}{x} \Rightarrow x = \frac{a}{y} \Rightarrow a = xy\)
Biết \(x = 5\) thì \(y = 2 \Rightarrow a = x.y = 5.2 = 10\).
Vì \(y\) tỉ lệ nghịch với \(x\) theo hệ số tỉ lệ \(a = 10\). Khi đó \(y = \frac{a}{x} = \frac{{10}}{x}\).
Chọn C
Câu hỏi 12 :
Giải các bài toán sau:
Câu 1: Cho biết hai đại lượng \(x\) và \(y\) tỉ lệ thuận với nhau, khi \(x = 4\) thì \(y = 12\). Tìm hệ số tỉ lệ \(k\) của \(y\) đối với \(x\) và biểu diễn \(y\) theo \(x\).
- A \(k=2\)
- B \(k=3\)
- C \(k=4\)
- D \(k=-2\)
Đáp án: B
Phương pháp giải:
Nếu đại lượng \(y\) liên hệ với đại lượng \(x\) theo công thức \(y = \,kx\) (\(k\) là một hằng số khác 0) thì ta nói \(y\) tỉ lệ thuận với \(x\) theo hệ số tỉ lệ \(k.\)
Lời giải chi tiết:
Vì \(x\) và \(y\) tỉ lệ thuận với nhau, khi \(x = 4\) thì \(y = 12\) nên \( \Rightarrow k = \frac{y}{x} = \frac{{12}}{4} = 3\)
Vậy hệ số tỉ lệ \(k = 3\) .
Chọn B
Câu 2: Cho hàm số \(y = f\left( x \right) = 2{x^2} - 5\) . Tính \(f\left( {\frac{1}{2}} \right);\,f\left( { - 1} \right);\,f\left( 3 \right)\) .
\(f\left( {\frac{1}{2}} \right);\,f\left( { - 1} \right);\,f\left( 3 \right)\) . Lần lượt là:
- A \(10; -3; 13\)
- B \(\frac{{ - 9}}{{10}}; -3; 13\)
- C \(\frac{{ - 1}}{{3}}; -3; 13\)
- D \(3; -3; 13\)
Đáp án: B
Phương pháp giải:
+ Thay \(x = \frac{1}{2}\) vào \(y = f\left( x \right) = 2{x^2} - 5\) để tìm \(f\left( {\frac{1}{2}} \right)\)
+ Thay \(x = - 1\) vào \(y = f\left( x \right) = 2{x^2} - 5\) để tìm \(f\left( { - 1} \right)\)
+ Thay \(x = 3\) vào \(y = f\left( x \right) = 2{x^2} - 5\) để tìm \(f\left( 3 \right)\)
Lời giải chi tiết:
Cho hàm số \(y = f\left( x \right) = 2{x^2} - 5\) . Tính \(f\left( {\frac{1}{2}} \right);\,f\left( { - 1} \right);\,f\left( 3 \right)\).
+ Thay \(x = \frac{1}{2}\) vào \(y = f\left( x \right) = 2{x^2} - 5\) . Ta có: \(f\left( {\frac{1}{2}} \right) = 2.{\left( {\frac{1}{2}} \right)^2} - 5 = \frac{1}{2} - 5 = \frac{{ - 9}}{{10}}\)
+ Thay \(x = - 1\) vào \(y = f\left( x \right) = 2{x^2} - 5\) . Ta có: \(f\left( { - 1} \right) = 2.{\left( { - 1} \right)^2} - 5 = 2 - 5 = - 3\)
+ Thay \(x = 3\) vào \(y = f\left( x \right) = 2{x^2} - 5\) . Ta có: \(f\left( 3 \right) = {2.3^2} - 5 = 2.9 - 5 = 13\)
Chọn B
Câu hỏi 13 :
Giải các bài toán sau:
Câu 1: Tìm \(x\) biết: \(\,5 + \frac{2}{3}:x = 7\)
- A \(x=2\)
- B \(x=3\)
- C \(x=\frac{-1}{3}\)
- D \(x=\frac{1}{3}\)
Đáp án: D
Phương pháp giải:
Tìm \(\frac{2}{3}:x\) bằng cách chuyển \(5\) ở vế phải sang vế trái, đổi dấu thành \( - 5\). Sau đó thực hiện phép tính bên vế phải. Sau khi thực hiện phép tính bên vế phải xong, ta lấy \(\frac{2}{3}\) chia cho kết quả vừa tìm được thì tìm ra \(x.\)
Lời giải chi tiết:
\(\begin{array}{l}\,\,\,5 + \frac{2}{3}:x = 7\\\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{2}{3}:x\, = 7 - 5\\\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{2}{3}:x = 2\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = \frac{2}{3}:2\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = \frac{1}{3}\end{array}\)
Chọn D
Câu 2: Tìm \(x\) biết: \(\,\left| {x - \frac{1}{3}} \right| - 0,25 = \frac{3}{4}\)
- A \(x = \frac{4}{3}\)
- B \(x = \frac{{ - 2}}{3}\)
- C \(x = \frac{4}{3}\) hoặc \(x = \frac{{ - 2}}{3}\)
- D \(x = \frac{4}{3}\) hoặc \(x = \frac{{ 2}}{3}\)
Đáp án: C
Phương pháp giải:
Viết \(0,25\) về dạng phân số ta được \(0,25 = \frac{1}{4}\) , chuyển \(\frac{{ - 1}}{4}\) từ vế trái sang vế phải ta đổi dấu thành \( + \frac{1}{4}\) , sau đó thực hiện phép tính bên vế phải ta được \(\left| {x - \frac{1}{3}} \right| = 1\) , rồi xét 2 trường hợp: TH1: \(x - \frac{1}{3} \ge 0\) , TH2: \(x - \frac{1}{3} < 0\)
Lời giải chi tiết:
\(\begin{array}{l}\,\,\,\,\left| {x - \frac{1}{3}} \right| - 0,25 = \frac{3}{4}\\\,\,\,\,\,\left| {x - \frac{1}{3}} \right|\, - \frac{1}{4}\,\,\,\,\,\,\,\, = \frac{3}{4}\\\,\,\,\,\,\left| {x - \frac{1}{3}} \right|\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 1\end{array}\)
TH1: \(x - \frac{1}{3} \ge 0 \Leftrightarrow x \ge \frac{1}{3}\)
Ta có: \(\left| {x - \frac{1}{3}} \right| = 1 \Leftrightarrow x - \frac{1}{3} = 1 \Leftrightarrow x = \frac{1}{3} + 1 = \frac{4}{3}\,\,\,\left( {TM} \right)\)
TH2: \(x - \frac{1}{3} < 0 \Leftrightarrow x < \frac{1}{3}\)
Ta có: \(\left| {x - \frac{1}{3}} \right| = - 1 \Leftrightarrow x - \frac{1}{3} = - 1 \Leftrightarrow x = \frac{1}{3} - 1 = \frac{{ - 2}}{3}\,\,\left( {TM} \right)\)
Vậy \(x = \frac{4}{3}\) hoặc \(x = \frac{{ - 2}}{3}\)
Chọn C
Câu 3: Tìm \(x,y\) biết: \(\,7x = 2y\) và \(3x - y = - 9\)
- A \(x = 14;\,y = 63\).
- B \(x = 18;\,y = 63\).
- C \(x = -18;\,y = 63\).
- D \(x = -18;\,y = -63\).
Đáp án: B
Phương pháp giải:
Rút \(y\) từ \(3x - y = - 9\) ta được \(y = 3x + 9\) , sau đó thay vào \(7x = 2y\), ta tìm được \(x\) rồi thay ngược lại vào \(y = 3x + 9\)ta tìm được \(y\), rồi đưa ra kết luận.
Lời giải chi tiết:
\(\,7x = 2y\) và \(3x - y = - 9\)
Ta có: \(3x - y = - 9 \Rightarrow y = 3x + 9\) thay vào \(7x = 2y\) ta được:
\(\begin{array}{l}7x = 2.\left( {3x + 9} \right)\\ \Leftrightarrow 7x = 6x + 18\\ \Leftrightarrow 7x - 6x = 18\\ \Leftrightarrow \,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,\, = 18\end{array}\)
\(\begin{array}{l} \Rightarrow y = 3.18 + 9\\ \Rightarrow y = 63\end{array}\)
Vậy \(x = 18;\,y = 63\).
Chọn B
Câu 4: Ba lớp 7A, 7B, 7C đi lao động trồng cây xanh. Biết rằng số cây trồng được của mỗi lớp tỷ lệ với các số 4; 3; 6 và số cây trồng được của lớp 7B ít hơn lớp 7C là 21 cây. Hỏi mỗi lớp trồng được bao nhiêu cây?
Số cây ba lớp 7A, 7B, 7C trồng được lần lượt là:
- A \(29;21;41\)
- B \(31;20;40\)
- C \(28;21;42\)
- D \(23;21;42\)
Đáp án: C
Phương pháp giải:
Gọi \(x;y;z\) lần lượt là số cây mà các lớp 7A, 7B, 7C trồng được. Sau đó, áp dụng tính chất dãy tỉ số bằng nhau để tìm ra \(x;y;z\).
Lời giải chi tiết:
Gọi số cây của ba lớp 7A, 7B, 7C lần lượt là \(x;y;z\,\,\left( {x,y,z \in N*} \right)\)
Theo đề bài ta có: \(\frac{x}{4} = \frac{y}{3} = \frac{z}{6}\) và \(z - y = 21\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\begin{array}{l}\frac{x}{4} = \frac{y}{3} = \frac{z}{6} = \frac{{z - y}}{{6 - 3}} = \frac{{21}}{3} = 7\\ \Rightarrow \left\{ \begin{array}{l}x = 7.4 = 28\\y = 7.3 = 21\\z = 7.6 = 42\end{array} \right.\,\,\,(TM)\end{array}\)
Vậy lớp 7A trồng được 28 cây, lớp 7B trồng được 21 cây, lớp 7C trồng được 42 cây.
Chọn C
Câu hỏi 14 :
Cho hàm số \(y = f\left( x \right) = - 4x + 1\)
Câu 1: Tính \(f\left( { - 1} \right);\,f\left( {\frac{1}{2}} \right)?\)
- A \(f\left( { - 1} \right) = -5;\,\,f\left( {\frac{1}{2}} \right) = - 2\).
- B \(f\left( { - 1} \right) = 5;\,\,f\left( {\frac{1}{2}} \right) = - 3\).
- C \(f\left( { -1} \right) = 5;\,\,f\left( {\frac{1}{2}} \right) = 4\).
- D \(f\left( { - 1} \right) = 5;\,\,f\left( {\frac{1}{2}} \right) = - 1\).
Đáp án: D
Phương pháp giải:
Thay \(x = - 1\) vào \(y = f\left( x \right) = - 4x + 1\) để tìm \(f\left( { - 1} \right)\) . Thay \(x = \frac{1}{2}\) vào \(y = f\left( x \right) = - 4x + 1\) để tìm \(f\left( {\frac{1}{2}} \right)\).
Lời giải chi tiết:
Thay \(x = - 1\) vào \(y = f\left( x \right) = - 4x + 1\) ta có: \(f\left( { - 1} \right) = - 4.\left( { - 1} \right) + 1 = 4 + 1 = 5\)
Thay \(x = \frac{1}{2}\) vào \(y = f\left( x \right) = - 4x + 1\) ta có: \(f\left( {\frac{1}{2}} \right) = - 4.\frac{1}{2} + 1 = - 1\)
Vậy \(f\left( { - 1} \right) = 5;\,\,f\left( {\frac{1}{2}} \right) = - 1\).
Chọn D
Câu 2: Tìm giá trị của \(x\) để \(y = 0;\,y = - 3\).
- A \(y = 0\) thì \(x = \frac{1}{4}\) \(y = 3\) thì \(x = 1\).
- B \(y = 0\) thì \(x = \frac{1}{4}\) \(y = - 3\) thì \(x = 1\).
- C \(y = 0\) thì \(x = \frac{-1}{4}\) \(y = - 3\) thì \(x = 1\).
- D \(y = 0\) thì \(x = \frac{1}{4}\) \(y = - 3\) thì \(x =- 1\).
Đáp án: B
Phương pháp giải:
Thay \(y = 0\) vào \(y = f\left( x \right) = - 4x + 1\)để tìm x. Thay \(y = - 3\) vào \(y = f\left( x \right) = - 4x + 1\)để tìm x.
Lời giải chi tiết:
Khi \(y = 0\) . Ta có: \( - 4x + 1 = 0 \Leftrightarrow - 4x = - 1 \Leftrightarrow x = \frac{1}{4}\).
Khi \(y = - 3\) . Ta có: \( - 4x + 1 = - 3 \Leftrightarrow - 4x = - 4 \Leftrightarrow x = 1\).
Chọn B
Câu hỏi 15 :
Cho hàm số \(y = f\left( x \right) = 3x - 1\).
Câu 1:
Tính \(f\left( {\frac{{ - 1}}{3}} \right)\,;\,\,\,\,f\left( 0 \right)\).
- A \(f\left( {\frac{{ - 1}}{3}} \right) = - 2\,;\,\,\,\,f\left( 0 \right) = - 1.\)
- B \(f\left( {\frac{{ - 1}}{3}} \right) = - 1\,;\,\,\,\,f\left( 0 \right) = - 2.\)
- C \(f\left( {\frac{{ - 1}}{3}} \right) = 2\,;\,\,\,\,f\left( 0 \right) = - 1.\)
- D \(f\left( {\frac{{ - 1}}{3}} \right) = 2\,;\,\,\,\,f\left( 0 \right) = 1.\)
Đáp án: A
Phương pháp giải:
Thay các giá trị \(x = \frac{{ - 1}}{3};\,x = 0\) vào \(f(x)\) rồi tính giá trị tương ứng của \(y\).
Lời giải chi tiết:
Cho hàm số \(y = f\left( x \right) = 3x - 1\).
Tính \(f\left( {\frac{{ - 1}}{3}} \right)\,;\,\,\,\,f\left( 0 \right)\).
Với \(x = \frac{{ - 1}}{3}\) ta có \(y = f\left( {\frac{{ - 1}}{3}} \right) = 3.\frac{{ - 1}}{3} - 1 = - 1 - 1 = - 2\).
Với \(x = 0\) ta có \(y = f\left( 0 \right) = 3.0 - 1 = - 1\)
Vậy \(f\left( {\frac{{ - 1}}{3}} \right) = - 2\,;\,\,\,\,f\left( 0 \right) = - 1.\)
Chọn A
Câu 2:
Tìm \(x\) khi \(y = - 1\).
- A \(x = 0\).
- B \(x = 1\).
- C \(x = -2\).
- D \(x = -1\).
Đáp án: A
Phương pháp giải:
Thay giá trị của \(y\) vào biểu thức rồi tìm giá trị tương ứng của \(x\).
Lời giải chi tiết:
Tìm \(x\) khi \(y = - 1\).
Với \(y = - 1\) ta có: \( - 1 = 3x - 1 \Rightarrow 3x = 0 \Rightarrow x = 0\)
Vậy khi \(y = - 1\) thì \(x = 0\).
Chọn A
Câu hỏi 16 :
Cho hàm số \(y = f\left( x \right) = 2x + 1\)
Câu 1:
Tính \(f\left( {\frac{1}{2}} \right)\).
- A \(f\left( {\frac{1}{2}} \right) = 1\).
- B \(f\left( {\frac{1}{2}} \right) = -2\).
- C \(f\left( {\frac{1}{2}} \right) = 2\).
- D \(f\left( {\frac{1}{2}} \right) = -1\).
Đáp án: C
Phương pháp giải:
Thay giá trị \(x = \frac{1}{2}\) vào \(f\left( x \right)\) rồi tính giá trị tương ứng của \(y.\)
Lời giải chi tiết:
Tính \(f\left( {\frac{1}{2}} \right)\).
Thay \(x = \frac{1}{2}\) vào hàm số \(y = f\left( x \right) = 2x + 1\) ta được:
\(f\left( {\frac{1}{2}} \right) = 2.\frac{1}{2} + 1 = 1 + 1 = 2\).
Chọn C
Câu 2:
Tính giá trị của \(x\) tại \(y = - 1\).
- A \(x = - 2\).
- B \(x = - 1\).
- C \(x = - 3\).
- D \(x = - 5\).
Đáp án: B
Phương pháp giải:
Thay giá trị của \(y\) vào biểu thức rồi tìm giá trị tương ứng của \(x\).
Lời giải chi tiết:
Tính giá trị của \(x\) tại \(y = - 1\).
Với\(y = - 1\) ta có : \(2x + 1 = - 1 \Leftrightarrow 2x = - 2 \Leftrightarrow x = - 1\).
Chọn B
Câu hỏi 17 :
a) Vẽ đồ thị hàm số \(y = \frac{3}{2}x\).
b) Cho \(A\left( {12;18} \right)\) và \(B\left( {20;25} \right)\). Hỏi đồ thị của hàm số trên đi qua điểm nào trong hai điểm đã cho? Giải thích?
Phương pháp giải:
a) Lấy hai điểm thuộc đồ thị hàm số :
- Cho \(x = 0\) tìm giá trị của \(y.\)
- Cho \(x = 1\) tìm giá trị tương ứng của \(y.\)
Nối hai điểm vừa tìm được, ta có đồ thị của hàm số.
b) Vận dụng kiến thức : Điểm \(A\left( {{x_A},{y_A}} \right)\) thuộc đồ thị của hàm số \(y = ax\) khi \({y_A} = a{x_A}.\)
Lời giải chi tiết:
a) Vẽ đồ thị hàm số \(y = \frac{3}{2}x\)
Khi \(x = 0\) thì \(y = \frac{3}{2} \cdot 0 = 0\)
Khi \(x = 1\) thì \(y = \frac{3}{2} \cdot 1 = \frac{3}{2}\)
Vẽ đường thẳng đi qua hai điểm \(A\left( {0;0} \right);\,B\left( {1;\frac{3}{2}} \right)\), từ đó ta có đồ thị của hàm số \(y = \frac{3}{2}x\)
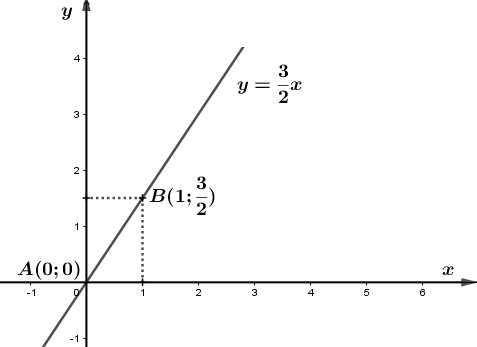
b) Cho \(A\left( {12;18} \right)\) và \(B\left( {20;25} \right)\). Hỏi đồ thị của hàm số trên đi qua điểm nào trong hai điểm đã cho? Giải thích?
Ta có :
\(18 = \frac{3}{2} \cdot 12\) nên điểm \(A\left( {12;18} \right)\) nằm trên đồ thị của hàm số \(y = \frac{3}{2}x\)
\(25 \ne \frac{3}{2} \cdot 20\) nên điểm \(B\left( {20;25} \right)\) không nằm trên đồ thị của hàm số \(y = \frac{3}{2}x\).
Câu hỏi 18 :
Trong mặt phẳng tọa độ vẽ tứ giác ABCD với A(-1; 1); B(2;-2);
C(1; 3); D(3; 0). Hãy chứng tỏ rằng ba điểm A, O, B thẳng hàng.
Phương pháp giải:
Để chứng minh ba điểm thẳng hàng ta chứng minh ba điểm cùng thuộc một đồ thị hàm số.
Lời giải chi tiết:
Ta thấy (-1) = (-1). 1; 2 = (-1).(-2); 0 = (-1).0.
Nên các điểm A(-1; 1); B(2; -2); và O(0; 0) cùng thuộc đồ thị hàm số y = -x.
Do đó ba điểm A, B, O thẳng hàng.
Câu hỏi 19 :
Giả sử \(\frac{x}{y}=4;\,\,\,xy=9.\) Ngoài ra \(x\ge 0.\) Khi đó \(\left( x;\,\,y \right)\) bằng?
- A \(\left( x;\,\,y \right)=\left( 3;\,\,\frac{3}{4} \right)\)
- B \(\left( x;\,\,y \right)=\left( 6;\,\,\frac{1}{2} \right)\)
- C \(\left( x;\,\,y \right)=\left( 6;\,\,\frac{3}{2} \right)\)
- D \(\left( x;\,\,y \right)=\left( 6;\,\,\frac{5}{2} \right)\)
Đáp án: C
Phương pháp giải:
Từ biểu thức thứ nhất ta suy ra được \(x=4y\) . Thay giá trị của \(x=4y\) vào biểu thức còn lại để tìm y. Từ đó suy ra \(x\) và nhớ chú ý điều kiện \(x\ge 0.\)
Lời giải chi tiết:
Ta có: \(\frac{x}{y}=4\Rightarrow x=4y.\)
Thay vào biểu thức \(xy=9\) ta được: \(4y.y=9\Leftrightarrow {{y}^{2}}=\frac{9}{4}\Leftrightarrow \left[ \begin{align} & y=\frac{3}{2} \\ & y=-\frac{3}{2} \\ \end{align} \right.\)
+) Với \(y=\frac{3}{2}\Rightarrow x=4.\frac{3}{2}=6\,\,\left( tm \right).\)
+) Với \(y=-\frac{3}{2}\Rightarrow y=4.\left( -\frac{3}{2} \right)=-6\,\,\,\left( ktm \right).\)
Vậy \(\left( x;\,\,y \right)=\left( 6;\,\,\frac{3}{2} \right)\)
Chọn C
Câu hỏi 20 :
Cho hàm số \(f\left( x \right)\) xác định với mọi \(x\) thuộc \(R\). Biết rằng với mọi \(x\) , ta đều có: \(f\left( x \right) + 2.f\left( {\frac{1}{x}} \right) = {x^2}.\) Tính \(f\left( {\frac{1}{3}} \right)\).
- A \(f\left( {\frac{1}{3}} \right) = \frac{{232}}{{27}}\).
- B \(f\left( {\frac{1}{3}} \right) = 27\).
- C \(f\left( {\frac{1}{3}} \right) = \frac{{169}}{{27}}\).
- D \(f\left( {\frac{1}{3}} \right) = \frac{{161}}{{27}}\).
Đáp án: D
Phương pháp giải:
+ Thay \(x = \frac{1}{3}\) vào \(f\left( x \right) + 2.f\left( {\frac{1}{x}} \right) = {x^2}\) ta được \(f\left( {\frac{1}{3}} \right) + 2.f\left( 3 \right) = \frac{1}{9}\).
+ Thay \(x = 3\) vào \(f\left( x \right) + 2.f\left( {\frac{1}{x}} \right) = {x^2}\) . Ta được:
\(\begin{array}{l}f\left( 3 \right) + 2.f\left( {\frac{1}{3}} \right) = 9\\ \Rightarrow f\left( 3 \right) = 9 - 2.f\left( {\frac{1}{3}} \right)\,\,\,\,\,\,\left( * \right)\end{array}\)
Thay \(\left( * \right)\) vào \(f\left( {\frac{1}{3}} \right) + 2.f\left( 3 \right) = \frac{1}{9}\) ta tìm được \(f\left( {\frac{1}{3}} \right)\).
Lời giải chi tiết:
+ Thay \(x = \frac{1}{3}\) vào \(f\left( x \right) + 2.f\left( {\frac{1}{x}} \right) = {x^2}\) ta được \(f\left( {\frac{1}{3}} \right) + 2.f\left( 3 \right) = \frac{1}{9}\).
+ Thay \(x = 3\) vào \(f\left( x \right) + 2.f\left( {\frac{1}{x}} \right) = {x^2}\) . Ta được: \(f\left( 3 \right) + 2.f\left( {\frac{1}{3}} \right) = 9 \Rightarrow f\left( 3 \right) = 9 - 2.f\left( {\frac{1}{3}} \right)\,\,\,\,\,\,\left( * \right)\)
+ Thay \(\left( * \right)\) vào \(f\left( {\frac{1}{3}} \right) + 2.f\left( 3 \right) = \frac{1}{9}\) .Ta được:
\(\begin{array}{l}f\left( {\frac{1}{3}} \right) + 2.f\left( 3 \right) = \frac{1}{9}\\ \Rightarrow f\left( {\frac{1}{3}} \right) + 2.\left[ {9 - 2.f\left( {\frac{1}{3}} \right)} \right] = \frac{1}{9}\\ \Rightarrow f\left( {\frac{1}{3}} \right) + 18 - 4.f\left( {\frac{1}{3}} \right) = \frac{1}{9}\\ \Rightarrow - 3.f\left( {\frac{1}{3}} \right) = \frac{1}{9} - 18\\ \Rightarrow 3.f\left( {\frac{1}{3}} \right) = 18 - \frac{1}{9}\\ \Rightarrow f\left( {\frac{1}{3}} \right) = 6 - \frac{1}{{27}} = \frac{{161}}{{27}}\end{array}\)
Vậy \(f\left( {\frac{1}{3}} \right) = \frac{{161}}{{27}}\).
Chọn D
>> Học trực tuyến lớp 7 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 7 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
 |
 |
 |
 |
 |
 |
Các bài khác cùng chuyên mục