15 bài tập vận dụng về Ứng dụng thực tế các tỉ số lượng giác của góc nhọn
Làm đề thiCâu hỏi 1 :
Một học sinh dùng kế giác, đứng cách chân cột cờ \(10m\) rồi chỉnh mặt thước ngắm cao bằng mắt của mình để xác định góc "nâng" (góc tạo bởi tia sáng đi thẳng từ đỉnh cột cờ với mắt tạo với phương nằm ngang). Khi đó, góc "nâng" đo được \({31^0}\). Biết khoảng cách từ mặt sân đến mắt học sinh đó bằng \(1,5m\). Tính chiều cao cột cờ (kết quả làm tròn đến một chữ số thập phân).
- A \(6,0m.\)
- B \(16,6m.\)
- C \(7,5m.\)
- D \(5,0m.\)
Đáp án: C
Phương pháp giải:
- Áp dụng định lý Pytago trong tam giác vuông \(AHB\) tính \(BH\).
- Áp dụng hệ thức lượng trong tam giác vuông \(ABC\) tính \(BC\): \(A{B^2} = BH.BC\).
Lời giải chi tiết:
Ta có hình vẽ như sau:
Theo bài ra ta có: \(AD = 10m,\,\,\,CD = 1,5m\), góc “nâng” \(\angle BCH = {31^0}\) (với \(H\) là hình chiếu vuông góc của \(C\) lên \(AB\)).
Vì \(ADCH\) là hình chữ nhật nên \(CH = AD = 10m\), \(AH = CD = 1,5m\).
Xét tam giác vuông \(BCH\) có: \(BH = CH.\tan {31^0} = 10.\tan {31^0}\,\,\left( m \right)\).
Vậy chiều cao cột cờ là \(AB = AH + BH = 1,5 + 10.tan{31^0} \approx 7,5\,\,\left( m \right)\).
Chọn C.
Câu hỏi 2 :
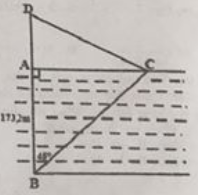
Tính chiều cao của một ngọn núi (làm tròn đến mét), biết tại hai điểm A, B cách nhau 500m, người ta nhìn thấy đỉnh núi với góc nâng lần lượt là 340 và 380. (Hình minh họa như hình bên)
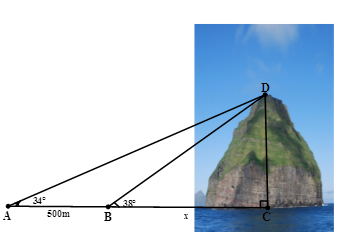
- A Chiều cao của ngọn núi là 2667,7 mét.
- B Chiều cao của ngọn núi là 2647,7 mét.
- C Chiều cao của ngọn núi là 2467,7 mét.
- D Chiều cao của ngọn núi là 2447,7 mét.
Đáp án: C
Lời giải chi tiết:

Đặt: BC = x (m)
\(AC = AB + BC = 500 + {x^{}}\left( m \right)\)
Xét tam giác vuông ACD, ta có:
\(\tan CAD = \dfrac{{CD}}{{AC}} \Rightarrow CD = AC.\tan CAD \Leftrightarrow CD = \left( {500 + x} \right).tan{34^0}\) (1)
Xét tam giác vuông BCD, ta có:
\(\tan CBD = \dfrac{{CD}}{{BC}} \Rightarrow CD = BC.\tan CBD \Leftrightarrow CD = x.tan{38^0}\) (2)
Từ (1) và (2)
\(\begin{array}{l}
\Rightarrow \left( {500 + x} \right).tan{34^0} = x.t{\rm{an3}}{8^0}\\
\Leftrightarrow 500.\tan {34^0} + x.tan{34^0} = x.\tan {38^0}\\
\Leftrightarrow x.\tan {38^0} - x.tan{34^0} = 500.\tan {34^0}\\
\Leftrightarrow x.\left( {tan{{38}^0} - tan{{34}^0}} \right) = 500.\tan {34^0}\\
\Leftrightarrow x = \dfrac{{500.\tan {{34}^0}}}{{tan{{38}^0} - tan{{34}^0}}} = 3158,5m
\end{array}\)
Chiều cao của ngọn núi là: \(CD = 3158,5.\tan {38^0} = 2467,{7^{}}\left( m \right)\)
Vậy: Chiều cao của ngọn núi là 2467,7 mét.
Câu hỏi 3 :
1. Một khối u của một căn bệnh nhân cách mặt da 5,7cm, được chiếu bởi một chùm tia gamma. Để tránh làm tổn thương mô, bác sĩ đặt nguồn tia cách khối u (trên mặt da) 8,3cm (hình vẽ)

1a) Hỏi góc tạo bởi chùm tia với mặt da?
1b) Chùm tia phải đi một đoạn dài bao nhiêu để đến được khối u?
2. Trước nhà thầy Tưởng có một cây cột điện cao 9m bị cơn bão Tembin vừa qua làm gãy ngang thân, ngọn cây cột điện chạm đất cách gốc 3m. Hỏi điểm gãy ngang của cây cột điện cách gốc bao nhiêu?

- A 1a) 34,50
1b)10,1cm
2) 5 mét
- B 1a) 34,50
1b)12,1cm
2) 4 mét
- C 1a) 34,50
1b) 10,1cm
2) 4 mét
- D 1a) 35,50
1b) 10,1cm
2) 6 mét
Đáp án: C
Lời giải chi tiết:
1.1a)
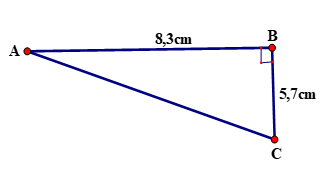
Đặt tên vị trí các điểm A, B, C như trong hình vẽ, trong đó:
AB = 8,3cm, BC = 5,7cm .
Đường đi của chùm tia tới khối u tương ứng với độ dài của đoạn AC trên hình, góc tạo bởi chùm tia với mặt da là góc BAC.
Xét tam giác vuông ABC, ta có:
\(\tan BAC=\frac{BC}{AB}=\frac{5,7}{8,3}\Rightarrow \angle BAC\approx 34,{{5}^{0}}\)
Vậy góc tạo bởi chùm tia với mặt da gần bằng 34,50
1.1b)
· Áp dụng định lý Pitago cho tam giác vuông ABC, ta có:
\(AC=\sqrt{A{{B}^{2}}+B{{C}^{2}}}=\sqrt{8,{{3}^{2}}+5,{{7}^{2}}}=\sqrt{101,38}\approx 10,1cm\)
Vậy Chùm tia phải đi một đoạn dài gần bằng 10,1cm để đến được khối u.
2. Vẽ lại hình minh họa và đặt tên các vị trí tương ứng như trong hình vẽ. Trong đó, AC’ = m là chiều cao cây cột điện, AC = 3m là khoảng từ ngọn cây cột điện chạm đất đến gốc cây, BC là cây cột điện bị gãy

AB là khoảng cách từ điểm gãy của cây cột điện đến gốc cây. Đặt AB = x (m), x > 0.
\(\Rightarrow BC'=BC=9-x\) (m)
Áp dụng định lý Pitago vào trong tam giác vuông ABC, ta có:
\(\begin{array}{l}A{B^2} + A{C^2} = B{C^2}\\ \Leftrightarrow {x^2} + {3^2} = {\left( {9 - x} \right)^2}\\ \Leftrightarrow {x^2} + 9 = 81 - 18x + {x^2}\\ \Leftrightarrow 18x = 72\\ \Leftrightarrow x = {4^{}}\left( {t/m} \right)\end{array}\)
Vậy điểm gãy ngang của cây cột điện cách gốc bằng 4 mét.
Câu hỏi 4 :
Hiện nay tại nước Mỹ quy định cầu thang cho người khuyết tật dùng xe lăn có hệ số góc không quá \(\frac{1}{12}\). Để phù hợp với tiêu chuẩn ấy thì chiều cao của cầu thang tối đa là bao nhiêu khi biết đáy cầu thang có độ dài là 4 m.
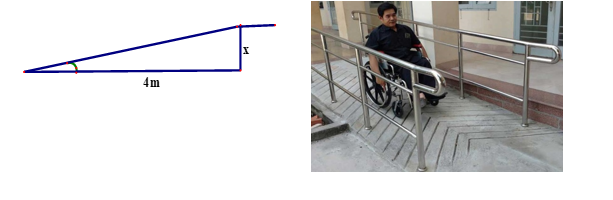
- A \(\frac{1}{3}\)mét.
- B \(\frac{2}{3}\)mét.
- C \(\frac{1}{4}\)mét.
- D \(\frac{3}{5}\)mét.
Đáp án: A
Lời giải chi tiết:
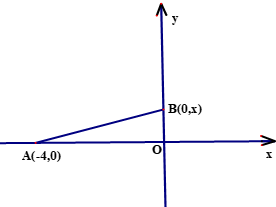 Gọi x là chiều cao của cầu thang Xét hệ tọa độ Oxy như hình vẽ với
Gọi x là chiều cao của cầu thang Xét hệ tọa độ Oxy như hình vẽ với
(0; 0); A (-4;0); B (0;x)
Hệ số góc của cầu thang là:
\(a=\operatorname{tanOAB}=\frac{OB}{OA}=\frac{x}{4}\)
Theo quy chuẩn thì:
\(a\le \frac{1}{12}\Leftrightarrow \frac{x}{4}\le \frac{1}{12}\Leftrightarrow x\le \frac{1}{3}\left( m \right)\)
Vậy chiều cao tối đa của cầu thang là \(\frac{1}{3}\)mét.
Câu hỏi 5 :
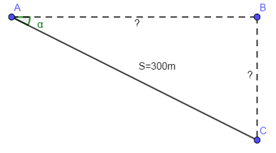
Tàu ngầm đang ở trên mặt biển bỗng đột ngột lặn xuống theo phương tạo với mặt nước biển một góc \({21^o}\). Nếu tàu chuyển động theo phương lặn xuống được 300m thì nó ở độ sâu bao nhiêu? Khi đó khoảng cách theo phương nằm ngang so với nơi xuất phát là bao nhiêu mét ? (kết quả làm tròn đến mét)
- A Tàu lặn xuống độ sâu 104 (m) và khoảng cách theo phương ngang từ vị trí ban đầu tới vị trí sau khi lặn là 260 (m)
- B Tàu lặn xuống độ sâu 109 (m) và khoảng cách theo phương ngang từ vị trí ban đầu tới vị trí sau khi lặn là 270 (m)
- C Tàu lặn xuống độ sâu 107 (m) và khoảng cách theo phương ngang từ vị trí ban đầu tới vị trí sau khi lặn là 280 (m)
- D Tàu lặn xuống độ sâu 119 (m) và khoảng cách theo phương ngang từ vị trí ban đầu tới vị trí sau khi lặn là 290 (m)
Đáp án: C
Phương pháp giải:
Áp dụng các công thức sin và cosin để tính các đại lượng đề bài yêu cầu
Lời giải chi tiết:
Coi mặt biển là một mặt phẳng, theo đề bài ta có hình vẽ minh họa:
Trong hình vẽ ta có:
+) Đoạn AC là quãng đường tàu di chuyển trong quá trình lặn,
+) Đoạn BC là độ sâu mà tàu lặn được.
+) Đoạn AB là khoảng cách theo phương ngang tính từ vị trí xuất phát tới vị trí của tàu sau khi lặn.
+) \(\alpha \) là góc tạo bởi quãng đường tàu chuyển động và mặt biển.
Xét tam giác vuông ABC vuông tại B có:
+) \(\sin \alpha = \frac{{BC}}{{AC}} \Rightarrow BC = AC.\sin \alpha = 300.\sin {21^o} \approx 107\left( m \right)\)
+) \(\cos \alpha = \frac{{AB}}{{AC}} \Rightarrow AB = AC.\cos \alpha = 300.cos{21^o} = 280\left( m \right)\)
Vậy tàu lặn xuống độ sâu 107 (m) và khoảng cách theo phương ngang từ vị trí ban đầu tới vị trí sau khi lặn là 280 (m).
Chọn C.
Câu hỏi 6 :
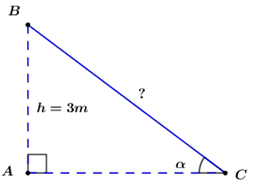
Nhà bạn Bình có gác lửng cao so với nền nhà là 3m. Ba bạn Bình cần đặt một thang đi lên gác, biết khi đặt thang phải để thang tạo được với mặt đất một góc \({70^o}\) thì đảm bảo sự an toàn khi sử dụng. Với kiến thức đã học, Bình hãy giúp Ba tính chiều dài thang là bao nhiêu mét để sử dụng. (kết quả làm tròn đến chữ số thập phân thứ hai)
- A \(4,24\)
- B \(2,34\)
- C \(2,34\)
- D \(3,19\)
Đáp án: D
Phương pháp giải:
Chiếc thang tạo với tường nhà một tam giác vuông với cạnh huyền chính là độ dài của thang. Áp dụng công thức sin vào tam giác vuông để tính độ dài cái thang
Lời giải chi tiết:
Ta có hình vẽ minh họa:
Như vậy độ dài cạnh BC chính là chiều dài của chiếc thang.
Xét tam giác ABC vuông tại A có:
\(\sin \alpha = \frac{{AB}}{{BC}} \Rightarrow BC = \frac{{AB}}{{\sin \alpha }} = \frac{3}{{\sin {{70}^o}}} = 3,19m\)
Vậy chiều dài của chiếc thang cần làm là \(3,19m\).
Chọn D.
Câu hỏi 7 :
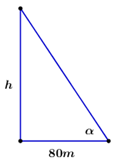
Một cột đèn cao \(7m\) có bóng trên mặt đất dài \(4m\).Gần đó có một tòa nhà cao tầng có bóng trên mặt đất dài \(80m\) (hình vẽ). Em hãy cho biết tòa nhà đó có bao nhiêu tầng, biết rằng mỗi tầng cao \(2m\).
- A \(80\) tầng
- B \(75\) tầng
- C \(70\) tầng
- D \(60\) tầng
Đáp án: C
Phương pháp giải:
+) Sử dụng các công thức lượng giác của một góc trong tam giác \(ABC\) vuông tại \(A\) có: \(\tan C = \frac{{AB}}{{AC}}.\)
+) Tính số tầng của tòa nhà = chiều cao của tòa nhà : chiều cao mỗi tầng.
Lời giải chi tiết:
Gọi \(h\) là chiều cao của tòa nhà cần tìm, \(\alpha \) là góc tia nắng mặt trời tạo với mặt đất lúc ấy.
Khi đó ta có: \(\tan \alpha = \frac{7}{4} = \frac{h}{{80}}\)
Suy ra: \(h = 140m\)
Vậy tòa nhà đó có: \(140:2 = 70\) (tầng)
Chọn C.
Câu hỏi 8 :
Tính chiều cao của một ngọn núi (làm tròn đến mét), biết tại hai điểm A, B cách nhau 500m , người ta nhìn thấy đỉnh núi với góc nắng lần lượt là \({34^o}\) và \({38^o}\).
- A \(2368m\)
- B \(1468m\)
- C \(3468m\)
- D \(2468m\)
Đáp án: D
Phương pháp giải:
Gọi CD vuông góc với AB với CD là chiều cao của ngọn núi. Áp dụng hệ thức lượng giác trong tam giác và dữ kiện đề bài cho để lập phương trình, tìm được độ cao ngọn núi.
Lời giải chi tiết:
Ta có hình vẽ minh họa

Xét tam giác vuông ADC vuông tại C có: \(\tan \left( {\angle DAC} \right) = \frac{{DC}}{{AC}} \Rightarrow AC = \frac{{DC}}{{\tan \left( {\angle DAC} \right)}}\).
Xét tam giác vuông BDC vuông tại C có: \(\tan \left( {\angle DBC} \right) = \frac{{DC}}{{BC}} \Rightarrow BC = \frac{{DC}}{{\tan \left( {\angle DBC} \right)}}\).
Có:
\(AC - BC = AB = 500\left( m \right) \Rightarrow \frac{{DC}}{{\tan \left( {\angle DAC} \right)}} - \frac{{DC}}{{\tan \left( {\angle DBC} \right)}} = 500\)
\( \Rightarrow DC.\left( {\frac{1}{{\tan {{34}^o}}} - \frac{1}{{\tan {{38}^o}}}} \right) = 500 \Rightarrow DC = \frac{{500}}{{\frac{1}{{\tan {{34}^o}}} - \frac{1}{{\tan {{38}^o}}}}} = 2468\left( m \right)\)
Vậy độ cao của ngọn núi là \(2468m\)
Chọn D
Câu hỏi 9 :
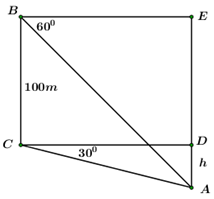
Trên quả đồi có một cái tháp cao \(100m\) . Từ đỉnh \(B\) và chân \(C\) của tháp nhìn điểm \(A\) ở chân đồi dưới các góc tương ứng bằng \({60^0}\) và \({30^0}\) so với phương nằm ngang (như hình vẽ). Chiều cao \(h\) của quả đồi là
- A \(h = 50m\)
- B \(h = 45m\)
- C \(h = 52m\)
- D \(h = 47m\)
Đáp án: A
Phương pháp giải:
Sử dụng các công thức tỉ số lượng giác của góc nhọn để làm bài toán.
Lời giải chi tiết:
Gọi \(AD = h\) là chiều cao của quả đồi.
Xét \(\Delta ACD\) vuông tại \(D\) ta có : \(\tan {30^0} = \frac{h}{{CD}} \Rightarrow h = CD.\tan {30^0} = \frac{{CD}}{{\sqrt 3 }}.\)
Xét \(\Delta ABE\) vuông tại \(E\) ta có : \(\tan {60^0} = \frac{{AE}}{{BE}} = \frac{{h + DE}}{{CD}}\)
\(\begin{array}{l} \Leftrightarrow CD.\tan {60^0} = h + BC \Leftrightarrow CD.\sqrt 3 = \frac{{CD}}{{\sqrt 3 }} + 100\\ \Leftrightarrow 3CD = CD + 100\sqrt 3 \Leftrightarrow CD = 50\sqrt 3 \,\,m.\\ \Rightarrow h = \frac{{CD}}{{\sqrt 3 }} = \frac{{50\sqrt 3 }}{{\sqrt 3 }} = 50\,\,m.\end{array}\)
Chọn A.
Câu hỏi 10 :
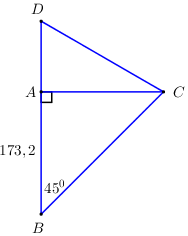
Từ nhà bạn An đến trường học, bạn phải đi đò qua một khúc sông rộng \(173,2m\) đến điểm A (bờ bên kia), rồi từ A đi bộ đến trường tại điểm D (ở hình bên). Thực tế, do nước chảy nên chiếc đò bị dòng nước đẩy xiên một góc \({45^0}\) đưa bạn tới điểm \(C\) (bờ bên kia). Từ C bạn An đi bộ đến trường theo đường CD mất thời gian gấp đôi khi đi từ A đến trường theo đường AD. Độ dài quãng đường CD là
(Giả sử rằng vận tốc đi bộ của bạn An không thay đổi (chuyển động thẳng đều), kết quả làm tròn đến hàng đơn vị).
- A \(190m\)
- B \(220m\)
- C \(200m\)
- D \(210m\)
Đáp án: C
Phương pháp giải:
Sử dụng các tỉ số lượng giác của góc nhọn trong tam giác vuông.
Lời giải chi tiết:
Dễ thấy tam giác \(ABC\) vuông cân tại \(A \Rightarrow AC = AB = 173,2\,\,\left( m \right)\).
Do từ C bạn An đi bộ đến trường theo đường CD mất thời gian gấp đôi khi từ từ A đến trường theo đường AB nên quãng đường CD gấp đôi quãng đường AD \( \Rightarrow CD = 2AD\).
Xét tam giác vuông \(ACD\) có: \(\sin \angle ACD = \frac{{AD}}{{CD}} = \frac{1}{2} \Rightarrow \angle ACD = {30^0}\).
\( \Rightarrow CD = \frac{{AC}}{{\cos {{30}^0}}} = \frac{{173,2}}{{\cos {{30}^0}}} \approx 200\,\,\left( m \right)\)
Chọn C.
Câu hỏi 11 :
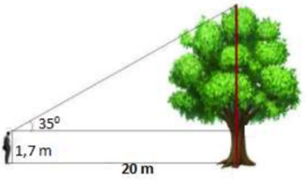
Tính chiều cao của cây trong hình vẽ bên (Làm tròn đến chữ số thập phân thứ nhất)
- A \(14,3m\)
- B \(15,7m\)
- C \(16,8m\)
- D \(17,2m\)
Đáp án: B
Phương pháp giải:
Sử dụng giá trị lượng giác của một góc nhọn trong tam giác vuông để giải tam giác.
Lời giải chi tiết:
Chiều cao của cây là : \(h = 1,7 + 20.\tan 35^\circ \approx 15,7m\).
Chọn B.
Câu hỏi 12 :
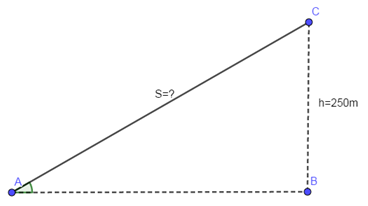
Một máy bay cất cánh theo phương có góc nâng là \({23^o}\)so với mặt đất. Hỏi muốn đạt độ cao 250m so với mặt đất thì máy bay phải bay lên một đoạn đường là bao nhiêu mét? (làm tròn đến mét)
- A 640 (m)
- B 650 (m)
- C 660 (m)
- D 670 (m)
Đáp án: A
Phương pháp giải:
Góc nâng của máy bay là góc tạo bởi hướng chuyển động bay lên của may bay với phương nằm ngang của mặt đất. Từ đó áp dụng công thức sin để tính đoạn đường mà máy bay cần bay để đạt độ cao 250m.
Lời giải chi tiết:
Ta có hình vẽ minh họa.
Độ dài đoạn AC chính là quãng đường máy bay cần đi để đạt độ cao 250m.
Xét tam giác ABC vuông tại B có:
\(\sin \left( {\angle CAB} \right) = \frac{{BC}}{{AC}} \Rightarrow AC = \frac{{BC}}{{\sin \left( {\angle CAB} \right)}} = \frac{h}{{\sin {{23}^o}}} = \frac{{250}}{{\sin {{23}^o}}} \approx 640\left( m \right)\)
Vậy máy bay cần bay quãng đường 640 (m) để đạt được độ cao 250 (m).
Chọn A.
Câu hỏi 13 :
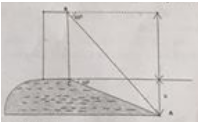
Vào khoảng năm 200 trước Công nguyên, Ơ-ra-tô-xten, một nhà toán học và thiên văn học Hi lạp đã ước lượng được "chu vi" của Trái Đất (chu vi đường xích đạo) nhờ hai quan sát sau:
a) Một ngày trong năm, ông để ý thấy Mặt Trời chiếu thẳng các đáy giếng ở thành phố Xy-en (nay gọi là Át-xu-an), tức là tia sáng chiếu thẳng đứng
b) Cùng lúc đó ở thành phố A-lếch-xăng-đri-a cách Xy-en 800km, một tháp cao 25m có bóng trên mặt đất dài 3,1m
Từ hai quan sát trên, em hãy tính xấp xỉ "chu vi" của Trái Đất (Trên hình), điểm S tượng trưng cho thành phố Xy-en, điểm A tượng trưng cho thành phố A-lếch-xăng-đri-a, bóng của tháp trên mặt đất được coi là đoạn thẳng AB

- A 407,41km
- B 407410km
- C 40,741km
- D 40741km
Đáp án: D
Lời giải chi tiết:
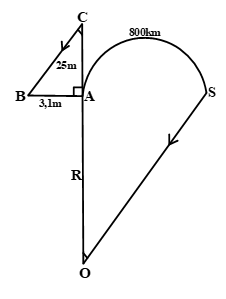
Do cung AB quá nhỏ (3,1m) nên ta có thể xem như là một đoạn thẳng.
trong tam giác vuông ABC, ta có:
\(\tan \widehat {ACB} = \dfrac{{AB}}{{AC}} = \dfrac{{3,1}}{{25}} = 0,124 \Rightarrow \widehat {ACB} \approx 7,{069^0}\)
Do các tia sáng đến từ mặt trời coi như song song nên ta có:CB // SO
Suy ra: \(\widehat {ACB} = \widehat {AOS} \approx 7,{069^0}\) (hai góc so le trong)
Ta có:Độ dài cung AS = 800km ứng với góc 7,0690 ở tâm
Chu vi Trái Đất P ứng với góc 3600
Suy ra, chu vi của Trái Đất là:
\(P = \dfrac{{360.800}}{{7,069}} \approx {40741^{}}\left( {km} \right)\)
Câu hỏi 14 :
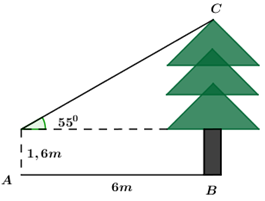
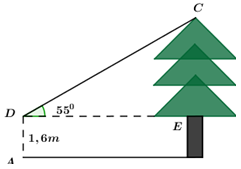
Bạn Thanh đứng tại vị trí \(A\) cách cây thông \(6m\) và nhìn thấy ngọn của cây này duwosi một góc bằng \({55^0}\) so với phương nằm ngang (như hình vẽ). Biết khoảng cách từ mắt của bạn Thanh đến mặt đất bằng \(1,6m.\) Chiều cao \(BC\) của cây thông bằng (làm tròn đến số thập phân thứ hai):
- A \(5,80m\)
- B \(8,57m\)
- C \(6,51m\)
- D \(10,17m\)
Đáp án: D
Phương pháp giải:
Sử dụng tỉ số lượng giác của góc nhọn trong tam giác vuông để làm bài.
Lời giải chi tiết:
Đặt các điểm \(D,\,\,E\) như hình vẽ.
Xét \(\Delta CDE\) vuông tại \(E\) ta có:
\(CE = DE.\tan {55^0} = 6.\tan {55^0} \approx 8,57\,m.\)
\( \Rightarrow \) Chiều cao của cây là: \(BC = CE + BE = 8,57 + 1,6 = 10,17\,\,m.\)
Chọn D.
Câu hỏi 15 :
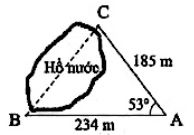
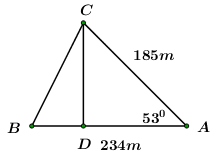
Tính khoảng cách giữa hai điểm \(B\) và \(C,\) biết rằng từ vị trị \(A\) ta đo được \(AB = 234\,m,\,\,\,AC = 185\,m\) và \(\angle BAC = {53^0}\) (kết quả tính bằng mét và làm tròn đến hàng đơn vị).
- A \(190m\)
- B \(191m\)
- C \(192m\)
- D \(193m\)
Đáp án: C
Phương pháp giải:
Từ \(C,\) dựng đường vuông góc với \(AB,\) cắt \(AB\) tại \(D.\)
Khi đó ta có: \(CD\) là đường cao của \(\Delta ABC.\)
Áp dụng tỉ số lượng giác của góc nhọn trong
\(\Delta ACD\) vuông tại \(D\) ta có:
\(\begin{array}{l}\sin \angle A = \frac{{CD}}{{CA}} \Rightarrow CD = CA.\sin \angle A\\\cos \angle A = \frac{{AD}}{{AC}} \Rightarrow AD = CA.\cos \angle A\\ \Rightarrow BD = AB - AD.\end{array}\)
Áp dụng định lý Pitago cho \(\Delta BCD\) để tính \(BC.\)
Lời giải chi tiết:
Từ \(C,\) dựng đường vuông góc với \(AB,\) cắt \(AB\) tại \(D.\)
Khi đó ta có: \(CD\) là đường cao của \(\Delta ABC.\)
Áp dụng tỉ số lượng giác của góc nhọn trong
\(\Delta ACD\) vuông tại \(D\) ta có:
\(\begin{array}{l}\sin \angle A = \frac{{CD}}{{CA}} \Rightarrow CD = CA.\sin \angle A\\ \Rightarrow CD = 185.\sin {53^0}.\\\cos \angle A = \frac{{AD}}{{AC}} \Rightarrow AD = CA.\cos \angle A\\ \Rightarrow AD = 185.\cos {53^0}.\\ \Rightarrow BD = AB - AD = 234 - 185.\cos {53^0}.\end{array}\)
Áp dụng định lý Pitago cho \(\Delta BCD\) để tính \(BC.\)
\(\begin{array}{l}B{C^2} = B{D^2} + C{D^2} = {\left( {234 - 185.\cos {{53}^0}} \right)^2} + {\left( {185.\sin {{53}^0}} \right)^2}\\ \Leftrightarrow B{C^2} = {234^2} - 2.234.185\cos {53^0} + {\left( {185.\cos {{53}^0}} \right)^2} + {\left( {185.\sin {{53}^0}} \right)^2}\\ \Leftrightarrow B{C^2} = {234^2} - 2.234.185\cos {53^0} + {185^2}\\ \Leftrightarrow B{C^2} \approx 36875,86\\ \Rightarrow BC \approx 192\,m.\end{array}\)
Chọn C.
>> Học trực tuyến lớp 9 và Lộ trình UP10 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Lộ trình học tập 3 giai đoạn: Học nền tảng lớp 9, Ôn thi vào lớp 10, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
 |
 |
 |
 |
 |
 |
Các bài khác cùng chuyên mục