Đề tham khảo thi vào 10 môn Toán TP Hồ Chí Minh năm 2025 - Đề số 6

Đề bài

Câu 1 (1,5 điểm): Cho parabol \((P)\,\,:y = \,\frac{1}{2}{x^2}\).

a) Vẽ \((P)\) trên mặt phẳng tọa độ \({\rm{Ox}}y\).

b) Tìm giá trị của m để điểm \(A\left( {m;{m^3}} \right)\) thuộc (P).

Câu 2 (1 điểm): Cho phương trình \(3{x^2} - 5x - 4 = 0\)

a) Chứng minh phương trình có 2 nghiệm phân biệt.

b) Hãy tính giá trị của biểu thức \(P = {x_1}\left( {{x_1} - 12} \right) + {x_2}\left( {{x_2} - 12} \right)\).

Câu 3 (1,5 điểm): Biểu đồ cột kép ở hình sau biểu diễn số lượng học sinh tham gia giải thi đấu thể thao của trường THCS A.

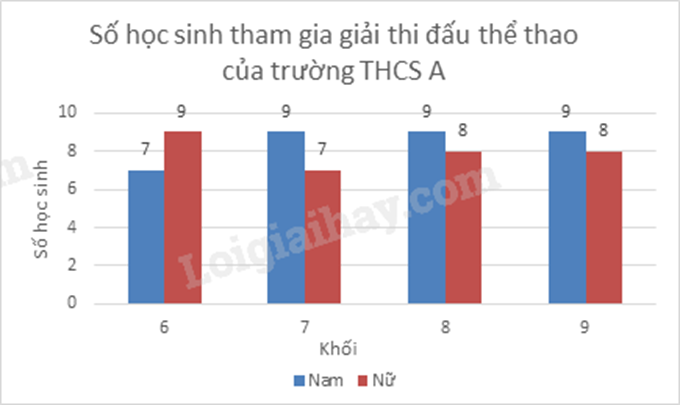
a) Tính tổng số học sinh của trường THCS A tham gia giải thi đấu thể thao.

b) Chọn ngẫu nhiên một học sinh tham gia giải thi đấu thể thao của trường đó. Tính xác suất của mỗi biến cố sau:

A: “Học sinh được chọn là nam”.

B: “Học sinh được là nữ và không thuộc khối 9”.

Câu 4 (1 điểm): Một hình hộp không có nắp được làm từ một mảnh bìa giấy theo như hình vẽ. Hộp có đáy là một hình vuông cạnh \(x\) cm, chiều cao \(h = 10\)cm.

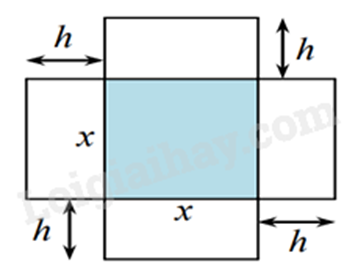
a) Viết công thức A biểu diễn theo \(x\) diện tích xung quanh của chiếc hộp.

b) Biết rằng tổng diện tích xung quanh và diện tích đáy của chiếc hộp là \(225c{m^2}\). Tính độ dài cạnh đáy chiếc hộp.

Câu 5 (1 điểm): Vừa qua trên mạng xã hội, nhiều người truyền tai nhau hình ảnh về một hiện tượng tự nhiên vô cùng kỳ lạ, xuất hiện vào sáng ngày 24/11/2022. Được biết, bức ảnh này được chụp lại núi Bà Đen, một địa điểm du lịch vô cùng nổi tiếng của Tây Ninh.

Trong hình ảnh, đỉnh núi được bao phủ bởi một lớp mây trắng xóa. Không chỉ có vậy, những đám mây còn tạo thành một lớp "vỏ" có phần kỳ bí. Nhiều người gọi đây là hiện tượng "mây vờn", có người nhận xét trông đám mây như một chiếc nón. Ước tính chiều cao của nón lớn là \(200\,m\), bán kính đáy của nón lớn là \(300\,m\), độ dày đám mây là \(l = 20\,m\). Với \(1\,{m^3}\) mây chứa \(0,5\) gam nước. Hỏi đám mây trên chứa bao nhiêu kilôgam nước? (làm tròn đến hàng đơn vị của kilôgam) Biết thể tích hình nón là \(V = \frac{1}{3}\pi {R^2}h\) (trong đó\(R\) là bán kính đường tròn đáy; \(h\) là chiều cao hình nón, lấy \(\pi  \approx 3,14\)). Giả sử phần núi bị bao phủ cũng là một hình nón.

Câu 6 (1 điểm): Một xí nghiệp dự tính chuyển hàng bằng hai xe tải và đang phân vân giữa việc mua hẳn hai chiếc xe tải hoặc thuê hai xe tải. Nếu mua hai xe với giá mỗi xe là 200 triệu đồng thì mỗi ngày xí nghiệp phải tốn 5 triệu đồng cho tất cả tài xế và nhiên liệu. Còn nếu thuê xe thì giá thuê một xe tải là 10 triệu đồng/ngày (đã bao gồm tiền công cho tài xế và nhiên liệu).

a) Trong trường hợp xí nghiệp quyết định mua và xe tải mới mua cần phải bảo dưỡng định kì, xí nghiệp sẽ sử dụng kết hợp cả xe tải mua và xe tải thuê. Khi đó, tổng chi phí vận chuyển cho một đợt chuyển hàng 300 ngày là 4 tỉ đồng (bao gồm cả tiền mua xe). Hãy tính số ngày sử dụng xe tải mua và số ngày sử dụng xe tải thuê trong đợt chuyển hàng này.

b) Trong trường hợp xí nghiệp vẫn đang phân vân giữa việc mua xe và thuê xe thì sau bao nhiêu ngày phương án mua xe sẽ tiết kiệm hơn phương án thuê xe?

Câu 7 (3 điểm): Cho đường tròn \(\left( {O;R} \right)\) đường kính \(AB\). Trên tiếp tuyến tại \(A\), lấy \(M\) sao cho \(AM = 2R\), \(MB\) cắt đường tròn \(\left( O \right)\) tại \(C\).

a) Kẻ \(AH \bot OM\) tại H. Chứng minh tứ giác \(AMCH\) nội tiếp.

b) Chứng minh \(M{A^2} = MB.MC\) và \(\frac{{MB}}{{MC}} = \frac{{A{B^2}}}{{A{C^2}}}\).

c) Chứng minh \(HB \bot HC\) và tính diện tích tứ giác \(BCHO\) theo \(R\).

-------- HẾT --------

Lời giải

Câu 1 (1,5 điểm): Cho parabol \((P)\,\,:y = \,\frac{1}{2}{x^2}\).

a) Vẽ \((P)\) trên mặt phẳng tọa độ \({\rm{Ox}}y\).

b) Tìm giá trị của m để điểm \(A\left( {m;{m^3}} \right)\) thuộc (P).

Phương pháp

a) Lập bảng giá trị, vẽ đồ thị hàm số trên hệ trục tọa độ.

b) Thay toạ độ điểm m vào (P) và giải phương trình để tìm m.

Lời giải

a) Ta có bảng giá trị sau:

Đồ thị hàm số là đường cong parabol đi qua các điểm \(O\,\left( {0;0} \right);A\left( { - 2;2} \right);B\left( { - 1;\frac{1}{2}} \right);\,\,C\left( {1;\frac{1}{2}} \right);\,\,D\left( {2;2} \right)\)

Ta vẽ được đồ thị hàm số \(y = \frac{1}{2}{x^2}\) như sau:

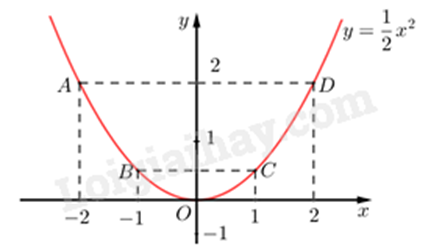
b) Vì \(A\left( {m;{m^3}} \right) \in \left( P \right)\) nên ta có:

\(\begin{array}{l}{m^3} = \frac{1}{2}{m^2}\\{m^3} - \frac{1}{2}{m^2} = 0\\{m^2}\left( {m - \frac{1}{2}} \right) = 0\end{array}\)

\({m^2} = 0\) hoặc \(m - \frac{1}{2} = 0\)

\(m = 0\) (TM) hoặc \(m = \frac{1}{2}\) (TM)

Vậy \(m = 0\); \(m = \frac{1}{2}\) thì điểm \(A\left( {m;{m^3}} \right)\) thuộc (P).

Câu 2 (1 điểm): Cho phương trình \(3{x^2} - 5x - 4 = 0\)

a) Chứng minh phương trình có 2 nghiệm phân biệt.

b) Hãy tính giá trị của biểu thức \(P = {x_1}\left( {{x_1} - 12} \right) + {x_2}\left( {{x_2} - 12} \right)\).

Phương pháp

a) Sử dụng \(ac < 0\) để chứng minh phương trình có hai nghiệm phân biệt.

b) Áp dụng định lí Viète và biến đổi P để xuất hiện tổng và tích của hai nghiệm.

Định lí Viète: \({x_1} + {x_2} = \frac{{ - b}}{a};{x_1}{x_2} = \frac{c}{a}\).

Lời giải

a) Ta có: \(a = 3,{\rm{ }}b =  - 5,{\rm{ }}c =  - 4\)

Vì \(a.c = 3.\left( { - 4} \right) =  - 12 < 0\) nên phương trình luôn có hai nghiệm phân biệt \({x_1}{\mkern 1mu} ;{\mkern 1mu} {x_2}\).

b) Theo định lí Viète, ta có: \({x_1} + {x_2} =  - \frac{b}{a} =  - \frac{{ - 5}}{3} = \frac{5}{3};{x_1}{x_2} = \frac{c}{a} = \frac{{ - 4}}{3}\).

Ta có:

\(\begin{array}{l}P = {x_1}\left( {{x_1} - 12} \right) + {x_2}\left( {{x_2} - 12} \right)\\ = x_1^2 - 12{x_1} + x_2^2 - 12{x_2}\\ = {x_1}^2 + {x_2}^2 - 12\left( {{x_1} + {x_2}} \right)\\{\mkern 1mu}  = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} - 12\left( {{x_1} + {x_2}} \right)\\{\mkern 1mu}  = {\left( {\frac{5}{3}} \right)^2} - 2.\left( {\frac{{ - 4}}{3}} \right) - 12.\frac{5}{3} =  - \frac{{131}}{9}\end{array}\)

Vậy \(P =  - \frac{{131}}{9}\).

Câu 3 (1,5 điểm): Biểu đồ cột kép ở hình sau biểu diễn số lượng học sinh tham gia giải thi đấu thể thao của trường THCS A.

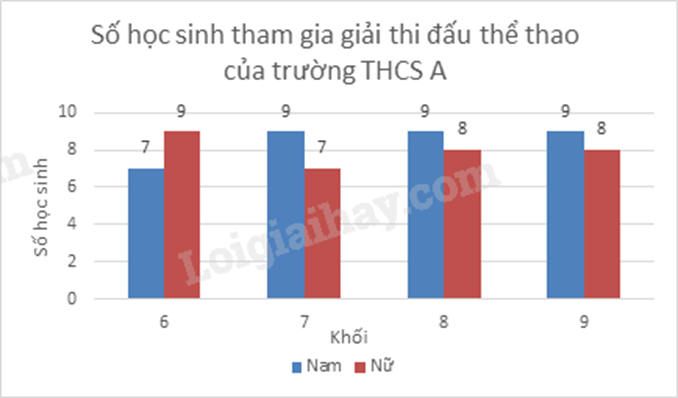
a) Tính tổng số học sinh của trường THCS A tham gia giải thi đấu thể thao.

b) Chọn ngẫu nhiên một học sinh tham gia giải thi đấu thể thao của trường đó. Tính xác suất của mỗi biến cố sau:

A: “Học sinh được chọn là nam”.

B: “Học sinh được là nữ và không thuộc khối 9”.

Phương pháp

a) Tổng số học sinh của trường tham gia giải thi đấu thể thao bằng tổng số học sinh 4 khối tham gia.

b) Xác định số kết quả thuận lợi cho biến cố.

Xác suất của biến cố bằng tỉ số giữa số kết quả thuận lợi và số phần tử của không gian mẫu (tổng số học sinh của trường).

Lời giải

a) Nhìn vào biểu đồ ta thấy:

- Lớp 6 có tất cả: 7 nam + 9 nữ = 16 (học sinh)

- Lớp 7 có tất cả: 9 nam + 7 nữ = 16 (học sinh)

- Lớp 8 có tất cả: 9 nam + 8 nữ = 17 (học sinh)

- Lớp 9 có tất cả: 9 nam + 8 nữ = 17 (học sinh)

Tổng số học sinh của trường THCS A tham gia giải thi đấu thể thao là:

16 + 16 + 17 + 17 = 66 (học sinh)

Vậy có 66 học sinh của trường THCS A tham gia giải thi đấu thể thao.

b) Số kết quả thuận lợi cho biến cố A: “Học sinh được chọn là nam” là:

7 + 9 + 9 + 9 = 34 (học sinh)
Xác suất để biến cố A xảy ra là: \(P\left( A \right) = \frac{{34}}{{66}} = \frac{{17}}{{33}}\).

Số kết quả thuận lợi cho biến cố B: “Học sinh được là nữ và không thuộc khối 9” là:

9 + 7 + 8 = 24 (học sinh)

Xác suất để biến cố B xảy ra là: \(P\left( B \right) = \frac{{24}}{{66}} = \frac{4}{{11}}\).

Câu 4 (1 điểm): Một hình hộp không có nắp được làm từ một mảnh bìa giấy theo như hình vẽ. Hộp có đáy là một hình vuông cạnh \(x\) cm, chiều cao \(h = 10\)cm.

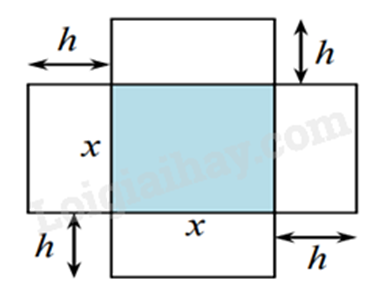
a) Viết công thức A biểu diễn theo \(x\) diện tích xung quanh của chiếc hộp.

b) Biết rằng tổng diện tích xung quanh và diện tích đáy của chiếc hộp là \(225c{m^2}\). Tính độ dài cạnh đáy chiếc hộp.

Phương pháp

Hình hộp không có nắp:

- Đáy là hình vuông cạnh \(x\) cm

- Chiều cao \(h = 10\) cm

a) Sử dụng công thức tính diện tích xung quanh của hình hộp chữ nhật: \({S_{xq}} = \) Chu vi đáy. chiều cao.

b) Viết phương trình biểu diễn tổng diện tích xung quanh và diện tích đáy của chiếc hộp. Từ đó tìm cạnh đáy \(x\) của chiếc hộp.

Lời giải
Diện tích xung quanh của chiếc hộp là:

${{S}_{xq}}={{C}_{\text{đáy}}}.h=4x.10=40x\left( c{{m}^{2}} \right)$

Vậy \(A = 40x\).

b) Điều kiện: \(x \in {N^*}\).

Diện tích đáy của chiếc hộp là: ${{S}_{\text{đáy}}}={{x}^{2}}$

Vì tổng diện tích xung quanh và diện tích đáy của chiếc hộp là \(225c{m^2}\) nên ta có phương trình:

\(40x + {x^2} = 225\)

\({x^2} + 40x - 225 = 0\)

Ta có: \(a = 1;b' = \frac{b}{2} = \frac{{40}}{2} = 20;c =  - 225\).

Do đó \(\Delta ' = {20^2} - 1 \cdot ( - 225) = 400 + 225 = 625 > 0\) nên phương trình có hai nghiệm phân biệt \({x_1} =  - 20 - \sqrt {625}  =  - 45\left( L \right);{x_2} =  - 20 + \sqrt {625}  = 5\left( {TM} \right)\)

Vậy độ dài cạnh đáy là \(5{\rm{cm}}\).

Câu 5 (1 điểm): Vừa qua trên mạng xã hội, nhiều người truyền tai nhau hình ảnh về một hiện tượng tự nhiên vô cùng kỳ lạ, xuất hiện vào sáng ngày 24/11/2022. Được biết, bức ảnh này được chụp lại núi Bà Đen, một địa điểm du lịch vô cùng nổi tiếng của Tây Ninh.

Trong hình ảnh, đỉnh núi được bao phủ bởi một lớp mây trắng xóa. Không chỉ có vậy, những đám mây còn tạo thành một lớp "vỏ" có phần kỳ bí. Nhiều người gọi đây là hiện tượng "mây vờn", có người nhận xét trông đám mây như một chiếc nón. Ước tính chiều cao của nón lớn là \(200\,m\), bán kính đáy của nón lớn là \(300\,m\), độ dày đám mây là \(l = 20\,m\). Với \(1\,{m^3}\) mây chứa \(0,5\) gam nước. Hỏi đám mây trên chứa bao nhiêu kilôgam nước? (làm tròn đến hàng đơn vị của kilôgam) Biết thể tích hình nón là \(V = \frac{1}{3}\pi {R^2}h\) (trong đó\(R\) là bán kính đường tròn đáy; \(h\) là chiều cao hình nón, lấy \(\pi  \approx 3,14\)). Giả sử phần núi bị bao phủ cũng là một hình nón.

Phương pháp

Hình nón lớn bao gồm thể tích của phần núi bị bao phủ bởi mây (hình nón nhỏ) và thể tích đám mây.

Sử dụng công thức tính thể tích hình nón để tính thể tích hình nón lớn, hình nón nhỏ.

Từ đó tính được thể tích đám mây = thể tích hình nón lớn – thể tích hình nón nhỏ.

Lượng nước mà đám mây có thể chứa = thể tích đám mây. 0,5 (g)

Đổi đơn vị về kg.

Lời giải

Hình nón lớn bao gồm thể tích của phần núi bị bao phủ bởi mây (hình nón nhỏ) và thể tích đám mây.

Thể tích hình nón lớn là:

\({V_1} = \frac{1}{3}\pi {R^2}h \approx \frac{1}{3}.3,{14.300^2}.200 = 18\,840\,000\,\left( {{m^3}} \right)\)

Bán kính đáy của hình nón nhỏ là: \(300 - 20 = 280\left( m \right)\)

Chiều cao của hình nón nhỏ là: \(200 - 20 = 180\left( m \right)\)

Thể tích hình nón nhỏ là: \({V_2} = \frac{1}{3}\pi {r^2}h \approx \frac{1}{3}.3,{14.280^2}.180 = 14\,770\,560\,\,\left( {{m^3}} \right)\)

Thể tích đám mây là: \(V = {V_1} - {V_2} = 18\,840\,000 - 14\,770\,560 = 4\,069\,440\,\,\left( {{m^3}} \right)\)

Lượng nước mà đám mây có thể chứa

\(V = 4\,069\,440.0,5 = 2\,034\,720\,\left( g \right) \approx 2\,035\left( {kg} \right)\)

Vậy lượng nước mà đám mây có thể chứa khoảng \(2035\) kilôgam.

Câu 6 (1 điểm): Một xí nghiệp dự tính chuyển hàng bằng hai xe tải và đang phân vân giữa việc mua hẳn hai chiếc xe tải hoặc thuê hai xe tải. Nếu mua hai xe với giá mỗi xe là 200 triệu đồng thì mỗi ngày xí nghiệp phải tốn 5 triệu đồng cho tất cả tài xế và nhiên liệu. Còn nếu thuê xe thì giá thuê một xe tải là 10 triệu đồng/ngày (đã bao gồm tiền công cho tài xế và nhiên liệu).

a) Trong trường hợp xí nghiệp quyết định mua và xe tải mới mua cần phải bảo dưỡng định kì, xí nghiệp sẽ sử dụng kết hợp cả xe tải mua và xe tải thuê. Khi đó, tổng chi phí vận chuyển cho một đợt chuyển hàng 300 ngày là 4 tỉ đồng (bao gồm cả tiền mua xe). Hãy tính số ngày sử dụng xe tải mua và số ngày sử dụng xe tải thuê trong đợt chuyển hàng này.

b) Trong trường hợp xí nghiệp vẫn đang phân vân giữa việc mua xe và thuê xe thì sau bao nhiêu ngày phương án mua xe sẽ tiết kiệm hơn phương án thuê xe?

Phương pháp

a) Gọi số ngày sử dụng xe tải mua và số ngày sử dụng xe tải thuê lần lượt là \(x\) và \(y\) (đơn vị: ngày), điều kiện: \(x,y \in {\mathbb{N}^*}\) và \(x,y < 300\).

Viết phương trình biểu diễn tổng số ngày vận chuyển.

Chi phí sử dụng xe mua = chi phí mua 2 xe + chi phí \(x\) ngày xí nghiệp tốn cho tất cả tài xế và nghiên liệu.

Chi phí sử dụng xe thuê = 2. chi phí thuê xe trong \(y\) ngày (vì thuê 2 xe).

Từ đó viết phương trình biểu diễn tổng chi phí vận chuyển cho 300 ngày.

Lập hệ phương trình, giải hệ phương trình tìm được.

Kiểm tra lại điều kiện của \(x,y\).

b) Gọi số ngày chuyển hàng là n \(\left( {n \in {\mathbb{N}^*}} \right)\).

Tính chi phí theo phương án mua xe, thuê xe.

Lập bất phương trình biểu diễn: chi phí phương án mua xe < chi phí phương án thuê xe.

Giải bất phương trình để tìm n.

Lời giải

a) Gọi số ngày sử dụng xe tải mua và số ngày sử dụng xe tải thuê lần lượt là \(x\) và \(y\) (đơn vị: ngày), điều kiện: \(x,y \in {\mathbb{N}^*}\) và \(x,y < 300\).

Vì tổng số ngày sử dụng xe tải mua và số ngày sử dụng xe tải thuê là 300 ngày nên ta có phương trình: \(x + y = 300\). (1)

Chi phí sử dụng xe tải mua (bao gồm cả tiền mua xe) là: \(2.200 + 5x = 400 + 5x\) (đồng)

Chi phí sử dụng xe tải thuê là: \(2.10y = 20y\) (đồng)

Vì tổng chi phí vận chuyển là 4 tỉ đồng = 4 000 triệu đồng (bao gồm cả tiền mua xe) nên ta có phương trình:

\(400 + 5x + 20y = 4000\) hay \(5x + 20y = 3600\). (2)

Từ (1) và (2) ta có hệ phương trình: \(\left\{ {\begin{array}{*{20}{l}}{x + y = 300}\\{5x + 20y = 3600}\end{array}} \right.\).

Giải hệ phương trình, ta được \(\left\{ {\begin{array}{*{20}{l}}{x = 160}\\{y = 140}\end{array}} \right.\) (TM)

Vậy xí nghiệp sử dụng xe tải mua 160 ngày và xe tải thuê 140 ngày.

b) Gọi số ngày chuyển hàng là n \(\left( {n \in {\mathbb{N}^*}} \right)\).

Chi phí sử dụng xe mua (bao gồm cả tiền mua xe) sau n ngày là: \(2.200 + 5n = 400 + 5n\) (triệu đồng)

Chi phí sử dụng xe thuê sau n ngày là: \(2.10.n = 20n\) (triệu đồng)

Phương án mua xe sẽ tiết kiệm hơn phương án thuê xe khi:

\(\begin{array}{l}400 + 5n < 20n\\400 < 15n\\n > 26,67\end{array}\)

Suy ra \(n \ge 27\)

Vậy sau 27 ngày thì phương án mua xe sẽ tiết kiệm hơn phương án thuê xe.

Câu 7 (3 điểm): Cho đường tròn \(\left( {O;R} \right)\) đường kính \(AB\). Trên tiếp tuyến tại \(A\), lấy \(M\) sao cho \(AM = 2R\), \(MB\) cắt đường tròn \(\left( O \right)\) tại \(C\).

a) Kẻ \(AH \bot OM\) tại H. Chứng minh tứ giác \(AMCH\) nội tiếp.

b) Chứng minh \(M{A^2} = MB.MC\) và \(\frac{{MB}}{{MC}} = \frac{{A{B^2}}}{{A{C^2}}}\).

c) Chứng minh \(HB \bot HC\) và tính diện tích tứ giác \(BCHO\) theo \(R\).

Phương pháp

a) Chứng minh \(\Delta MAC\) và \(\Delta MAH\) nội tiếp đường tròn đường kính AM, suy ra A, M, C, H cùng thuộc đường tròn đường kính AM nên tứ giác AMCH nội tiếp.

b) Chứng minh \(M{A^2} = MB.MC\)

Chứng minh \(\Delta MAC\,\backsim \,\Delta MBA\) (g.g) suy ra tỉ số bằng nhau giữa các cặp cạnh tương ứng.

Chứng minh  \(\frac{{MB}}{{MC}} = \frac{{A{B^2}}}{{A{C^2}}}\)

Chứng minh \(\Delta ABM\) vuông cân tại A nên AC vừa là đường cao vừa là đường trung tuyến

Suy ra \(\frac{{MB}}{{MC}} = 2\)

Sử dụng tính chất đường trung tuyến ứng với cạnh huyền suy ra \(AB = CB\)

Áp dụng định lí Pythagore vào \(\Delta CAB\) vuông cân tại C suy ra \(\frac{{A{B^2}}}{{A{C^2}}} = 2\)

Do đó \(\frac{{MB}}{{MC}} = \frac{{A{B^2}}}{{A{C^2}}} = 2\)

c) Chứng minh \(HB \bot HC\)

Áp dụng định lí Pythagore vào \(\Delta AOM\) vuông tại A để tính cạnh huyền OM.

Chứng minh \(\Delta \,HOA\backsim \,\Delta AOM\) (g. g) suy ra tỉ số bằng nhau giữa các cặp cạnh tương ứng để tính \(HA\) theo R.

Chứng minh \(\Delta \,AOM\backsim \,\Delta HAM\) (g. g) suy ra tỉ số bằng nhau giữa các cặp cạnh tương ứng để tính \(HM\) theo R.

Do đó \(\Delta \,HOA\backsim \,\Delta HAM\)

Chứng minh \(\frac{{HA}}{{HM}} = \frac{{AC}}{{MB}}\)

Suy ra \(\Delta \,MHB\backsim \,\Delta AHC\) (c.g.c) suy ra \(\widehat {MHB} = \widehat {AHC}\) (cặp góc tương ứng)

Hai góc có chung góc MHC nên \(\widehat {CHB} = \widehat {AHM} = 90^\circ \)

suy ra \(HB \bot HC\)

Tính diện tích tứ giác \(BCHO\) theo \(R\)

Từ H kẻ \(HE \bot AO\)

Chứng minh \({S_{\Delta HOA}} = {S_{\Delta HOB}}\)

Vì \(\Delta \,HOA\backsim \,\Delta AOM\) (cmt) suy ra tỉ số diện tích hai tam giác đồng dạng \({S_{\Delta HOA}}\) và \({S_{\Delta AOM}}\)

Áp dụng định lí Pythagore vào \(\Delta ABC\) vuông cân tại C để tính BC.

Chứng minh \(\widehat {HAB} = \widehat {HBC}\)

Suy ra chứng minh \(\Delta \,HAO\backsim \,\Delta HBC\) (g.g) .

Biểu diễn tỉ số diện tích hai tam giác đồng dạng \({S_{\Delta HBC}}\) và \({S_{\Delta HAO}}\)

Ta có: \({S_{BCHO}} = {S_{\Delta HBC}} + {S_{\Delta HOB}}\), biến đổi về \({S_{\Delta AOM}}\), ta tính được \({S_{BCHO}}\).

Lời giải

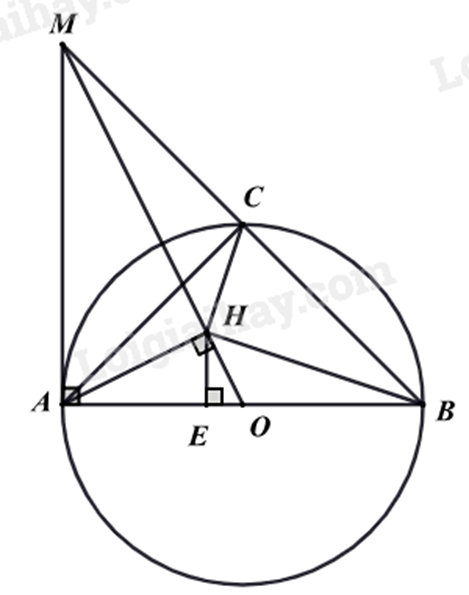
a) Ta có \(\widehat {ACB} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn) nên \(\widehat {ACM} = 90^\circ \)

Xét \(\Delta MAC\) vuông tại C \(\left( {\widehat {ACM} = 90^\circ } \right)\) nên \(\Delta MAC\) nội tiếp đường tròn đường kính AM, suy ra M, A, C cùng thuộc đường tròn đường kính AM.

Xét \(\Delta MAH\)vuông tại H \(\left( {AH \bot OM} \right)\) nên \(\Delta MAH\) nội tiếp đường tròn đường kính AM, suy ra M, A, H cùng thuộc đường tròn đường kính AM.

Vậy A, M, C, H cùng thuộc đường tròn đường kính AM hay tứ giác AMCH nội tiếp.

b) Chứng minh \(M{A^2} = MB.MC\)

Xét \(\Delta MAC\) và \(\Delta MBA\) có:

\(\widehat {AMB}\) chung

\(\widehat {MCA} = \widehat {MAB}\left( { = 90^\circ } \right)\)

Nên \(\Delta MAC\,\backsim \,\Delta MBA\) (g.g)

Suy ra \(\frac{{MA}}{{MB}} = \frac{{MC}}{{MA}}\) hay \(M{A^2} = MB.MC\)

Chứng minh  \(\frac{{MB}}{{MC}} = \frac{{A{B^2}}}{{A{C^2}}}\)

Xét \(\Delta ABM\) có: \(\widehat {MAB} = 90^\circ \) và AB = AM = 2R nên \(\Delta ABM\) vuông cân tại A

Vì \(\widehat {ACM} = 90^\circ \) nên AC là đường cao, do đó AC cũng là đường trung tuyến

Suy ra \(MC = CB = \frac{1}{2}MB\) (C là trung điểm của BM) hay \(\frac{{MB}}{{MC}} = 2\) (1)

và \(AC = CM = CB = \frac{1}{2}MB\) (tính chất đường trung tuyến ứng với cạnh huyền)

Áp dụng định lí Pythagore vào \(\Delta CAB\) vuông cân tại C, ta có:

\(A{B^2} = A{C^2} + C{B^2}\)

\(A{B^2} = 2A{C^2}\) (do AC = CB)

Suy ra \(\frac{{A{B^2}}}{{A{C^2}}} = 2\) (2)

Từ (1) và (2) suy ra \(\frac{{MB}}{{MC}} = \frac{{A{B^2}}}{{A{C^2}}} = 2\)

c) Chứng minh \(HB \bot HC\)

Áp dụng định lí Pythagore vào \(\Delta AOM\) vuông tại A nên \(O{M^2} = A{M^2} + A{O^2}\)

\(OM = \sqrt {A{M^2} + A{O^2}}  = \sqrt {4{R^2} + {R^2}}  = R\sqrt 5 \)

Xét \(\Delta HOA\) và \(\Delta AOM\) có:

\(\widehat {AHO} = \widehat {MAO}\left( { = 90^\circ } \right)\)

\(\widehat {AOH}\) chung

nên \(\Delta \,HOA\backsim \,\Delta AOM\) (g. g)

suy ra \(\frac{{HO}}{{AO}} = \frac{{HA}}{{AM}} = \frac{{OA}}{{OM}} = \frac{R}{{R\sqrt 5 }} = \frac{1}{{\sqrt 5 }}\)

do đó \(HA = \frac{{AM}}{{\sqrt 5 }} = \frac{{2R}}{{\sqrt 5 }}\)

Xét \(\Delta AOM\) và \(\Delta HAM\) có:

\(\widehat {MAO} = \widehat {MHA}\left( { = 90^\circ } \right)\)

\(\widehat {AMH}\) chung

nên \(\Delta \,AOM\backsim \,\Delta HAM\) (g. g)

suy ra \(\frac{{AO}}{{HA}} = \frac{{AM}}{{HM}} = \frac{{OM}}{{AM}} = \frac{{R\sqrt 5 }}{{2R}} = \frac{{\sqrt 5 }}{2}\)

do đó \(HM = \frac{{2AM}}{{\sqrt 5 }} = \frac{{4R}}{{\sqrt 5 }}\)

Vì \(\Delta \,HOA\backsim \,\Delta AOM\) và \(\Delta \,AOM\backsim \,\Delta HAM\) nên \(\Delta \,HOA\backsim \,\Delta HAM\)

Do đó \(\frac{{HO}}{{HA}} = \frac{{OA}}{{AM}} = \frac{{HA}}{{HM}} = \frac{{2R}}{{\sqrt 5 }}:\frac{{4R}}{{\sqrt 5 }} = \frac{1}{2}\) (3)

Mặt khác, \(AC = \frac{1}{2}MB\) (cmt) nên \(\frac{{AC}}{{MB}} = \frac{1}{2}\) (4)

Từ (3) và (4) suy ra: \(\frac{{HA}}{{HM}} = \frac{{AC}}{{MB}}\left( { = \frac{1}{2}} \right)\)

Xét \(\Delta MHB\) và \(\Delta AHC\) có:

\(\widehat {BMH} = \widehat {CAH}\) (cùng chắn cung HC)

\(\frac{{HA}}{{HM}} = \frac{{AC}}{{MB}}\) (cmt)

Nên \(\Delta \,MHB\backsim \,\Delta AHC\) (c.g.c)

suy ra \(\widehat {MHB} = \widehat {AHC}\) (cặp góc tương ứng)

Mà \(\widehat {MHB} = \widehat {MHC} + \widehat {CHB}\); \(\widehat {AHC} = \widehat {MHC} + \widehat {AHM}\)

Suy ra \(\widehat {CHB} = \widehat {AHM} = 90^\circ \)

Vậy \(HB \bot HC\)

Tính diện tích tứ giác \(BCHO\) theo \(R\).

Từ H kẻ \(HE \bot AO\)

Ta có \({S_{\Delta HOA}} = \frac{1}{2}HE.AO\); \({S_{\Delta HOB}} = \frac{1}{2}HE.BO\) (\(AO = BO = R\))

Nên \({S_{\Delta HOA}} = {S_{\Delta HOB}}\)

Vì \(\Delta \,HOA\backsim \,\Delta AOM\) (cmt) nên \(\frac{{{S_{\Delta HOA}}}}{{{S_{\Delta AOM}}}} = {\left( {\frac{{OA}}{{OM}}} \right)^2} = {\left( {\frac{R}{{R\sqrt 5 }}} \right)^2} = \frac{1}{5}\), suy ra \({S_{\Delta HOA}} = \frac{1}{5}{S_{\Delta AOM}}\)

Xét \(\Delta ABC\) có \(\widehat {ACB} = 90^\circ \), AC  = BC nên \(\Delta ABC\) vuông cân tại C. Áp dụng định lí Pythagore, ta có:

\(\begin{array}{l}A{C^2} + B{C^2} = A{B^2}\\2B{C^2} = A{B^2}\\B{C^2} = \frac{{A{B^2}}}{2} = \frac{{4{R^2}}}{2} = 2{R^2}\end{array}\)

Suy ra \(BC = \sqrt {2{R^2}}  = R\sqrt 2 \)

Ta có: \(\widehat {AMH} = \widehat {ACH}\) (hai góc nội tiếp chắn cung AH)

Mà \(\widehat {AMH} = \widehat {HAO}\) (do \(\Delta \,HOA\backsim \,\Delta AOM\))

nên \(\widehat {HCA} = \widehat {HAO}\) hay \(\widehat {HCA} = \widehat {HAB}\)

Mà \(\Delta \,MHB\backsim \,\Delta AHC\) nên \(\widehat {HCA} = \widehat {HBC}\) (hai góc tương ứng)

Suy ra \(\widehat {HAB} = \widehat {HBC}\)

Xét \(\Delta HAO\) và \(\Delta HBC\) có:

\(\widehat {AHO} = \widehat {CHB} = 90^\circ \)

\(\widehat {HAO} = \widehat {HBC}\) (do \(\widehat {HAB} = \widehat {HBC}\))

nên \(\Delta \,HAO\backsim \,\Delta HBC\) (g.g)

suy ra \(\frac{{HA}}{{HB}} = \frac{{HO}}{{HC}} = \frac{{AO}}{{BC}} = \frac{R}{{R\sqrt 2 }} = \frac{1}{{\sqrt 2 }}\)

Do đó \(\frac{{{S_{\Delta HAO}}}}{{{S_{\Delta HBC}}}} = {\left( {\frac{1}{{\sqrt 2 }}} \right)^2} = \frac{1}{2}\), suy ra \({S_{\Delta HBC}} = 2{S_{\Delta HAO}}\)

Ta có: \({S_{BCHO}} = {S_{\Delta HBC}} + {S_{\Delta HOB}}\)

            \({S_{BCHO}} = 2{S_{\Delta HAO}} + {S_{\Delta HOA}}\)

            \({S_{BCHO}} = 3{S_{\Delta HAO}}\)

\({S_{BCHO}} = 3.\frac{1}{5}{S_{\Delta AOM}} = \frac{3}{5}{S_{\Delta AOM}}\)

Do đó

\({S_{BCHO}} = \frac{3}{5}.\frac{1}{2}.AM.OA = \frac{3}{5}.\frac{1}{2}.2R.R = \frac{3}{5}{R^2}\)