Đề tham khảo thi vào 10 môn Toán TP Hồ Chí Minh năm 2025 - Đề số 4

Đề bài

Câu 1 (1,5 điểm): Cho hàm số \((P):y =  - \;{x^2}\)

a) Vẽ đồ thị \((P)\) của hàm số trên.

b) Tìm những điểm N thuộc \((P)\) có hoành độ và tung độ là những số đối nhau.

Câu 2 (1 điểm): Cho phương trình \({x^2} - 4x - 6 = 0\).

a) Chứng minh phương trình trên có hai nghiệm phân biệt \({x_1},{x_2}\).

b) Không giải phương trình, hãy tính giá trị của biểu thức \(A = \frac{{{x_1}{x_2}}}{{4 - {x_1}}} + \frac{{{x_1}{x_2}}}{{4 - {x_2}}}\).

Câu 3 (1,5 điểm): Biểu đồ cột kép bên dưới biểu diễn số học sinh khối 9 của trường THCS A trên địa bàn Thành phố Hồ Chí Minh tham gia các câu lạc bộ do nhà trường tổ chức. Biết rằng mỗi bạn chỉ tham gia đúng một câu lạc bộ.

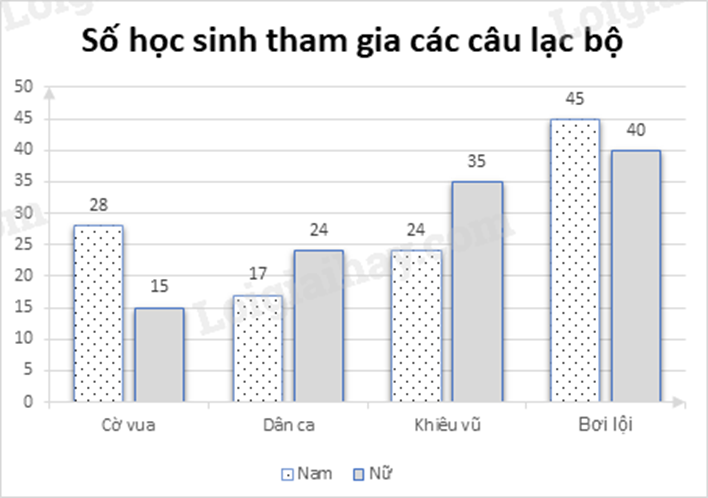
a) Câu lạc bộ nào có sự chênh lệch nhiều nhất giữa số nam sinh và nữ sinh?

b) Chọn ngẫu nhiên một học sinh khối 9, tính xác suất của các biến cố sau:

A: “Học sinh được chọn là nữ”.

B: “Học sinh được chọn không tham gia câu lạc bộ bơi lội và câu lạc bộ khiêu vũ”.

Câu 4 (1 điểm): Một cái sân hình chữ nhật có độ dài của một cạnh như hình vẽ. Ở góc sân, người ta làm một cái bồn hoa hình tròn có bán kính \(x\) mét (\(x > 0\)). Biết vòng tròn tiếp xúc với 2 cạnh của hình chữ nhật và khoảng cách từ cạnh (chiều dài) của hình chữ nhật đến đường tròn là 2 mét (xem hình minh họa). (lấy \(\pi  = 3,14\)).

a) Viết biểu thức biểu thị diện tích đất còn lại sau khi đã xây bồn hoa.

b) Hãy tính bán kính của bồn hoa hình tròn biết diện tích đất còn lại sau khi xây bồn hoa là \(54,71{m^2}\).

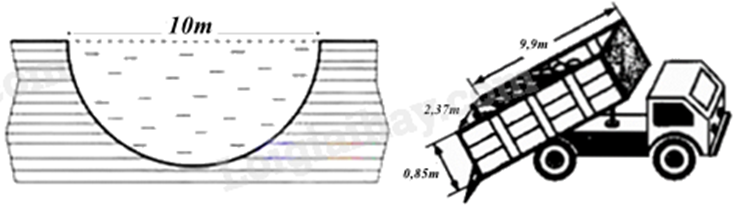
Câu 5 (1 điểm): Để phòng tránh trẻ em bị đuối nước, người ta quyết định dùng đất để lấp một cái ao dạng nửa hình cầu, mặt ao hình tròn có đường kính 10m.

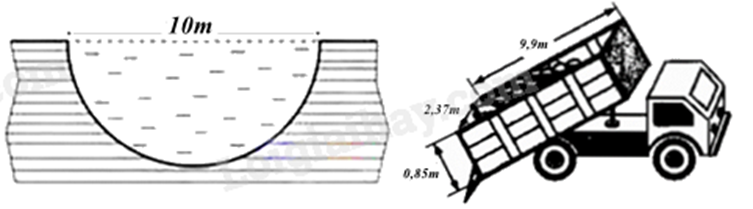
a) Tính thể tích nước trong ao theo \({m^3}\). Giả sử mực nước trong ao bằng với mặt đất xung quanh và các sinh vật, vật thể trong ao có thể tích không đáng kể.

b) Người ta thuê những xe tải có thùng xe dạng hình hộp chữ nhật, lòng trong thùng dài 9,9 mét, rộng 2,37 mét và cao 0,85 mét. Nhưng con đường từ nơi cung cấp đất đến ao bị giới hạn trọng tải của phương tiện tham gia giao thông nên xe chỉ chở được 85% thể tích của lòng trong thùng xe. Hỏi cần thuê ít nhất bao nhiêu xe để lấp đầy cái ao? (Đất chở trên xe gần được nén chặt và gần như không có khoảng trống trong khối đất)

(Cho biết công thức tính thể tích hình cầu là \(V = \frac{4}{3}\pi {R^3}\), trong đó R là bán kính hình cầu. Kết quả làm tròn đến hàng phần mười)

Câu 6 (1 điểm): Một ô tô dự định đi từ A đến B trong một thời gian nhất định. Nếu xe chạy mỗi giờ nhanh hơn 12,5km/h thì đến sớm hơn dự định 2 giờ, còn xe chạy chậm đi 10km/h thì đến nơi chậm mất 2,5 giờ.

a) Tính vận tốc của xe lúc đầu, thời gian dự định và chiều dài quãng đường AB.

b) Trên quãng đường cao tốc CD = 150km có vận tốc giới hạn từ 50km/h đến 120km/h thì một ô tô đi hết cao tốc trong khoảng thời gian nào?

Câu 7 (3 điểm): Cho \(\Delta ABC\) nhọn \((AB < AC)\). Đường tròn \(\left( O \right)\) đường kính \(BC\) cắt \(AB,AC\) lần lượt tại \(E,D\) (\(E\) không trùng \(B\), \(D\) không trùng \(C\)). \(BD\) cắt \(CE\) tại \(H\), \(AH\) cắt \(BC\) tại \(F\).

a) Chứng minh \(AF \bot BC\) và tứ giác \(BEHF\) nội tiếp.

b) Chứng minh \(FA\) là tia phân giác của \(\widehat {EFD}\) và \(FE \cdot FD = FH \cdot FA\).

c) Trên tia đối của tia \(FE\) lấy điểm \(K\) sao cho \(FK = FD\). Với \(BC = 11cm\), \(FE = 4cm\), \(FK = 6cm\) \((FB < FC)\), tính số đo góc \(\widehat {BKC}\) và độ dài FO.

-------- HẾT --------

Lời giải

Câu 1 (1,5 điểm): Cho hàm số \((P):y =  - \;{x^2}\)

a) Vẽ đồ thị \((P)\) của hàm số trên.

b) Tìm những điểm N thuộc \((P)\) có hoành độ và tung độ là những số đối nhau.

Phương pháp

a) Lập bảng giá trị, vẽ đồ thị hàm số trên hệ trục tọa độ.

b) Điểm có hoành độ và tung độ là những số đối nhau có dạng \(N\left( {{x_0}; - {x_0}} \right)\).

Vì \(N \in (P)\) nên \(N\left( {{x_0}; - x_0^2} \right)\).

Do đó \( - {x_0} =  - x_0^2\)

Giải phương trình để tìm N thoả mãn.

Lời giải

Ta có bảng giá trị sau:

Đồ thị hàm số là đường cong parabol đi qua các điểm \(O\,\left( {0;0} \right);A\left( { - 2; - 4} \right);\,\,B\left( { - 1; - 1} \right);C\left( {1; - 1} \right);\,\,D\left( {2; - 4} \right)\)

Hệ số \(a =  - 1 < 0\) nên parabol có bề cong hướng xuống. Đồ thị hàm số nhận Oy làm trục đối xứng.

Ta vẽ được đồ thị hàm số \(y =  - {x^2}\) như sau:

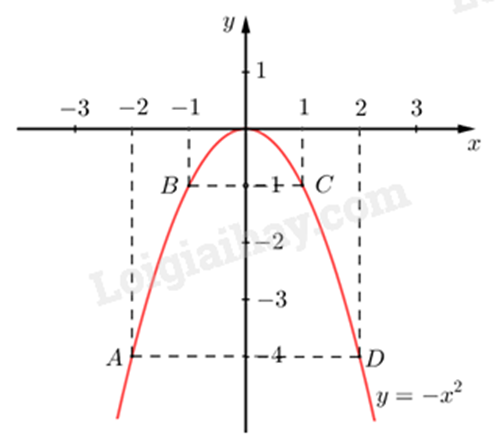
b) Điểm có hoành độ và tung độ là những số đối nhau có dạng \(N\left( {{x_0}; - {x_0}} \right)\).

Vì \(N \in (P)\) nên \(N\left( {{x_0}; - x_0^2} \right)\).

Do đó \( - {x_0} =  - x_0^2\)

\(x_0^2 - {x_0} = 0\)

\({x_0}\left( {{x_0} - 1} \right) = 0\)

suy ra \({x_0} = 0\) hoặc \({x_0} - 1 = 0\)

 \({x_0} = 0\) hoặc \({x_0} = 1\)

Khi đó \({y_0} = 0\) hoặc \({y_0} =  - 1\)

Vậy điểm \(N\) cần tìm là \(N\left( {0;0} \right)\) và \(N\left( {1; - 1} \right)\).

Câu 2 (1 điểm): Cho phương trình \({x^2} - 4x - 6 = 0\).

a) Chứng minh phương trình trên có hai nghiệm phân biệt \({x_1},{x_2}\).

b) Không giải phương trình, hãy tính giá trị của biểu thức \(A = \frac{{{x_1}{x_2}}}{{4 - {x_1}}} + \frac{{{x_1}{x_2}}}{{4 - {x_2}}}\).

Phương pháp

a) Kiểm tra nghiệm của phương trình theo \(a.c\).

b) Áp dụng định lí Viète và biến đổi.

Định lí Viète: \({x_1} + {x_2} = \frac{{ - b}}{a};{x_1}{x_2} = \frac{c}{a}\)

Lời giải

a) Vì \(a.c = 1.\left( { - 6} \right) =  - 6 < 0\) nên phương trình có hai nghiệm phân biệt \({x_1},{x_2}\).

b) Theo định lí Viète, ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = \frac{{ - b}}{a} = \frac{{ - ( - 4)}}{1} = 4\\{x_1}{x_2} = \frac{c}{a} = \frac{{ - 6}}{1} =  - 6\end{array} \right.\)

Ta có: \(A = \frac{{{x_1}{x_2}}}{{4 - {x_1}}} + \frac{{{x_1}{x_2}}}{{4 - {x_2}}}\)

\( = \frac{{{x_1}{x_2}(4 - {x_2}) + {x_1}{x_2}(4 - {x_1})}}{{(4 - {x_1})(4 - {x_2})}}\)

\( = \frac{{4{x_1}{x_2} - {x_1}x_2^2 + 4{x_1}{x_2} - x_1^2{x_2}}}{{16 - 4{x_1} - 4{x_2} + {x_1}{x_2}}}\)

\( = \frac{{8{x_1}{x_2} - {x_1}{x_2}\left( {{x_1} + {x_2}} \right)}}{{16 - 4({x_1} + {x_2}) + {x_1}{x_2}}}\)

\( = \frac{{{x_1}{x_2}\left[ {8 - \left( {{x_1} + {x_2}} \right)} \right]}}{{16 - 4({x_1} + {x_2}) + {x_1}{x_2}}}\)

\( = \frac{{ - 6.\left( {8 - 4} \right)}}{{16 - 4.4 - 6}}\)

\( = \frac{{ - 24}}{{ - 6}}\)

\( = 4\).

Vậy \(A = 4\).

Câu 3 (1,5 điểm): Biểu đồ cột kép bên dưới biểu diễn số học sinh khối 9 của trường THCS A trên địa bàn Thành phố Hồ Chí Minh tham gia các câu lạc bộ do nhà trường tổ chức. Biết rằng mỗi bạn chỉ tham gia đúng một câu lạc bộ.

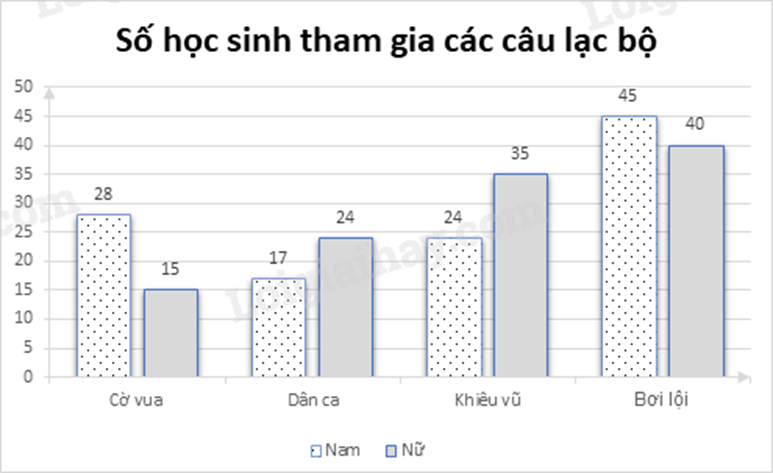
a) Câu lạc bộ nào có sự chênh lệch nhiều nhất giữa số nam sinh và nữ sinh?

b) Chọn ngẫu nhiên một học sinh khối 9, tính xác suất của các biến cố sau:

A: “Học sinh được chọn là nữ”.

B: “Học sinh được chọn không tham gia câu lạc bộ bơi lội và câu lạc bộ khiêu vũ”.

Phương pháp

a) Từ các cột số liệu, tính sự chênh lệch giữa số nam sinh và nữ sinh bằng số lớn – số bé.

Giá trị nào lớn nhất thì sự chênh lệch giữa số nam sinh và nữ sinh là lớn nhất.

b) Xác định tổng số học sinh tham gia câu lạc bộ của khối 9.

Xác định số kết quả thuận lợi cho biến cố A, B.

Xác suất của biến cố bằng tỉ số giữa số kết quả thuận lợi và tổng số kết quả có thể (tổng số học sinh).

Lời giải

a) Từ biểu đồ, ta có sự chênh lệch giữa số nam sinh và nữ sinh như sau:

Câu lạc bộ cờ vua: 28 – 15 = 13

Câu lạc bộ dân ca: 24 – 17 = 7

Câu lạc bộ khiêu vũ: 35 – 24 = 11

Câu lạc bộ bơi lội: 45 – 40 = 5

Vì 13 > 11 > 7 > 5 nên câu lạc bộ cờ vua có sự chênh lệch nhiều nhất giữa số nam sinh và nữ sinh.

b) Tổng số học sinh tham gia câu lạc bộ của khối 9 là:

28 + 15 + 17 + 24 + 24 + 35 + 45 + 40 = 228 (học sinh)

Số kết quả thuận lợi của biến cố A: “Học sinh được chọn là nữ” là:

15 + 24 + 35 + 40 = 114.

Vậy xác suất của các biến cố A: “Học sinh được chọn là nữ” là: \(\frac{{114}}{{228}} = \frac{1}{2}\).

Số kết quả thuận lợi của biến cố B: “Học sinh được chọn không tham gia câu lạc bộ bơi lội và câu lạc bộ khiêu vũ” là:

28 + 15 + 17 + 24 = 84

Vậy xác suất của các biến cố B: “Học sinh được chọn không tham gia câu lạc bộ bơi lội và câu lạc bộ khiêu vũ” là: \(\frac{{84}}{{228}} = \frac{7}{{19}}\).

Câu 4 (1 điểm): Một cái sân hình chữ nhật có độ dài của một cạnh như hình vẽ. Ở góc sân, người ta làm một cái bồn hoa hình tròn có bán kính \(x\) mét (\(x > 0\)). Biết vòng tròn tiếp xúc với 2 cạnh của hình chữ nhật và khoảng cách từ cạnh (chiều dài) của hình chữ nhật đến đường tròn là 2 mét (xem hình minh họa). (lấy \(\pi  = 3,14\))

a) Viết biểu thức biểu thị diện tích đất còn lại sau khi đã xây bồn hoa.

b) Hãy tính bán kính của bồn hoa hình tròn biết diện tích đất còn lại sau khi xây bồn hoa là \(54,71{m^2}\).

Phương pháp

a) Biểu diễn chiều rộng của sân theo \(x\).

Khi đó tính diện tích của sân: S = CD.CR.

Diện tích của bồn hoa: \(S = \pi {r^2}\).

Diện tích còn lại = diện tích của sân – diện tích của bồn hoa.

b) Vì diện tích đất còn lại sau khi xây bồn hoa là \(54,71{m^2}\) nên ta viết được phương trình.

Từ đó giải phương trình để tìm \(x\).

Lời giải

a) Chiều rộng của sân là: \(2x + 2\left( m \right)\)

Khi đó diện tích của sân là: \(\left( {1,57x + 10} \right)\left( {2x + 2} \right) = 3,14{x^2} + 23,14x + 20\left( {{m^2}} \right)\)

Diện tích của bồn hoa là: \({x^2}\pi  = 3,14{x^2}\left( {{m^2}} \right)\)

Diện tích đất còn lại sau khi đã xây bồn hoa là: \(3,14{x^2} + 23,14x + 20 - 3,14{x^2} = 23,14x + 20\left( {{m^2}} \right)\)

b) Vì diện tích đất còn lại sau khi xây bồn hoa là \(54,71{m^2}\) nên ta có phương trình:

\(23,14x + 20 = 54,71\)

\(23,14x = 34,71\)

\(x = 1,5\)

Vậy bán kính của bồn hoa là 1,5m.

Câu 5 (1 điểm): Để phòng tránh trẻ em bị đuối nước, người ta quyết định dùng đất để lấp một cái ao dạng nửa hình cầu, mặt ao hình tròn có đường kính 10m.

a) Tính thể tích nước trong ao theo \({m^3}\). Giả sử mực nước trong ao bằng với mặt đất xung quanh và các sinh vật, vật thể trong ao có thể tích không đáng kể.

b) Người ta thuê những xe tải có thùng xe dạng hình hộp chữ nhật, lòng trong thùng dài 9,9 mét, rộng 2,37 mét và cao 0,85 mét. Nhưng con đường từ nơi cung cấp đất đến ao bị giới hạn trọng tải của phương tiện tham gia giao thông nên xe chỉ chở được 85% thể tích của lòng trong thùng xe. Hỏi cần thuê ít nhất bao nhiêu xe để lấp đầy cái ao? (Đất chở trên xe gần được nén chặt và gần như không có khoảng trống trong khối đất)

(Cho biết công thức tính thể tích hình cầu là \(V = \frac{4}{3}\pi {R^3}\), trong đó R là bán kính hình cầu. Kết quả làm tròn đến hàng phần mười)

Phương pháp

a) Thể tích nước trong ao bằng thể tích của nửa hình cầu: \({V_{nc}} = \frac{1}{2}.\)V_{hình cầu}.

b) Sử dụng công thức tính thể tích hình hộp chữ nhật để tính thể tích lòng trong thùng: \({V_{xe}} = d.r.c\)

Tính thể tích đất mỗi xe chở được = \(85\% .{V_{xe}}\).

Tính tỉ số giữa thể tích ao với thể tích đất mỗi xe chở được suy ra số xe cần thuê ít nhất.

Lời giải

a) Thể tích nước trong ao chính là thể tích của nửa hình cầu đường kính 10km.

Bán kính của ao là: 10 : 2 = 5 (m)

Thể tích nước trong ao là: \({V_{nc}} = \frac{1}{2}.\frac{4}{3}.\pi {.5^3} \approx 261,8\left( {{m^3}} \right)\)

Vậy thể tích nước trong ao khoảng \(261,8{m^2}\).

b) Thể tích của lòng trong thùng xe tải là: \({V_{xe}} = 9,9.2,37.0,85 \approx 19,9\left( {{m^3}} \right)\)

Thể tích đất xe chở được là: \(85\% .19,9 \approx 16,9\left( {{m^3}} \right)\)

Vì người ta dùng đất để lấp đầy ao nên lượng đất dùng để lấp đầy ao bằng thể tích nước trong ao.

Ta có: \(\frac{{{V_{nc}}}}{{{V_{xe}}}} = \frac{{261,8}}{{16,9}} \approx 15,5\)

Vậy cần thuê ít nhất 16 chiếc xe để lấp đầy cái ao.

Câu 6 (1 điểm): Một ô tô dự định đi từ A đến B trong một thời gian nhất định. Nếu xe chạy mỗi giờ nhanh hơn 12,5km/h thì đến sớm hơn dự định 2 giờ, còn xe chạy chậm đi 10km/h thì đến nơi chậm mất 2,5 giờ.

a) Tính vận tốc của xe lúc đầu, thời gian dự định và chiều dài quãng đường AB.

b) Trên quãng đường cao tốc CD = 150km có vận tốc giới hạn từ 50km/h đến 120km/h thì một ô tô đi hết cao tốc trong khoảng thời gian nào?

Phương pháp

a) Gọi \(x\) (km/h) là vận tốc xe ô tô dự định (\(x > 10\))

Gọi \(y\) (h) là thời gian dự định của ô tô (\(y > 3\))

Biểu diễn quãng đường AB theo \(x,y\).

Lập phương trình biểu diễn quãng đường đi được nếu vận tốc tăng 12,5km/h thì xe đến sớm hơn dự định 2 giờ.

Lập phương trình biểu diễn quãng đường đi được nếu vận tốc giảm 10km/h thì xe đến nơi chậm 2,5 giờ.

Từ đó lập hệ phương trình.

Giải hệ phương trình để tìm \(x,y\).

b) Gọi thời gian đi hết quãng đường của ô tô là \(a\left( h \right)\).

Vì vận tốc của ô tô trong khoảng từ 50km/h đến 120km/h nên ta có bất phương trình \(50 \le \frac{{150}}{a} \le 120\)

Giải các bất phương trình để tìm a.

Lời giải

a) Gọi \(x\) (km/h) là vận tốc xe ô tô dự định (\(x > 10\))

Gọi \(y\) (h) là thời gian dự định của ô tô (\(y > 3\))

Khi đó quãng đường AB là: \(xy\) (km).

Nếu vận tốc tăng 12,5km/h thì xe đến sớm hơn dự định 2 giờ nên ta có phương trình:

\(\begin{array}{l}\left( {x + 12,5} \right)\left( {y - 2} \right) = xy\\xy - 2x + 12,5y - 25 = xy\\ - 2x + 12,5y = 25\left( 1 \right)\end{array}\)

Nếu vận tốc giảm 10km/h thì đến nơi chậm 2,5 giờ nên ta có phương trình:

\(\begin{array}{l}\left( {x - 10} \right)\left( {y + 2,5} \right) = xy\\xy + 2,5x - 10y - 25 = xy\\2,5x - 10y = 25\left( 2 \right)\end{array}\)

Từ (1) và (2) ta có hệ phương trình: \(\left\{ \begin{array}{l} - 2x + 12,5y = 25\\2,5x - 10y = 25\end{array} \right.\).

Giải hệ phương trình ta được: \(\left\{ \begin{array}{l}x = 50\\y = 10\end{array} \right.\)

Vậy vận tốc dự định của xe là 50km/h, thời gian dự định là 10 giờ và quãng đường AB là \(50.10 = 500km\).

b) Gọi thời gian đi hết quãng đường của ô tô là \(a\left( h \right)\).

Vì vận tốc của ô tô trong khoảng từ 50km/h đến 120km/h nên ta có bất phương trình:

\(50 \le \frac{{150}}{a} \le 120\)

* Giải bất phương trình \(50 \le \frac{{150}}{a}\) ta được \(a \le \frac{{150}}{{50}} = 3\)

* Giải bất phương trình \(\frac{{150}}{a} \le 120\) ta được \(a \ge \frac{{150}}{{120}} = 1,25\)

Suy ra \(1,25 \le a \le 3\).

Vậy xe đi hết cao tốc trong khoảng thời gian từ 1,25 giờ (= 1 giờ 15 phút) đến 3 giờ.

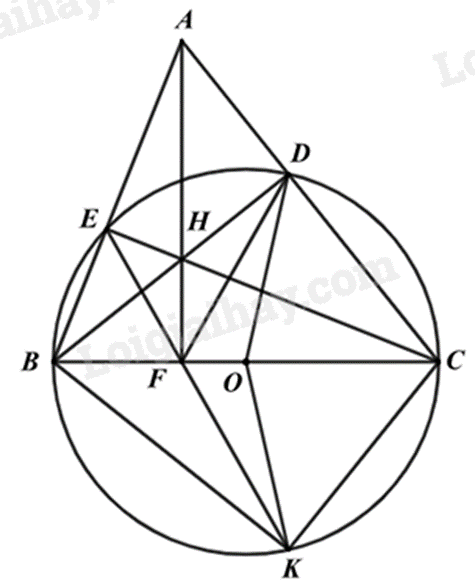
Câu 7 (3 điểm): Cho \(\Delta ABC\) nhọn \((AB < AC)\). Đường tròn \(\left( O \right)\) đường kính \(BC\) cắt \(AB,AC\) lần lượt tại \(E,D\) (\(E\) không trùng \(B\), \(D\) không trùng \(C\)). \(BD\) cắt \(CE\) tại \(H\), \(AH\) cắt \(BC\) tại \(F\).

a) Chứng minh \(AF \bot BC\) và tứ giác \(BEHF\) nội tiếp.

b) Chứng minh \(FA\) là tia phân giác của \(\widehat {EFD}\) và \(FE \cdot FD = FH \cdot FA\).

c) Trên tia đối của tia \(FE\) lấy điểm \(K\) sao cho \(FK = FD\). Với \(BC = 11cm\), \(FE = 4cm\), \(FK = 6cm\) \((FB < FC)\), tính số đo góc \(\widehat {BKC}\) và độ dài FO.

Phương pháp

a) Chứng minh \(AF \bot BC\)

Chứng minh H là trực tâm của tam giác ABC và \(AH\) cắt \(BC\) tại \(F\) nên AF là đường cao, suy ra \(AF \bot BC\).

Chứng minh tứ giác \(BEHF\) nội tiếp.

Chứng minh tam giác vuông BHE và BHF cùng nội tiếp đường tròn đường kính BH nên BEHF nội tiếp.

b) Chứng minh \(FA\) là tia phân giác của \(\widehat {EFD}\)

Vì BEHF là tứ giác nội tiếp nên \(\widehat {EFH} = \widehat {EBH}\)

Chứng minh tứ giác \(CDHF\) là tứ giác nội tiếp nên \(\widehat {HFD} = \widehat {HCD}\)

Mà \(\widehat {EBH} = \widehat {HCD}\)

suy ra \(\widehat {EFH} = \widehat {HFD}\), suy ra \(FA\) là tia phân giác của \(\widehat {EFD}\).

Chứng minh \(FE \cdot FD = FH \cdot FA\)

Chứng minh tứ giác \(ABFD\) là tứ giác nội tiếp nên \(\widehat {BAF} = \widehat {BDF}\)

Chứng minh $\Delta FAE\backsim \Delta FDH$ (g.g)

Do đó \(\frac{{FE}}{{FA}} = \frac{{FH}}{{FD}}\), suy ra \(FE \cdot FD = FH \cdot FA\).

c) Tính \(\widehat {BKC}\)

Sử dụng tính chất hai góc đối đỉnh và góc nội tiếp cùng chắn một cung suy ra \(\widehat {DFO} = \widehat {KFO}\)

Chứng minh \(\Delta FDO = \Delta FKO\) suy ra \(OK = OD\) nên \(K \in \left( O \right)\), suy ra \(\widehat {BKC} = 90^\circ \).

Tính FO

Đặt \(FB = x\left( {x < r} \right)\).

Chứng minh $\Delta BEF\backsim \Delta KCF$ suy ra \(FE \cdot FK = FB \cdot FC\)

Từ đó viết phương trình theo \(x\).

Giải phương trình để tìm FB. Khi đó ta tính được FO = BO – FB.

Lời giải

a) Chứng minh \(AF \bot BC\)

Ta có: \(\widehat {BEC} = \widehat {BDC} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn) nên \(CE \bot AB,BD \bot AC\).

Do đó \(BD,CE\) là hai đường cao của tam giác ABC.

Mà BD và CE cắt nhau tại \(H\) nên H là trực tâm của tam giác ABC.

Do đó \(AF\) là đường cao của tam giác ABC (vì \(AH\) cắt \(BC\) tại \(F\)) nên \(AF \bot BC\).

Chứng minh tứ giác \(BEHF\) nội tiếp

Vì \(\Delta BHE\) vuông tại E nên \(\Delta BHE\) nội tiếp đường tròn đường kính BH.

Vì \(\Delta BHF\) vuông tại F nên \(\Delta BHF\) nội tiếp đường tròn đường kính BH.

Do đó bốn điểm B, E, H, F thuộc đường tròn đường kính BH hay tứ giác \(BEHF\) là tứ giác nội tiếp.

b) Chứng minh \(FA\) là tia phân giác của \(\widehat {EFD}\)

Vì BEHF là tứ giác nội tiếp nên \(\widehat {EFH} = \widehat {EBH}\) (hai góc nội tiếp cùng chắn cung EH). (1)

Vì \(\Delta CDH\) vuông tại D nên \(\Delta CDH\) nội tiếp đường tròn đường kính CH.

Vì \(\Delta CHF\) vuông tại F nên \(\Delta CHF\) nội tiếp đường tròn đường kính CH.

Do đó bốn điểm C, D, H, F thuộc đường tròn đường kính CH hay tứ giác \(CDHF\) là tứ giác nội tiếp.

Do đó \(\widehat {HFD} = \widehat {HCD}\) (hai góc nội tiếp cùng chắn cung HD). (2)

Mà \(\widehat {EBH} = \widehat {HCD}\) (hai góc nội tiếp cùng chắn cung ED) (3)

Từ (1), (2) và (3) suy ra \(\widehat {EFH} = \widehat {HFD}\), suy ra \(FA\) là tia phân giác của \(\widehat {EFD}\).

Chứng minh \(FE \cdot FD = FH \cdot FA\)

Vì \(\Delta ABD\) vuông tại D nên \(\Delta ABD\) nội tiếp đường tròn đường kính AB.

Vì \(\Delta ABF\) vuông tại F nên \(\Delta ABF\) nội tiếp đường tròn đường kính AB.

Do đó bốn điểm A, B, F, D thuộc đường tròn đường kính AB hay tứ giác \(ABFD\) là tứ giác nội tiếp.

Suy ra \(\widehat {BAF} = \widehat {BDF}\) (hai góc nội tiếp cùng chắn cung BF)

Xét \(\Delta FAE\) và \(\Delta FDH\) có:

\(\widehat {EFH} = \widehat {HFD}\) (cmt)

\(\widehat {BAF} = \widehat {BDF}\) (cmt)

Suy ra $\Delta FAE\backsim \Delta FDH$ (g.g)

Do đó \(\frac{{FE}}{{FA}} = \frac{{FH}}{{FD}}\), suy ra \(FE \cdot FD = FH \cdot FA\).

c) Tính \(\widehat {BKC}\)

Ta có: \(\widehat {BHE} = \widehat {DHC}\) (hai góc đối đỉnh)

\(\widehat {BFE} = \widehat {KFO}\) (hai góc đối đỉnh)

Mà \(\widehat {BFE} = \widehat {BHE}\) (hai góc nội tiếp cùng chắn cung BE).

\(\widehat {DHC} = \widehat {DFO}\) (hai góc nội tiếp cùng chắn cung DC)

Suy ra \(\widehat {DFO} = \widehat {KFO}\).

Xét \(\Delta FDO\) và \(\Delta FKO\) có:

\(DF = FK\) (gt)

\(\widehat {DFO} = \widehat {KFO}\) (cmt)

OF chung

nên \(\Delta FDO = \Delta FKO\) (c.g.c)

Suy ra \(OK = OD\) = bán kính nên \(K \in \left( O \right)\), suy ra \(\widehat {BKC} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn).

Tính độ dài FO

Ta có BC = 11cm nên BO = OC = \(\frac{{11}}{2} = 5,5\)cm.

Đặt \(FB = x\left( {x < 5,5} \right)\), suy ra \(FC = 11 - x\).

Xét \(\Delta BEF\) và \(\Delta KCF\) có:

\(\widehat {EBF} = \widehat {FKC}\) (hai góc nội tiếp cùng chắn cung EC)

\(\widehat {BFE} = \widehat {KFC}\) (hai góc đối đỉnh)

nên suy ra \(\frac{{FE}}{{FB}} = \frac{{FC}}{{FK}}\), do đó \(FE \cdot FK = FB \cdot FC\)

Thay số, ta được:

\(\begin{array}{l}4 \cdot 6 = x \cdot \left( {11 - x} \right)\\{x^2} - 11x + 24 = 0\end{array}\)

Giải phương trình ta được \(x = 3\) (TM) hoặc \(x = 8\) (KTM)

suy ra \(FB = 3cm\).

Do đó \(FO = 5,5 - 3 = 2,5\left( {cm} \right)\).