Đề thi vào 10 môn Toán Hà Nội năm 2025

Đề bài

Câu I (1,5 điểm)

1) Kết quả khảo sát 300 học sinh lớp 9 về thời gian tự học của mỗi bạn trong một tuần (đơn vị: giờ) được cho trong bảng tần số ghép nhóm sau đây:

Xác định tần số và tần số tương đối của nhóm [12;16).

2) Một hộp có 8 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1,2,3,4,5,6,7,8; hai thẻ khác nhau được ghi hai số khác nhau. Rút ngẫu nhiên một thẻ trong hộp. Tính xác suất của biến cố A: “Số ghi trên thẻ rút được là một số chia hết cho 3".

Câu II (1,5 điểm)

Cho hai biểu thức \(A = \frac{{\sqrt x  + 2}}{{\sqrt x  - 2}}\) và \(B = \frac{{x + \sqrt x  - 4}}{{x - 2\sqrt x }} - \frac{1}{{\sqrt x  - 2}}\) với \(x > 0,x \ne 4\).

1) Tính giá trị của biểu thức A khi \(x = 9\).

2) Chứng minh \(B = \frac{{\sqrt x  + 2}}{{\sqrt x }}\).

3) Tìm số nguyên dương x lớn nhất để \(\frac{A}{B} < \frac{1}{2}\).

Câu III (2,5 điểm)

1) Một ô tô đi từ Hà Nội đến Hải Phòng với vận tốc trung bình 60 km/h. Khi từ Hải Phòng về Hà Nội trên cùng quãng đường đó, do điều kiện thời tiết xấu nên ô tô đi với vận tốc trung bình 40 km/h. Biết thời gian ô tô đi từ Hà Nội đến Hải Phòng ít hơn thời gian ô tô đi từ Hải Phòng về Hà Nội là 1 giờ, tính độ dài quãng đường ô tô đã đi từ Hà Nội đến Hải Phòng.

2) Để chuẩn bị cho năm học mới, bạn Quốc đến cửa hàng mua một chiếc ba lô và một chiếc máy tính cầm tay với tổng giá tiền niêm yết là 885 nghìn đồng. Hiện tại, cửa hàng đó đang triển khai chương trình giảm giá cho học sinh, sinh viên nên giá tiền của một chiếc ba lô giảm 20% và giá tiền của một chiếc máy tính cầm tay giảm 25% so với giá tiền niêm yết. Vì vậy, bạn Quốc chỉ phải trả 682 nghìn đồng khi mua hai sản phẩm này. Hỏi giá tiền niêm yết của một chiếc ba lô và giá tiền niêm yết của một chiếc máy tính cầm tay là bao nhiêu?

3) Biết phương trình bậc hai \({x^2} + 8x - 6 = 0\) có hai nghiệm \({x_1}\) và \({x_2}\), tìm tất cả giá trị của m thỏa mãn \(\frac{{70 - mx_1^2}}{{{x_2}}} = {x_1} + m{x_2}\).

Câu IV (4,0 điểm)

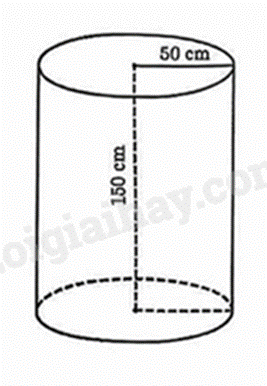
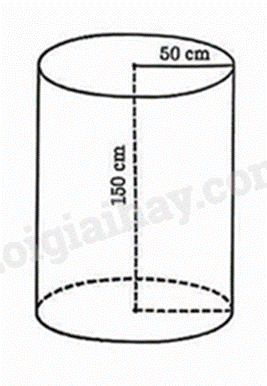
1) Gia đình bạn Khánh đang sử dụng một thùng đựng nước dạng hình trụ với bán kính đáy bằng 50 cm và chiều cao bằng 150 cm. Thùng đựng nước được đặt thẳng đứng trên mặt sàn như hình minh họa bên. (Lấy \(\pi  \approx 3,14\) và coi chiều dày của thùng không đáng kể).

a) Tính diện tích xung quanh của thùng đựng nước.

b) Sau một thời gian gia đình bạn Khánh sử dụng nước trong thùng thì mực nước còn lại đã thấp hơn 40 cm sơ với mực nước ban đầu. Tính thể tích nước trong thùng mà gia đình bạn Khánh đã sử dụng trong khoảng thời gian đó.

2) Cho tam giác ABC có ba góc nhọn (AB < AC), nội tiếp đường tròn (O). Đường cao AD của tam giác ABC cắt đường tròn (O) tại điểm E (E khác A). Gọi K là chân đường vuông góc kẻ từ điểm E đến đường thẳng AB.

a) Chứng minh bốn điểm E, D, B, K cùng thuộc một đường tròn.

b) Đường thẳng AO cắt đường thẳng BC tại điểm S. Chứng minh EA là tia phân giác của góc CEK và AB. AC = AE. AS.

c) Gọi H là trực tâm của tam giác ABC và I là trung điểm của đoạn thẳng AB. Chứng minh đường thẳng SI vuông góc với đường thẳng HK.

Câu V (0,5 điểm)

Một công ty kinh doanh trong lĩnh vực vận tải đang vận hành một đội gồm 35 xe chở hàng cùng loại, với lợi nhuận trung bình của mỗi xe là 1 triệu đồng một ngày. Để mở rộng mô hình kinh doanh, công ty dự định bổ sung một số xe chở hàng cùng loại với xe đang vận hành. Công ty đã tiến hành khảo sát và phân tích thị trường, kết quả cho thấy: cứ bổ sung một xe chở hàng cùng loại vào hoạt động thì lợi nhuận trung bình của mỗi xe trong cả đội lại giảm đi 20 nghìn đồng một ngày. Hỏi công ty nên bổ sung bao nhiêu xe chở hàng cùng loại để lợi nhuận trung bình mỗi ngày của đội xe là lớn nhất?

Lời giải

Câu I (1,5 điểm)

1) Kết quả khảo sát 300 học sinh lớp 9 về thời gian tự học của mỗi bạn trong một tuần (đơn vị: giờ) được cho trong bảng tần số ghép nhóm sau đây:

Xác định tần số và tần số tương đối của nhóm [12;16).

2) Một hộp có 8 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1,2,3,4,5,6,7,8; hai thẻ khác nhau được ghi hai số khác nhau. Rút ngẫu nhiên một thẻ trong hộp. Tính xác suất của biến cố A: “Số ghi trên thẻ rút được là một số chia hết cho 3".

Phương pháp:

1) Quan sát bảng tần số ghép nhóm để xác định tần số (số học sinh) và tính tần số tương đối của nhóm: \(f = \frac{n}{N}.100\% \) với n là tần số của nhóm, N là cỡ mẫu.

2) Xác định số phần tử của không gian mẫu (\(n\left( \Omega  \right)\))

Xác định số kết quả thuận lợi cho biến cố A (\(n\left( A \right)\)).

Xác suất của biến cố là: \(\frac{{n\left( A \right)}}{{n\left( \Omega  \right)}}\).

Lời giải:

1) Tần số tương đối ghép nhóm [12;16) là 75

Tần số tương đối của nhóm [12;16) là \(\frac{{75}}{{300}} \cdot 100{\rm{\% }} = 25{\rm{\% }}\)

2) Xét phép thử: “Rút ngẫu nhiên 1 thẻ trong hộp”

Do 8 chiếc thẻ cùng loại, rút ngẫu nhiên một thẻ trong hộp nên các kết quả xảy ra là đồng khả năng.

Không gian mẫu của phép thử là:

\(\Omega  = \left\{ {1;2;3;4;5;6;7;8} \right\}\)

Suy ra \(n\left( \Omega  \right) = 8\).

Xét biến cố A: “Số ghi trên thẻ rút được là 1 số chia hết cho 3”.

Các kết quả thuận lợi của biến cố A là: 3; 6.

Suy ra \(n\left( A \right) = 2\).

Xác suất của biến cố A là \(P\left( A \right) = \frac{2}{8} = \frac{1}{4}\)

Câu II (1,5 điểm)

Cho hai biểu thức \(A = \frac{{\sqrt x  + 2}}{{\sqrt x  - 2}}\) và \(B = \frac{{x + \sqrt x  - 4}}{{x - 2\sqrt x }} - \frac{1}{{\sqrt x  - 2}}\) với \(x > 0,x \ne 4\).

1) Tính giá trị của biểu thức A khi \(x = 9\).

2) Chứng minh \(B = \frac{{\sqrt x  + 2}}{{\sqrt x }}\).

3) Tìm số nguyên dương x lớn nhất để \(\frac{A}{B} < \frac{1}{2}\).

Phương pháp:

1) Kiểm tra xem \(x = 9\) có thoả mãn điều kiện xác định hay không.

Nếu có, thay \(x = 9\) vào biểu thức để tính.

2) Sử dụng các phép biến đổi với căn thức bậc hai để rút gọn biểu thức B.

3) Tính \(\frac{A}{B}\).

Giải bất phương trình \(\frac{A}{B} < \frac{1}{2}\), biện luận để tìm giá trị của \(x\).

Kết hợp điều kiện xác định để giá trị thoả mãn của \(x\).

Lời giải:

1) Thay \(x = 9\) (TMĐK) vào biểu thức, ta được:\(A = \frac{{\sqrt 9  + 2}}{{\sqrt 9  - 2}} = \frac{{3 + 2}}{{3 - 2}} = \frac{5}{1} = 5\)

Vậy khi \(x = 9\) thì \(A = 5\)

2)

\(B = \frac{{x + \sqrt x  - 4}}{{x - 2\sqrt x }} - \frac{1}{{\sqrt x  - 2}}\)

\(B = \frac{{x + \sqrt x  - 4}}{{\sqrt x \left( {\sqrt x  - 2} \right)}} - \frac{1}{{\sqrt x  - 2}}\)

\(B = \frac{{x + \sqrt x  - 4}}{{\sqrt x \left( {\sqrt x  - 2} \right)}} - \frac{{\sqrt x }}{{\sqrt x \left( {\sqrt x  - 2} \right)}}\)

\(B = \frac{{x + \sqrt x  - 4 - \sqrt x }}{{\sqrt x \left( {\sqrt x  - 2} \right)}}\)

\(B = \frac{{x - 4}}{{\sqrt x \left( {\sqrt x  - 2} \right)}}\)

\(B = \frac{{\left( {\sqrt x  + 2} \right)\left( {\sqrt x  - 2} \right)}}{{\sqrt x \left( {\sqrt x  - 2} \right)}}\)

\(B = \frac{{\sqrt x  + 2}}{{\sqrt x }}\)

Vậy \(B = \frac{{\sqrt x  + 2}}{{\sqrt x }}\) (đpcm)

3) Ta có:

\(\frac{A}{B} = \frac{{\sqrt x  + 2}}{{\sqrt x  - 2}}:\frac{{\sqrt x  + 2}}{{\sqrt x }} = \frac{{\sqrt x  + 2}}{{\sqrt x  - 2}} \cdot \frac{{\sqrt x }}{{\sqrt x  + 2}} = \frac{{\sqrt x }}{{\sqrt x  - 2}}\)

Để \(\frac{A}{B} < \frac{1}{2}\)

\(\frac{{\sqrt x }}{{\sqrt x  - 2}} < \frac{1}{2}\)

\(\frac{{\sqrt x }}{{\sqrt x  - 2}} - \frac{1}{2} < 0\)

\(\frac{{2\sqrt x  - \left( {\sqrt x  - 2} \right)}}{{2\left( {\sqrt x  - 2} \right)}} < 0\)

\(\frac{{2\sqrt x  - \sqrt x  + 2}}{{2\left( {\sqrt x  - 2} \right)}} < 0\)

\(\frac{{\sqrt x  + 2}}{{2\left( {\sqrt x  - 2} \right)}} < 0\)

Mà \(\sqrt x  + 2 > 0\), mọi \(x\).

Nên \(2\left( {\sqrt x  - 2} \right) < 0\)

\(\sqrt x  - 2 < 0\)

\(\sqrt x  < 2\)

\(x < 4\)

Kết hợp với ĐKXĐ \(x > 0,x \ne 4\), ta được: \(0 < x < 4\).

Mà x là số nguyên dương lớn nhất nên \(x = 3\).

Vậy \(x = 3\) để thỏa mãn đề bài.

Câu III (2,5 điểm)

1) Một ô tô đi từ Hà Nội đến Hải Phòng với vận tốc trung bình 60 km/h. Khi từ Hải Phòng về Hà Nội trên cùng quãng đường đó, do điều kiện thời tiết xấu nên ô tô đi với vận tốc trung bình 40 km/h. Biết thời gian ô tô đi từ Hà Nội đến Hải Phòng ít hơn thời gian ô tô đi từ Hải Phòng về Hà Nội là 1 giờ, tính độ dài quãng đường ô tô đã đi từ Hà Nội đến Hải Phòng.

2) Để chuẩn bị cho năm học mới, bạn Quốc đến cửa hàng mua một chiếc ba lô và một chiếc máy tính cầm tay với tổng giá tiền niêm yết là 885 nghìn đồng. Hiện tại, cửa hàng đó đang triển khai chương trình giảm giá cho học sinh, sinh viên nên giá tiền của một chiếc ba lô giảm 20% và giá tiền của một chiếc máy tính cầm tay giảm 25% so với giá tiền niêm yết. Vì vậy, bạn Quốc chỉ phải trả 682 nghìn đồng khi mua hai sản phẩm này. Hỏi giá tiền niêm yết của một chiếc ba lô và giá tiền niêm yết của một chiếc máy tính cầm tay là bao nhiêu?

3) Biết phương trình bậc hai \({x^2} + 8x - 6 = 0\) có hai nghiệm \({x_1}\) và \({x_2}\), tìm tất cả giá trị của m thỏa mãn \(\frac{{70 - mx_1^2}}{{{x_2}}} = {x_1} + m{x_2}\).

Phương pháp:

1) Gọi độ dài quãng đường từ Hà Nội đến Hải Phòng là x (km, x > 0)

Biểu diễn thời gian ô tô đi từ Hà Nội đến Hải Phòng và thời gian ô tô đi từ Hải Phòng về Hà Nội theo \(x\).

Vì thời gian ô tô đi từ Hà Nội đến Hải Phòng ít hơn thời gian ô tô đi từ Hải Phòng về Hà Nội là 1 giờ nên ta lập được phương trình.

Giải phương trình để tìm \(x\).

Kiểm tra điều kiện và kết luận.

2) Gọi giá tiền niêm yết của một ba lô là x (nghìn đồng) (0 < x < 885)

Gọi giá tiền niêm yết của một máy tính là y (nghìn đồng) (0 < y < 885)

Xác định phương trình tổng giá tiền niêm yết của hai món đồ là 885 nghìn đồng.

Biểu diễn giá tiền của ba lô, máy tính sau khi giảm giá rồi xác định phương trình tổng giá tiền của hai món đồ sau khi giảm giá là 682 nghìn đồng.

Ta lập được hệ phương trình.

Giải hệ phương trình, kiểm tra điều kiện và kết luận.

3) Áp dụng định lí Viète.

Biến đổi để xuất hiện \({x_1} + {x_2},{x_1}{x_2}\) và thay định lí Viète vào để tìm m.

Lời giải:

1) Gọi độ dài quãng đường từ Hà Nội đến Hải Phòng là x (km, x > 0)

Thời gian ô tô đi từ Hà Nội đến Hải Phòng là \(\frac{x}{{60}}\) (h)

Thời gian ô tô đi từ Hải Phòng về Hà Nội là \(\frac{x}{{40}}\) (h)

Vì thời gian ô tô đi từ Hà Nội đến Hải Phòng ít hơn thời gian ô tô đi từ Hải Phòng về Hà Nội là 1 giờ nên ta có phương trình:\(\frac{x}{{40}} - \frac{x}{{60}} = 1\)

Giải phương trình ta được: \(x = 120\) (TKĐK)

Vậy độ dài quãng đường từ Hà Nội đến Hải Phòng là 120 km.

2) Gọi giá tiền niêm yết của một ba lô là x (nghìn đồng) (0 < x < 885)

Gọi giá tiền niêm yết của một máy tính là y (nghìn đồng) (0 < y < 885)

Tổng giá tiền niêm yết của hai món đồ là 885 nghìn đồng nên ta có phương trình:\(x + y = 885\)

Giá tiền của ba lô sau khi giảm giá là: \(x - 20{\rm{\% }} \cdot x = 0,8x\) (nghìn đồng)

Giá tiền của máy tính sau khi giảm giá là: \(y - 25{\rm{\% }} \cdot y = 0,75y\) (nghìn đồng)

Tổng giá tiền của hai món đồ sau khi giảm giá là 682 nghìn đồng nên ta có phương trình:\(0,8x + 0,75y = 682\)

Khi đó ta có hệ phương trình:\(\left\{ {\begin{array}{*{20}{l}}{x + y = 885}\\{0,8x + 0,75y = 682}\end{array}} \right.\)

Giải hệ phương trình ta được:\(\left\{ {\begin{array}{*{20}{l}}{x = 365}\\{y = 520}\end{array}} \right.\) (thỏa mãn điều kiện)

Vậy giá tiền niêm yết của một ba lô là 365 nghìn đồng, giá tiền của một máy tính là 520 nghìn đồng.

3) Biết phương trình bậc hai \({x^2} + 8x - 6 = 0\) có hai nghiệm \({x_1}\) và \({x_2}\).

Áp dụng định lí Viète, ta có \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} =  - 8}\\{{x_1}{x_2} =  - 6}\end{array}} \right.\)

Do \({x_1}{x_2} =  - 6 \ne 0\) nên \({x_1} \ne 0;{x_2} \ne 0\)

Ta có:

\(\frac{{70 - mx_1^2}}{{{x_2}}} = {x_1} + m{x_2}\)

\(\begin{array}{l}70 - mx_1^2 = \left( {{x_1} + m{x_2}} \right){x_2}\\70 - mx_1^2 = {x_1}{x_2} + mx_2^2\\70 - mx_1^2 - {x_1}{x_2} - mx_2^2 = 0\end{array}\)

\(\begin{array}{l}70 - m\left( {x_1^2 + x_2^2} \right) - {x_1}{x_2} = 0\\70 - m\left[ {{{\left( {{x_1} + {x_2}} \right)}^2} - 2{x_1}{x_2}} \right] - {x_1}{x_2} = 0\\70 - m\left[ {{{\left( { - 8} \right)}^2} - 2\left( { - 6} \right)} \right] - \left( { - 6} \right) = 0\end{array}\)

\(\begin{array}{l}70 - m\left[ {64 + 12} \right] + 6 = 070 - 76m + 6 = 0\\76 - 76m = 0\\76m = 76\\m = 1\end{array}\)

Vậy \(m = 1\) thỏa mãn yêu cầu đề bài

Câu IV (4,0 điểm)

1) Gia đình bạn Khánh đang sử dụng một thùng đựng nước dạng hình trụ với bán kính đáy bằng 50 cm và chiều cao bằng 150 cm. Thùng đựng nước được đặt thẳng đứng trên mặt sàn như hình minh họa bên. (Lấy \(\pi  \approx 3,14\) và coi chiều dày của thùng không đáng kể).

a) Tính diện tích xung quanh của thùng đựng nước.

b) Sau một thời gian gia đình bạn Khánh sử dụng nước trong thùng thì mực nước còn lại đã thấp hơn 40 cm sơ với mực nước ban đầu. Tính thể tích nước trong thùng mà gia đình bạn Khánh đã sử dụng trong khoảng thời gian đó.

2) Cho tam giác ABC có ba góc nhọn (AB < AC), nội tiếp đường tròn (O). Đường cao AD của tam giác ABC cắt đường tròn (O) tại điểm E (E khác A). Gọi K là chân đường vuông góc kẻ từ điểm E đến đường thẳng AB.

a) Chứng minh bốn điểm E, D, B, K cùng thuộc một đường tròn.

b) Đường thẳng AO cắt đường thẳng BC tại điểm S. Chứng minh EA là tia phân giác của góc CEK và AB. AC = AE. AS.

c) Gọi H là trực tâm của tam giác ABC và I là trung điểm của đoạn thẳng AB. Chứng minh đường thẳng SI vuông góc với đường thẳng HK.

Phương pháp:

1)

a) Tính diện tích xung quanh của thùng đựng nước: \(2\pi Rh\)

b) Thể tích nước đã sử dụng là: \(\pi {R^2}h - \pi {R^2}h{\rm{'}}\)

2)

a) Chứng minh \(\Delta BKE\) vuông tại K, \(\Delta BDE\) vuông tại D nên bốn điểm E,D,B,K cùng thuộc đường tròn đường kính BE

b) Chứng minh \(\angle BAD = \angle MAC\)

\(\angle ACS = \angle AEB\) (hai góc nội tiếp đường tròn tâm O cùng chắn cung AB)

Suy ra $\Delta ABE\backsim \Delta ASC$ (g-g)

Do đó $AB\cdot AC=AE\cdot AS$

c) Chứng minh $\Delta EKD\backsim BAS$ (g.g)

Lại có D và I là trung điểm của EH và AB

Chứng minh $\Delta EKH\backsim \Delta BIS$ (c.g.c)

Suy ra \(\angle BIS = \angle EKH\)

Suy ra \(\angle BIS + \angle AKH = \angle AKE = {90^ \circ }\)

Suy ra \(SI \bot HK\)

Lời giải:

1)

a) Diện tích xung quanh của thùng đựng nước là

\(2\pi Rh \approx 2 \cdot 3,14 \cdot 50 \cdot 150 = 47100\) (cm²)

b) Thể tích nước đã sử dụng là:

\(\pi {R^2}h - \pi {R^2}h{\rm{'}} = \pi {R^2}\left( {h - h{\rm{'}}} \right) \approx 3,14 \cdot {50^2} \cdot 40 = 3,14 \cdot 2500 \cdot 40 = 314000\) (cm³)

2)

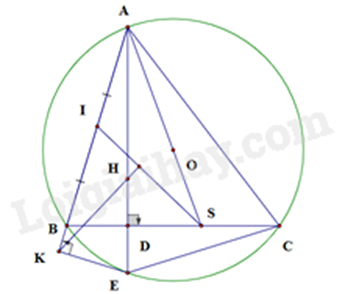
a) Xét \(\Delta ABC\) có AD là đường cao suy ra \(AD \bot BC\) hay \(AE \bot BC\)

Suy ra \(\angle BDE = {90^ \circ }\) suy ra tam giác BDE vuông tại D

Có K là chân đường vuông góc kẻ từ E đến đường thẳng AB

Suy ra \(KE \bot AB\) nên \(\angle BKE = {90^ \circ }\) suy ra tam giác BKE vuông tại K

Xét \(\Delta BDE\) vuông tại D

Suy ra ba điểm B, D, E cùng thuộc đường tròn đường kính BE. (1)

Xét \(\Delta BKE\) vuông tại K

Suy ra ba điểm B, K, E cùng thuộc đường tròn đường kính BE. (2)

Từ (1) và (2) suy ra bốn điểm E, D, B, K cùng thuộc đường tròn đường kính BE.

b)

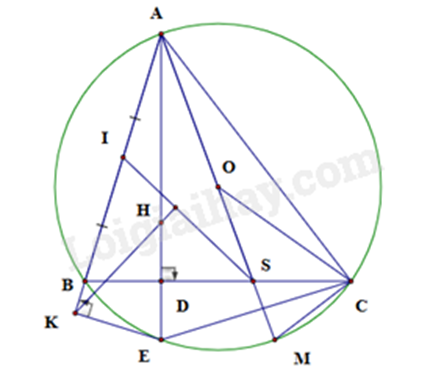
Ta có tứ giác EDBK nội tiếp (cmt)

\(\angle KED + \angle KBD = {180^ \circ }\)

Mà \(\angle ABD + \angle KBD = {180^ \circ }\) (hai góc kề bù)

Nên \(\angle KED = \angle ABD\) hay \(\angle KEA = \angle ABC\)

Xét (O) có \(\angle ABC = \angle AEC\) (hai góc nội tiếp cùng chắn cung AC)

Suy ra \(\angle KEA = \angle AEC\)

Mà tia EA nằm giữa 2 tia EK và EC

Nên EA là phân giác của \(\angle CEK\)

Kéo dài AO cắt (O) tại điểm thứ 2 là M

Suy ra \(\angle ACM = {90^ \circ }\) (góc nội tiếp chắn nửa đường tròn)

\(\Delta AMC\) vuông tại C nên \(\angle CAM + \angle CMA = {90^ \circ }\)

Xét (O) có \(\angle AMC = \angle ABC\) (hai góc nội tiếp cùng chắn cung AC)

Xét \(\Delta ABD\) vuông tại D có \(\angle ABD + \angle BAD = {90^ \circ }\)

Suy ra \(\angle BAD = \angle MAC\)

Xét \(\Delta ABE\) và \(\Delta ASC\)

\(\angle BAE = \angle CAS\) (chứng minh trên)

\(\angle ACS = \angle AEB\) (hai góc nội tiếp đường tròn tâm O cùng chắn cung AB)

Suy ra $\Delta ABE\backsim \Delta ASC$ (g-g)

\(\begin{array}{l}\frac{{AB}}{{AS}} = \frac{{AE}}{{AC}}\\AB \cdot AC = AE \cdot AS\end{array}\)

c) Xét (O): \(\angle ABC = \angle AEC\) (góc nội tiếp cùng chắn AC)

\(\angle AEK = \angle AEC\) (cmt)

Suy ra \(\angle ABC = \angle AEK\)

Chứng minh được: \(\angle BAS = \angle EAC = \angle EBD = \angle EKD\)

Suy ra $\Delta EKD\backsim \Delta BAS$ (g.g)

Lại có D và I là trung điểm của EH và AB

Chứng minh được: \(\Delta EKH\backsim \Delta BIS\) (c.g.c)

Suy ra \(\angle BIS = \angle EKH\)

Suy ra $\angle BIS+\angle AKH=\angle AKE={{90}^{\circ }}$

Suy ra \(SI \bot HK\) (đpcm)

Câu V (0,5 điểm)

Một công ty kinh doanh trong lĩnh vực vận tải đang vận hành một đội gồm 35 xe chở hàng cùng loại, với lợi nhuận trung bình của mỗi xe là 1 triệu đồng một ngày. Để mở rộng mô hình kinh doanh, công ty dự định bổ sung một số xe chở hàng cùng loại với xe đang vận hành. Công ty đã tiến hành khảo sát và phân tích thị trường, kết quả cho thấy: cứ bổ sung một xe chở hàng cùng loại vào hoạt động thì lợi nhuận trung bình của mỗi xe trong cả đội lại giảm đi 20 nghìn đồng một ngày. Hỏi công ty nên bổ sung bao nhiêu xe chở hàng cùng loại để lợi nhuận trung bình mỗi ngày của đội xe là lớn nhất?

Phương pháp:

Đổi 1 triệu đồng = 1 000 nghìn đồng

Gọi x là số xe được bổ sung (\(x > 0;x \in {\mathbb{N}^{\rm{*}}}\))

Biểu diễn số xe sau khi được bổ sung, lợi nhuận của 1 xe sau trong 1 ngày khi bổ sung suy ra lợi nhuận của toàn đội xe trong 1 ngày.

Biện luận để tìm giá trị lớn nhất của P(x).

Lời giải:

Cách 1:

Đổi 1 triệu đồng = 1 000 nghìn đồng

Gọi x là số xe được bổ sung (\(x > 0;x \in {\mathbb{N}^{\rm{*}}}\))

Số xe sau khi được bổ sung là: \(x + 35\) (xe)

Lợi nhuận của 1 xe sau trong 1 ngày khi bổ sung là: \(1000--20x\) (nghìn đồng)

Lợi nhuận của toàn đội xe trong 1 ngày là:\(P\left( x \right) = \left( {35 + x} \right)\left( {1000--20x} \right)\)

\(\begin{array}{l}P\left( x \right) = \left( {35 + x} \right)\left( {1000 - 20x} \right)\\P\left( x \right) =  - 20{x^2} + 300x + 35000\end{array}\)

\(\begin{array}{l}P\left( x \right) =  - 20\left( {{x^2} - 15x - 1750} \right)\\P\left( x \right) =  - 20{\left( {x - 7,5} \right)^2} + 36125\end{array}\)

Vì \({\left( {x - 7,5} \right)^2} \ge 0\) với mọi x, nên \( - 20{\left( {x - 7,5} \right)^2} \le 0\).

Do đó, \(P\left( x \right) \le 36125\).

Giá trị lớn nhất của \(P\left( x \right)\) đạt được khi \({\left( {x--7,5} \right)^2}\) nhỏ nhất.

Do x là số tự nhiên, ta xét hai giá trị tự nhiên gần 7,5 nhất là \(x = 7\) và \(x = 8\)

Khi \(x = 7\), ta có \({\left( {7--7,5} \right)^2} = {\left( { - 0,5} \right)^2} = 0,25\).

Khi \(x = 8\), ta có \({\left( {8--7,5} \right)^2} = {\left( {0,5} \right)^2} = 0,25\).

Cả hai giá trị \(x = 7\) và \(x = 8\) đều cho \({\left( {x--7,5} \right)^2}\) một giá trị nhỏ nhất là 0,25.

Vậy, công ty nên bổ sung 7 xe hoặc 8 xe để lợi nhuận mỗi ngày là lớn nhất.

Cách 2:

Đổi 1 triệu đồng = 1 000 nghìn đồng

Gọi số xe được công ty bổ sung là: x (xe) ( Điều kiện: \(x \in {\mathbb{N}^{\rm{*}}}\) )

Số xe sau khi được bổ sung là: \(x + 35\) (xe)

Lợi nhuận của một xe trong 1 ngày sau khi bổ sung là: \(1000--20x\) (nghìn đồng)

Lợi nhuận của cả đội xe trong 1 ngày là:

\(\begin{array}{l}P\left( x \right) = \left( {35 + x} \right)\left( {1000--20x} \right)\\P\left( x \right) =  - 20{x^2} + 300x + 35000\end{array}\)

\(\begin{array}{l}P\left( x \right) =  - 20{x^2} + 140x + 160x - 1120 + 36120\\P\left( x \right) =  - 20x\left( {x - 7} \right) + 160\left( {x - 7} \right) + 36120\\P\left( x \right) =  - 20\left( {x - 7} \right)\left( {x - 8} \right) + 36120\end{array}\)

- Với \(x < 7,x \in {\mathbb{N}^{\rm{*}}}\) thì \(\left( {x - 7} \right)\left( {x--8} \right) > 0\)

Do đó, \( - 20\left( {x - 7} \right)\left( {x--8} \right) + 36120 < 36120\)

- Với \(x = 7\) hoặc \(x = 8,x \in {\mathbb{N}^{\rm{*}}}\) thì \(\left( {x - 7} \right)\left( {x--8} \right) = 0\)

Do đó, \( - 20\left( {x - 7} \right)\left( {x--8} \right) + 36120 = 36120\)

- Với \(x > 8,x \in {\mathbb{N}^{\rm{*}}}\) thì \(\left( {x - 7} \right)\left( {x--8} \right) > 0\)

Do đó, \( - 20\left( {x - 7} \right)\left( {x--8} \right) + 36120 < 36120\)

Vậy, công ty nên bổ sung 7 xe hoặc 8 xe để lợi nhuận mỗi ngày là lớn nhất.