Đề thi vào 10 môn Toán Hà Nội năm 2020
Tải vềBài I (2 điểm): Cho hai biểu thức
Đề bài
Bài I (2 điểm): Cho hai biểu thức \(A = \dfrac{{\sqrt x + 1}}{{\sqrt x + 2}}\) và \(B = \dfrac{3}{{\sqrt x - 1}} - \dfrac{{\sqrt x + 5}}{{x - 1}}\) với \(x \ge 0,\,\,x \ne 1\).
1) Tính giá trị của biểu thức \(A\) khi \(x = 4\).
2) Chứng minh \(B = \dfrac{2}{{\sqrt x + 1}}\).
3) Tìm tất cả các giá trị của \(x\) để biểu thức \(P = 2A.B + \sqrt x \) đạt giá trị nhỏ nhất.
Bài II (2 điểm):
1) Giải bài toán san bằng cách lập phương trình hoặc hệ phương trình.
Quãng đường từ nhà An đến nhà Bình dài 3 km. Buổi sáng, An đi bộ từ nhà An đến nhà Bình. Buổi chiều cùng ngày, An đi xe đạp từ nhà Bình về nhà An trên cùng quãng đường đó với vận tốc lớn hơn vận tốc đi bộ của An là 9km/h. Tính vận tốc đi bộ của An, biết thời gian đi buổi chiều ít hơn thời gian đi buổi sáng là 45 phút. (Giả định rằng An đi bộ với vận tốc không đổi trên toàn bộ quãng đường đó).
2) Một quả bóng bàn có dạng một hình cầu có bán kính bằng 2 cm. Tính diện tích bề mặt của quả bóng bàn đó (lấy \(\pi \approx 3,14\)).
Bài III (2,5 điểm):
1) Giải hệ phương trình \(\left\{ \begin{array}{l}2x + \dfrac{3}{{y - 1}} = 5\\4x - \dfrac{1}{{y - 1}} = 3\end{array} \right.\)
2) Trong mặt phẳng tọa độ \(Oxy\), xét đường thẳng \(\left( d \right):y = mx + 4\) với \(m \ne 0.\)
a) Gọi \(A\) là giao điểm của đường thẳng \(\left( d \right)\) và trục \(Oy.\) Tìm tọa độ của điểm \(A.\)
b) Tìm tất cả giá trị của \(m\) để đường thẳng \(\left( d \right)\) cắt trục \(Ox\) tại điểm \(B\) sao cho tam giác \(OAB\) là tam giác cân.
Bài IV (3 điểm): Cho tam giác ABC có ba góc nhọn và đường cao BE. Gọi H và K lần lượt là chân các đường vuông góc kẻ từ điểm E đến các đường thẳng AB và BC.
1) Chứng minh tứ giác BHEK là tứ giác nội tiếp.
2) Chứng minh \(BH.BA = BK.BC\).
3) Gọi F là chân đường vuông góc kẻ từ điểm C đến đường thẳng AB và I là trung điểm của đoạn thẳng EF. Chứng minh ba điểm H, I, K là ba điểm thẳng hàng.
Bài V (0,5 điểm):
Giải phương trình \(\sqrt x + \sqrt {3x - 2} = {x^2} + 1\)
Lời giải chi tiết
|
Bài I (2,0 điểm) Cho hai biểu thức \(A = \dfrac{{\sqrt x + 1}}{{\sqrt x + 2}}\) và \(B = \dfrac{3}{{\sqrt x - 1}} - \dfrac{{\sqrt x + 5}}{{x - 1}}\) với \(x \ge 0,\,\,x \ne 1\). |
1) Tính giá trị của biểu thức \(A\) khi \(x = 4\).
Thay \(x = 4\,\,\left( {TMDK} \right)\) vào biểu thức \(A\) ta có: \(A = \dfrac{{\sqrt 4 + 1}}{{\sqrt 4 + 2}} = \dfrac{{2 + 1}}{{2 + 2}} = \dfrac{3}{4}\).
Vậy khi \(x = 4\) thì \(A = \dfrac{3}{4}\).
2) Chứng minh \(B = \dfrac{2}{{\sqrt x + 1}}\).
Với \(x \ge 0,\,\,x \ne 1\) ta có:
\(\begin{array}{l}B = \dfrac{3}{{\sqrt x - 1}} - \dfrac{{\sqrt x + 5}}{{x - 1}}\\B = \dfrac{3}{{\sqrt x - 1}} - \dfrac{{\sqrt x + 5}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}\\B = \dfrac{{3\left( {\sqrt x + 1} \right) - \left( {\sqrt x + 5} \right)}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}\\B = \dfrac{{3\sqrt x + 3 - \sqrt x - 5}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}\\B = \dfrac{{2\sqrt x - 2}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}\\B = \dfrac{{2\left( {\sqrt x - 1} \right)}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}\\B = \dfrac{2}{{\sqrt x + 1}}\,\,\,\left( {dpcm} \right)\end{array}\)
Vậy với \(x \ge 0,\,\,x \ne 1\) thì \(B = \dfrac{2}{{\sqrt x + 1}}\).
3) Tìm tất cả các giá trị của \(x\) để biểu thức \(P = 2A.B + \sqrt x \) đạt giá trị nhỏ nhất.
Với \(x \ge 0,\,\,x \ne 1\) ta có:
\(\begin{array}{l}P = 2A.B + \sqrt x \\P = 2.\dfrac{{\sqrt x + 1}}{{\sqrt x + 2}}.\dfrac{2}{{\sqrt x + 1}} + \sqrt x \\P = \dfrac{4}{{\sqrt x + 2}} + \sqrt x \\P = \sqrt x + 2 + \dfrac{4}{{\sqrt x + 2}} - 2\end{array}\)
Áp dụng BĐT Cô-si cho hai số dương \(\sqrt x + 2\) và \(\dfrac{4}{{\sqrt x + 2}}\) ta có:
\(\sqrt x + 2 + \dfrac{4}{{\sqrt x + 2}} \ge 2\sqrt {\left( {\sqrt x + 2} \right).\dfrac{4}{{\sqrt x + 2}}} = 2\sqrt 4 = 4\)
\(\begin{array}{l} \Rightarrow \sqrt x + 2 + \dfrac{4}{{\sqrt x + 2}} - 2 \ge 2\\ \Rightarrow A \ge 2\end{array}\)
Dấu “=” xảy ra \( \Leftrightarrow \sqrt x + 2 = \dfrac{4}{{\sqrt x + 2}} \Leftrightarrow {\left( {\sqrt x + 2} \right)^2} = 4\) \( \Leftrightarrow \sqrt x + 2 = 2\,\,\left( {Do\,\,\sqrt x + 2 \ge 2\,\,\forall x \ge 0,\,\,x \ne 1} \right)\).
\( \Leftrightarrow \sqrt x = 0 \Leftrightarrow x = 0\,\,\,\left( {tm} \right)\).
Vậy biểu thức \(P\) đạt giá trị nhỏ nhất bằng \(2\) khi và chỉ khi \(x = 0\).
Bài II (2,0 điểm)
|
1) Giải bài toán san bằng cách lập phương trình hoặc hệ phương trình. Quãng đường từ nhà An đến nhà Bình dài 3 km. Buổi sáng, An đi bộ từ nhà An đến nhà Bình. Buổi chiều cùng ngày, An đi xe đạp từ nhà Bình về nhà An trên cùng quãng đường đó với vận tốc lớn hơn vận tốc đi bộ của An là 9km/h. Tính vận tốc đi bộ của An, biết thời gian đi buổi chiều ít hơn thời gian đi buổi sáng là 45 phút. (Giả định rằng An đi bộ với vận tốc không đổi trên toàn bộ quãng đường đó). |
Gọi vận tốc đi bộ của An là \(x\,\,\left( {km/h} \right),\,\,\left( {x > 0} \right).\)
\( \Rightarrow \) Thời gian An đi bộ hết quãng đường từ nhà An đến nhà Bình là: \(\dfrac{3}{x}\,\,\,\left( h \right).\)
Vận tốc đi xe đạp của An hơn vận tốc đi bộ là \(9\,\,km/h\) nên vận tốc đi xe đạp là: \(x + 9\,\,\left( {km/h} \right).\)
\( \Rightarrow \) Thời gian An đi xe đạp hết quãng đường từ nhà Bình về nhà An là: \(\dfrac{3}{{x + 9}}\,\,\,\left( h \right).\)
Vì An đi xe đạp nhanh hơn đi bộ là 45 phút \( = \dfrac{{45}}{{60}} = \dfrac{3}{4}\,\,\left( h \right)\) nên ta có phương trình:
\(\begin{array}{l}\,\,\,\,\,\,\,\dfrac{3}{x} - \dfrac{3}{{x + 9}} = \dfrac{3}{4}\\ \Leftrightarrow \dfrac{1}{x} - \dfrac{1}{{x + 9}} = \dfrac{1}{4}\\ \Leftrightarrow 4\left( {x + 9} \right) - 4x = x\left( {x + 9} \right)\\ \Leftrightarrow 4x + 36 - 4x = {x^2} + 9x\\ \Leftrightarrow {x^2} + 9x - 36 = 0\\ \Leftrightarrow {x^2} + 12x - 3x - 36 = 0\\ \Leftrightarrow x\left( {x + 12} \right) - 3\left( {x + 12} \right) = 0\\ \Leftrightarrow \left( {x - 3} \right)\left( {x + 12} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 3 = 0\\x + 12 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 3\,\,\,\,\,\,\,\,\,\,\left( {tm} \right)\\x = - 12\,\,\,\left( {ktm} \right)\end{array} \right.\end{array}\)
Vậy vận tốc đi bộ của An là \(3km/h.\)
| 2) Một quả bóng bàn có dạng một hình cầu có bán kính bằng 2 cm. Tính diện tích bề mặt của quả bóng bàn đó (lấy \(\pi \approx 3,14\)). |
Diện tích bề mặt của quả bóng bàn đó là: \(S = 4\pi {R^2} \approx 4.3,{14.2^2} \approx 50,24\,\,\left( {c{m^2}} \right)\).
Vậy diện tích bề mặt của quả bóng bàn là \(S \approx 50,24\,\,c{m^2}\).
Bài III (2, 5 điểm)
| 1) Giải hệ phương trình \(\left\{ \begin{array}{l}2x + \dfrac{3}{{y - 1}} = 5\\4x - \dfrac{1}{{y - 1}} = 3\end{array} \right.\) |
Điều kiện: \(y \ne 1.\)
Đặt \(\dfrac{1}{{y - 1}} = u\,\,\,\left( {u \ne 0} \right)\) ta có hệ phương trình:
\(\begin{array}{l}\,\,\,\,\,\,\left\{ \begin{array}{l}2x + 3u = 5\\4x - u = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4x + 6u = 10\\4x - u = 3\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}7u = 7\\4x - u = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}u = 1\\4x - 1 = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}u = 1\,\,\,\,\left( {tm} \right)\\x = 1\end{array} \right.\end{array}\)
Với \(u = 1\) ta có: \(\dfrac{1}{{y - 1}} = 1 \Rightarrow y - 1 = 1 \Leftrightarrow y = 2\,\,\,\left( {tm} \right)\).
Vậy hệ phương trình đã cho có nghiệm duy nhất \(\left( {x;y} \right) = \left( {1;2} \right)\).
| 2) Trong mặt phẳng tọa độ \(Oxy\), xét đường thẳng \(\left( d \right):y = mx + 4\) với \(m \ne 0.\) |
a) Gọi \(A\) là giao điểm của đường thẳng \(\left( d \right)\) và trục \(Oy.\) Tìm tọa độ của điểm \(A.\)
Vì \(A\) là giao điểm của của đường thẳng \(\left( d \right)\) và trục \(Oy\) nên hoành độ điểm \(A\) là \({x_A} = 0\).
Gọi \(A\left( {0;{y_A}} \right)\)
Vì \(A\left( {0;{y_A}} \right) \in d\) nên ta có: \({y_A} = m.0 + 4 \Leftrightarrow {y_A} = 4\).
Vậy \(A\left( {0;4} \right)\) là giao điểm của đường thẳng \(\left( d \right)\) và trục \(Oy\).
b) Tìm tất cả giá trị của \(m\) để đường thẳng \(\left( d \right)\) cắt trục \(Ox\) tại điểm \(B\) sao cho tam giác \(OAB\) là tam giác cân.
Vì \(B\) là giao điểm của \(\left( d \right)\) cắt trục \(Ox\) nên tung độ điểm \(B\) là \({y_B} = 0\).
Gọi \(B\left( {{x_B};0} \right)\). Vì \(B\left( {{x_B};0} \right) \in \left( d \right)\) nên ta có: \(0 = m.{x_B} + 4\) \( \Leftrightarrow {x_B} = \dfrac{{ - 4}}{m}\) (vì \(m \ne 0\))
Suy ra \(B\left( {\dfrac{{ - 4}}{m};0} \right)\) . Do đó \(OB = \left| {\dfrac{{ - 4}}{m}} \right|\).
Theo câu a) ta có: \(A\left( {0;4} \right)\) nên \(OA = \left| 4 \right| = 4\).
Vì tam giác \(OAB\) cân tại \(O\) nên \(OA = OB \Leftrightarrow \left| {\dfrac{{ - 4}}{m}} \right| = 4\).
\( \Leftrightarrow \left[ \begin{array}{l}\dfrac{{ - 4}}{m} = 4\\\dfrac{4}{m} = 4\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}4m = - 4\\4m = 4\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = - 1\,\,\left( {tm} \right)\\m = 1\,\,\,\,\,\left( {tm} \right)\end{array} \right.\)
Vậy \(m = - 1;\,\,m = 1\) là các giá trị thỏa mãn yêu cầu đề bài.
Câu IV (3,0 điểm)
| Cho tam giác ABC có ba góc nhọn và đường cao BE. Gọi H và K lần lượt là chân các đường vuông góc kẻ từ điểm E đến các đường thẳng AB và BC. |
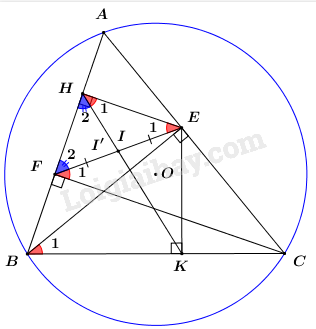
1) Chứng minh tứ giác BHEK là tứ giác nội tiếp.
Ta có:
\(\angle BHE = {90^0}\) (do \(EH \bot AB\))
\(\angle BKE = {90^0}\) (do \(EK \bot BC\))
Tứ giác \(BHEK\) có \(\angle BHE + \angle BKE = {90^0} + {90^0} = {180^0}\) nên là tứ giác nội tiếp (tứ giác có tổng hai góc đối bằng \({180^0}\)) (đpcm)
2) Chứng minh \(BH.BA = BK.BC\).
Theo câu a) tứ giác \(BHEK\) nội tiếp nên \(\angle BKH = \angle BEH\) (cùng chắn cung \(BH\))
Ta có:
\(\angle BEH + \angle EBH = {90^0}\) (do tam giác \(BHE\) vuông tại \(H\)).
\(\angle BAE + \angle EBH = {90^0}\) (do tam giác \(ABE\) vuông tại \(E\)).
Nên \(\angle BEH = \angle BAE\) (cùng phụ với \(\angle EBH\)).
Mà \(\angle BKH = \angle BEH\) (cmt) nên \(\angle BKH = \angle BAE\,\,\,\left( { = \angle BEH} \right)\).
Xét \(\Delta BHK\) và \(\Delta BCA\) có:
\(\angle ABC\) chung
\(\angle BKH = \angle BAE = \angle BAC\) (cmt)
\( \Rightarrow \Delta BHK \sim \Delta BCA\,\,\left( {g.g} \right)\)
\( \Rightarrow \dfrac{{BH}}{{BC}} = \dfrac{{BK}}{{BA}}\) (hai cạnh tương ứng)
\( \Rightarrow BH.BA = BK.BC\) (đpcm).
3) Gọi F là chân đường vuông góc kẻ từ điểm C đến đường thẳng AB và I là trung điểm của đoạn thẳng EF. Chứng minh ba điểm H, I, K là ba điểm thẳng hàng.
Cách 1:
Nối \(H\) và \(K.\)
Xét \(\Delta BHK\) và \(\Delta BCA\) ta có:
\(\begin{array}{l}\angle ABC\,\,\,\,chung\\\dfrac{{BH}}{{BC}} = \dfrac{{BK}}{{BA}}\,\,\,\left( {do\,\,\,BA.BA = BK.BC} \right)\\ \Rightarrow \Delta BHK \sim \Delta BCA\,\,\,\,\left( {c - g - c} \right)\end{array}\)
\( \Rightarrow \angle BHK \sim \angle BCA\) (hai góc tương ứng) (1)
Xét tứ giác \(BFEC\) ta có:
\(\angle BFC = \angle BEC = {90^0}\)
Mà \(F,\,\,E\) là hai đỉnh kề nhau
\( \Rightarrow BFEC\) là tứ giác nội tiếp (dhnb).
\( \Rightarrow \angle BCE + \angle BFE = {180^0}\) (tính chất tứ giác nội tiếp).
Mà \(\angle AFE + \angle BFE = {180^0}\) (2 góc kề bù)
\( \Rightarrow \angle BCE = \angle AFE\,\,\,\,\left( 2 \right)\)
Từ (1) và (2) ta có: \(\angle BHK = \angle HFI.\)
Ta có: \(\Delta FHE\) vuông tại \(H\) có \(HI\) là đường trung tuyến ứng với cạnh huyền
\( \Rightarrow HI = \dfrac{1}{2}EF\) (tính chất đường trung tuyến ừng với cạnh huyền).
\( \Leftrightarrow HI = FI\)
\( \Rightarrow \Delta HIF\) cân tại \(I\) (dhnb \(\Delta \) cân)
\( \Rightarrow \angle FHI = \angle HFI\) (tính chất \(\Delta \) cân)
Mà \(\angle HFI = \angle BHK\)
\( \Rightarrow \angle FHI = \angle BHK\) \( \Rightarrow HI \equiv HK\)
\( \Rightarrow H,\,\,I,\,\,K\) thẳng hàng.
Cách 2:
Gọi \(I'\) là giao điểm của HK và EF.
Xét tứ giác \(BFEC\) có: \(\angle BFC = \angle BEC = {90^0}\,\,\left( {gt} \right)\) nên là tứ giác nội tiếp (tứ giác có hai đỉnh kề nhau cùng nhìn 1 cạnh các góc bằng nhau).
\( \Rightarrow \angle {B_1} = \angle {F_1}\) (hai góc nội tiếp cùng chắn cung \(EC\)).
Ta có: \(EH//CF\) (cùng vuông góc \(AB\))
\( \Rightarrow \angle {F_1} = \angle {E_1}\) (so le trong)
Do đó \(\angle {B_1} = \angle {E_1}\) (1).
Theo câu a, tứ giác \(BHEK\) nội tiếp nên \(\angle {B_1} = \angle {H_1}\) (hai góc nội tiếp cùng chắn cung \(EK\)) (2).
Từ (1) và (2) suy ra \(\angle {H_1} = \angle {E_1}\)
Tam giác \(I'HE\) có \(\angle {H_1} = \angle {E_1}\) nên là tam giác cân (định nghĩa).
\( \Rightarrow I'H = I'E\) (tính chất tam giác cân) (3)
Lại có:
\(\angle {H_1} + \angle {H_2} = \angle BHE = {90^0}\)
\(\angle {F_2} + \angle {E_1} = {90^0}\) (do tam giác \(HEF\) vuông tại \(H\)).
Nên \(\angle {H_2} = \angle {F_2}\) hay tam giác \(I'HF\) cân tại \(I'\) (định nghĩa).
\( \Rightarrow I'H = I'F\) (tính chất tam giác cân) (4)
Từ (3) và (4) suy ra \(I'E = I'F\) hay \(I'\) là trung điểm của \(EF\).
Do đó \(I' \equiv I\) nên ba điểm \(H,I,K\) thẳng hàng (đpcm).
Bài V (0, 5 điểm)
| Giải phương trình \(\sqrt x + \sqrt {3x - 2} = {x^2} + 1\) |
Điều kiện: \(x \ge \dfrac{2}{3}\)
Ta có:
\(\begin{array}{l}\,\,\,\,\,\,\,\sqrt x + \sqrt {3x - 2} = {x^2} + 1\\ \Leftrightarrow 2\sqrt x + 2\sqrt {3x - 2} = 2{x^2} + 2\\ \Leftrightarrow 2{x^2} - 2\sqrt x - 2\sqrt {3x - 2} + 2 = 0\\ \Leftrightarrow 2\left( {{x^2} - 2x + 1} \right) + 4x - 2\sqrt x - 2\sqrt {3x - 2} = 0\\ \Leftrightarrow 2{\left( {x - 1} \right)^2} + \left( {x - 2\sqrt x + 1} \right) + \left( {3x - 2 - 2\sqrt {3x - 2} + 1} \right) = 0\\ \Leftrightarrow 2{\left( {x - 1} \right)^2} + {\left( {\sqrt x - 1} \right)^2} + {\left( {\sqrt {3x - 2} - 1} \right)^2} = 0\end{array}\)
Vì \({\left( {x - 1} \right)^2} \ge 0;{\left( {\sqrt x - 1} \right)^2} \ge 0\) và \({\left( {\sqrt {3x - 2} - 1} \right)^2} \ge 0\) với mọi \(x \ge \dfrac{2}{3}\) nên
\(\begin{array}{l}2{\left( {x - 1} \right)^2} + {\left( {\sqrt x - 1} \right)^2} + {\left( {\sqrt {3x - 2} - 1} \right)^2} = 0\\ \Leftrightarrow \left\{ \begin{array}{l}x - 1 = 0\\\sqrt x - 1 = 0\\\sqrt {3x - 2} - 1 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\x = 1\\\sqrt {3x - 2} = 1\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = 1\\3x - 2 = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\x = 1\end{array} \right. \Leftrightarrow x = 1\,\,\,\,\left( {tm} \right)\end{array}\)
Vậy \(x = 1\) là nghiệm duy nhất của phương trình đã cho.













Danh sách bình luận