Đề thi vào 10 môn Toán Phú Thọ năm 2025

Đề bài

PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm).

Câu 1: Điều kiện xác định của căn thức \(\sqrt {x - 1} \) là

A. \(x > 1\).

B. \(x \ge 1\).

C. \(x < 1\).

D. \(x \le 1\).

Câu 2: Nghiệm của phương trình \(\left( {{x^2} + 3} \right)\left( {1 - x} \right) = 0\) là

A. \(x =  - 3;x = 1\).

B. \(x =  - 3;x =  - 1\).

C. \(x = 1\).

D. \(x =  - 3\).

Câu 3: Bất phương trình \(1 - 3x \le  - 4x + 3\) có bao nhiêu nghiệm là số tự nhiên?

A. 2.

B. 0.

C. 3.

D. 1.

Câu 4: Phương trình nào sau đây không phải là phương trình bậc nhất hai ẩn của \(x\) và \(y\)?

A. \(x + y = 1\).

B. \({x^2} - y = 1\).

C. \(x - y = 0\).

D. \( - 2x + y - 3 = 0\).

Câu 5: Hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{x - y = 3}\\{3x + y = 1}\end{array}} \right.\) có nghiệm là

A. \(\left( {x;y} \right) = \left( { - 1; - 2} \right)\).

B. \(\left( {x;y} \right) = \left( { - 1;2} \right)\).

C. \(\left( {x;y} \right) = \left( {1;2} \right)\).

D. \(\left( {x;y} \right) = \left( {1; - 2} \right)\).

Câu 6: Gọi \({x_1},{x_2}\) là hai nghiệm của phương trình \({x^2} - 2025x - 2026 = 0\) khi đó \({x_1} + {x_2} + {x_1}{x_2}\) bằng

A. -1.

B. 1.

C. -4051.

D. 4051.

Câu 7: Đồ thị hàm số \(y =  - 2{x^2}\) đi qua điểm nào trong các điểm dưới đây?

A. \(M\left( { - 2; - 8} \right)\).

B. \(N\left( {2; - 4} \right)\).

C. \(P\left( { - 2;8} \right)\).

D. \(Q\left( { - 2; - 4} \right)\).

Câu 8: Cho tam giác \(ABC\) vuông tại \(A\) có \(AB = 3cm\), \(AC = 4cm\), \(BC = 5cm\). Khi đó \({\rm{cos}}B\) bằng

A. \(\frac{3}{4}\).

B. \(\frac{3}{5}\).

C. \(\frac{4}{5}\).

D. \(\frac{4}{3}\).

Câu 9: Tại thời điểm tia nắng chiếu xuống mặt đất tạo với mặt đất một góc \({40^ \circ }\) thì chiều dài bóng cây đo được là \(25\) mét (minh họa bằng hình vẽ), giả sử cây thẳng đứng và mặt đất phẳng. Hỏi cây cao bao nhiêu mét (kết quả làm tròn đến hàng đơn vị)?

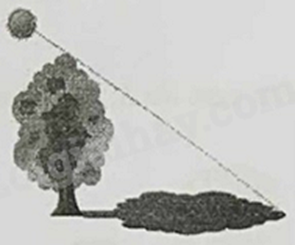
A. 30.

B. 19.

C. 21.

D. 16.

Câu 10: Một hộp có 30 quả bóng trong đó có 10 quả bóng được sơn màu vàng và các quả bóng còn lại được sơn màu xanh (các quả bóng có kích cỡ và khối lượng như nhau). Lấy ngẫu nhiên một quả bóng trong hộp. Xác suất của biến cố “Quả bóng lấy ra được sơn màu vàng” bằng

A. \(\frac{1}{{10}}\).

B. \(\frac{2}{3}\).

C. \(\frac{1}{2}\).

D. \(\frac{1}{3}\).

Câu 11: Cho tam giác \(ABC\) nội tiếp đường tròn \(\left( O \right)\) và \(\widehat {ABC} = {50^ \circ }\) như hình vẽ. Số đo \(\widehat {OAC}\) bằng

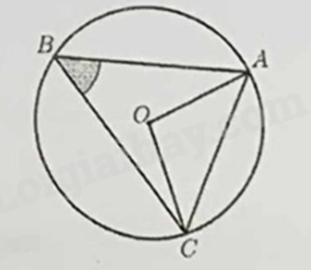
A. \({40^ \circ }\).

B. \({50^ \circ }\).

C. \({45^ \circ }\).

D. \({100^ \circ }\).

Câu 12: Cho đường tròn \(\left( {O;3cm} \right)\) và đường tròn \(\left( {O{\rm{'}};5cm} \right)\) tiếp xúc ngoài với nhau. Độ dài đoạn thẳng \(OO{\rm{'}}\) bằng

A. \(2cm\).

B. \(8cm\).

C. \(6cm\).

D. \(9cm\).

PHẦN II. TỰ LUẬN (7,0 điểm).

Câu 1: (1,5 điểm)

a) Giải phương trình \({x^2} + x - 6 = 0\).

b) Tính giá trị biểu thức \(A = 2\sqrt {28}  + 2\sqrt 9  - 4\sqrt 7 \).

c) Rút gọn biểu thức \(B = \left( {\frac{1}{{\sqrt a  - 3}} + \frac{2}{{\sqrt a  + 3}}} \right):\frac{{\sqrt a  - 1}}{{\sqrt a  - 3}}\) với \(a \ge 0,a \ne 1,a \ne 9\).

Câu 2: (2,0 điểm)

2.1.

a) Cho parabol \(\left( P \right):y = \left( {m - 2} \right){x^2}\) có đồ thị như hình vẽ. Tính giá trị biểu thức \(P = 4{m^2} - 2m + 5\).

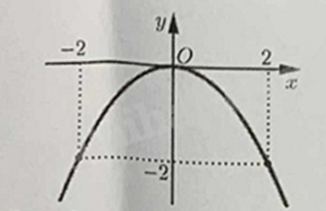
b) Cho phương trình \({x^2} - \left( {m - 1} \right)x - 3m - 6 = 0\), \(m\) là tham số. Tìm tất cả các giá trị của \(m\) để phương trình có hai nghiệm \({x_1},{x_2}\) thoả mãn điều kiện \(\left| {{x_1}} \right| = 5 + \left| {{x_2}} \right|\).

2.2. Nhân dịp khai trương, một siêu thị điện máy giảm giá mỗi tivi 20% và giảm giá mỗi máy giặt 15% so với giá niêm yết. Biết tổng số tiền bán một chiếc tivi và một chiếc máy giặt khi chưa giảm giá là 25 triệu đồng. Trong dịp này, bà Hiền đi mua một chiếc tivi và một chiếc máy giặt, bà phải trả tổng số tiền là 20,5 triệu đồng. Hỏi giá một chiếc tivi, một chiếc máy giặt khi chưa giảm giá là bao nhiêu tiền (đơn vị triệu đồng)?

Câu 3: (2,5 điểm)

Cho đường tròn \(\left( O \right)\) và dây cung \(AB\) khác đường kính. Điểm \(C\) nằm trên đường thẳng \(AB\) sao cho \(A\) nằm giữa \(B\) và \(C\). Vẽ đường kính \(DE\) của \(\left( O \right)\) vuông góc với dây cung \(AB\) tại \(K\) (\(D\) nằm trên cung lớn \(AB\)). Tia \(CD\) cắt \(\left( O \right)\) tại \(I\) (\(I\) khác \(D\)). Các dây \(AB\) và \(EI\) cắt nhau tại \(H\).

a) Chứng minh tứ giác \(DIHK\) nội tiếp đường tròn.

b) Chứng minh \(CI.CD = CH.CK\) và \(HA.IB = HB.IA\).

c) Vẽ \(DT\) vuông góc với đường thẳng \(AI\) tại \(T\), đường tròn đường kính \(CK\) cắt đoạn thẳng \(CD\) tại \(G\) (\(G\) khác \(D\)). Chứng minh \(K,G,T\) thẳng hàng.

Câu 4: (0,5 điểm) Một cây kem ốc quế có chiều cao 18 cm, phần thân là lớp vỏ làm bằng bánh quế có dạng là một hình nón, phần đỉnh có dạng là một nửa hình cầu có bán kính bằng 3 cm bằng với bán kính của đáy hình nón (minh họa bằng hình vẽ). Tính thể tích của cả cây kem.

Câu 5: (0,5 điểm) Giải hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{y\left( {{x^2} + x} \right) + 2 = {{\left( {{x^4} - {x^2}} \right)}^2}}\\{{x^2} + x - y = 2\sqrt {x + y} }\end{array}} \right.\)

----- HẾT -----

Lời giải

PHẦN I: CÂU TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN

Câu 1: Điều kiện xác định của căn thức \(\sqrt {x - 1} \) là

A. \(x > 1\).

B. \(x \ge 1\).

C. \(x < 1\).

D. \(x \le 1\).

Phương pháp:

Điều kiện xác định của \(\sqrt A \) là \(A \ge 0\).

Lời giải:

Điều kiện xác định của căn thức \(\sqrt {x - 1} \) là \(x - 1 \ge 0\), suy ra \(x \ge 1\).

Đáp án: B

Câu 2: Nghiệm của phương trình \(\left( {{x^2} + 3} \right)\left( {1 - x} \right) = 0\) là

A. \(x =  - 3;x = 1\).

B. \(x =  - 3;x =  - 1\).

C. \(x = 1\).

D. \(x =  - 3\).

Phương pháp:

Giải phương trình tích: \(A\left( x \right).B\left( x \right) = 0\) thì \(A\left( x \right) = 0\) hoặc \(B\left( x \right) = 0\).

Lời giải:

Ta có:

\(\left( {{x^2} + 3} \right)\left( {1 - x} \right) = 0\)

\({x^2} + 3 = 0\)                           hoặc \(1 - x = 0\).

\({x^2} =  - 3\) (không thoả mãn) hoặc \(x = 1\).

Vậy \(x = 1\).

Đáp án: C

Câu 3: Bất phương trình \(1 - 3x \le  - 4x + 3\) có bao nhiêu nghiệm là số tự nhiên?

A. 2.

B. 0.

C. 3.

D. 1.

Phương pháp:

Chuyển vế để giải bất phương trình.

Xác định các giá trị của x là số tự nhiên.

Lời giải:

Ta có:

\(\begin{array}{l}1 - 3x \le  - 4x + 3\\4x - 3x \le 3 - 1\\x \le 2\end{array}\)

Các giá trị x là số tự nhiên là: 0; 1; 2.

Vậy có 3 giá trị.

Đáp án: C

Câu 4: Phương trình nào sau đây không phải là phương trình bậc nhất hai ẩn của \(x\) và \(y\)?

A. \(x + y = 1\).

B. \({x^2} - y = 1\).

C. \(x - y = 0\).

D. \( - 2x + y - 3 = 0\).

Phương pháp:

Phương trình bậc hai một ẩn có dạng \(ax + by = c\) với \(a \ne 0\) hoặc \(b \ne 0\).

Lời giải:

Phương trình \({x^2} - y = 1\) không phải phương trình bậc nhất hai ẩn vì bậc của \(x\) là 2.

Đáp án: B

Câu 5: Hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{x - y = 3}\\{3x + y = 1}\end{array}} \right.\) có nghiệm là

A. \(\left( {x;y} \right) = \left( { - 1; - 2} \right)\).

B. \(\left( {x;y} \right) = \left( { - 1;2} \right)\).

C. \(\left( {x;y} \right) = \left( {1;2} \right)\).

D. \(\left( {x;y} \right) = \left( {1; - 2} \right)\).

Phương pháp:

Sử dụng máy tính cầm tay để bấm nghiệm.

Lời giải:

Hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{x - y = 3}\\{3x + y = 1}\end{array}} \right.\) có nghiệm là \(\left( {x;y} \right) = \left( {1; - 2} \right)\).

Đáp án: D

Câu 6: Gọi \({x_1},{x_2}\) là hai nghiệm của phương trình \({x^2} - 2025x - 2026 = 0\) khi đó \({x_1} + {x_2} + {x_1}{x_2}\) bằng

A. -1.

B. 1.

C. -4051.

D. 4051.

Phương pháp:

Chứng minh phương trình có hai nghiệm phân biệt.

Sử dụng định lí Viète để tính tổng hai nghiệm, tích hai nghiệm sau đó tính giá trị của biểu thức.

Lời giải:

Xét phương trình \({x^2} - 2025 - 2026 = 0\) có \(ac = 1.\left( { - 2026} \right) =  - 2025 < 0\) nên phương trình có hai nghiệm phân biệt.

Áp dụng định lí Viète, ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = \frac{{ - \left( { - 2025} \right)}}{1} = 2025\\{x_1}{x_2} = \frac{{ - 2026}}{1} =  - 2026\end{array} \right.\)

Vậy \({x_1} + {x_2} + {x_1}{x_2} = 2025 + \left( { - 2026} \right) =  - 1\).

Đáp án: A

Câu 7: Đồ thị hàm số \(y =  - 2{x^2}\) đi qua điểm nào trong các điểm dưới đây?

A. \(M\left( { - 2; - 8} \right)\).

B. \(N\left( {2; - 4} \right)\).

C. \(P\left( { - 2;8} \right)\).

D. \(Q\left( { - 2; - 4} \right)\).

Phương pháp:

Thay toạ độ điểm vào để kiểm tra.

Lời giải:

Thay \(x =  - 2\) vào hàm số, ta được: \(y =  - 2.{\left( { - 2} \right)^2} =  - 2.4 =  - 8\) nên \(M\left( { - 2; - 8} \right)\) thuộc đồ thị hàm số, \(P\left( { - 2;8} \right)\), \(Q\left( { - 2; - 4} \right)\) không thuộc đồ thị hàm số.

Thay \(x = 2\) vào hàm số, ta được: \(y =  - {2.2^2} =  - 2.4 =  - 8\) nên \(N\left( {2; - 4} \right)\) không thuộc đồ thị hàm số.

Đáp án: A

Câu 8: Cho tam giác \(ABC\) vuông tại \(A\) có \(AB = 3cm\), \(AC = 4cm\), \(BC = 5cm\). Khi đó \({\rm{cos}}B\) bằng

A. \(\frac{3}{4}\).

B. \(\frac{3}{5}\).

C. \(\frac{4}{5}\).

D. \(\frac{4}{3}\).

Phương pháp:

Dựa vào kiến thức về tỉ số lượng giác: cos = cạnh kề / cạnh huyền.

Lời giải:

cosB = \(\frac{{AB}}{{BC}} = \frac{3}{5}\).

Đáp án: B

Câu 9: Tại thời điểm tia nắng chiếu xuống mặt đất tạo với mặt đất một góc \({40^ \circ }\) thì chiều dài bóng cây đo được là \(25\) mét (minh họa bằng hình vẽ), giả sử cây thẳng đứng và mặt đất phẳng. Hỏi cây cao bao nhiêu mét (kết quả làm tròn đến hàng đơn vị)?

A. 30.

B. 19.

C. 21.

D. 16.

Phương pháp:

Xác định hệ thức lượng liên quan để tính chiều cao cây.

Lời giải:

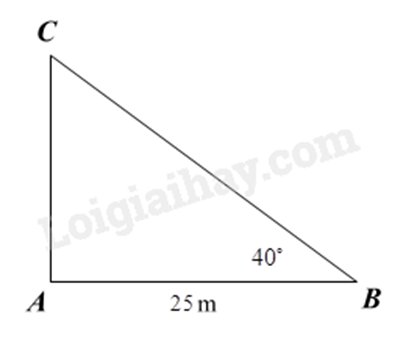
Giả sử ta có hình minh hoạ như trên, chiều cao cây là AC, bóng cây là AB, góc tạo bởi tia nắng và mặt đất là \(\widehat B = 40^\circ \).

Khi đó, chiều cao cây là: \(AC = AB.\tan B = 25.\tan 40^\circ  \approx 21\left( m \right)\)

Đáp án: C

Câu 10: Một hộp có 30 quả bóng trong đó có 10 quả bóng được sơn màu vàng và các quả bóng còn lại được sơn màu xanh (các quả bóng có kích cỡ và khối lượng như nhau). Lấy ngẫu nhiên một quả bóng trong hộp. Xác suất của biến cố “Quả bóng lấy ra được sơn màu vàng” bằng

A. \(\frac{1}{{10}}\).

B. \(\frac{2}{3}\).

C. \(\frac{1}{2}\).

D. \(\frac{1}{3}\).

Phương pháp:

Xác định số kết quả có thể.

Xác định số kết quả thuận lợi.

Xác suất của biến cố bằng tỉ số giữa số kết quả thuận lợi với số kết quả có thể.

Lời giải:

Có 30 quả bóng nên có 30 kết quả có thể khi lấy ngẫu nhiên một quả bóng trong hộp.

Có 10 quả bóng được sơn màu vàng nên có 10 kết quả thuận lợi cho biến cố “Quả bóng lấy ra được sơn màu vàng”.

Xác suất của biến cố “Quả bóng lấy ra được sơn màu vàng” là: \(\frac{{10}}{{30}} = \frac{1}{3}\).

Đáp án: D

Câu 11: Cho tam giác \(ABC\) nội tiếp đường tròn \(\left( O \right)\) và \(\widehat {ABC} = {50^ \circ }\) như hình vẽ. Số đo \(\widehat {OAC}\) bằng

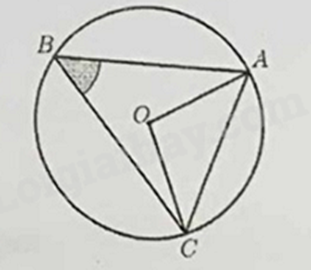
A. \({40^ \circ }\).

B. \({50^ \circ }\).

C. \({45^ \circ }\).

D. \({100^ \circ }\).

Phương pháp:

Sử dụng mối liên hệ giữa góc nội tiếp và góc ở tâm cùng chắn một cung.

Sử dụng tính chất tam giác cân.

Lời giải:

Vì \(\widehat {ABC}\) và \(\widehat {AOC}\) lần lượt là góc nội tiếp và góc ở tâm chắn cung AC

nên \(\widehat {AOC} = 2\widehat {ABC} = 2.50^\circ  = 100^\circ \).

Vì OA = OC = bán kính nên \(\Delta OAC\) cân tại O,

do đó \(\widehat {OAC} = \widehat {OCA} = \frac{{180^\circ  - \widehat {AOC}}}{2} = \frac{{180^\circ  - 100^\circ }}{2} = 40^\circ \).

Đáp án: A

Câu 12: Cho đường tròn \(\left( {O;3cm} \right)\) và đường tròn \(\left( {O{\rm{'}};5cm} \right)\) tiếp xúc ngoài với nhau. Độ dài đoạn thẳng \(OO{\rm{'}}\) bằng

A. \(2cm\).

B. \(8cm\).

C. \(6cm\).

D. \(9cm\).

Phương pháp:

Hai đường tròn tiếp xúc ngoài với nhau thì đoạn nối hai tâm = tổng bán kính hai đường tròn.

Lời giải:

Độ dài đoạn thẳng OO’ là: OO’ = 3 + 5 = 8 (cm).

Đáp án: B

PHẦN II: TỰ LUẬN

Câu 1: (1,5 điểm)

a) Giải phương trình \({x^2} + x - 6 = 0\).

b) Tính giá trị biểu thức \(A = 2\sqrt {28}  + 2\sqrt 9  - 4\sqrt 7 \).

c) Rút gọn biểu thức \(B = \left( {\frac{1}{{\sqrt a  - 3}} + \frac{2}{{\sqrt a  + 3}}} \right):\frac{{\sqrt a  - 1}}{{\sqrt a  - 3}}\) với \(a \ge 0,a \ne 1,a \ne 9\).

Phương pháp:

a) Đưa phương trình về phương trình tích rồi giải.

\(A\left( x \right).B\left( x \right) = 0\) thì \(A\left( x \right) = 0\) hoặc \(B\left( x \right) = 0\).

b) Đưa 28 ra ngoài dấu căn rồi thực hiện tính.

c) Sử dụng kết hợp các phép biến đổi với căn thức bậc hai để rút gọn.

Lời giải:

a) Ta có:

\({x^2} + x - 6 = 0\)

\({x^2} + 3x - 2x - 6 = 0\)

\(x\left( {x + 3} \right) - 2\left( {x + 3} \right) = 0\)

\(\left( {x - 2} \right)\left( {x + 3} \right) = 0\)

Để giải phương trình trên ta giải hai phương trình sau:

+) \(x - 2 = 0\) suy ra \(x = 2\)

+) \(x + 3 = 0\) suy ra \(x =  - 3\)

Vậy nghiệm của phương trình là \(x = 2\) và \(x =  - 3\).

b) Ta có:

\(A = 2\sqrt {28}  + 2\sqrt 9  - 4\sqrt 7 \)

\( = 2.2\sqrt 7  + 2.3 - 4\sqrt 7 \)

\( = 4\sqrt 7  + 6 - 4\sqrt 7 \)

\( = \left( {4\sqrt 7  - 4\sqrt 7 } \right) + 6\)

\( = 6\)

Vậy \(A = 6\).

c) \(B = \left( {\frac{1}{{\sqrt a  - 3}} + \frac{2}{{\sqrt a  + 3}}} \right):\frac{{\sqrt a  - 1}}{{\sqrt a  - 3}}\) (ĐK: \(a \ge 0,a \ne 1;a \ne 9\))

\( = \left[ {\frac{{\sqrt a  + 3}}{{\left( {\sqrt a  - 3} \right)\left( {\sqrt a  + 3} \right)}} + \frac{{2\left( {\sqrt a  - 3} \right)}}{{\left( {\sqrt a  - 3} \right)\left( {\sqrt a  + 3} \right)}}} \right]:\frac{{\sqrt a  - 3}}{{\sqrt a  - 1}}\)

\( = \frac{{\sqrt a  + 3 + 2\sqrt a  - 6}}{{\left( {\sqrt a  - 3} \right)\left( {\sqrt a  + 3} \right)}} \cdot \frac{{\sqrt a  - 3}}{{\sqrt a  - 1}}\)

\( = \frac{{3\sqrt a  - 3}}{{\left( {\sqrt a  - 3} \right)\left( {\sqrt a  + 3} \right)}} \cdot \frac{{\sqrt a  - 3}}{{\sqrt a  - 1}}\)

\( = \frac{{3\left( {\sqrt a  - 1} \right)\left( {\sqrt a  - 3} \right)}}{{\left( {\sqrt a  - 3} \right)\left( {\sqrt a  + 3} \right)\left( {\sqrt a  - 1} \right)}}\)

\( = \frac{3}{{\sqrt a  + 3}}\)

Vậy \(B = \frac{3}{{\sqrt a  + 3}}\) với \(a \ge 0,a \ne 1;a \ne 9\).

Câu 2: (2,0 điểm)

2.1.

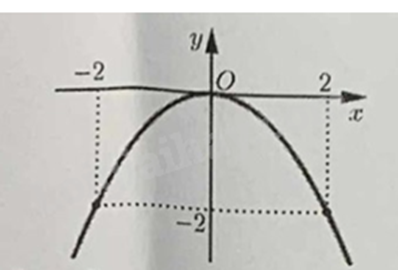
a) Cho parabol \(\left( P \right):y = \left( {m - 2} \right){x^2}\) có đồ thị như hình vẽ. Tính giá trị biểu thức \(P = 4{m^2} - 2m + 5\).

b) Cho phương trình \({x^2} - \left( {m - 1} \right)x - 3m - 6 = 0\), \(m\) là tham số. Tìm tất cả các giá trị của \(m\) để phương trình có hai nghiệm \({x_1},{x_2}\) thoả mãn điều kiện \(\left| {{x_1}} \right| = 5 + \left| {{x_2}} \right|\).

2.2. Nhân dịp khai trương, một siêu thị điện máy giảm giá mỗi tivi 20% và giảm giá mỗi máy giặt 15% so với giá niêm yết. Biết tổng số tiền bán một chiếc tivi và một chiếc máy giặt khi chưa giảm giá là 25 triệu đồng. Trong dịp này, bà Hiền đi mua một chiếc tivi và một chiếc máy giặt, bà phải trả tổng số tiền là 20,5 triệu đồng. Hỏi giá một chiếc tivi, một chiếc máy giặt khi chưa giảm giá là bao nhiêu tiền (đơn vị triệu đồng)?

Phương pháp:

2.1

a) Thay toạ độ điểm A vào hàm số để tính m.

Tính P với giá trị m vừa tìm được.

b) Chứng minh phương trình có hai nghiệm phân biệt.

Tìm hai nghiệm của phương trình bằng cách đưa phương trình về phương trình tích.

Giải phương trình \(\left| {{x_1}} \right| = 5 + \left| {{x_2}} \right|\) theo từng trường hợp.

2.2

Gọi giá một chiếc tivi, một chiếc máy giặt khi chưa giảm giá lần lượt là \(x,y\) (triệu đồng) (\(0 < x,y < 25\))

Vì giá tiền một chiếc tivi và một chiếc máy giặt khi chưa giảm giá là 25 triệu đồng nên ta có phương trình thứ nhất.

Vì giá tiền một chiếc tivi và một chiếc máy giặt sau khi giảm giá là 20,5 triệu đồng nên ta có phương trình thứ hai.

Từ hai phương trình ta lập được hệ phương trình.

Giải hệ phương trình.

Kiểm tra điều kiện và kết luận.

Lời giải:

2.1

a) Vì đồ thị hàm số đi qua \(A\left( { - 2; - 2} \right)\) nên thay \(x =  - 2;y =  - 2\) vào hàm số ta được:

\(\left( {m - 2} \right).{\left( { - 2} \right)^2} =  - 2\)

\(4\left( {m - 2} \right) =  - 2\)

\(m - 2 =  - \frac{1}{2}\)

\(m = \frac{3}{2}\)

Vậy \(P = 4{\left( {\frac{3}{2}} \right)^2} - 2 \cdot \frac{3}{2} + 5 = 4 \cdot \frac{9}{4} - 3 + 5 = 9 - 3 + 5 = 11\).

b) Xét phương trình \({x^2} - \left( {m - 1} \right)x - 3m - 6 = 0\) có:

\(\Delta  = {\left( {m - 1} \right)^2} - 4\left( { - 3m - 6} \right) = {m^2} - 2m + 1 + 12m + 24 = {m^2} + 10m + 25 = {\left( {m + 5} \right)^2} \ge 0\) với mọi \(m\).

Ta có:

\({x^2}--\left( {m - 1} \right)x - 3m - 6 = 0\)

\({x^2}--mx + x--3m - 6 = 0\)

\({x^2} + 3x--mx - 3m - 2x - 6 = 0\)

\(x\left( {x + 3} \right) - m\left( {x + 3} \right) - 2\left( {x + 3} \right) = 0\)

\(\left( {x + 3} \right)\left( {x - m - 2} \right) = 0\)

Suy ra phương trình có hai nghiệm là:

\(x = m + 2\) và \(x =  - 3\)

TH1: \({x_1} = m + 2;{x_2} =  - 3\)

Ta có: \(\left| {{x_1}} \right| = 5 + \left| {{x_2}} \right|\) nên \(\left| {m + 2} \right| = 8\)

\(m + 2 = 8\) hoặc \(m + 2 =  - 8\)

\(m = 6\) hoặc \(m =  - 10\)

TH2: \({x_1} =  - 3;{x_2} = m + 2\)

Ta có: \(3 = 5 + \left| {m + 2} \right|\) nên \(\left| {m + 2} \right| =  - 2\) (vô lí)

Vậy \(m = 6\) và \(m =  - 10\) là các giá trị cần tìm.

2.2

Gọi giá một chiếc tivi, một chiếc máy giặt khi chưa giảm giá lần lượt là \(x,y\) (triệu đồng) (\(0 < x,y < 25\))

Vì giá tiền một chiếc tivi và một chiếc máy giặt khi chưa giảm giá là 25 triệu đồng nên ta có phương trình \(x + y = 25\) (1)

Giá tiền một chiếc tivi sau khi giảm giá 20% là: \(x - 20{\rm{\% }}x = 0,8x\) (triệu đồng) Giá tiền một chiếc máy giặt sau khi giảm giá 15% là: \(y - 15{\rm{\% }}y = 0,85y\) (triệu đồng)

Vì giá tiền một chiếc tivi và một chiếc máy giặt sau khi giảm giá là 20,5 triệu đồng nên ta có phương trình \(0,8x + 0,85y = 20,5\) (2)

Từ (1) và (2) ta có hệ phương trình: \(\left\{ {\begin{array}{*{20}{l}}{x + y = 25}\\{0,8x + 0,85y = 20,5}\end{array}} \right.\)

\(\left\{ {\begin{array}{*{20}{l}}{0,8x + 0,8y = 20}\\{0,8x + 0,85y = 20,5}\end{array}} \right.\)

\(\left\{ {\begin{array}{*{20}{l}}{x + y = 25}\\{0,05y = 0,5}\end{array}} \right.\)

Vậy giá tiền một chiếc tivi trước khi giảm giá là 15 triệu đồng, giá tiền một chiếc máy giặt trước khi giảm giá là 10 triệu đồng.

Câu 3: (2,5 điểm)

Cho đường tròn \(\left( O \right)\) và dây cung \(AB\) khác đường kính. Điểm \(C\) nằm trên đường thẳng \(AB\) sao cho \(A\) nằm giữa \(B\) và \(C\). Vẽ đường kính \(DE\) của \(\left( O \right)\) vuông góc với dây cung \(AB\) tại \(K\) (\(D\) nằm trên cung lớn \(AB\)). Tia \(CD\) cắt \(\left( O \right)\) tại \(I\) (\(I\) khác \(D\)). Các dây \(AB\) và \(EI\) cắt nhau tại \(H\).

a) Chứng minh tứ giác \(DIHK\) nội tiếp đường tròn.

b) Chứng minh \(CI.CD = CH.CK\) và \(HA.IB = HB.IA\).

c) Vẽ \(DT\) vuông góc với đường thẳng \(AI\) tại \(T\), đường tròn đường kính \(CK\) cắt đoạn thẳng \(CD\) tại \(G\) (\(G\) khác \(D\)). Chứng minh \(K,G,T\) thẳng hàng.

Phương pháp:

a) Chứng minh \(\Delta DKH\) vuông tại \(K\), \(\Delta DIH\) vuông tại \(I\) nên \(D,I,H,K\) cùng thuộc đường tròn đường kính \(DH\) hay tứ giác \(DIHK\) nội tiếp đường tròn.

b) Chứng minh $\Delta CIH\backsim \Delta CKD\left( g.g \right)$ nên \(CI.CD = CH.CK\)

Chứng minh cung AE = cung \(BE\)  nên \(\angle AIE = \angle EIB\) suy ra \(IE\) là phân giác của góc \(AIB\).

Áp dụng tính chất đường phân giác trong tam giác, ta có: \(HA.IB = HB.IA\).

c) Chứng minh \(D,T,A,K\) cùng thuộc đường tròn \(DA\) nên \(\angle TKD = \angle TAD\) (cùng chắn cung \(TD\)), dẫn đến \(\angle TKD = \angle IED\) suy ra \(TK\parallel IE\) (1)

Chứng minh \(KG \bot CD\)  suy ra \(KG\parallel EI\)

Do đó \(T,G,K\) thẳng hàng.

Lời giải:

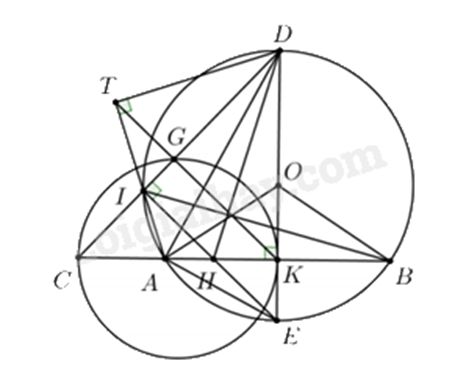
a) Do \(DE \bot AB\) tại \(K\) nên \(\Delta DKH\) vuông tại \(K\)

Suy ra \(D,K,H\) cùng thuộc đường tròn đường kính \(DH\)

Lại có \(\angle DIE = 90^\circ \) (góc nội tiếp chắn nửa đường tròn) nên \(\Delta DIH\) vuông tại \(I\)

Suy ra \(D,I,H\) cùng thuộc đường tròn đường kính \(DH\)

Vậy \(D,I,H,K\) cùng thuộc đường tròn đường kính \(DH\) hay tứ giác \(DIHK\) nội tiếp đường tròn.

b) Xét \(\Delta CIH\) và \(\Delta CKD\) có \(\angle DCK\) chung và \(\angle CIH = \angle CKD = 90^\circ \)

Suy ra $\Delta CIH\backsim \Delta CKD\left( g.g \right)$ nên \(\frac{{CI}}{{CK}} = \frac{{CH}}{{CD}}\) hay \(CI.CD = CH.CK\)

Xét \(\Delta OAB\) cân tại \(O\) có đường cao \(OK\) nên \(OK\) đồng thời là phân giác

Khi đó \(\angle AOK = \angle KOB\) suy ra cung AE = cung \(BE\)

Suy ra $\angle AIE=\frac{1}{2}sđ\overset\frown{AE}=\frac{1}{2}sđ\overset\frown{BE}=\angle EIB$

Vậy \(IE\) là phân giác của góc \(AIB\) nên \(\frac{{HA}}{{HB}} = \frac{{IA}}{{IB}}\) (tính chất đường phân giác) hay \(HA.IB = HB.IA\).

c) Do \(\Delta DTA\) vuông tại \(T\) và \(\Delta DAK\) vuông tại \(K\) nên \(D,T,A,K\) cùng thuộc đường tròn \(DA\)

Khi đó \(\angle TKD = \angle TAD\) (cùng chắn cung \(TD\))

Mà \(\angle TAD = \angle IAD = \angle IED\) (cùng chắn cung \(ID\)) nên \(\angle TKD = \angle IED\)

Suy ra \(TK\parallel IE\) (1)

Do \(G\) thuộc đường tròn đường kính \(CK\) nên \(\angle CGK = {90^ \circ }\) nên \(KG \bot CD\)

Mà \(EI \bot CD\) (do \(I\) thuộc đường tròn đường kính \(DE\)) nên \(KG\parallel EI\) (2)

Từ (1) và (2) suy ra \(T,G,K\) thẳng hàng

Câu 4: (0,5 điểm) Một cây kem ốc quế có chiều cao 18 cm, phần thân là lớp vỏ làm bằng bánh quế có dạng là một hình nón, phần đỉnh có dạng là một nửa hình cầu có bán kính bằng 3 cm bằng với bán kính của đáy hình nón (minh họa bằng hình vẽ). Tính thể tích của cả cây kem.

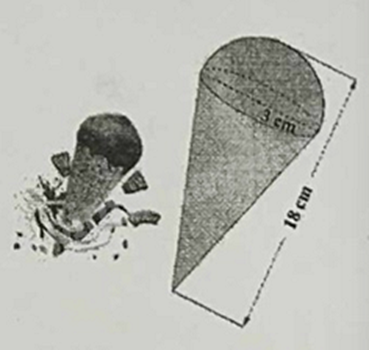
Phương pháp:

Tính chiều cao phần thân của kem ốc quế.

Tính thể tích phần thân kem hình nón: \(\frac{1}{3}\pi {r^2}h\).

Tính thể tích phần đỉnh kem nửa hình cầu: \(\frac{1}{2}.\left( {\frac{4}{3}\pi {r^3}} \right)\).

Thể tích cây kem = thể tích phần thân kem + thể tích phần đỉnh kem.

Lời giải:

Phần thân của kem ốc quế cao: \(18 - 3 = 15cm\)

Thể tích của phần thân kem là: \({V_1} = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi {.15.3^2} = 45\pi \left( {c{m^3}} \right)\)

Thể tích phần đỉnh kem là: \({V_2} = \frac{1}{2} \cdot \frac{4}{3}\pi {.3^3} = 18\pi \left( {c{m^3}} \right)\)

Thể tích cả cây kem là: \(V = 45\pi  + 18\pi  = 63\pi \left( {c{m^3}} \right)\)

Câu 5: (0,5 điểm) Giải hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{y\left( {{x^2} + x} \right) + 2 = {{\left( {{x^4} - {x^2}} \right)}^2}}\\{{x^2} + x - y = 2\sqrt {x + y} }\end{array}} \right.\)

Phương pháp:

Đặt \(a = \sqrt {x + y} \) (\(a \ge 0\))

Khi đó \({a^2} = x + y\) và \({x^2} + x - y = 2a\) (1)

Từ \({a^2} = x + y\) ta được \(y = {a^2} - x\)

Thay vào (1), đưa phương trình về phương trình tích để có hai nghiệm \(x\).

Thế từng trường hợp vào phương trình thứ nhất của hệ để tính nghiệm của hệ.
Lời giải:

Đặt \(a = \sqrt {x + y} \) (\(a \ge 0\))

Khi đó \({a^2} = x + y\) và \({x^2} + x - y = 2a\) (1)

Từ \({a^2} = x + y\) ta được \(y = {a^2} - x\)

Thay vào (1) ta được

\({x^2} + x - {a^2} + x = 2a\)

\({x^2} - {a^2} + 2x - 2a = 0\)

\(\left( {x - a} \right)\left( {x + a} \right) + 2\left( {x - a} \right) = 0\)

\(\left( {x - a} \right)\left( {x + a + 2} \right) = 0\)

Trường hợp 1: \(x = a\)

Khi đó \(x = \sqrt {x + y} \) hay \(y = {x^2} - x\) (\(x \ge 0\))

Thế vào phương trình thứ nhất của hệ ta được

\(\left( {{x^2} - x} \right)\left( {{x^2} + x} \right) + 2 = {\left( {{x^4} - {x^2}} \right)^2}\)

\(\left( {{x^4} - {x^2}} \right) + 2 = {\left( {{x^4} - {x^2}} \right)^2}\)

\({\left( {{x^4} - {x^2}} \right)^2}--\left( {{x^4} - {x^2}} \right)--2 = 0\)

\(\left( {{x^4} - {x^2} + 1} \right)\left( {{x^4} - {x^2} - 2} \right) = 0\)

\({x^4} - {x^2} - 2 = 0\) (do \({x^4} - {x^2} + 1 = {\left( {{x^2} - \frac{1}{2}} \right)^2} + \frac{3}{4} > 0,\forall x \in \mathbb{R}\))

\(\left( {{x^2} + 1} \right)\left( {{x^2} - 2} \right) = 0\) \({x^2} - 2 = 0\) (do \({x^2} + 1 > 1 > 0,\forall x \in \mathbb{R}\))

\(x = \sqrt 2 \) (do \(x > 0\))

Với \(x = \sqrt 2 \), ta được \(y = 2 - \sqrt 2 \)

Trường hợp 2: \(x + a + 2 = 0\)

\(x + \sqrt {x + y}  + 2 = 0\)

\(\sqrt {x + y}  =  - x - 2\)

Với \( - x - 2 \ge 0\) hay \(x \le  - 2\), bình phương 2 vế ta được

\(x + y = {x^2} + 4x + 4\) hay \(y = {x^2} + 3x + 4\)

Thay vào phương trình thứ nhất của hệ ta được

\(\left( {{x^2} + 3x + 4} \right)\left( {{x^2} + x} \right) + 2 = {\left( {{x^4} - {x^2}} \right)^2}\)

\({x^4} + 4{x^3} + 7{x^2} + 4x + 2 = {x^8}--2{x^6} + {x^4}\)

\({x^8} - 2{x^6} - 4{x^3} - 7{x^2} - 4x - 2 = 0\)

\({x^6}\left( {{x^2} - 2} \right) - 4x\left( {x + \frac{7}{4}} \right) - 2\left( {2x + 1} \right) = 0\) (*)

Vì \(x \le  - 2\) nên \({x^6}\left( {{x^2} - 2} \right) > 0, - 4x\left( {x + \frac{7}{4}} \right) > 0, - 2\left( {2x + 1} \right) > 0\)

Do đó VT (*) > 0

Vậy hệ phương trình có nghiệm \(\left( {x;y} \right) = \left( {\sqrt 2 ;2 - \sqrt 2 } \right)\)