Đề thi vào 10 môn Toán Cần Thơ năm 2025

Đề bài

A. PHẦN TRẮC NGHIỆM (4,0 điểm; gồm 20 câu, từ câu 1 đến câu 20).

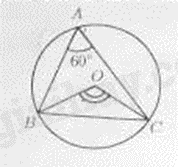
Câu 1: Cho tam giác \(ABC\) nội tiếp đường tròn \(\left( O \right)\) và \(\widehat {BAC} = {60^ \circ }\) (minh họa như hình vẽ bên dưới).

Số đo của \(\widehat {BOC}\) bằng

A. \({121^ \circ }\).

B. \({60^ \circ }\).

C. \({30^ \circ }\).

D. \({120^ \circ }\).

Câu 2: Đường cong nào trong các hình dưới đây là đồ thị của hàm số \(y = \frac{1}{2}{x^2}\)?

A.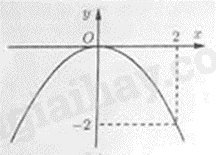 

B.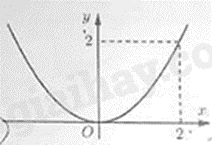 

C. 

D.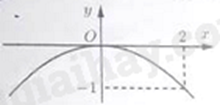 

Câu 3: Giá trị của biểu thức \(\frac{{\sqrt[3]{{81}} + 5\sqrt 2  - 3\sqrt[3]{3}}}{{\sqrt {50} }}\) bằng

A. \(1\).

B. \( - 1\).

C. \(\sqrt 3 \).

D. \( - \sqrt 3 \).

Câu 4: Cho tứ giác \(ABCD\) nội tiếp đường tròn và \(\widehat {ADC} = {110^ \circ }\) (minh họa như hình vẽ bên dưới).

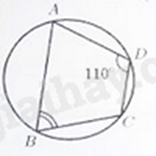
Số đo của \(\widehat {ABC}\) bằng

A. \({180^ \circ }\).

B. \({110^ \circ }\).

C. \({140^ \circ }\).

D. \({70^ \circ }\).

Câu 5: Một cổng chào được thiết kế theo hình dạng parabol là một phần của đồ thị hàm số \(y =  - \frac{1}{3}{x^2}\) (minh họa như hình vẽ bên dưới).

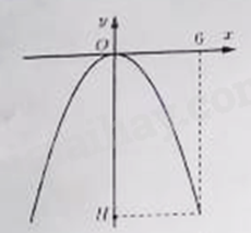
Chiều cao \(OH\) của cổng bằng

A. 48 m.

B. 3 m.

C. 12 m.

D. 4 m.

Câu 6: Chị Châm đi siêu thị mua hai loại trái cây là sầu riêng và dưa lưới. Biết giá niêm yết của 1kg sầu riêng nhiều hơn giá niêm yết của 1kg dưa lưới là 20000 đồng. Tổng số tiền chị Châm phải trả cho siêu thị khi mua 5kg sầu riêng và 3kg dưa lưới là 620000 đồng. Giá niêm yết của mỗi kilogam sầu riêng và mỗi kilogam dưa lưới lần lượt là

A. 85000 đồng và 65000 đồng.

B. 70000 đồng và 90000 đồng.

C. 65000 đồng và 85000 đồng.

D. 90000 đồng và 70000 đồng.

Câu 7: Một hộp chứa bảy tấm thẻ có cùng kích thước và khối lượng, được đánh số lần lượt là 3;4;5;6;7;8;9. Lấy ra ngẫu nhiên một tấm thẻ từ hộp. Xác suất lấy ra được tấm thẻ ghi số lớn hơn 4 bằng

A. \(\frac{2}{7}\).

B. \(\frac{5}{7}\).

C. \(\frac{3}{7}\).

D. \(\frac{4}{7}\).

Câu 8: Biết phương trình \(3{x^2} + 9x - 4 = 0\) có hai nghiệm \({x_1};{x_2}\). Giá trị của biểu thức \(2\left( {{x_1} + {x_2}} \right) + 6{x_1}{x_2}\) bằng

A. 14.

B. 2.

C. -2.

D. -14.

Câu 9: Tất cả nghiệm của phương trình \({x^2} - 10x + 9 = 0\) là

A. \({x_1} =  - 1;{x_2} =  - 9\).

B. \({x_1} = 1;{x_2} = 9\).

C. \({x_1} =  - 1;{x_2} = 9\).

D. \({x_1} = 1;{x_2} =  - 9\).

Câu 10: Góc tạo bởi tia nắng mặt trời chiếu qua điểm B trên nóc tòa nhà với mặt đất là \({39^ \circ }\) và bóng AC của tòa nhà trên mặt đất dài 27 m (minh họa như hình vẽ bên dưới).

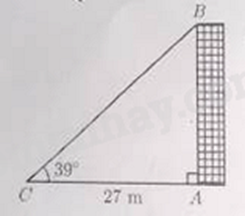
Chiều cao AB của tòa nhà (làm tròn đến hàng phần trăm) bằng

A. 21,86 m.

B. 21,87 m.

C. 33,34 m.

D. 33,35 m.

Câu 11: Nghiệm của bất phương trình \(2x - 10 > 0\) là

A. \(x < 5\).

B. \(x <  - 5\).

C. \(x > 5\).

D. \(x >  - 5\).

Câu 12: Điều kiện của \(x\) để \(\sqrt {x - 18} \) có nghĩa là

A. \(x \le 18\).

B. \(x \ge 18\).

C. \(x > 18\).

D. \(x < 18\).

Câu 13: Một hộp chứa ba quả bóng có cùng kích thước và khối lượng, trong đó có một quả bóng màu xanh, một quả bóng màu tím và một quả bóng màu vàng. Lấy ngẫu nhiên đồng thời hai quả bóng từ hộp. Các phần tử của không gian mẫu là

A. {xanh; tím}; {vàng}.

B. {xanh; tím}; {xanh; vàng}.

C. {xanh; tím}; {xanh; vàng}; {tím; vàng}.

D. {xanh; tím}; {tím; vàng}.

Câu 14: Cho bất đẳng thức \(3a + 2 \ge 3b + 2\). Khẳng định nào sau đây đúng?

A. \(a < b\).

B. \(a \ge b\).

C. \(a \le b\).

D. \(a > b\).

Câu 15: Nghiệm của hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{5x - 2y = 1}\\{x + 3y = 7}\end{array}} \right.\) là

A. \(\left( {1;2} \right)\).

B. \(\left( { - 1;2} \right)\).

C. \(\left( {1; - 2} \right)\).

D. \(\left( {2;1} \right)\).

Câu 16: Biểu đồ đoạn thẳng dưới đây biểu diễn số lượng sách giáo khoa lớp 6, lớp 7, lớp 8 và lớp 9 mà lớp 9A đã quyên góp được để tặng cho học sinh có hoàn cảnh khó khăn.

Lớp 9A quyên góp được tổng số quyển sách giáo khoa của lớp 6 và lớp 9 là

A. 130.

B. 160.

C. 180.

D. 150.

Câu 17: Cho hình trụ có đường kính của đường tròn đáy bằng 12 cm và chiều cao bằng 15 cm. Thể tích của hình trụ đã cho bằng

A. \(180\pi \) cm\(^3\).

B. \(90\pi \) cm\(^3\).

C. \(540\pi \) cm\(^3\).

D. \(2160\pi \) cm\(^3\).

Câu 18: Tập tất cả nghiệm của phương trình \(\left( {x - 6} \right)\left( {x + 4} \right) = 0\) là

A. \(x = 6;x = 4\).

B. \(x =  - 6;x = 4\).

C. \(x =  - 6;x =  - 4\).

D. \(x = 6;x =  - 4\).

Câu 19: Phương trình nào dưới đây có một nghiệm là \(x =  - 3\)?

A. \({x^2} - 4x + 3 = 0\).

B. \({x^2} + 4x + 3 = 0\).

C. \({x^2} - 2x - 3 = 0\).

D. \({x^2} + 4x - 3 = 0\).

Câu 20: Cho tam giác \(ABC\) vuông tại \(A\) có \(AB = 8\) cm, \(AC = 15\) cm. Giá trị của \({\rm{tan}}C\) bằng

A. \(\frac{8}{{15}}\).

B. \(\frac{{15}}{{17}}\).

C. \(\frac{{15}}{8}\).

D. \(\frac{{17}}{{15}}\).

B. PHẦN TỰ LUẬN (6,0 điểm; gồm 4 câu, từ câu 1 đến câu 4).

Câu 1 (1,0 điểm).

a) Giải phương trình \({x^2} - 11x + 30 = 0\).

b) Vẽ đồ thị hàm số \(y = \frac{1}{4}{x^2}\).

Câu 2 (1,5 điểm).

a) Gọi \({x_1}\), \({x_2}\) là hai nghiệm của phương trình \(2{x^2} - 6x + 1 = 0\). Tính giá trị của biểu thức:

\(M = \frac{1}{{{x_1}}} + \frac{1}{{{x_2}}} - \frac{2}{{{x_1}{x_2}}}\).

b) Chị Thơ đến một cửa hàng thời trang để mua áo và quần. Hôm ấy, cửa hàng này đã tăng giá bán một cái áo lên 10% và giảm giá bán một cái quần xuống 20% so với giá niêm yết. Do đó, chị Thơ phải trả số tiền là 1 875 000 đồng khi mua 3 cái áo và 2 cái quần. Biết rằng tổng số tiền phải trả để mua 3 cái áo và 2 cái quần theo giá niêm yết là 1 950 000 đồng. Hỏi giá tiền của một cái áo và một cái quần theo giá niêm yết là bao nhiêu?

Câu 3 (1,0 điểm).

a) Một khúc sông có bề rộng \(MN = 60\,m\). Một người dùng thuyền máy đi thẳng từ vị trí \(M\) bên này bờ sông đến vị trí \(P\) bên kia bờ sông với góc tạo bởi phương \(MP\) và phương \(MN\) là \(\widehat {NMP} = {30^ \circ }\) (như hình minh họa bên dưới). Hỏi quãng đường đi thẳng \(MN\) bao nhiêu mét (làm tròn kết quả đến hàng đơn vị của mét)?

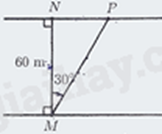
b) Trong tủ quần áo của anh An có 3 cái quần tây và 3 cái áo sơ mi. Trong đó, quần tây có 3 màu xanh, đen, trắng và áo sơ mi cũng có 3 màu xanh, đen, trắng. Anh An chọn ngẫu nhiên một bộ quần áo từ trong tủ để mặc đi dự tiệc. Tính xác suất của biến cố “Anh An chọn được một bộ quần áo cùng màu”.

Câu 4 (2,5 điểm). Cho đường tròn tâm \(O\), bán kính \(R\). Từ điểm \(P\) nằm ngoài đường tròn \(\left( O \right)\) và cách \(O\) một khoảng \(OP = 2R\), vẽ các tiếp tuyến \(PA\), \(PB\) của \(\left( O \right)\) với \(A\), \(B\) là các tiếp điểm.

a) Chứng minh 4 điểm \(O,A,P,B\) cùng nằm trên một đường tròn.

b) Kẻ đường kính \(AC\) của \(\left( O \right)\). Tia \(PC\) cắt \(\left( O \right)\) tại điểm \(E\) và cắt đường thẳng \(AB\) tại điểm \(D\). Gọi \(H\) là giao điểm của hai đường thẳng \(AB\) và \(OP\). Chứng minh đường thẳng \(OP\) vuông góc với đường thẳng \(AB\) và \(DA.DB = DC.DE\).

c) Tính diện tích tam giác \(APD\) theo \(R\).

----HẾT----

Lời giải chi tiết

I. TRẮC NGHIỆM:

Câu 1: Cho tam giác \(ABC\) nội tiếp đường tròn \(\left( O \right)\) và \(\widehat {BAC} = {60^ \circ }\) (minh họa như hình vẽ bên dưới).

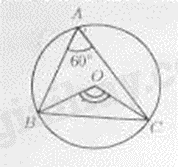
Số đo của \(\widehat {BOC}\) bằng

A. \({121^ \circ }\).

B. \({60^ \circ }\).

C. \({30^ \circ }\).

D. \({120^ \circ }\).

Phương pháp:

Số đo góc ở tâm gấp đôi số đo góc nội tiếp cùng chắn cung đó.

Lời giải:

Vì \(\widehat {BAC}\) và \(\widehat {BOC}\) lần lượt là góc nội tiếp và góc nội tiếp cùng chắn cung BC nên \(\widehat {BOC} = 2\widehat {BAC} = 2.60^\circ  = 120^\circ \).

Đáp án: D

Câu 2: Đường cong nào trong các hình dưới đây là đồ thị của hàm số \(y = \frac{1}{2}{x^2}\)?

A.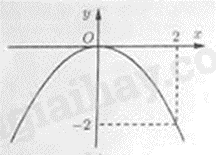 

B.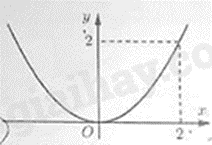 

C. 

D.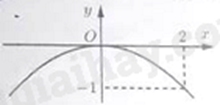 

Phương pháp:

Xác định vị trí của đồ thị so với trục hoành (nằm trên hay nằm dưới).

Xác định điểm thuộc đồ thị có thuộc hàm số \(y = \frac{1}{2}{x^2}\) hay không.

Lời giải:

Vì \(\frac{1}{2} > 0\) nên đồ thị hàm số nằm phía trên trục hoành. Ta loại đáp án A, D.

Đồ thị hình B đi qua điểm (2;2). Thay \(x = 2\) vào \(y\), ta được: \(y = \frac{1}{2}{.2^2} = 2\) nên điểm \(\left( {2;2} \right)\) thuộc đồ thị của hàm số \(y = \frac{1}{2}{x^2}\).

Vậy đồ thị hình B là đồ thị của hàm số \(y = \frac{1}{2}{x^2}\).

Đáp án: B

Câu 3: Giá trị của biểu thức \(\frac{{\sqrt[3]{{81}} + 5\sqrt 2  - 3\sqrt[3]{3}}}{{\sqrt {50} }}\) bằng

A. \(1\).

B. \( - 1\).

C. \(\sqrt 3 \).

D. \( - \sqrt 3 \).

Phương pháp:

Đối với bài tập trắc nghiệm, ta sử dụng máy tính cầm tay để tính giá trị của biểu thức.

Lời giải:

Sử dụng máy tính cầm tay, ta được: \(\frac{{\sqrt[3]{{81}} + 5\sqrt 2  - 3\sqrt[3]{3}}}{{\sqrt {50} }} = 1\)

Đáp án: A

Câu 4: Cho tứ giác \(ABCD\) nội tiếp đường tròn và \(\widehat {ADC} = {110^ \circ }\) (minh họa như hình vẽ bên dưới).

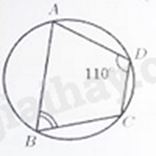
Số đo của \(\widehat {ABC}\) bằng

A. \({180^ \circ }\).

B. \({110^ \circ }\).

C. \({140^ \circ }\).

D. \({70^ \circ }\).

Phương pháp:

Trong tứ giác nội tiếp, tổng hai góc đối nhau bằng \(180^\circ \).

Lời giải:

Vì tứ giác ABCD nội tiếp đường tròn nên \(\widehat {ABC} + \widehat {ADC} = 180^\circ \).

Suy ra \(\widehat {ABC} = 180^\circ  - \widehat {ADC} = 180^\circ  - 110^\circ  = 70^\circ \).

Đáp án: D

Câu 5: Một cổng chào được thiết kế theo hình dạng parabol là một phần của đồ thị hàm số \(y =  - \frac{1}{3}{x^2}\) (minh họa như hình vẽ bên dưới).

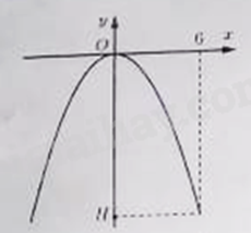
Chiều cao \(OH\) của cổng bằng

A. 48 m.

B. 3 m.

C. 12 m.

D. 4 m.

Phương pháp:

Xác định tung độ của điểm thuộc đồ thị hàm số có hoành độ là 6.

Lời giải:

Vì điểm H có tung độ trùng với tung độ của điểm có hoành độ là 6 thuộc đồ thị hàm số \(y =  - \frac{1}{3}{x^2}\) nên tung độ của điểm H là: \(y =  - \frac{1}{3}{.6^2} =  - 12\).

Do đó chiều cao OH của cổng là: \(\left| { - 12} \right| = 12\left( m \right)\)

Đáp án: C

Câu 6: Chị Châm đi siêu thị mua hai loại trái cây là sầu riêng và dưa lưới. Biết giá niêm yết của 1kg sầu riêng nhiều hơn giá niêm yết của 1kg dưa lưới là 20000 đồng. Tổng số tiền chị Châm phải trả cho siêu thị khi mua 5kg sầu riêng và 3kg dưa lưới là 620000 đồng. Giá niêm yết của mỗi kilogam sầu riêng và mỗi kilogam dưa lưới lần lượt là

A. 85000 đồng và 65000 đồng.

B. 70000 đồng và 90000 đồng.

C. 65000 đồng và 85000 đồng.

D. 90000 đồng và 70000 đồng.

Phương pháp:

Gọi giá niêm yết của mỗi kilogam sầu riêng và mỗi kilogam dưa lưới lần lượt là \(x\) và \(y\).

Lập hệ phương trình theo \(x\) và \(y\).

Giải hệ phương trình, kiểm tra điều kiện và kết luận.

Lời giải:

Gọi giá niêm yết của mỗi kilogam sầu riêng và mỗi kilogam dưa lưới lần lượt là \(x\) và \(y\) (đồng, \(x > 20000,y > 0\))

Vì giá niêm yết của 1kg sầu riêng nhiều hơn giá niêm yết của 1kg dưa lưới là 20000 đồng nên ta có phương trình: \(x - y = 20000\) (1)

Vì khi mua 5kg sầu riêng và 3kg dưa lưới hết 620000 đồng nên ta có phương trình: \(5x + 3y = 620000\) (2)

Từ (1) và (2) ta có hệ phương trình: \(\left\{ \begin{array}{l}x - y = 20000\\5x + 3y = 620000\end{array} \right.\).

Giải hệ phương trình, ta được: \(\left\{ \begin{array}{l}x = 85000\\y = 65000\end{array} \right.\) (TM).

Vậy giá niêm yết của mỗi kilogam sầu riêng và mỗi kilogam dưa lưới lần lượt là 85000 đồng và 65000 đồng.

Đáp án: A

Câu 7: Một hộp chứa bảy tấm thẻ có cùng kích thước và khối lượng, được đánh số lần lượt là 3;4;5;6;7;8;9. Lấy ra ngẫu nhiên một tấm thẻ từ hộp. Xác suất lấy ra được tấm thẻ ghi số lớn hơn 4 bằng

A. \(\frac{2}{7}\).

B. \(\frac{5}{7}\).

C. \(\frac{3}{7}\).

D. \(\frac{4}{7}\).

Phương pháp:

Xác định số kết quả có thể khi lấy ngẫu nhiên một tấm thẻ từ hộp.

Xác định số kết quả thuận lợi khi lấy được tấm thẻ ghi số lớn hơn 4.

Xác suất bằng tỉ số giữa số kết quả thuận lợi và số kết quả có thể.

Lời giải:

Có 7 kết quả có thể khi lấy ra ngẫu nhiên một tấm thẻ từ hộp, đó là: 3; 4; 5; 6; 7; 8; 9.

Có 5 kết quả thuận lợi khi lấy ra được tấm thẻ ghi số lớn hơn 4, đó là: 5; 6; 7; 8; 9.

Vậy xác suất lấy ra được tấm thẻ ghi số lớn hớn 4 là: \(\frac{5}{7}\).

Đáp án: B

Câu 8: Biết phương trình \(3{x^2} + 9x - 4 = 0\) có hai nghiệm \({x_1};{x_2}\). Giá trị của biểu thức \(2\left( {{x_1} + {x_2}} \right) + 6{x_1}{x_2}\) bằng

A. 14.

B. 2.

C. -2.

D. -14.

Phương pháp:

Chứng minh phương trình có hai nghiệm phân biệt theo a và c.

Áp dụng định lí Viète để tính \({x_1} + {x_2};{x_1}{x_2}\).

Thay vào biểu thức để tính.

Lời giải:

Xét phương trình \(3{x^2} + 9x - 4 = 0\) có \(ac = 3.\left( { - 4} \right) =  - 12 < 0\) nên phương trình có hai nghiệm phân biệt.

Áp dụng định lí Viète, ta có:

\(\left\{ \begin{array}{l}{x_1} + {x_2} =  - \frac{9}{3} =  - 3\\{x_1}{x_2} = \frac{{ - 4}}{3}\end{array} \right.\)

Thay vào biểu thức, ta được:

\(2\left( {{x_1} + {x_2}} \right) + 6{x_1}{x_2} = 2.\left( { - 3} \right) + 6.\frac{{ - 4}}{3} =  - 6 - 8 =  - 14\).

Đáp án: D

Câu 9: Tất cả nghiệm của phương trình \({x^2} - 10x + 9 = 0\) là

A. \({x_1} =  - 1;{x_2} =  - 9\).

B. \({x_1} = 1;{x_2} = 9\).

C. \({x_1} =  - 1;{x_2} = 9\).

D. \({x_1} = 1;{x_2} =  - 9\).

Phương pháp:

Tính nghiệm của phương trình bậc hai một ẩn bằng máy tính cầm tay hoặc quy tắc nhẩm nghiệm.

Lời giải:

Phương trình \({x^2} - 10x + 9 = 0\) có hai nghiệm là \({x_1} = 1;{x_2} = 9\).

Đáp án: B

Câu 10: Góc tạo bởi tia nắng mặt trời chiếu qua điểm B trên nóc tòa nhà với mặt đất là \({39^ \circ }\) và bóng AC của tòa nhà trên mặt đất dài 27 m (minh họa như hình vẽ bên dưới).

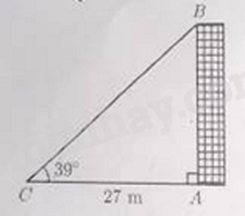
Chiều cao AB của tòa nhà (làm tròn đến hàng phần trăm) bằng

A. 21,86 m.

B. 21,87 m.

C. 33,34 m.

D. 33,35 m.

Phương pháp:

Sử dụng hệ thức lượng trong tam giác để tính AB.

Lời giải:

Áp dụng hệ thức lượng trong tam giác vào tam giác ABC, ta có chiều cao AB của toà nhà là:

\(AB = \tan C.AC = \tan 39^\circ .27 \approx 21,86\left( m \right)\)

Đáp án: A

Câu 11: Nghiệm của bất phương trình \(2x - 10 > 0\) là

A. \(x < 5\).

B. \(x <  - 5\).

C. \(x > 5\).

D. \(x >  - 5\).

Phương pháp:

Giải bất phương trình để tìm nghiệm.

Lời giải:

Ta có:

\(\begin{array}{l}2x - 10 > 0\\2x > 10\\x > 5\end{array}\)

Đáp án: C

Câu 12: Điều kiện của \(x\) để \(\sqrt {x - 18} \) có nghĩa là

A. \(x \le 18\).

B. \(x \ge 18\).

C. \(x > 18\).

D. \(x < 18\).

Phương pháp:

Đề \(\sqrt A \) có nghĩa thì \(A \ge 0\).

Lời giải:

Để \(\sqrt {x - 18} \) có nghĩa thì \(x - 18 \ge 0\), suy ra \(x \ge 18\).

Đáp án: B

Câu 13: Một hộp chứa ba quả bóng có cùng kích thước và khối lượng, trong đó có một quả bóng màu xanh, một quả bóng màu tím và một quả bóng màu vàng. Lấy ngẫu nhiên đồng thời hai quả bóng từ hộp. Các phần tử của không gian mẫu là

A. {xanh; tím}; {vàng}.

B. {xanh; tím}; {xanh; vàng}.

C. {xanh; tím}; {xanh; vàng}; {tím; vàng}.

D. {xanh; tím}; {tím; vàng}.

Phương pháp:

Xác định các kết quả có thể khi lấy ngẫu nhiên đồng thời hai quả bóng từ hộp.

Lời giải:

Các phần tử của không gian mẫu là {xanh; tím}; {xanh; vàng}; {tím; vàng}.

Đáp án: C

Câu 14: Cho bất đẳng thức \(3a + 2 \ge 3b + 2\). Khẳng định nào sau đây đúng?

A. \(a < b\).

B. \(a \ge b\).

C. \(a \le b\).

D. \(a > b\).

Phương pháp:

Sử dụng tính chất của bất đẳng thức để xác định.

Lời giải:

Ta có:

\(\begin{array}{l}3a + 2 \ge 3b + 2\\3a \ge 3b\\a \ge b\end{array}\)

Đáp án: B

Câu 15: Nghiệm của hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{5x - 2y = 1}\\{x + 3y = 7}\end{array}} \right.\) là

A. \(\left( {1;2} \right)\).

B. \(\left( { - 1;2} \right)\).

C. \(\left( {1; - 2} \right)\).

D. \(\left( {2;1} \right)\).

Phương pháp:

Đối với bài tập trắc nghiệm, sử dụng máy tính để giải nghiệm của hệ phương trình.

Lời giải:

Nghiệm của hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{5x - 2y = 1}\\{x + 3y = 7}\end{array}} \right.\) là \(\left( {x;y} \right) = \left( {1;2} \right)\).

Đáp án: A

Câu 16: Biểu đồ đoạn thẳng dưới đây biểu diễn số lượng sách giáo khoa lớp 6, lớp 7, lớp 8 và lớp 9 mà lớp 9A đã quyên góp được để tặng cho học sinh có hoàn cảnh khó khăn.

Lớp 9A quyên góp được tổng số quyển sách giáo khoa của lớp 6 và lớp 9 là

A. 130.

B. 160.

C. 180.

D. 150.

Phương pháp:

Quan sát biểu đồ, xác định số quyển sách giáo khoa lớp 6 và lớp 9.

Tính tổng số quyển sách giáo khoa của lớp 6 và lớp 9.

Lời giải:

Tổng số quyển sách giáo khoa của lớp 6 và lớp 9 mà lớp 9A quyên góp được là: \(80 + 70 = 150\) (quyển)

Đáp án: D

Câu 17: Cho hình trụ có đường kính của đường tròn đáy bằng 12 cm và chiều cao bằng 15 cm. Thể tích của hình trụ đã cho bằng

A. \(180\pi \) cm\(^3\).

B. \(90\pi \) cm\(^3\).

C. \(540\pi \) cm\(^3\).

D. \(2160\pi \) cm\(^3\).

Phương pháp:

Công thức tính thể tích hình trụ: \(V = \pi {r^2}h\).

Lời giải:

Thể tích của hình trụ đã cho là:

\(V = \pi .{\left( {\frac{{12}}{2}} \right)^2}.15 = 540\pi \left( {c{m^3}} \right)\)

Đáp án: C

Câu 18: Tập tất cả nghiệm của phương trình \(\left( {x - 6} \right)\left( {x + 4} \right) = 0\) là

A. \(x = 6;x = 4\).

B. \(x =  - 6;x = 4\).

C. \(x =  - 6;x =  - 4\).

D. \(x = 6;x =  - 4\).

Phương pháp:

Giải phương trình tích: \(\left( {ax + b} \right)\left( {cx + d} \right) = 0\) thì \(ax + b = 0\) hoặc \(cx + d = 0\).

Lời giải:

\(\left( {x - 6} \right)\left( {x + 4} \right) = 0\)

\(x - 6 = 0\) hoặc \(x + 4 = 0\)

\(x = 6\) hoặc \(x =  - 4\).

Vậy \(x = 6;x =  - 4\).

Đáp án: D

Câu 19: Phương trình nào dưới đây có một nghiệm là \(x =  - 3\)?

A. \({x^2} - 4x + 3 = 0\).

B. \({x^2} + 4x + 3 = 0\).

C. \({x^2} - 2x - 3 = 0\).

D. \({x^2} + 4x - 3 = 0\).

Phương pháp:

Thay \(x =  - 3\) vào các phương trình để kiểm tra.

Lời giải:

Ta có: \({\left( { - 3} \right)^2} + 4.\left( { - 3} \right) + 3 = 9 - 12 + 3 = 0\) nên \(x =  - 3\) là nghiệm của phương trình \({x^2} + 4x + 3 = 0\).

Đáp án: B

Câu 20: Cho tam giác \(ABC\) vuông tại \(A\) có \(AB = 8\) cm, \(AC = 15\) cm. Giá trị của \({\rm{tan}}C\) bằng

A. \(\frac{8}{{15}}\).

B. \(\frac{{15}}{{17}}\).

C. \(\frac{{15}}{8}\).

D. \(\frac{{17}}{{15}}\).

Phương pháp:

Sử dụng tỉ số lượng giác trong tam giác.

Lời giải:

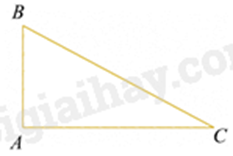
Ta có: \(\tan C = \frac{{AB}}{{AC}} = \frac{8}{{15}}\).

Đáp án: A

II. TỰ LUẬN: 

Câu 1 (1,0 điểm).

a) Giải phương trình \({x^2} - 11x + 30 = 0\).

b) Vẽ đồ thị hàm số \(y = \frac{1}{4}{x^2}\).

Phương pháp:

a) Sử dụng Delta để tính nghiệm của phương trình bậc hai một ẩn.

\(\Delta  = {b^2} - 4ac > 0\) thì phương trình có hai nghiệm phân biệt \({x_1} = \frac{{ - b + \sqrt \Delta  }}{{2a}};{x_2} = \frac{{ - b - \sqrt \Delta  }}{{2a}}\).

b) Lập bảng giá trị.

Xác định toạ độ 5 điểm thuộc đồ thị hàm số.

Vẽ đồ thị đi qua 5 điểm trên.

Lời giải:

a) Xét phương trình \({x^2} - 11x + 30 = 0\) có \(a = 1\), \(b =  - 11\), \(c = 30\).

Ta có \(\Delta  = {b^2} - 4ac = {( - 11)^2} - 4.1.30 = 1 > 0\) nên phương trình có hai nghiệm phân biệt:

\({x_1} = \frac{{ - b + \sqrt \Delta  }}{{2a}} = \frac{{11 + \sqrt 1 }}{{2.1}} = 6\);

\({x_2} = \frac{{ - b - \sqrt \Delta  }}{{2a}} = \frac{{11 - \sqrt 1 }}{{2.1}} = 5\).

Vậy phương trình \({x^2} - 11x + 30 = 0\) có hai nghiệm là \({x_1} = 6\) và \({x_2} = 5\).

b) Ta có bảng giá trị sau:

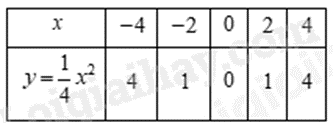
Đồ thị hàm số là đường cong parabol đi qua các điểm có tọa độ:

\(\left( { - 4;4} \right)\), \(\left( { - 2;1} \right)\); \(\left( {0;0} \right)\), \(\left( {2;1} \right)\), \(\left( {4;4} \right)\).

Hệ số \(a = \frac{1}{4} > 0\) nên parabol có bề cong hướng lên trên. Đồ thị hàm số nhận \(Oy\) làm trục đối xứng. 

Ta vẽ được đồ thị hàm số \(y = \frac{1}{4}{x^2}\) như sau:

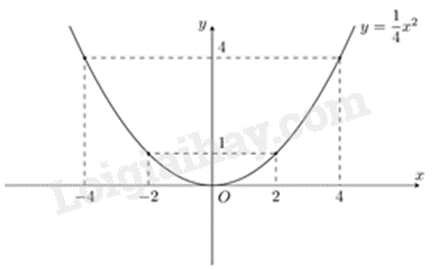
Câu 2 (1,5 điểm).

a) Gọi \({x_1}\), \({x_2}\) là hai nghiệm của phương trình \(2{x^2} - 6x + 1 = 0\). Tính giá trị của biểu thức:

\(M = \frac{1}{{{x_1}}} + \frac{1}{{{x_2}}} - \frac{2}{{{x_1}{x_2}}}\).

b) Chị Thơ đến một cửa hàng thời trang để mua áo và quần. Hôm ấy, cửa hàng này đã tăng giá bán một cái áo lên 10% và giảm giá bán một cái quần xuống 20% so với giá niêm yết. Do đó, chị Thơ phải trả số tiền là 1 875 000 đồng khi mua 3 cái áo và 2 cái quần. Biết rằng tổng số tiền phải trả để mua 3 cái áo và 2 cái quần theo giá niêm yết là 1 950 000 đồng. Hỏi giá tiền của một cái áo và một cái quần theo giá niêm yết là bao nhiêu?

Phương pháp:

a) Chứng minh phương trình có hai nghiệm phân biệt.

Áp dụng định lí Viète, biến đổi M để xuất hiện tổng, tích của hai nghiệm.

b) Gọi giá tiền của một cái áo và một cái quần theo giá niêm yết lần lượt là \(x,y\) (nghìn đồng)  \(\left( {0 < x,y < 1950} \right)\)

Vì tổng số tiền phải trả để mua 3 cái áo và 2 cái quần theo giá niêm yết là 1950000 đồng nên ta lập được phương trình thứ nhất.

Vì chị Thơ phải trả số tiền là 1875000 đồng khi mua 3 cái áo và 2 cái quần với giá bán một cái áo tăng lên 10% và giá bán một cái quần giảm xuống 20% so với giá niêm yết nên ta lập được phương trình thứ hai.

Từ hai phương trình, ta có hệ phương trình.

Giải hệ phương trình.

Kiểm tra nghiệm và kết luận.

Lời giải:

a) Xét phương trình \(2{x^2} - 6x + 1 = 0\) có 2 nghiệm phân biệt \({x_1},{x_2}\)

Áp dụng định lý Viète ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 3\\{x_1}.{x_2} = \frac{1}{2}\end{array} \right.\)

Khi đó ta có: \(M = \frac{1}{{{x_1}}} + \frac{1}{{{x_2}}} + \frac{2}{{{x_1}{x_2}}} = \frac{{{x_1} + {x_2} + 2}}{{{x_1}{x_2}}} = \frac{{3 + 2}}{{\frac{1}{2}}} = 10\)

b) Gọi giá tiền của một cái áo và một cái quần theo giá niêm yết lần lượt là \(x,y\) (nghìn đồng)  \(\left( {0 < x,y < 1950} \right)\)

Vì tổng số tiền phải trả để mua 3 cái áo và 2 cái quần theo giá niêm yết là 1950000 đồng nên ta có phương trình: \(3x + 2y = 1950\)(1)

Giá một chiếc áo sau khi tăng thêm 10% là:  \(x + 10\% x = 1,1x\)(nghìn đồng)

Giá một chiếc quần sau khi giảm đi 20% là:  \(y - 20\% y = 0,8y\)(nghìn đồng)

Vì chị Thơ phải trả số tiền là 1875000 đồng khi mua 3 cái áo và 2 cái quần nên ta có:

\(3.1,1x + 2.0,8y = 1875\) hay \(3,3x + 1,6y = 1875\)(2)

Từ (1) và (2) ta có hệ phương trình

\(\left\{ \begin{array}{l}3x + 2y = 1950\\3,3x + 1,6y = 1875\end{array} \right.\)

\(\left\{ \begin{array}{l}3,3x + 2,2y = 2145\\3,3x + 1,6y = 1875\end{array} \right.\)

\(\left\{ \begin{array}{l}3x + 2y = 1950\\0,6y = 270\end{array} \right.\)

\(\left\{ \begin{array}{l}3x = 1050\\y = 450\end{array} \right.\)

\(\left\{ \begin{array}{l}x = 350\\y = 450\end{array} \right.\)(tmđk)

Vậy giá tiền niêm yết của một cái áo là 350 nghìn đồng, giá niêm yết của một cái quần là 450 nghìn đồng.

Câu 3 (1,0 điểm).

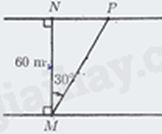
a) Một khúc sông có bề rộng \(MN = 60\,m\). Một người dùng thuyền máy đi thẳng từ vị trí \(M\) bên này bờ sông đến vị trí \(P\) bên kia bờ sông với góc tạo bởi phương \(MP\) và phương \(MN\) là \(\widehat {NMP} = {30^ \circ }\) (như hình minh họa bên dưới). Hỏi quãng đường đi thẳng \(MN\) bao nhiêu mét (làm tròn kết quả đến hàng đơn vị của mét)?

b) Trong tủ quần áo của anh An có 3 cái quần tây và 3 cái áo sơ mi. Trong đó, quần tây có 3 màu xanh, đen, trắng và áo sơ mi cũng có 3 màu xanh, đen, trắng. Anh An chọn ngẫu nhiên một bộ quần áo từ trong tủ để mặc đi dự tiệc. Tính xác suất của biến cố “Anh An chọn được một bộ quần áo cùng màu”.

Phương pháp:

a) Xác định tỉ số lượng giác liên quan đến \(\angle NMP\), MN và MP.

Từ đó tính MP dựa vào \(\angle NMP\) và MN.

Tính hiệu quãng đường MP với MN.

b) Xác định số phần tử của không gian mẫu.

Xác định số kết quả thuận lợi cho biến cố.

Xác suất bằng tỉ số giữa số kết quả thuận lợi với số phần tử của không gian mẫu.

Lời giải:

a) Xét \(\Delta MNP\) vuông tại \(N\), ta có: \(\cos NMP = \frac{{MN}}{{MP}}\)

Suy ra \(MP = \frac{{MN}}{{\cos NMP}} = \frac{{60}}{{\cos 30^\circ }} = 40\sqrt 3 \left( m \right)\).

Quãng đường MP dài hơn quãng đường MN là: \(40\sqrt 3  - 60 \approx 9\left( m \right)\).

Vậy quãng đường MP dài hơn quãng đường MN khoảng 9m.

b) Ta có bảng sau:

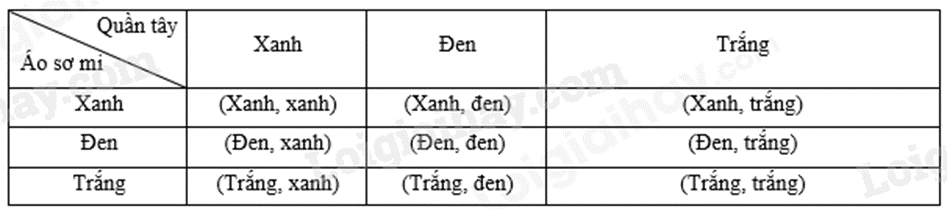
Số phần tử của không gian mẫu là 9.

Các kết quả thuận lợi cho biến cố “Anh An chọn được một bộ quần áo cùng màu” là:

(Xanh, xanh); (Đen, đen); (Trắng, trắng).

Có 3 kết quả thuận lợi cho biến cố.

Xác suất của biến cố “Anh An chọn được một bộ quần áo cùng màu” là: \(\frac{3}{9} = \frac{1}{3}\).

Câu 4 (2,5 điểm). Cho đường tròn tâm \(O\), bán kính \(R\). Từ điểm \(P\) nằm ngoài đường tròn \(\left( O \right)\) và cách \(O\) một khoảng \(OP = 2R\), vẽ các tiếp tuyến \(PA\), \(PB\) của \(\left( O \right)\) với \(A\), \(B\) là các tiếp điểm.

a) Chứng minh 4 điểm \(O,A,P,B\) cùng nằm trên một đường tròn.

b) Kẻ đường kính \(AC\) của \(\left( O \right)\). Tia \(PC\) cắt \(\left( O \right)\) tại điểm \(E\) và cắt đường thẳng \(AB\) tại điểm \(D\). Gọi \(H\) là giao điểm của hai đường thẳng \(AB\) và \(OP\). Chứng minh đường thẳng \(OP\) vuông góc với đường thẳng \(AB\) và \(DA.DB = DC.DE\).

c) Tính diện tích tam giác \(APD\) theo \(R\).

Phương pháp:

a) Chứng minh \(\Delta APO\) vuông tại \(A\), \(\Delta BPO\) vuông tại \(B\) nên \(A,\,\,P,\,\,B,\,\,O\) cùng thuộc đường tròn đường kính \(PO\).

b) Chứng minh \(P\) thuộc đường trung trực của \(AB\)

\(O\) thuộc đường trung trực của \(AB\)

Suy ra \(PO\) là đường trung trực của \(AB\)

Do đó \(PO \bot AB\) tại H

Chứng minh \(\Delta DAE\backsim \Delta DCB\,\,\left( g.g \right)\)

Suy ra \(DA.DB = DC.DE\)

c) Chứng minh \(AE \bot PC\) và \(AB \bot BC\)

Áp dụng tỉ số lượng giác, tính số đo các góc của tam giác OBC suy ra \(\Delta OBC\) đều, suy ra độ dài cạnh \(BC\)

Sử dụng định lí Pythagore tính \(AP\)

Từ $\Delta AOH\backsim \Delta POA\left( g.g \right)$, tính \(OH\) suy ra \(PH = OP - OH\)

Sử dụng định lí Pythagore tính \(AH\)

Chứng minh \(OP\parallel BC\) suy ra \(HD = 2BD\).

Suy ra \(HD\)

Tính \(AD = AH + HD\)

Tính \({S_{\Delta APD}} = {S_{\Delta APC}} - {S_{\Delta ADC}}\).

Lời giải:

a)

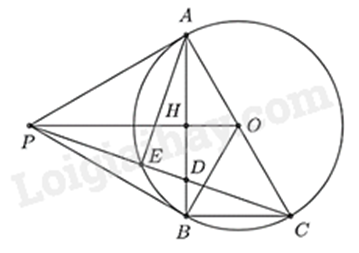
Ta có: \(\Delta APO\) vuông tại \(A\) (do \(PA\) là tiếp tuyến của \(\left( O \right)\))

Do đó \(A,\,\,P,\,\,O\) cùng thuộc đường tròn đường kính \(PO\) (1)

\(\Delta BPO\) vuông tại \(B\) (do \(PB\) là tiếp tuyến của \(\left( O \right)\))

Do đó \(B,\,\,P,\,\,O\) cùng thuộc đường tròn đường kính \(PO\) (2)

Từ (1) và (2) ta suy ra \(A,\,\,P,\,\,B,\,\,O\) cùng thuộc đường tròn đường kính \(PO\)

Vậy 4 điểm \(O,\,\,A,\,\,P,\,\,B\) cùng nằm trên một đường tròn.

b) Vì \(PA,\,\,PB\) là các tiếp tuyến của \(\left( O \right)\) nên \(PA = PB\)

Do đó \(P\) thuộc đường trung trực của \(AB\)

mà \(O\) thuộc đường trung trực của \(AB\) (do \(OA = OB\))

Suy ra \(PO\) là đường trung trực của \(AB\)

Do đó \(PO \bot AB\) tại H

Xét \(\Delta DAE\) và \(\Delta DCB\) có \(\angle ADE = \angle BDC\) (2 góc đối đỉnh)

                                           \(\angle DAE = \angle DCB\) (cùng chắn cung \(BE\))

Do đó \(\Delta DAE\backsim \Delta DCB\,\,\left( g.g \right)\)

Suy ra \(\frac{{DA}}{{DC}} = \frac{{DE}}{{DB}}\) hay \(DA.DB = DC.DE\)

c) Ta có \(\angle AEC = \angle ABC = 90^\circ \) (góc nội tiếp chắn nửa đường tròn) nên \(AE \bot PC\) và \(AB \bot BC\)

Xét \(\Delta APO\) vuông tại A có \(\cos \angle AOP = \frac{{AO}}{{PO}} = \frac{R}{{2R}} = \frac{1}{2}\) nên \(\angle AOP = 60^\circ \)

Suy ra \(\angle AOP = \angle POB = 60^\circ \).

Suy ra \(\angle COB = 180^\circ  - 60^\circ  - 60^\circ  = 60^\circ \) hay \(\Delta OBC\) đều

Suy ra \(BC = R\)

Và \(AP = \sqrt {O{P^2} - A{O^2}}  = \sqrt {4{R^2} - {R^2}}  = R\sqrt 3 \)

Ta có $\Delta AOH\backsim \Delta POA\left( g.g \right)$ nên suy ra \(O{A^2} = OH.OP\) suy ra \(OH = \frac{{O{A^2}}}{{OP}} = \frac{{{R^2}}}{{2R}} = \frac{R}{2}\) và \(PH = OP - OH = R - \frac{1}{2}R = \frac{3}{2}R\)

Suy ra \(AH = \sqrt {O{A^2} - O{H^2}}  = \sqrt {{R^2} - {{\left( {\frac{R}{2}} \right)}^2}}  = \frac{{\sqrt 3 }}{2}R\)

Ta có \(AB \bot BC;OP \bot AB\) nên \(OP\parallel BC\). Khi đó \(\frac{{BC}}{{HP}} = \frac{{BD}}{{HD}} = \frac{R}{{\frac{3}{2}R}} = \frac{2}{3}\)

Suy ra \(HD = 2BD\). Mà \(HD + BD = HB = HA = \frac{{\sqrt 3 }}{2}R\) nên \(HD = \frac{3}{5}HB = \frac{{3\sqrt 3 }}{{10}}R\)

Suy ra \(AD = AH + HD = \frac{{\sqrt 3 }}{2}R + \frac{{3\sqrt 3 }}{{10}}R = \frac{{4\sqrt 3 }}{5}R\)

Suy ra

\({S_{\Delta APD}} = {S_{\Delta APC}} - {S_{\Delta ADC}} = \frac{1}{2}AP.AC - \frac{1}{2}BC.AD = \frac{1}{2}.R\sqrt 3 .2R - \frac{1}{2}.R.\frac{{4\sqrt 3 }}{5}R = \frac{{3\sqrt 3 }}{5}{R^2}\)

Vậy \({S_{\Delta APD}} = \frac{{3\sqrt 3 }}{5}{R^2}\)