Đề thi vào 10 môn Toán Lào Cai năm 2025

Đề bài

Câu 1 (1,0 điểm). Tính giá trị các biểu thức sau:

a) \(A = \sqrt {64} \).

b) \(B = \sqrt {36}  - \sqrt 4 \).

Câu 2 (1,0 điểm). Giải phương trình: \({x^2} + 5x + 6 = 0\).

Câu 3 (1,0 điểm). Giải hệ phương trình: \(\left\{ {\begin{array}{*{20}{l}}{x - 2y = 8}\\{2x + 3y =  - 5}\end{array}} \right.\).

Câu 4 (1,0 điểm). Có chín tấm thẻ lần lượt ghi các số 1;2;3;4;5;6;7;8;9. Bạn Cường rút ngẫu nhiên một tấm thẻ từ trong hộp chứa chín tấm thẻ đó.

a) Tính số phần tử của không gian mẫu.

b) Tính xác suất của biến cố A: "Rút được tấm thẻ ghi số chẵn".

Câu 5 (1,0 điểm). Cho biểu thức \(M = \left( {\frac{{\sqrt a }}{{\sqrt a  + 1}} - \frac{{\sqrt a }}{{\sqrt a  - 1}} + \frac{{2\sqrt a  - 4}}{{a - 1}}} \right):\frac{1}{{\sqrt a  - 1}}\) với \(a \ge 0,a \ne 1\).

a) Rút gọn biểu thức \(M\).

b) Tìm các giá trị của \(a\) để \(M >  - 2\).

Câu 6 (0,5 điểm). Tổng số học sinh của hai lớp 9A và 9B là 83 học sinh. Trong đợt ủng hộ vở cho các bạn học sinh vùng lũ, mỗi học sinh lớp 9A ủng hộ 4 quyển vở, mỗi học sinh lớp 9B ủng hộ 3 quyển vở nên cả hai lớp ủng hộ được 289 quyển vở. Hỏi mỗi lớp có bao nhiêu học sinh?

Câu 7 (0,5 điểm). Cho phương trình \({x^2} - 5x + 2 = 0\) có hai nghiệm là \({x_1},{x_2}\). Không giải phương trình, hãy tính giá trị của biểu thức: \(A = \sqrt {16x_1^2 + 8{x_1}{x_2} + 5{x_2} - 2}  + 3{x_2}\).

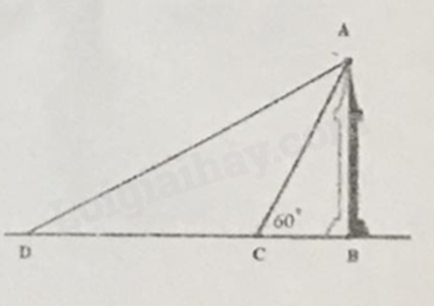
Câu 8 (1,0 điểm). Hình vẽ bên mô tả tia nắng mặt trời dọc theo \(AC\) tạo với phương nằm ngang trên mặt đất một góc \(ACB\) bằng \({60^ \circ }\). Khi đó, người ta đo được bóng của một cái tháp trên mặt đất là đoạn thẳng \(BC\) dài \(30m\). Biết tháp có phương vuông góc với mặt đất.

a) Tính chiều cao \(AB\) của tháp (làm tròn kết quả đến hàng phần trăm).

b) Tại một thời điểm khác, người ta đo được bóng của tháp có độ dài \(BD = 90m\). Tính góc \(ADB\) giữa tia nắng mặt trời và mặt đất vào thời điểm đó.

Câu 9 (1,0 điểm). Một cốc nước hình trụ có bán kính đáy phía trong thành cốc là 4 cm đang chứa nước nhưng chưa đầy. Người ta thả chìm hoàn toàn vào cốc 3 viên bi hình cầu giống hệt nhau thì thấy mực nước trong cốc dâng lên nhưng chưa đầy cốc. Biết bán kính mỗi viên bi bằng 2 cm.

a) Tính thể tích của mỗi viên bi.

b) Sau khi thả chìm hoàn toàn vào cốc 3 viên bi thì thấy chiều cao của mực nước trong cốc dâng lên so với mực nước ban đầu là \(h\) (cm). Tính \(h\).

Câu 10 (2,0 điểm). Cho tam giác \(ABC\) nhọn (\(AB < AC\)) nội tiếp đường tròn \(\left( O \right)\). Ba đường cao \(AD,BE,CF\) của tam giác \(ABC\) cắt nhau tại \(H\).

a) Chứng minh bốn điểm \(C,E,H,D\) cùng thuộc một đường tròn.

b) Kẻ đường kính \(AM\) của đường tròn \(\left( O \right)\). Chứng minh \(AD.MC = AC.BD\).

c) Gọi \(P\) là giao điểm của \(AH\) và \(EF\); \(I\) là giao điểm của \(AM\) và \(BC\); \(K\) là trung điểm của \(BC\). Chứng minh: \(K\) là trung điểm của \(HM\) và \(PI\) song song với \(HK\).

HẾT

Lời giải chi tiết

Câu 1 (1,0 điểm). Tính giá trị các biểu thức sau:

a) \(A = \sqrt {64} \).

b) \(B = \sqrt {36}  - \sqrt 4 \).

Phương pháp:

Tính căn bậc hai: \(\sqrt {{A^2}}  = \left| A \right|\).

Lời giải:

a) \(A = \sqrt {64}  = \sqrt {{8^2}}  = 8\)

b) \(B = \sqrt {36}  - \sqrt 4  = \sqrt {{6^2}}  - \sqrt {{2^2}}  = 6 - 2 = 4\)

Câu 2 (1,0 điểm). Giải phương trình: \({x^2} + 5x + 6 = 0\).

Phương pháp:

Sử dụng \(\Delta \) để tính nghiệm:

Nếu \(\Delta  > 0\) thì \({x_1} = \frac{{ - b + \sqrt \Delta  }}{{2a}};{x_2} = \frac{{ - b - \sqrt \Delta  }}{{2a}}\).

Lời giải:

Ta có: \(\Delta  = {5^2}--4.1.6 = 25--24 = 1 > 0\)

Suy ra phương trình có hai nghiệm phân biệt \({x_1} = \frac{{ - 5 + \sqrt 1 }}{{2.1}} =  - 2\) và \({x_2} = \frac{{ - 5 - \sqrt 1 }}{{2.1}} =  - 3\).

Vậy phương trình có hai nghiệm \({x_1} =  - 2\) và \({x_2} =  - 3\).

Câu 3 (1,0 điểm). Giải hệ phương trình: \(\left\{ {\begin{array}{*{20}{l}}{x - 2y = 8}\\{2x + 3y =  - 5}\end{array}} \right.\).

Phương pháp:

Sử dụng phương pháp thế để giải hệ phương trình.

Lời giải:

\(\left\{ {\begin{array}{*{20}{l}}{x - 2y = 8}\\{2x + 3y =  - 5}\end{array}} \right.\)

\(\left\{ {\begin{array}{*{20}{l}}{x = 8 + 2y}\\{2x + 3y =  - 5}\end{array}} \right.\)

\(\left\{ {\begin{array}{*{20}{l}}{x = 8 + 2y}\\{2\left( {8 + 2y} \right) + 3y =  - 5}\end{array}} \right.\)

\(\left\{ {\begin{array}{*{20}{l}}{x = 8 + 2y}\\{7y =  - 21}\end{array}} \right.\)

\(\left\{ {\begin{array}{*{20}{l}}{x = 8 + 2y}\\{y =  - 3}\end{array}} \right.\)

\(\left\{ {\begin{array}{*{20}{l}}{x = 8 + 2.\left( { - 3} \right)}\\{y =  - 3}\end{array}} \right.\)

\(\left\{ {\begin{array}{*{20}{l}}{x = 2}\\{y =  - 3}\end{array}} \right.\)

Vậy hệ phương trình có nghiệm \(\left( {x;y} \right) = \left( {2; - 3} \right)\).

Câu 4 (1,0 điểm). Có chín tấm thẻ lần lượt ghi các số 1;2;3;4;5;6;7;8;9. Bạn Cường rút ngẫu nhiên một tấm thẻ từ trong hộp chứa chín tấm thẻ đó.

a) Tính số phần tử của không gian mẫu.

b) Tính xác suất của biến cố A: "Rút được tấm thẻ ghi số chẵn".

Phương pháp:

a) Không gian mẫu là tất cả các kết quả có thể xảy ra.

b) Xác định số phần tử của không gian mẫu.

Xác định số kết quả thuận lợi cho biến cố A.

Xác suất của biến cố = số kết quả thuận lợi : số phần tử của không gian mẫu.

Lời giải:

a) Không gian mẫu của phép thử là: \(\Omega  = \left\{ {1;2;3;4;5;6;7;8;9} \right\}\) gồm 9 phần tử.

b) Có 4 kết quả thuận lợi cho biến cố A là 2; 4; 6; 8

Xác suất của biến cố A là: \(\frac{4}{9}\).

Câu 5 (1,0 điểm). Cho biểu thức \(M = \left( {\frac{{\sqrt a }}{{\sqrt a  + 1}} - \frac{{\sqrt a }}{{\sqrt a  - 1}} + \frac{{2\sqrt a  - 4}}{{a - 1}}} \right):\frac{1}{{\sqrt a  - 1}}\) với \(a \ge 0,a \ne 1\).

a) Rút gọn biểu thức \(M\).

b) Tìm các giá trị của \(a\) để \(M >  - 2\).

Phương pháp:

a) Kết hợp các phép biến đổi với căn thức bậc hai để rút gọn M.

b) Giải bất phương trình \(M >  - 2\) để tìm a.

Lời giải:

a) Với \(a \ge 0,a \ne 1\) ta có:

\(M = \left( {\frac{{\sqrt a }}{{\sqrt a  + 1}} - \frac{{\sqrt a }}{{\sqrt a  - 1}} + \frac{{2\sqrt a  - 4}}{{a - 1}}} \right):\frac{1}{{\sqrt a  - 1}}\)

\(M = \left( {\frac{{\sqrt a \left( {\sqrt a  - 1} \right)}}{{\left( {\sqrt a  + 1} \right)\left( {\sqrt a  - 1} \right)}} - \frac{{\sqrt a \left( {\sqrt a  + 1} \right)}}{{\left( {\sqrt a  + 1} \right)\left( {\sqrt a  - 1} \right)}} + \frac{{2\sqrt a  - 4}}{{\left( {\sqrt a  + 1} \right)\left( {\sqrt a  - 1} \right)}}} \right):\frac{1}{{\sqrt a  - 1}}\)

\(M = \frac{{\sqrt a \left( {\sqrt a  - 1} \right) - \sqrt a \left( {\sqrt a  + 1} \right) + 2\sqrt a  - 4}}{{\left( {\sqrt a  + 1} \right)\left( {\sqrt a  - 1} \right)}} \cdot \left( {\sqrt a  - 1} \right)\)

\(M = \frac{{a - \sqrt a  - \left( {a + \sqrt a } \right) + 2\sqrt a  - 4}}{{\sqrt a  + 1}}\)

\(M = \frac{{ - 4}}{{\sqrt a  + 1}}\)

Vậy \(M = \frac{{ - 4}}{{\sqrt a  + 1}}\) với \(a \ge 0,a \ne 1\).

b) ĐK: \(a \ge 0,a \ne 1\).

\(M >  - 2\)

\(\frac{{ - 4}}{{\sqrt a  + 1}} >  - 2\)

\(\frac{2}{{\sqrt a  + 1}} < 1\)

\(\sqrt a  + 1 > 2\)

\(\sqrt a  > 1\)

\(a > 1\)

Câu 6 (0,5 điểm). Tổng số học sinh của hai lớp 9A và 9B là 83 học sinh. Trong đợt ủng hộ vở cho các bạn học sinh vùng lũ, mỗi học sinh lớp 9A ủng hộ 4 quyển vở, mỗi học sinh lớp 9B ủng hộ 3 quyển vở nên cả hai lớp ủng hộ được 289 quyển vở. Hỏi mỗi lớp có bao nhiêu học sinh?

Phương pháp:

Gọi x, y (học sinh) lần lượt là số học sinh của lớp 9A và lớp 9B với \(x,y < 83,x,y \in \mathbb{N}\).

Vì tổng số học sinh của hai lớp 9A và 9B là 83 học sinh nên ta có phương trình thứ nhất.

Trong đợt ủng hộ vở cho các bạn học sinh vùng lũ, mỗi học sinh lớp 9A ủng hộ 4 quyển vở, mỗi học sinh lớp 9B ủng hộ 3 quyển vở nên cả hai lớp ủng hộ được 289 quyển vở, ta có phương trình thứ hai.

Từ hai phương trình ta lập được hệ phương trình.

Giải hệ phương trình.

Kiểm tra điều kiện và kết luận.

Lời giải:

Gọi x, y (học sinh) lần lượt là số học sinh của lớp 9A và lớp 9B với \(x,y < 83,x,y \in \mathbb{N}\).

Tổng số học sinh của hai lớp 9A và 9B là 83 học sinh nên ta có: \(x + y = 83\).

Trong đợt ủng hộ vở cho các bạn học sinh vùng lũ, mỗi học sinh lớp 9A ủng hộ 4 quyển vở, mỗi học sinh lớp 9B ủng hộ 3 quyển vở nên cả hai lớp ủng hộ được 289 quyển vở, nên ta có: \(4x + 3y = 289\).

Theo đề bài ta có hệ phương trình: \(\left\{ {\begin{array}{*{20}{l}}{x + y = 83}\\{4x + 3y = 289}\end{array}} \right.\)

Giải hệ phương trình ta được \(\left\{ {\begin{array}{*{20}{l}}{x = 40}\\{y = 43}\end{array}} \right.\) (tmđk)

Vậy lớp 9A có 40 học sinh, lớp 9B có 43 học sinh.

Câu 7 (0,5 điểm). Cho phương trình \({x^2} - 5x + 2 = 0\) có hai nghiệm là \({x_1},{x_2}\). Không giải phương trình, hãy tính giá trị của biểu thức: \(A = \sqrt {16x_1^2 + 8{x_1}{x_2} + 5{x_2} - 2}  + 3{x_2}\).

Phương pháp:

Áp dụng định lí Viète.

Vì \({x_2}\) là nghiệm của phương trình \({x^2} - 5x + 2 = 0\) nên ta biến đổi \(x_2^2\) theo \({x_2}\).

Thay vào biểu thức trong căn, biến đổi để xuất hiện bình phương của một tổng.

Rút gọn biểu thức A.

Lời giải:

\({x^2} - 5x + 2 = 0\) có hai nghiệm \({x_1},{x_2}\). Theo Viete, ta có \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = 5}\\{{x_1}{x_2} = 2}\end{array}} \right.\).

Suy ra hai nghiệm \({x_1} > 0,{x_2} > 0\).

Vì \({x_2}\) là nghiệm của phương trình \({x^2} - 5x + 2 = 0\), nên ta có:

\(x_2^2 - 5{x_2} + 2 = 0\) suy ra \(5{x_2} - 2 = x_2^2\).

Thay \(5{x_2} - 2 = x_2^2\) vào biểu thức trong dấu căn:

\(16x_1^2 + 8{x_1}{x_2} + 5x_2^2 - 2\)

\( = 16x_1^2 + 8{x_1}{x_2} + x_2^2\)

\( = {\left( {4{x_1}} \right)^2} + 2.\left( {4{x_1}} \right).{x_2} + {\left( {{x_2}} \right)^2}\)

\( = {\left( {4{x_1} + {x_2}} \right)^2}\)

Suy ra \(\sqrt {16x_1^2 + 8{x_1}{x_2} + 5x_2^2 - 2}  = \sqrt {{{\left( {4{x_1} + {x_2}} \right)}^2}}  = \left| {4{x_1} + {x_2}} \right|\).

Do đó biểu thức A trở thành: \(A = \left| {4{x_1} + {x_2}} \right| + 3{x_2}\).

Vì \({x_1} > 0\) và \({x_2} > 0\), nên \(4{x_1} + {x_2} > 0\).

Suy ra \(\left| {4{x_1} + {x_2}} \right| = 4{x_1} + {x_2}\).

Thay vào biểu thức A, ta được

\(A = \left( {4{x_1} + {x_2}} \right) + 3{x_2}\)

\(A = 4{x_1} + 4{x_2}\)

\(A = 4\left( {{x_1} + {x_2}} \right)\)

\(A = 4.5 = 20\)

Vậy giá trị của biểu thức A là 20.

Câu 8 (1,0 điểm). Hình vẽ bên mô tả tia nắng mặt trời dọc theo \(AC\) tạo với phương nằm ngang trên mặt đất một góc \(ACB\) bằng \({60^ \circ }\). Khi đó, người ta đo được bóng của một cái tháp trên mặt đất là đoạn thẳng \(BC\) dài \(30m\). Biết tháp có phương vuông góc với mặt đất.

a) Tính chiều cao \(AB\) của tháp (làm tròn kết quả đến hàng phần trăm).

b) Tại một thời điểm khác, người ta đo được bóng của tháp có độ dài \(BD = 90m\). Tính góc \(ADB\) giữa tia nắng mặt trời và mặt đất vào thời điểm đó.

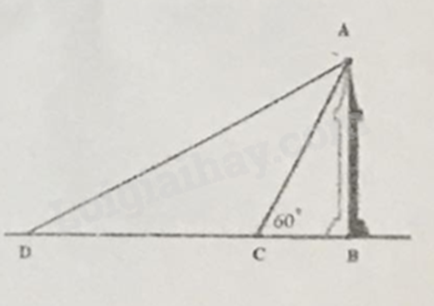
Phương pháp:

a) Áp dụng tỉ số lượng giác liên quan đến góc ACB, AB và CB.

Từ đó sử dụng hệ thức lượng để tính AB.

b) Áp dụng tỉ số lượng giác để tính góc ADB theo AB và DB.

Lời giải:

a) Xét \(\Delta ABC\) vuông tại B, áp dụng tỉ số lượng giác ta có:

\({\rm{tan}}\angle ACB = \frac{{AB}}{{CB}}\)

Suy ra: \(AB = {\rm{tan}}\angle ACB \cdot BC = {\rm{tan}}{60^ \circ } \cdot 30 = 30\sqrt 3  \approx 51,96\left( m \right)\)

b) Xét \(\Delta ABD\) vuông tại B ta có:

\({\rm{tan}}\angle ADB = \frac{{AB}}{{DB}} = \frac{{30\sqrt 3 }}{{90}} = \frac{{\sqrt 3 }}{3}\)

Suy ra \(\angle ADB = {30^ \circ }\).

Câu 9 (1,0 điểm). Một cốc nước hình trụ có bán kính đáy phía trong thành cốc là 4 cm đang chứa nước nhưng chưa đầy. Người ta thả chìm hoàn toàn vào cốc 3 viên bi hình cầu giống hệt nhau thì thấy mực nước trong cốc dâng lên nhưng chưa đầy cốc. Biết bán kính mỗi viên bi bằng 2 cm.

a) Tính thể tích của mỗi viên bi.

b) Sau khi thả chìm hoàn toàn vào cốc 3 viên bi thì thấy chiều cao của mực nước trong cốc dâng lên so với mực nước ban đầu là \(h\) (cm). Tính \(h\).

Phương pháp:

a) Áp dụng công thức tính thể tích hình cầu: \(V = \frac{4}{3}\pi {r^2}\).

b) Áp dụng công thức tính thể tích hình trụ để tính thể tích nước dâng: \(V = \pi {R^2}h\).

Thể tích nước dâng = thể tích 3 viên bi nên lập phương trình để tính h.

Lời giải:

a) Thể tích mỗi viên bi là: \({V_{bi}} = \frac{4}{3}\pi {r^3} = \frac{4}{3}\pi {.2^3} = \frac{{32\pi }}{3}\left( {c{m^3}} \right)\)

b) Thể tích nước dâng lên là: V_{nước dâng} \( = \pi {R^2}h = \pi {.4^2}h = 16\pi h\).

Vì thể tích nước tăng lên bằng thể tích 3 viên bi nên ta có:

\(16\pi h = 3 \cdot \frac{{32\pi }}{3} = 32\pi \)

Suy ra \(h = \frac{{32\pi }}{{16\pi }} = 2\left( {cm} \right)\).

Câu 10 (2,0 điểm). Cho tam giác \(ABC\) nhọn (\(AB < AC\)) nội tiếp đường tròn \(\left( O \right)\). Ba đường cao \(AD,BE,CF\) của tam giác \(ABC\) cắt nhau tại \(H\).

a) Chứng minh bốn điểm \(C,E,H,D\) cùng thuộc một đường tròn.

b) Kẻ đường kính \(AM\) của đường tròn \(\left( O \right)\). Chứng minh \(AD.MC = AC.BD\).

c) Gọi \(P\) là giao điểm của \(AH\) và \(EF\); \(I\) là giao điểm của \(AM\) và \(BC\); \(K\) là trung điểm của \(BC\). Chứng minh: \(K\) là trung điểm của \(HM\) và \(PI\) song song với \(HK\).

Phương pháp:

a) Chứng minh \(\Delta HDC\) vuông tại D, \(\Delta HEC\) vuông tại E nên H, D, C, E cùng thuộc đường tròn đường kính HC.

b) Chứng minh $\Delta ABD\backsim \Delta AMC$ (g.g) suy ra \(AD \cdot MC = AC \cdot BD\).

c) * Chứng minh \(MC||BE\), \(CF||MB\) nên BHCM là hình bình hành.

Suy ra K là trung điểm của HM.

* Chứng minh $\Delta AFP\backsim \Delta ACI$ (g.g) suy ra \(\frac{{AP}}{{AI}} = \frac{{AF}}{{AC}}\).

Chứng minh $\Delta AFH\backsim \Delta ACM$ (g.g) suy ra \(\frac{{AP}}{{AH}} = \frac{{AI}}{{AM}}\).

Suy ra PI || HM

Lời giải:

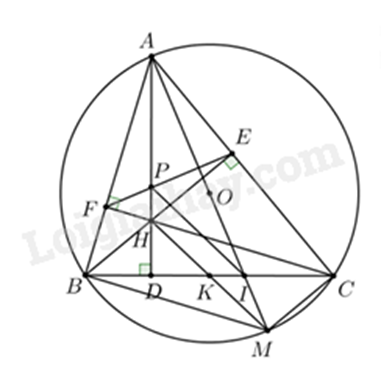
a) Ta có \(AD \bot BC\) tại D nên \(\Delta HDC\) vuông tại D. Suy ra H, D, C cùng thuộc đường tròn đường kính HC.

Tương tự \(\Delta HEC\) vuông tại E nên H, E, C cùng thuộc đường tròn đường kính HC.

Vậy H, D, C, E cùng thuộc đường tròn đường kính HC.

b) Ta có \(\angle ACM = 90^\circ \) (góc nội tiếp chắn nửa đường tròn) nên \(\angle ACM = \angle ADB\).

Lại có \(\angle ABD = \angle AMC\) (cùng chắn cung AC) nên suy ra $\Delta ABD\backsim \Delta AMC$ (g.g)

Suy ra \(\frac{{AD}}{{AC}} = \frac{{BD}}{{MC}}\) hay \(AD \cdot MC = AC \cdot BD\).

c) Do \(\angle ACM = {90^ \circ }\) nên \(MC \bot AC\). Mà \(BE \bot AC\) nên \(MC||BE\).

Tương tự \(\angle ABM = {90^ \circ }\) nên \(MB \bot AB\). Mà \(CF \bot AB\) nên \(CF||MB\).

Suy ra BHCM là hình bình hành.

Mà K là trung điểm của BC nên K là trung điểm của HM.

Do $\Delta ABD\backsim \Delta AMC$ (cmt) nên \(\angle BAD = \angle CAM\).

Kết hợp với \(\angle AFE = \angle ACB\) (cùng cộng với \(\angle BFE\) bằng \({180^ \circ }\)).

Suy ra $\Delta AFP\backsim \Delta ACI$ (g.g). Khi đó \(\frac{{AP}}{{AI}} = \frac{{AF}}{{AC}}\).

Tương tự $\Delta AFH\backsim \Delta ACM$ (g.g) nên \(\frac{{AF}}{{AC}} = \frac{{AH}}{{AM}}\).

Suy ra \(\frac{{AP}}{{AI}} = \frac{{AH}}{{AM}}\) hay \(\frac{{AP}}{{AH}} = \frac{{AI}}{{AM}}\).

Suy ra PI || HM (đpcm).