Đề tham khảo thi vào 10 môn Toán TP Hồ Chí Minh năm 2025 - Đề số 10

Đề bài

Câu 1 (1,5 điểm): Cho hàm số \(y = \frac{1}{2}{x^2}\) có đồ thị là Parabol (P).

a) Vẽ đồ thị (P) trên mặt phẳng tọa độ Oxy.

b) Tìm các điểm thuộc đồ thị có tung độ \(y = 3\;\).

Câu 2 (1 điểm): Cho phương trình bậc hai \( - {x^2} + 7x + 5 = 0\).

a) Chứng minh phương trình trên có hai nghiệm phân biệt.

b) Không giải phương trình, tính giá trị của biểu thức: \(A = {x_1}\left( {3{x_1} - {x_2}} \right) + {x_2}\left( {3{x_2} - {x_1}} \right)\).

Câu 3 (1,5 điểm): Một cửa hàng bán túi mù Pokémon 2024 với các nhân vật ngẫu nhiên bên trong. Mỗi túi chứa một Pokémon thuộc các hệ khác nhau. Trong một ngày, cửa hàng ghi nhận số lượng túi đã bán theo bảng sau:

a) Xác định cỡ mẫu, lập bảng tần số và tần số tương đối cho mẫu số liệu trên.

b) Nếu một khách hàng chọn ngẫu nhiên một túi mù, tính xác suất của mỗi biến cố sau:

A: “Túi mù được chọn thuộc hệ Điện hoặc Nước”.

B: “Túi mù được chọn không phải hệ Bí Ẩn”.

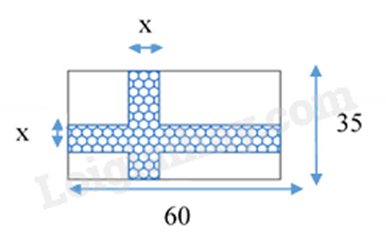
Câu 4 (1 điểm): Một mảnh vườn hình chữ nhật có chiều dài 60 m, chiều rộng 35 m. Trên mảnh vườn hình chữ nhật đó, người ta làm một lối đi có chiều rộng \(x\) (m) (\(0 < x < 10\)) như hình vẽ.

a) Viết biểu thức S biểu thị diện tích lối đi của mảnh vườn theo \(x\).

b) Tính chiều rộng lối đi, biết diện tích lối đi là \(186{m^2}\).

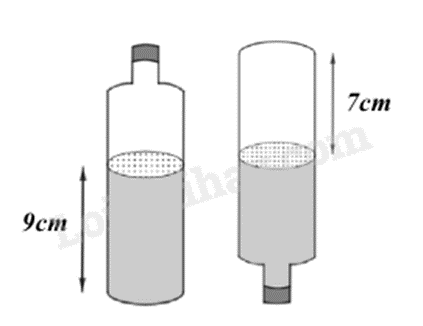
Câu 5 (1 điểm): Có một chai đựng nước suối như trong hình vẽ. Bạn An đo đường kính của đáy chai bằng 6cm, đo chiều cao của phần nước trong chai được 9cm rồi lật ngược chai và đo chiều cao của phần hình trụ không chứa nước được 7cm (hình minh họa).

a) Tính thể tích lượng nước trong chai.

b) Tính thể tích chai.

(Biết công thức thể tích hình trụ như sau:\(\;V = \pi .{R^2}.h\), kết quả làm tròn đến mililit, biết \(1c{m^3} = 1ml\), lấy \(\pi  \approx 3,14\)).

Câu 6 (1 điểm):

a) Trong một suất chiếu đặc biệt vào cuối tuần, rạp chiếu phim bán ra hai loại vé: vé dành cho học sinh, sinh viên (HSSV) và vé cho người lớn. Biết giá vé HSSV là 60 000 đồng/vé; giá vé cho người lớn là 100 000 đồng/vé. Trong suất chiếu đó, rạp đã bán tổng cộng 200 vé, thu được tổng doanh thu là 15 200 000 đồng. Tính số vé mỗi loại mà rạp chiếu phim bán được cho suất chiếu đó.

b) Biết rạp chiếu phim có sức chứa khoảng 1000 người. Với giá vé 100 000 đồng, trung bình sẽ có khoảng 300 người đến xem rạp mỗi ngày. Để tăng số lượng vé bán ra, rạp chiếu phim đã khảo sát thị trường và thấy rằng giá vé cứ giảm 5 000 đồng trên mỗi vé thì sẽ có thêm 50 người đến rạp mỗi ngày. Hỏi rạp chiếu phim phải bán ra giá vé sau khi giảm là bao nhiêu để đạt doanh thu cao nhất?

Câu 7 (3 điểm): Từ điểm A ở ngoài đường tròn (O;R), kẻ hai tiếp tuyến AB, AC đến (O), (B, C là tiếp điểm. Gọi H là giao điểm của OA và BC.

a) Chứng minh OA là đường trung trực của BC và tứ giác OBAC nội tiếp.

b) Chứng minh \(OH.OA = {R^2}\).

c) Trên đoạn AH lấy điểm D sao cho HB = HD, qua D kẻ DE vuông góc với OA (E \( \in \) AB), gọi I là trung điểm của OE, cho R = 5 cm. Tính số đo góc IHB và độ dài cạnh BE.

-------- HẾT --------

Lời giải

Câu 1 (1,5 điểm): Cho hàm số \(y = \frac{1}{2}{x^2}\) có đồ thị là Parabol (P).

a) Vẽ đồ thị (P) trên mặt phẳng tọa độ Oxy.

b) Tìm các điểm thuộc đồ thị có tung độ \(y = 3\;\).

Phương pháp

a) Lập bảng giá trị, vẽ đồ thị hàm số trên hệ trục tọa độ.

b) Thay \(y = 3\;\) vào hàm số để tìm \(x\).

Lời giải

a) Ta có bảng giá trị sau:

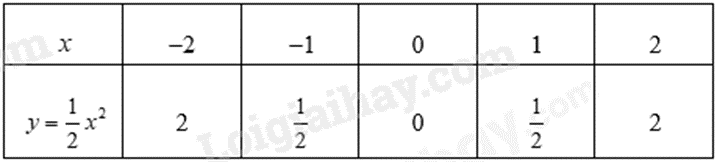
Đồ thị hàm số là đường cong parabol đi qua các điểm \(O\,\left( {0;0} \right);A\left( { - 2;2} \right);B\left( { - 1;\frac{1}{2}} \right);\,\,C\left( {1;\frac{1}{2}} \right);\,\,D\left( {2;2} \right)\).

Ta vẽ được đồ thị hàm số \(y = \frac{1}{2}{x^2}\) như sau:

b) Thay \(y = 3\;\) vào \(y = \frac{1}{2}{x^2}\), ta có: \(3 = \frac{1}{2}{x^2}\)

suy ra \({x^2} = 6\)

do đó \(x =  \pm \sqrt 6 \)

Vậy các điểm thuộc đồ thị có tung độ \(y = 3\;\) là \(\left( {\sqrt 6 ;3} \right)\) và \(\left( { - \sqrt 6 ;3} \right)\).

Câu 2 (1 điểm): Cho phương trình bậc hai \( - {x^2} + 7x + 5 = 0\).

a) Chứng minh phương trình trên có hai nghiệm phân biệt.

b) Không giải phương trình, tính giá trị của biểu thức: \(A = {x_1}\left( {3{x_1} - {x_2}} \right) + {x_2}\left( {3{x_2} - {x_1}} \right)\).

Phương pháp

a) Sử dụng \(ac < 0\) để chứng minh phương trình có hai nghiệm phân biệt.

b) Áp dụng định lí Viète và biến đổi A để xuất hiện tổng và tích của hai nghiệm.

Định lí Viète: \({x_1} + {x_2} = \frac{{ - b}}{a};{x_1}{x_2} = \frac{c}{a}\).

Lời giải

a) Phương trình \( - {x^2} + 7x + 5 = 0\) có \(ac = \left( { - 1} \right).5 =  - 5 < 0\) nên phương trình có hai nghiệm phân biệt.

b) \(A = {x_1}\left( {3{x_1} - {x_2}} \right) + {x_2}\left( {3{x_2} - {x_1}} \right)\)

Áp dụng Viète, ta có: \({x_1} + {x_2} = \frac{{ - 7}}{{ - 1}} = 7;{x_1}{x_2} = \frac{5}{{ - 1}} =  - 5\)

Ta có:
\(\begin{array}{l}A = {x_1}\left( {3{x_1} - {x_2}} \right) + {x_2}\left( {3{x_2} - {x_1}} \right)\\ = 3x_1^2 - {x_1}{x_2} + 3x_2^2 - {x_1}{x_2}\\ = 3x_1^2 + 3x_2^2 - 2{x_1}{x_2}\\ = 3x_1^2 + 6{x_1}{x_2} + 3x_2^2 - 6{x_1}{x_2} - 2{x_1}{x_2}\\ = 3\left( {x_1^2 + 2{x_1}{x_2} + x_2^2} \right) - 8{x_1}{x_2}\\ = 3{\left( {{x_1} + {x_2}} \right)^2} - 8{x_1}{x_2}\\ = {3.7^2} - 8.\left( { - 5} \right)\\ = 187\end{array}\)

Vậy \(A = 187\).

Câu 3 (1,5 điểm): Một cửa hàng bán túi mù Pokémon 2024 với các nhân vật ngẫu nhiên bên trong. Mỗi túi chứa một Pokémon thuộc các hệ khác nhau. Trong một ngày, cửa hàng ghi nhận số lượng túi đã bán theo bảng sau:

a) Xác định cỡ mẫu, lập bảng tần số và tần số tương đối cho mẫu số liệu trên.

b) Nếu một khách hàng chọn ngẫu nhiên một túi mù, tính xác suất của mỗi biến cố sau:

A: “Túi mù được chọn thuộc hệ Điện hoặc Nước”.

B: “Túi mù được chọn không phải hệ Bí Ẩn”.

Phương pháp

a) Cỡ mẫu là tổng số túi Pokémon đã bán.

Xác định các giá trị, từ đó xác định tần số là số túi đã bán.

Tần số tương đối = [(tần số.100)/cỡ mẫu] %.

b) Xác suất của biến cố bằng tỉ số giữa số kết quả thuận lợi cho biến cố với tổng số kết quả có thể (cỡ mẫu).

Số kết quả thuận lợi cho biến cố B bằng tổng số túi mù – số túi hệ Bí Ẩn.

Lời giải

a) Cỡ mẫu là tổng số túi Pokémon đã bán:

\({\rm{n}} = 25 + 18 + 22 + 15 + 20 + 12 + 8 = 120\)

Các giá trị: Điện (Pikachu); Lửa (Charmander); Nước (Squirtle); Cỏ (Bulbasaur) ; Bay (Pidgey); Rồng (Dragonite); Bí Ẩn (Mew) lần lượt có tần số, tần số tương đối là:

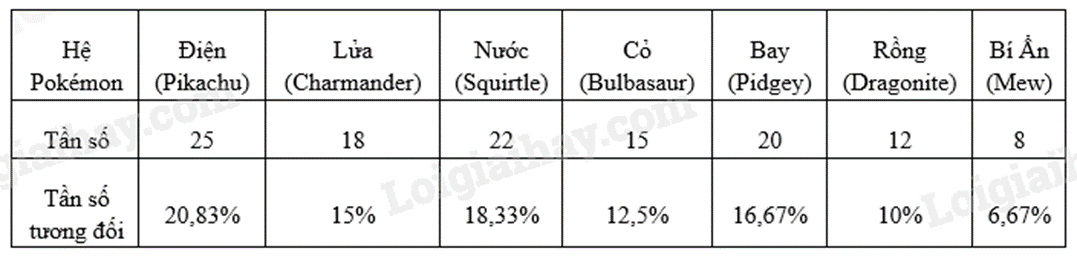
\({n_1} = 25;{n_2} = 18;{n_3} = 22;{n_4} = 15;{n_5} = 20;{n_6} = 12;{n_7} = 8\).

\({f_1} = \frac{{25.100}}{{120}}\%  \approx 20,83\% \); \({f_2} = \frac{{18.100}}{{120}}\%  = 15\% \); \({f_3} = \frac{{22.100}}{{120}} \approx 18,33\% \); \({f_4} = \frac{{15.100}}{{120}} = 12,5\% \); \({f_5} = \frac{{20.100}}{{120}} \approx 16,67\% \); \({f_6} = \frac{{12.100}}{{120}} = 10\% \); \({f_7} = \frac{{8.100}}{{120}} \approx 6,67\% \).

Bảng tần số và tần số tương đối:

b) Vì cỡ mẫu là 120 nên số kết quả có thể khi chọn ngẫu nhiên một túi mù là 120.

Xác suất của biến cố A: “Túi mù được chọn thuộc hệ Điện hoặc Nước” là:

\({\rm{P}}\left( {\rm{A}} \right) = \frac{{25 + 22}}{{120}} = \frac{{47}}{{120}}\).

Xác suất của biến cố B: “Túi mù được chọn không phải hệ Bí Ẩn” là:

\({\rm{P}}\left( {\rm{B}} \right) = \frac{{120 - 8}}{{120}} = \frac{{14}}{{15}}\).

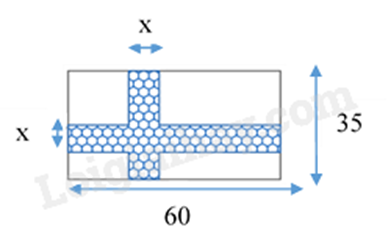
Câu 4 (1 điểm): Một mảnh vườn hình chữ nhật có chiều dài 60 m, chiều rộng 35 m. Trên mảnh vườn hình chữ nhật đó, người ta làm một lối đi có chiều rộng \(x\) (m) (\(0 < x < 10\)) như hình vẽ.

a) Viết biểu thức S biểu thị diện tích lối đi của mảnh vườn theo \(x\).

b) Tính chiều rộng lối đi, biết diện tích lối đi là \(186{m^2}\).

Phương pháp

a) Xác định diện tích phần lối đi có chiều dài 35 m, 60 m và diện tích phần chung giữa hai phần lối đi.

Biểu thức S biểu thị diện tích lối đi của mảnh vườn = tổng diện tích hai phần lối đi – phần chung của hai lối đi (do phần chung được tính 2 lần nên ta trừ 1 lần)

b) Vì diện tích lối đi là \(186{m^2}\) nên ta viết được phương trình bậc hai ẩn \(x\).

Giải phương trình để tìm \(x\).

Lời giải
a) Diện tích phần lối đi có chiều dài 35 m là: \(35x\left( {{m^2}} \right)\)

Diện tích phần lối đi có chiều dài 60 m là: \(60x\left( {{m^2}} \right)\)

Diện tích phần chung giữa hai phần lối đi là: \(x.x = {x^2}\left( {{m^2}} \right)\)

Vậy biểu thức S biểu thị diện tích lối đi của mảnh vườn theo \(x\) là: \(S = 35x + 60x - {x^2} =  - {x^2} + 95x\).

b) Vì diện tích lối đi là \(186{m^2}\) nên ta có phương trình:

\( - {x^2} + 95x = 186\) hay \( - {x^2} + 95x - 186 = 0\)

Giải phương trình ta được: \({x_1} = 93\) (không thoả mãn) và \({x_2} = 2\) (thoả mãn)

Vậy chiều rộng lối đi là 2 m.

Câu 5 (1 điểm): Có một chai đựng nước suối như trong hình vẽ. Bạn An đo đường kính của đáy chai bằng 6cm, đo chiều cao của phần nước trong chai được 9cm rồi lật ngược chai và đo chiều cao của phần hình trụ không chứa nước được 7cm (hình minh họa).

a) Tính thể tích lượng nước trong chai.

b) Tính thể tích chai.

(Biết công thức thể tích hình trụ như sau:\(\;V = \pi .{R^2}.h\), kết quả làm tròn đến mililit, biết \(1c{m^3} = 1ml\), lấy \(\pi  \approx 3,14\)).

Phương pháp

a) Tính bán kính đáy chai.

Sử dụng công thức tính thể tích hình trụ để tính thể tích nước trong chai.

b) Khi lật ngược chai, ta tính được thể tích phần còn trống trong chai bằng công thức tính thể tích hình trụ.

Thể tích chai = thể tích nước trong chai + thể tích phần còn trống.

Lời giải

a) Bán kính đáy chai là: \(\frac{6}{2} = 3\left( {cm} \right)\)

Thể tích nước trong chai là:

\({V_n} = \pi {R^2}.{h_n} \approx 3,{14.3^2}.9 = 254,34\left( {c{m^3}} \right) \approx 254\left( {ml} \right)\).

Vậy thể tích nước trong chai là khoảng 254ml.

b) Thể tích phần còn trống trong chai là:

\({V_t} = \pi {R^2}.{h_t} \approx 3,{14.3^2}.7 = 197,82\left( {c{m^3}} \right)\)

Thể tích chai là: \(V = {V_n} + {V_t} \approx 254,34 + 197,82 = 452,16\left( {c{m^3}} \right) \approx 452\left( {ml} \right)\)

Vậy thể tích chai là khoảng 452ml.

Câu 6 (1 điểm):

a) Trong một suất chiếu đặc biệt vào cuối tuần, rạp chiếu phim bán ra hai loại vé: vé dành cho học sinh, sinh viên (HSSV) và vé cho người lớn. Biết giá vé HSSV là 60 000 đồng/vé; giá vé cho người lớn là 100 000 đồng/vé. Trong suất chiếu đó, rạp đã bán tổng cộng 200 vé, thu được tổng doanh thu là 15 200 000 đồng. Tính số vé mỗi loại mà rạp chiếu phim bán được cho suất chiếu đó.

b) Biết rạp chiếu phim có sức chứa khoảng 1000 người. Với giá vé 100 000 đồng, trung bình sẽ có khoảng 300 người đến xem rạp mỗi ngày. Để tăng số lượng vé bán ra, rạp chiếu phim đã khảo sát thị trường và thấy rằng giá vé cứ giảm 5 000 đồng trên mỗi vé thì sẽ có thêm 50 người đến rạp mỗi ngày. Hỏi rạp chiếu phim phải bán ra giá vé sau khi giảm là bao nhiêu để đạt doanh thu cao nhất?

Phương pháp

a) Gọi số vé HSSV và số vé cho người lớn bán được lần lượt là \(x\) và \(y\) (vé), \(x,y \in {\mathbb{N}^*}\),\(0 < x,y < 200\).

Biểu diễn tổng số vé bán được và tổng doanh thu khi bán vé.

Từ đó lập được hệ phương trình.

Giải phương trình để tìm \(x\) và \(y\). Kiểm tra điều kiện và kết luận.

b) Gọi giá vé sau khi giảm là \(a\) (nghìn đồng), \(0 < a < 100\).

Ta tính được số tiền vé đã giảm, số người đến rạp tăng lên và số người đến rạp khi vé đã giảm.

Từ đó lập biểu thức biểu diễn doanh thu của rạp sau khi giảm giá.

Sử dụng tính chất của bất đẳng thức để tính giá trị lớn nhất của biểu thức doanh thu. Từ đó tính được giá trị của a.

Lời giải

a) Gọi số vé HSSV và số vé cho người lớn bán được lần lượt là \(x\) và \(y\) (vé), \(x,y \in {\mathbb{N}^*}\),\(0 < x,y < 200\).

Vì rạp đã bán tổng cộng 200 vé nên ta có phương trình: \(x + y = 200\). (1)

Vì giá vé HSSV là 60 000 đồng/vé; giá vé cho người lớn là 100 000 đồng/vé thì thu được tổng doanh thu là 15 200 000 đồng nên ta có phương trình: \(60\,000x + 100\,000y = 15\,200\,000\). (2)

Từ (1) và (2) ta có hệ phương trình: \(\left\{ \begin{array}{l}x + y = 200\\60\,000x + 100\,000y = 15\,200\,000\end{array} \right.\)

Giải phương trình, ta được: \(\left\{ \begin{array}{l}x = 120\\y = 80\end{array} \right.\) (thoả mãn)

Vậy số vé HSSV bán được là 120 vé, số vé cho người lớn bán được là 80 vé.

b) Gọi giá vé sau khi giảm là \(a\) (nghìn đồng), \(0 < a < 100\).

Khi đó số tiền vé đã giảm là: \(100 - a\) (nghìn đồng)

Số lần giảm 5 000 đồng là: \(\frac{{100 - a}}{5}\)

Số người đến rạp tăng lên là: \(50.\frac{{100 - a}}{5} = 10\left( {100 - a} \right) = 1000 - 10a\) (người)

Khi chưa giảm giá vé thì trung bình số người đến rạp mỗi ngày là 300 người. Số người đến rạp chiếu phim mỗi ngày sau khi giảm giá là: \(300 + 1000 - 10a = 1300 - 10a\) (người)

Doanh thu của rạp sau khi giảm giá là:

\(\begin{array}{l}a.\left( {1300 - 10a} \right) =  - 10{a^2} + 1300a\\ =  - 10\left( {{a^2} - 130a} \right) =  - 10\left( {{a^2} - 2.65a + {{65}^2} - {{65}^2}} \right)\\ =  - 10\left( {{a^2} - 2.65a + {{65}^2}} \right) - 10.\left( { - {{65}^2}} \right)\\ =  - 10{\left( {a - 65} \right)^2} + 42\,250\end{array}\)

Ta có: \({\left( {a - 65} \right)^2} \ge 0\)

nên \( - 10{\left( {a - 65} \right)^2} \le 0\)

suy ra \( - 10{\left( {a - 65} \right)^2} + 42\,250 \le 42\,250\)

Dấu “=” xảy ra là giá trị lớn nhất của \( - 10{\left( {a - 65} \right)^2} + 42\,250\).

Khi đó \(a - 65 = 0\) suy ra \(a = 65\).

Vậy rạp chiếu phim phải bán vé với giá 65 nghìn đồng để đạt doanh thu cao nhất.

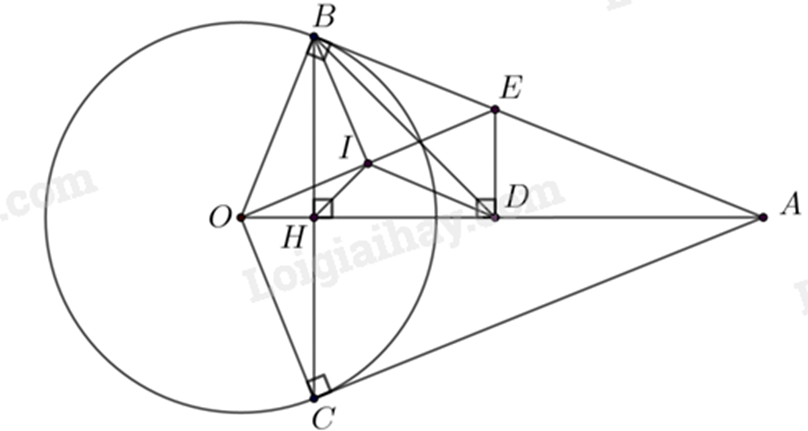
Câu 7 (3 điểm): Từ điểm A ở ngoài đường tròn (O;R), kẻ hai tiếp tuyến AB, AC đến (O), (B, C là tiếp điểm. Gọi H là giao điểm của OA và BC.

a) Chứng minh OA là đường trung trực của BC và tứ giác OBAC nội tiếp.

b) Chứng minh \(OH.OA = {R^2}\).

c) Trên đoạn AH lấy điểm D sao cho HB = HD, qua D kẻ DE vuông góc với OA (E \( \in \) AB), gọi I là trung điểm của OE, cho R = 5 cm. Tính số đo góc IHB và độ dài cạnh BE.

Phương pháp

a) Chứng minh OA là đường trung trực của BC

Chứng minh O và A cách đều B, C nên OA là đường trung trực của BC.

Chứng minh tứ giác OBAC nội tiếp

Chứng minh \(\Delta OBA\) và \(\Delta OAC\) cùng thuộc đường tròn đường kính OA nên tứ giác OBAC nội tiếp.

b) Chứng minh \(OH.OA = {R^2}\)

Chứng minh \(\Delta OHB\backsim \Delta OBA\text{ }\left( g.g \right)\) suy ra

Mà \(OB = R\) (bán kính) nên \(OH.OA = {R^2}\)

c) Tính số đo góc IHB

Chứng minh OBED nội tiếp đường tròn đường kính OE.

Chứng minh I là tâm đường tròn ngoại tiếp tứ giác OBED, suy ra IB = ID (bán kính)

Chứng minh \(\Delta IHB = \Delta IHD\left( {c.c.c} \right)\) suy ra \(\widehat {IHB} = \widehat {IHD}\)

Kết hợp \(\widehat {BHD} = 90^\circ \) suy ra \(\widehat {IHB}\).

Tính độ dài cạnh BE

Chứng minh \(\Delta BHD\) vuông cân tại H để tính \(\widehat {HDB},\widehat {BDE}\)

Từ tứ giác OBED nội tiếp đường tròn nên \(\widehat {BOE} = \widehat {BDE} = 45^\circ \) (hai góc nội tiếp cùng chắn cung BE)

Chứng minh \(\Delta BOE\) vuông cân tại B để tính BE.

Lời giải

a) Chứng minh OA là đường trung trực của BC

Ta có:

OC = OB (bán kính)

AB = AC (tính chất hai tiếp tuyến cắt nhau)

nên OA là đường trung trực của BC.

Chứng minh tứ giác OBAC nội tiếp

Xét \(\Delta OBA\) vuông tại B nên \(\Delta OBA\) nội tiếp đường tròn đường kính OA, suy ra O, B, A cùng thuộc đường tròn đường kính OA (1)

Xét \(\Delta OAC\) vuông tại C nên \(\Delta OAC\) nội tiếp đường tròn đường kính OA, suy ra O, C, A cùng thuộc đường tròn đường kính OA (2)

Từ (1) và (2) suy ra O, B, A, C cùng thuộc đường tròn đường kính OA hay tứ giác OBAC nội tiếp.

b) Chứng minh \(OH.OA = {R^2}\)

Xét \(\Delta OHB\) và \(\Delta OBA\):

\(\widehat {AOB}\) chung

\(\widehat {OHB} = \widehat {OBA} = 90^\circ \)

nên \(\Delta OHB\backsim \Delta OBA\text{ }\left( g.g \right)\)

suy ra \(\frac{{OH}}{{OB}} = \frac{{OB}}{{OA}}\), do đó

Mà \(OB = R\) (bán kính) nên \(OH.OA = {R^2}\)

c) Tính số đo góc IHB

Xét \(\Delta OBE\) vuông tại B nên \(\Delta OBE\) nội tiếp đường tròn đường kính OE, suy ra O, B, E cùng thuộc đường tròn, đường kính OE (3)

Xét \(\Delta ODE\) vuông tại D nên \(\Delta ODE\) nội tiếp đường tròn đường kính OE, suy ra O, D, E cùng thuộc đường tròn, đường kính OE (4)

Từ (3) và (4) suy ra O, B, D, E cùng thuộc đường tròn đường kính OE hay OBED nội tiếp đường tròn đường kính OE.

Mà I là trung điểm của OE (gt) nên OBED nội tiếp đường tròn tâm I, suy ra IB = ID (bán kính)

Xét \(\Delta IHB\) và \(\Delta IHD\):

IB = ID (cmt)

IH là cạnh chung

HB = HD (gt)

nên \(\Delta IHB = \Delta IHD\left( {c.c.c} \right)\)

suy ra \(\widehat {IHB} = \widehat {IHD}\)

Mà \(\widehat {BHD} = \widehat {BHA} = 90^\circ \) và \(\widehat {IHB} + \widehat {IHD} = \widehat {BHD}\) nên \(\widehat {IHB} = \widehat {IHD} = \frac{{\widehat {BHD}}}{2} = \frac{{90^\circ }}{2} = 45^\circ \).

Tính độ dài cạnh BE

Xét \(\Delta BHD\) vuông tại H có HB = HD (gt) nên \(\Delta BHD\) vuông cân tại H

Suy ra \(\widehat {HBD} = \widehat {HDB} = 45^\circ \)

Mà \(\widehat {HDB} + \widehat {BDE} = 90^\circ \) nên \(\widehat {BDE} = 90^\circ  - \widehat {HDB} = 90^\circ  - 45^\circ  = 45^\circ \)

Xét tứ giác OBED nội tiếp đường tròn tâm I nên \(\widehat {BOE} = \widehat {BDE} = 45^\circ \) (hai góc nội tiếp cùng chắn cung BE)

Xét \(\Delta BOE\) vuông tại B có \(\widehat {BOE} = 45^\circ \) nên là tam giác vuông cân tại B, do đó \(BE = BO = R = 5cm\).

Vậy \(\widehat {BHI} = 45^\circ ,BE = 5cm\).