Đề số 2 - Đề kiểm tra học kì 2 - Toán 6

Đề bài

Bài 1 (3,0 điểm) Thực hiện các phép tính (Tính hợp lý nếu có thể):

\(a)\dfrac{{ - 4}}{3} - \dfrac{7}{{ - 6}} + \dfrac{1}{2}\)       

\(b)\,\dfrac{8}{7} + \dfrac{4}{7}.\dfrac{{ - 6}}{{11}} - \dfrac{4}{7}.\dfrac{5}{{11}}\)

\(c)\,5\dfrac{3}{7} - \left( {4\dfrac{3}{7} + 1} \right)\)

\(d)1\dfrac{5}{{15}}.0,75 - \left( {\dfrac{{11}}{{20}} + 25\% } \right):\dfrac{3}{5}\)

Bài 2 (2,0 điểm) Tìm \(x\)  biết:

\(a)\,\dfrac{2}{3} + x = \dfrac{{ - 1}}{2}\)                 \(b)\,\dfrac{3}{4} - \dfrac{1}{4}:x = 1\dfrac{1}{4}\)

\(c)\,\dfrac{3}{5} - \left| {x - \dfrac{1}{2}} \right| = 25\% \)

Bài 3 (2,0 điểm) Chiều dài của mảnh vườn hình chữ nhật là \(60m\), chiều rộng bằng \(\dfrac{2}{3}\) chiều dài.

a) Tính diện tích mảnh vườn hình chữ nhật.

b) Người ta lấy một phần đất để trồng hoa. Biết \(\dfrac{3}{5}\) diện tích trồng hoa là \(240{m^2}.\) Tính diện tích trồng hoa.

c) Phần diện tích còn lại người ta trồng cây ăn quả. Hỏi diện tích hoa bằng bao nhiêu phần trăm diện tích đất trồng cây ăn quả. 

Bài 4 (2,0 điểm) Cho góc bẹt \(\angle xOy\). Trên cùng một nửa mặt phẳng bờ \(xy\) kẻ hai tia \(Oz\) và \(Ot\) sao cho \(\angle xOz = {50^0}\) và \(\angle yOt = {80^0}\).

a) Tính số đo góc \( xOt\)

b) Trong ba tia \(Ot,\,Ox\) và tia \(Oz\) tia nào nằm giữa hai tia còn lại? Vì sao?

c) Chứng tỏ rằng tia \(Oz\) là tia phân giác của góc \(xOt\). 

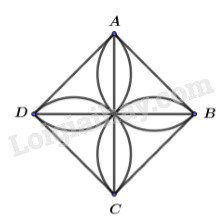
Bài 5 (1,0 điểm) Hãy sử dụng thước đo góc, thước thẳng có chia khoảng, compa, vẽ lại hình bên vào giấy kiểm tra. 

LG bài 1

Phương pháp giải:

a) Viết các phân số có mẫu số dương, rồi quy đồng mẫu số 3 phân số với MSC là 6.

b) Thực hiện theo thứ tự ưu tiên, nhân chia trước cộng trừ sau, nhóm \(\dfrac{4}{7}\) ra ngoài, rồi thực hiện phép tính theo thứ tự ưu tiên.

c) Viết hỗn số về dạng tổng của phần nguyên + phần phân số, rồi phá ngoặc, trước dấu ngoặc tròn là dấu trừ, ta đổi dấu tất cả các số hạng ở trong ngoặc, rồi sau đó thực hiện cộng trừ các số tự nhiên với nhau, phân số với nhau để việc tính toán đơn giản hơn.

Lời giải chi tiết:

\(\begin{array}{l}a)\dfrac{{ - 4}}{3} - \dfrac{7}{{ - 6}} + \dfrac{1}{2}\\ = \dfrac{{ - 4}}{3} + \dfrac{7}{6} + \dfrac{1}{2}\\ = \dfrac{{ - 8}}{6} + \dfrac{7}{6} + \dfrac{3}{6}\\ = \dfrac{{ - 8 + 7 + 3}}{6} = \dfrac{2}{6}\,\\ = \dfrac{1}{3}\end{array}\)

\(\begin{array}{l}b)\,\dfrac{8}{7} + \dfrac{4}{7}.\dfrac{{ - 6}}{{11}} - \dfrac{4}{7}.\dfrac{5}{{11}}\\ = \dfrac{8}{7} + \dfrac{4}{7}.\left( {\dfrac{{ - 6}}{{11}} - \dfrac{5}{{11}}} \right)\\ = \dfrac{8}{7} + \dfrac{4}{7}.\left( { - 1} \right)\\ = \dfrac{4}{7}\end{array}\)

\(\begin{array}{l}c)\,5\dfrac{3}{7} - \left( {4\dfrac{3}{7} + 1} \right)\\ = 5 + \dfrac{3}{7} - \left( {4 + \dfrac{3}{7} + 1} \right)\\ = 5 + \dfrac{3}{7} - 4 - \dfrac{3}{7} - 1\\ = \left( {5 - 4 - 1} \right) + \left( {\dfrac{3}{7} - \dfrac{3}{7}} \right)\\ = 0\end{array}\)

\(\begin{array}{l}d)1\dfrac{5}{{15}}.0,75 - \left( {\dfrac{{11}}{{20}} + 25\% } \right):\dfrac{3}{5}\\ = \dfrac{{20}}{{15}}.\dfrac{3}{4} - \left( {\dfrac{{11}}{{20}} + \dfrac{{25}}{{100}}} \right):\dfrac{3}{5}\\ = \dfrac{4}{3}.\dfrac{3}{4} - \left( {\dfrac{{11}}{{20}} + \dfrac{5}{{20}}} \right).\dfrac{5}{3}\\ = \,\,\,\,\,1\,\,\,\,\, - \,\,\,\,\,\,\,\,\,\,\dfrac{3}{4}.\dfrac{5}{3}\\ = \,\,\,\,\,1\,\,\,\,\, - \,\,\,\,\,\,\,\,\,\,\dfrac{5}{4}\\ = \dfrac{{ - 1}}{4}\end{array}\)

LG bài 2

Phương pháp giải:

a) Chuyển \(\dfrac{2}{3}\) từ vế trái sang vế phải ta đổi dấu thành \(\dfrac{{ - 2}}{3}\) . Thực hiện phép tính ở vế phải ta tìm được \(x\).

b) Bước 1: Giữ nguyên vế trái, ở vế phải ta chuyển hỗn số về phân số.

    Bước 2: Tìm \(\left( {\dfrac{1}{4}:x} \right)\)  ta lấy \(\dfrac{3}{4} - \dfrac{5}{4} = \dfrac{{ - 2}}{5}\) . Từ đó suy ra \(x = \dfrac{1}{4}:\dfrac{{ - 2}}{5}\) .

c) Bước 1: Viết 25% dưới dạng phân số ta được \(\dfrac{1}{4}\).

    Bước 2: Tìm \(\left| {x - \dfrac{1}{2}} \right|\) ta lấy \(\dfrac{3}{5} - \dfrac{1}{4}\) , sau đó giải tìm x, chia 2 trường hợp

Lời giải chi tiết:

\(\begin{array}{l}a)\,\dfrac{2}{3} + x = \dfrac{{ - 1}}{2}\\\,\,\,\,\,\,\,\,\,\,\,\,\,x\,\, = \dfrac{{ - 1}}{2} - \dfrac{2}{3}\\\,\,\,\,\,\,\,\,\,\,\,\,\,x = \dfrac{{ - 7}}{6}\end{array}\)

Vậy \(x =\dfrac{-7}{6}\)

\(\begin{array}{l}b)\,\dfrac{3}{4} - \dfrac{1}{4}:x = 1\dfrac{1}{4}\\\,\,\,\,\,\dfrac{3}{4} - \dfrac{1}{4}:x\, = \dfrac{5}{4}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{1}{4}:x = \dfrac{3}{4} - \dfrac{5}{4}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{1}{4}:x = \dfrac{{ - 1}}{2}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = \dfrac{1}{4}:\dfrac{{ - 1}}{2}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x\,\, = \dfrac{{ - 1}}{2}\end{array}\)

\(x =\dfrac{-1}{2}\)

\(\begin{array}{l}c)\,\dfrac{3}{5} - \left| {x - \dfrac{1}{2}} \right| = 25\% \\\,\,\,\,\,\dfrac{3}{5} - \left| {x - \dfrac{1}{2}} \right| = \dfrac{1}{4}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\left| {x - \dfrac{1}{2}} \right| = \dfrac{3}{5} - \dfrac{1}{4}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\left| {x - \dfrac{1}{2}} \right| = \dfrac{7}{{20}}\end{array}\)

TH1:

\(\begin{array}{l}\left| {x - \dfrac{1}{2}} \right| = \dfrac{7}{{20}}\\x - \dfrac{1}{2} = \dfrac{7}{{20}}\\x\,\,\,\,\,\,\,\,\,\, = \dfrac{7}{{20}} + \dfrac{1}{2}\\x\,\,\,\,\,\,\,\,\,\, = \dfrac{{17}}{{20}}\,\,\,\,\end{array}\)

TH2: 

\(\begin{array}{l}\left| {x - \dfrac{1}{2}} \right| = \dfrac{7}{{20}}\\x - \dfrac{1}{2} = \dfrac{{ - 7}}{{20}}\\x\,\,\,\,\,\,\,\,\, = \dfrac{{ - 7}}{{20}} + \dfrac{1}{2}\\x\,\,\,\,\,\,\,\,\, = \dfrac{3}{{20}}\,\,\,\end{array}\)

Vậy \(x = \dfrac{{17}}{{20}}\) , \(x = \dfrac{3}{{20}}\)

LG bài 3

Phương pháp giải:

a) Tìm chiều rộng của mảnh vườn hình chữ nhật đó, rồi tìm diện tích mảnh vườn khi đã biết chiều dài và chiều rộng. Lưu ý: Muốn tính diện tích hình chữ nhật ta lấy chiều dài nhân với chiều rộng.

b) Tìm một số biết giá trị một phân số của nó: Muốn tìm một số biết \(\dfrac{m}{n}\) của nó bằng \(a\) , ta tính \(a:\dfrac{m}{n}\,\left( {m,n \in N*} \right)\). Vậy muốn tính diện tích trồng hoa ta lấy \(240:\dfrac{3}{5}\) .

c) Tính diện tích đất trồng hoa quả = diện tích mảnh vườn – diện tích trồng hoa

Tính tỉ số diện tích đất trồng hoa so với diện tích đất trồng cây ăn quả.

Lưu ý: Muốn tính tỉ số phần trăm của hai số \(a\) và \(b\) ta nhân \(a\) với 100 rồi chia cho \(b\) và kí hiệu \(\% \) vào kết quả: \(\dfrac{{a.100}}{b}\% \)

Lời giải chi tiết:

a) Chiều rộng mảnh vườn đó là: \(\dfrac{2}{3}.60 = 40\,\left( m \right)\)

Diện tích mảnh vườn là: \(60.40 = 2400\left( {{m^2}} \right)\)

b) Diện tích đất trồng hoa là: \(240:\dfrac{3}{5} = 400\left( {{m^2}} \right)\)

c) Diện tích đất trồng hoa quả là: \(2400 - 400 = 2000\left( {{m^2}} \right)\)

Tỉ số phần trăm diện tích đất trồng hoa so với diện tích đất trồng cây ăn quả là: \(\dfrac{{400.100}}{{2000}}\%  = 20\% \)

LG bài 4

Phương pháp giải:

a) Chỉ ra tia \(Ot\) nằm giữa hai tia \(Ox\) và tia \(Oy\)

Từ đó suy ra: \(\angle xOt + \angle tOy = \angle xOy\) , thay số vào ta tìm được góc cần tính.

b) Chỉ ra \(\angle xOz < \angle xOt\) nên tia \(Oz\) nằm giữa tia \(Ox\) và tia \(Ot\)

c) Ta đã có: tia \(Oz\) nằm giữa tia \(Ox\) và tia \(Ot\) (ý b) . Chỉ ra thêm: tia \(\angle xOt = {100^0} = 2.\angle xOz\)

Lời giải chi tiết:

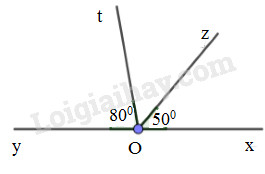
a) Vì \(\angle xOy\) là góc bẹt, nên trên nửa mặt phẳng bờ \(xy\) tia \(Ot\) nằm giữa hai tia \(Ox;\,\,Oy\)

\(\begin{array}{l} \Rightarrow \angle xOt + \angle tOy = \angle xOy\\\,\,\,\,\,\,\angle xOt + {80^0} = {180^0}\\ \Rightarrow \angle xOt = {180^0} - {80^0} = {100^0}\end{array}\)

Vậy \(\angle xOt = {100^0}\)

b) Trên nửa mặt phẳng bờ chứa tia \(Ox\) ta có:

\(\angle xOz < \angle xOt\,\left( {{{50}^0} < {{100}^0}} \right)\)

Nên tia \(Oz\) nằm giữa hai tia \(Ox\) và tia \(Ot\)

c) Vì tia Oz nằm giữa hai tia \(Ox\) và tia \(Ot\) (theo câu b)  

và \(\angle xOt = {100^0} = 2.\angle xOz\)

Nên tia \(Oz\) là tia phân giác của góc \(\angle xOt\)

LG bài 5

Phương pháp giải:

Sử dụng thước đo góc, thước thẳng có chia khoảng, compa, vẽ lại hình.

Dựng hình theo nguyên tắc: từ ngoài vào trong, từ phải qua trái. Ta dựng hình vuông trước, sau đó kẻ 2 đường chéo, sau cùng là dựng các cung tròn.

Lời giải chi tiết:

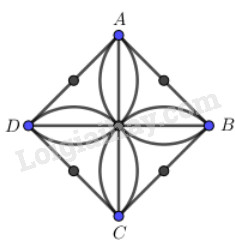
Cách dựng:

+ Dựng hình vuông ABCD cạnh \(4cm\) như hình vẽ.

+ Kẻ 2 đường chéo BD và AC.

+ Lấy các điểm M, N, P, Q lần lượt là trung điểm của các đoạn thẳng AB, BC, CD và DA.

+ Lần lượt vẽ cung tròn tâm M, N, P, Q bán kính \(2cm.\)

Ta được hình vẽ thỏa mãn đề bài.

Nguồn sưu tầm

Loigiaihay.com