Đề số 13 - Đề thi vào lớp 10 môn Toán
Đề thi vào lớp 10 môn Toán - Đề số 13 có đáp án và lời giải chi tiết
Đề bài
Câu 1 (4 điểm) Rút gọn biểu thức:
a) \(A = \sqrt {45} + \sqrt {20} - 2\sqrt 5 .\)
b) \(B = \dfrac{{a + 2\sqrt a }}{{\sqrt a + 2}} - \dfrac{{a - 4}}{{\sqrt a - 2}}\) (với \(a \ge 0,\;\;a \ne 4\)).
Câu 2 (4 điểm)
a) Giải hệ phương trình \(\left\{ \begin{array}{l}x - y = 4\\2x - y = 5\end{array} \right..\)
b) Cho hàm số \(y = \dfrac{1}{2}{x^2}\) có đồ thị \(\left( P \right)\) và đường thẳng \(d:\;y = x - 2m.\) Vẽ đồ thị \(\left( P \right).\) Tìm tất cả các giá trị của \(m\) sao cho \(d\) cắt \(\left( P \right)\) tại điểm có hoành độ bằng \( - 1.\)
Câu 3 (6 điểm) Cho phương trình \({x^2} + 4x + m + 1 = 0\,\,\,(1)\) (với m là tham số).
a) Giải phương trình (1) với m = 2.
b) Tìm điều kiện của m để phương trình (1) có nghiệm.
c) Tìm tất cả các giá trị của m sao cho phương trình (1) có hai nghiệm \({x_1};{x_2}\) thỏa mãn điều kiện \(\dfrac{{{x_1} - 1}}{{2{x_2}}} - \dfrac{{{x_2} - 1}}{{2{x_1}}} = - 3\).
Câu 4: Cho nửa đường tròn tâm O đường kính AB. Vẽ bán kính CO vuông góc với AB, M là một điểm bất kỳ trên cung AC (M khác A, C và điểm chính giữa AC), BM cắt AC tại H. Gọi K là chân đường vuông góc kẻ từ H đến AB.
a) Chứng minh tứ giác BCHK là tứ giác nội tiếp
b) Chứng minh CA là phân giác của góc MCK
c) Kẻ CP vuông góc với BM \(\left( {P \in BM} \right)\) và trên đoạn thẳng BM lấy điểm E sao cho BE = AM. Chứng minh ME = 2CP
Lời giải chi tiết
Câu 1:
\(\begin{array}{l}a)\;\;A = \sqrt {45} + \sqrt {20} - 2\sqrt 5 \\\;\;\;\;\;\;\;\; = \sqrt {{3^2}.5} + \sqrt {{2^2}.5} - 2\sqrt 5 \\\;\;\;\;\;\;\;\; = 3\sqrt 5 + 2\sqrt 5 - 2\sqrt 5 \\\;\;\;\;\;\;\;\; = 3\sqrt 5 .\\b)\;\;B = \dfrac{{a + 2\sqrt a }}{{\sqrt a + 2}} - \dfrac{{a - 4}}{{\sqrt a - 2}}\;\;\;\left( {a \ge 0,\;\;a \ne 4} \right)\\\;\;\;\;\;\;\;\, = \dfrac{{\sqrt a \left( {\sqrt a + 2} \right)}}{{\sqrt a + 2}} - \dfrac{{\left( {\sqrt a + 2} \right)\left( {\sqrt a - 2} \right)}}{{\sqrt a - 2}}\\\;\;\;\;\;\;\;\; = \sqrt a - \left( {\sqrt a + 2} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\, = \sqrt a - \sqrt a - 2\\\;\;\;\;\;\;\;\; = - 2\end{array}\)
Câu 2:
a) Giải hệ phương trình \(\left\{ \begin{array}{l}x - y = 4\\2x - y = 5\end{array} \right..\)
\(\left\{ \begin{array}{l}x - y = 4\\2x - y = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = x - 4\end{array} \right.\)\(\, \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = - 3\end{array} \right..\)
Vậy hệ phương trình có nghiệm duy nhất: \(\left( {x;\;y} \right) = \left( {1; - 3} \right).\)
b) Cho hàm số \(y = \dfrac{1}{2}{x^2}\) có đồ thị \(\left( P \right)\) và đường thẳng \(d:\;y = x - 2m.\) Vẽ đồ thị \(\left( P \right).\) Tìm tất cả các giá trị của \(m\) sao cho \(d\) cắt \(\left( P \right)\) tại điểm có hoành độ bằng \( - 1.\)
Ta có bảng giá trị:
|
\(x\) |
\( - 2\) |
\( - 1\) |
\(0\) |
\(1\) |
\(2\) |
|
\(y = \dfrac{1}{2}{x^2}\) |
\(2\) |
\(\dfrac{1}{2}\) |
\(0\) |
\(\dfrac{1}{2}\) |
\(2\) |
\( \Rightarrow \) Đồ thị hàm số \(y = \dfrac{1}{2}{x^2}\) đi qua các điểm \(\left( { - 2;2} \right);\,\,\left( { - 1;\dfrac{1}{2}} \right);\,\,\left( {0;0} \right);\,\,\left( {1;\dfrac{1}{2}} \right);\)\(\,\,\left( {2;2} \right)\)
Đồ thị:
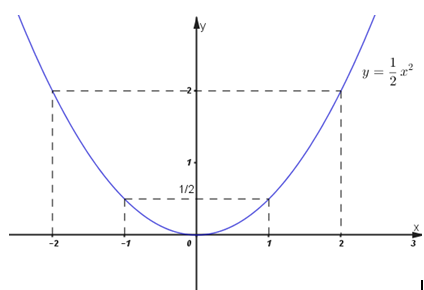
Hoành độ giao điểm của đường thẳng \(d\) và parabol \(\left( P \right)\) là nghiệm của phương trình \(\dfrac{1}{2}{x^2} = x - 2m \Leftrightarrow \dfrac{1}{2}{x^2} - x + 2m = 0.\;\;\;\left( 1 \right)\)
Để \(d\) cắt \(\left( P \right)\) tại điểm có hoành độ bằng \( - 1 \Leftrightarrow x = - 1\) là nghiệm của phương trình \(\left( 1 \right)\)
\(\begin{array}{l} \Leftrightarrow \dfrac{1}{2}{\left( { - 1} \right)^2} - \left( { - 1} \right) + 2m = 0\\ \Leftrightarrow 2m = - \dfrac{3}{2}\\ \Leftrightarrow m = - \dfrac{3}{4}.\end{array}\)
Vậy \(m = - \dfrac{3}{4}.\)
Câu 3.
a) Giải phương trình (1) với m = 2.
Thay \(m = 2\) vào \((1)\): \({x^2} + 4x + 2 + 1 = 0 \)
\(\Leftrightarrow {x^2} + 4x + 3 = 0\)
Ta có : \(a - b + c = 1 - 4 + 3 = 0\)
\( \Rightarrow \) Phương trình có hai nghiệm \(\left\{ \begin{array}{l}{x_1} = - 1\\{x_2} = - 3\end{array} \right.\)
Vậy, với \(m = 2\) thì phương trình có hai nghiệm \({x_1} = - 1,\,\,{x_2} = - 3\).
b) Tìm điều kiện của m để phương trình (1) có nghiệm.
\(\Delta ' = {2^2} - (m + 1) = 4 - m - 1 \)\(\,= 3 - m\)
Để phương trình (1) có nghiệm thì \(\Delta ' \ge 0 \Leftrightarrow 3 - m \ge 0 \Leftrightarrow m \le 3\).
c) Tìm tất cả các giá trị của m sao cho phương trình (1) có hai nghiệm \({x_1};{x_2}\) thỏa mãn điều kiện \(\dfrac{{{x_1} - 1}}{{2{x_2}}} - \dfrac{{{x_2} - 1}}{{2{x_1}}} = - 3\).
Để phương trình có hai nghiệm phân biệt \( \Leftrightarrow \Delta ' > 0 \Leftrightarrow 3 - m > 0 \Leftrightarrow m < 3\)
Áp dụng định lý Vi-et, ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = - 4\\{x_1}{x_2} = m + 1\,\,\left( * \right)\end{array} \right.\)
\( \Rightarrow {x_2} = - 4 - {x_1}\) . Thay vào \(\dfrac{{{x_1} - 1}}{{2{x_2}}} - \dfrac{{{x_2} - 1}}{{2{x_1}}} = - 3\), ta có:
\(\begin{array}{l}\dfrac{{{x_1} - 1}}{{2\left( { - 4 - {x_1}} \right)}} - \dfrac{{ - 4 - {x_1} - 1}}{{2{x_1}}} = - 3,\,\,\left( {{x_1} \ne 0,\,\,{x_1} \ne 4} \right)\\ \Leftrightarrow \dfrac{{{x_1} - 1}}{{2( - 4 - {x_1})}} - \dfrac{{ - 5 - {x_1}}}{{2{x_1}}} = - 3\\ \Leftrightarrow \dfrac{{{x_1}\left( {{x_1} - 1} \right) - \left( { - 4 - {x_1}} \right)\left( { - 5 - {x_1}} \right)}}{{2{x_1}( - 4 - {x_1})}} = - 3\\ \Leftrightarrow {x_1}\left( {{x_1} - 1} \right) - \left( {4 + {x_1}} \right)\left( {5 + {x_1}} \right) = - 3.2{x_1}( - 4 - {x_1})\\ \Leftrightarrow x_1^2 - {x_1} - 20 - 4{x_1} - 5{x_1} - x_1^2 - 24{x_1} - 6x_1^2 = 0\\ \Leftrightarrow - 6x_1^2 - 34{x_1} - 20 = 0\\ \Leftrightarrow 3x_1^2 + 17{x_1} + 10 = 0\\ \Leftrightarrow 3x_1^2 + 15{x_1} + 2{x_1} + 10 = 0\\ \Leftrightarrow 3{x_1}\left( {{x_1} + 5} \right) + 2\left( {{x_1} + 5} \right) = 0\\ \Leftrightarrow \left( {{x_1} + 5} \right)\left( {3{x_1} + 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}{x_1} = - 5\\{x_1} = - \dfrac{2}{3}\end{array} \right.\end{array}\)
Với \({x_1} = - 5 \) \(\Rightarrow {x_2} = - 4 - {x_1} = - 4 + 5 = 1\)
Thay vào (*) ta có \( - 5 = m + 1 \Leftrightarrow m = - 6\,\,\left( {tm} \right)\)
Với \({x_1} = - \dfrac{2}{3} \Rightarrow {x_2} = - 4 - {x_1} = - \dfrac{{10}}{3}\)
Thay vào (*) ta có \(\dfrac{{20}}{9} = m + 1 \Leftrightarrow m = \dfrac{{11}}{9}\,\,\left( {tm} \right)\)
Vậy \(m = - 6\) hoặc \(m = \dfrac{{11}}{9}\).
Câu 4.
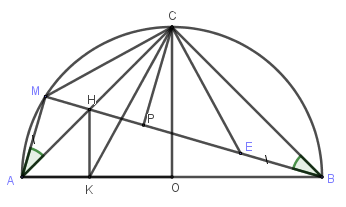
a) Chứng minh tứ giác CHKB là tứ giác nội tiếp.
Xét tứ giác BCHK có:
\(\widehat {HCB} = {90^0}\) (góc nội tiếp chắn nửa đường tròn)
\(\widehat {HKB} = {90^0}\) (giả thiết)
\( \Rightarrow \widehat {HCB} + \widehat {HKB} = {90^0} + {90^0} = {180^0}\).
Vậy tứ giác \(CHKB\) là tứ giác nội tiếp (đpcm).
b) Chứng minh CA là phân giác của góc MCK.
- Tứ giác BCHK nội tiếp nên \(\widehat {ACK} = \widehat {MBA}\) (góc nội tiếp cùng chắn cung \(HK\)).
- \(\widehat {MCA} = \widehat {MBA}\) (góc nội tiếp cùng chắn cung MA của đường tròn tâm (O)).
Do đó \(\widehat {ACK} = \widehat {MBA} = \widehat {MCA}\) hay \(CA\) là tia phân giác của \(\widehat {MCK}\) (đpcm).
c) Chứng minh ME = 2CP.
Xét \(\Delta CMA\) và \(\Delta CEB\) có:
\(MA = EB\left( {gt} \right)\)
\(\widehat {MAC} = \widehat {EBC}\) (cùng chắn cung MC của đường tròn (O))
\(CA = CB\) (\(\Delta CAB\) vuông cân)
Do đó \(\Delta CMA = \Delta CEB\left( {c.g.c} \right)\)
\( \Rightarrow CM = CE\) (cạnh tương ứng) \( \Rightarrow \Delta CME\) cân tại \(C\).
Lại có \(\widehat {CMB} = \widehat {CAB} = {45^0}\) (cùng chắn cung \(CB\)) nên \(\widehat {CEM} = {45^0} \Rightarrow \widehat {MCE} = {90^0}\).
Vậy \(\Delta CME\) vuông cân tại \(C\).
Mà \(CP \bot ME\,\,\left( {gt} \right)\) nên \(CP\) là đường cao và cũng là đường trung tuyến của \(\Delta CME\).
Do đó \(PM = PE = CP \Rightarrow ME = 2CP\) (đpcm).
Loigiaihay.com













Danh sách bình luận