Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học Tổng hợp 50 đề thi vào 10 môn Toán

Đề số 1 - Đề thi vào lớp 10 môn Toán


Đề thi vào lớp 10 môn Toán - Đề số 1 có đáp án và lời giải chi tiết

Đề bài

Bài 1 (1,5 điểm)

1) Rút gọn biểu thức \(A = {\left( {\sqrt 5  - \sqrt 2 } \right)^2} + \sqrt {40} \)

2) Rút gọn biểu thức \(B = \left( {\dfrac{{x - \sqrt x }}{{\sqrt x  - 1}} - \dfrac{{\sqrt x  + 1}}{{x + \sqrt x }}} \right):\dfrac{{\sqrt x  + 1}}{{\sqrt x }}\) với \(x > 0,\,\,x \ne 1\)

Tính giá trị của B khi \(x = 12 + 8\sqrt 2 \)

Bài 2 (1,5 điểm)

Cho Parabol \(\left( P \right):\;\;y =  - {x^2}\) và đường thẳng \(\left( d \right):\;\;y = 2\sqrt 3 x + m + 1\) (m là tham số).

1) Vẽ đồ thị hàm số (P).

2) Tìm tất cả các giá trị của tham số m để (d) cắt (P) tại hai điểm phân biệt.

Bài 3 (2,0 điểm)

1) Giải hệ phương trình: \(\left\{ \begin{array}{l}9x + y = 11\\5x + 2y = 9\end{array} \right.\)

2) Cho phương trình: \({x^2} - 2\left( {m + 2} \right)x + {m^2} + 3m - 2 = 0\,\,\left( 1 \right)\), (m là tham số)

a. Giải phương trình (1) khi m = 3.

b. Tìm các giá trị của tham số m để phương trình (1)  có hai nghiệm phân biệt \({x_1},{x_2}\) sao cho biểu thức \(A = 2018 + 3{x_1}{x_2} - x_1^2 - x_2^2\) đạt giá trị nhỏ nhất.

Bài 4  (1,5 điểm)

Một người dự định đi xe máy từ tỉnh A đến tỉnh B cách nhau 90 km trong một thời gian đã định. Sau khi đi được 1 giờ, người đó nghỉ 9 phút. Do đó, để đến tỉnh B đúng hẹn, người ấy phải tăng vận tốc thêm 4 km/h. Tính vận tốc lúc đấy của người đó.

Bài 5  (3,5 điểm)

Cho tam giác ABC có ba góc nhọn nội tiếp trong đường tròn (O) có bán kính \(R = 3cm\). Các tiếp tuyến với (O) tại B và C cắt nhau tại D.

1) Chứng minh tứ giác OBDC nội tiếp đường tròn.

2) Gọi M là giao điểm của BC và OD. Biết \(OD = 5cm\). Tính diện tích của tam giác BCD.

3) Kẻ đường thẳng d đi qua D và song song với đường tiếp tuyến với (O) tại A, d cắt các đường thẳng AB, AC lần lượt tại P, Q. Chứng minh \(AB.AP = AQ.AC\)

4) Chứng minh góc PAD bằng góc MAC.

Lời giải chi tiết

Bài 1.

\(\begin{array}{l}1)\,\,A = {\left( {\sqrt 5  - \sqrt 2 } \right)^2} + \sqrt {40} \\\,\,\,\,\,\;\;\; = {\left( {\sqrt 5 } \right)^2} - 2\sqrt 5 .\sqrt 2  + {\left( {\sqrt 2 } \right)^2} + \sqrt {{2^2}.10} \\\,\,\,\,\,\;\;\; = 5 - 2\sqrt {10}  + 2 + 2\sqrt {10} \\\,\,\,\,\,\;\;\; = 7.\\2)\,\,B = \left( {\dfrac{{x - \sqrt x }}{{\sqrt x  - 1}} - \dfrac{{\sqrt x  + 1}}{{x + \sqrt x }}} \right):\dfrac{{\sqrt x  + 1}}{{\sqrt x }}\,\,\,\left( {x > 0,\,\,x \ne 1} \right)\\\;\;\;\;\;\;\; = \left( {\dfrac{{\sqrt x \left( {\sqrt x  - 1} \right)}}{{\sqrt x  - 1}} - \dfrac{{\sqrt x  + 1}}{{\sqrt x \left( {\sqrt x  + 1} \right)}}} \right):\dfrac{{\sqrt x  + 1}}{{\sqrt x }}\\\;\;\;\;\;\;\; = \left( {\sqrt x  - \dfrac{1}{{\sqrt x }}} \right).\dfrac{{\sqrt x }}{{\sqrt x  + 1}}\\\;\;\;\;\;\;\; = \dfrac{{x - 1}}{{\sqrt x }}.\dfrac{{\sqrt x }}{{\sqrt x  + 1}}\\\;\;\;\;\;\;\; = \dfrac{{\left( {\sqrt x  + 1} \right)\left( {\sqrt x  - 1} \right)}}{{\sqrt x  + 1}}\\\,\,\,\,\,\,\,\,\,\, = \sqrt x  - 1\,\,\end{array}\)

Ta có

\(\begin{array}{l}x = 12 + 8\sqrt 2  = {\left( {2\sqrt 2 } \right)^2} + 2.2\sqrt 2 .2 + {2^2} = {\left( {2\sqrt 2  + 2} \right)^2}\\ \Rightarrow \sqrt x  = \sqrt {{{\left( {2\sqrt 2  + 2} \right)}^2}}  = \left| {2\sqrt 2  + 2} \right| = 2\sqrt 2  + 2\\\left( {Do\,\,2\sqrt 2  + 2 > 0} \right)\end{array}\)

Thay \(\sqrt x  = 2\sqrt 2  + 2\) vào B ta có \(B = \sqrt x  - 1 = 2\sqrt 2  + 2 - 1 = 2\sqrt 2  + 1\).

Vậy khi \(x = 12 + 8\sqrt 2 \) thì \(B = 2\sqrt 2  + 1\)

Bài 2:

1) Vẽ đồ thị hàm số \(\left( P \right):\;\;y =  - {x^2}\):

Ta có bảng giá trị:

\(x\)

-2

-1

0

1

2

\(\;y =  - {x^2}\)

-4

-1

0

-1

-4

Đồ thị hàm số:

                                  

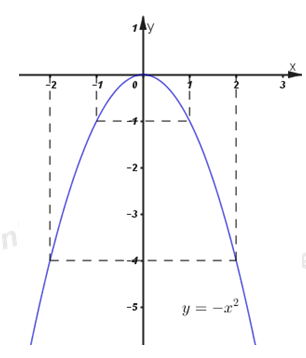
2) Phương trình hoành độ giao điểm của hai đồ thị hàm số là: \( - {x^2} = 2\sqrt 3 x + m + 1\)

\( \Leftrightarrow {x^2} + 2\sqrt 3 x + m + 1 = 0\;\;\;\left( * \right)\)

Để (d) cắt (P) tại hai điểm phân biệt thì phương trình (*) phải có hai nghiệm phân biệt \( \Leftrightarrow \Delta ' > 0\)

\(\begin{array}{l} \Leftrightarrow {\left( {\sqrt 3 } \right)^2} - m - 1 > 0\\ \Leftrightarrow 2 - m > 0\\ \Leftrightarrow m < 2.\end{array}\)

Vậy với \(m < 2\) thì đường thẳng \(\left( d \right)\) cắt đồ thị hàm số \(\left( P \right)\) tại hai điểm phân biệt.

Bài 3

Ta có:

\(\left\{ \begin{array}{l}9x + y = 11\\5x + 2y = 9\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 11 - 9x\\5x + 2y = 9\end{array} \right. \)

\(\Leftrightarrow \left\{ \begin{array}{l}y = 11 - 9x\\5x + 2\left( {11 - 9x} \right) = 9\end{array} \right. \)

\(\Leftrightarrow \left\{ \begin{array}{l}y = 11 - 9x\\5x + 22 - 18x - 9 = 0\end{array} \right. \)

\(\Leftrightarrow \left\{ \begin{array}{l}y = 11 - 9x\\x = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 2\\x = 1\end{array} \right.\)

Vậy hệ phương trình có 1 nghiệm duy nhất \(\left( {x;y} \right) = \left( {1;2} \right)\)

1)  Cho phương trình: \({x^2} - 2\left( {m + 2} \right)x + {m^2} + 3m - 2 = 0\,\,\left( 1 \right)\), ( m là tham số)

a)  Giải phương trình (1) khi m = 3.

Với m = 3 ta có (1) trở thành:

\({x^2} - 10x + 16 = 0\,\,\left( 2 \right)\)

Ta có: \(\Delta ' = {\left( { - 5} \right)^2} - 16 = 9 > 0\)

Khi đó phương trình (2) có 2 nghiệm phân biệt là: 

\(\left[ \begin{array}{l}{x_1} = 5 - 3 = 2\\{x_2} = 5 + 3 = 8\end{array} \right.\)

Vậy với m = 3 thì phương trình (1) có tập nghiệm là: \(S = \left\{ {2;8} \right\}\)

b)  Tìm các giá trị của tham số m để phương trình (1)  có hai nghiệm phân biệt \({x_1},{x_2}\) sao cho biểu thức \(A = 2018 + 3{x_1}{x_2} - x_1^2 - x_2^2\) đạt giá trị nhỏ nhất.

+) Phương trình (1) có hai nghiệm phân biệt \({x_1},{x_2}\) khi và chỉ khi \(\Delta ' > 0\)

\(\begin{array}{l} \Leftrightarrow {\left[ { - \left( {m + 2} \right)} \right]^2} - \left( {{m^2} + 3m - 2} \right) > 0\\ \Leftrightarrow {m^2} + 4m + 4 - {m^2} - 3m + 2 > 0\\ \Leftrightarrow m >  - 6\end{array}\)

+) Áp dụng hệ thức Viet cho phương trình (1) ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2\left( {m + 2} \right)\\{x_1}{x_2} = {m^2} + 3m - 2\end{array} \right.\)

Ta có:

\(\begin{array}{l}A = 2018 + 3{x_1}{x_2} - x_1^2 - x_2^2\\\,\,\,\,\, = 2018 + 3{x_1}{x_2} - \left[ {{{\left( {{x_1} + {x_2}} \right)}^2} - 2{x_1}{x_2}} \right]\\\,\,\,\,\, = 2018 + 5{x_1}{x_2} - {\left( {{x_1} + {x_2}} \right)^2}\end{array}\)

Thay Viet vào A ta được:

\(\begin{array}{l}A = 2018 + 5{x_1}{x_2} - {\left( {{x_1} + {x_2}} \right)^2}\\ = 2018 + 5\left( {{m^2} + 3m - 2} \right) - 4{\left( {m + 2} \right)^2}\\ = 2018 + 5{m^2} + 15m - 10 - 4{m^2} - 16m - 16\\ = {m^2} - m + 1992\\ = {\left( {m - \dfrac{1}{2}} \right)^2} + \dfrac{{7967}}{4}\,\,\,\,\,\end{array}\)

Ta có: \(A \ge \dfrac{{7967}}{4}\). Dấu “=” xảy ra khi và chỉ khi \(m = \dfrac{1}{2}\left( {tm} \right)\)

Vậy \(m = \dfrac{1}{2}\) thỏa mãn yêu cầu bài toán.

Bài 4:

Gọi vận tốc ban đầu của người đó là \(x\;\;\left( {km/h} \right),\;\;\left( {x > 0} \right).\)

Thời gian dự định người đó đi hết quãn đường là: \(\dfrac{{90}}{x}\;\;\left( h \right).\)

Quãng đường người đó đi được sau 1 giờ là: \(x\;\;\left( {km} \right).\)

Quãng đường còn lại người đó phải tăng tốc là: \(90 - x\;\;\left( {km} \right).\)

Vận tốc của người đó sau khi tăng tốc là: \(x + 4\;\;\left( {km/h} \right),\) thời gian người đó đi hết quãng đường còn lại là: \(\dfrac{{90 - x}}{{x + 4}}\;\;\left( h \right).\)

Theo đề bài ta có phương trình:

\(\begin{array}{l}\dfrac{{90}}{x} = 1 + \dfrac{9}{{60}} + \dfrac{{90 - x}}{{x + 4}}\\ \Leftrightarrow \dfrac{{90}}{x} = \dfrac{{23}}{{20}} + \dfrac{{90 - x}}{{x + 4}}\\ \Leftrightarrow 90.20\left( {x + 4} \right) = 23x\left( {x + 4} \right) + 20.\left( {90 - x} \right).x\\ \Leftrightarrow 1800x + 7200 = 23{x^2} + 92x + 1800x - 20{x^2}\\ \Leftrightarrow 3{x^2} + 92x - 7200 = 0\\ \Leftrightarrow \left( {x - 36} \right)\left( {3x + 200} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 36 = 0\\3x + 200 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 36\;\;\left( {tm} \right)\\x =  - \dfrac{{200}}{3}\;\;\left( {ktm} \right)\end{array} \right..\end{array}\)

Vậy vận tốc lúc đầu của người đó là \(36\;km/h.\)

Bài 5.

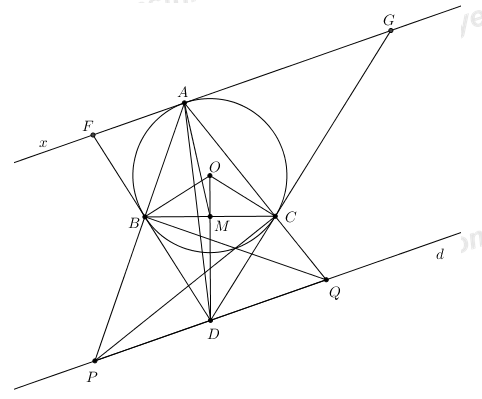
1) Chứng minh tứ giác OBDC nội tiếp đường tròn.

Do DB, DC là các tiếp tuyến của đường tròn (O) \( \Rightarrow \widehat {OBD} = \widehat {OCD} = {90^0}\)

Xét tứ giác OBDC có  \(\widehat {OBD} + \widehat {OCD} = {90^0} + {90^0} = {180^0}\) \( \Rightarrow \) tứ giác OBDC là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 1800)

2) Gọi M là giao điểm của BC và OD. Biết \(OD = 5cm\). Tính diện tích của tam giác BCD.

Áp dụng định lí Pitago trong tam giác vuông OBD có \(BD = \sqrt {O{D^2} - O{B^2}}  = \sqrt {{5^2} - {3^2}}  = 4\,\,\left( {cm} \right)\)

Ta có \(OB = OC = R;\,\,DB = DC\) (tính chất hai tiếp tuyến cắt nhau)

\( \Rightarrow O;\,\,D\) thuộc trung trực của BC \( \Rightarrow OD\) là trung trực của BC \( \Rightarrow OD \bot BC\).

Áp dụng hệ thức lượng trong tam giác vuông OBD có:

\(DM.DO = D{B^2} \) \(\Rightarrow DM = \dfrac{{D{B^2}}}{{DO}} = \dfrac{{{4^2}}}{5} = \dfrac{{16}}{5}\,\,\left( {cm} \right)\)

\(BM.OD = OB.BD\) \( \Rightarrow BM = \dfrac{{OB.BD}}{{OD}} = \dfrac{{3.4}}{5} = \dfrac{{12}}{5}\,\,\left( {cm} \right)\)

Vậy \({S_{\Delta DBC}} = \dfrac{1}{2}DM.BC = DM.BM \)\(\,= \dfrac{{16}}{5}.\dfrac{{12}}{5} = \dfrac{{192}}{{25}} = 7,68\,\,\left( {c{m^2}} \right)\)

3) Kẻ đường thẳng d đi qua D và song song với đường tiếp tuyến với (O) tại A, d cắt các đường thẳng AB, AC lần lượt tại P, Q. Chứng minh \(AB.AP = AQ.AC\)

Ta có \(\widehat {APQ} = \widehat {xAB}\) ( 2 góc so le trong do đường thẳng Ax // PQ)

Mà \(\widehat {xAB} = \widehat {ACB}\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung AB của (O)).

\( \Rightarrow \widehat {APQ} = \widehat {ACB}\)

Xét tam giác ABC và tam giác AQP có:

\(\widehat {PAQ}\) chung;

\(\widehat {APQ} = \widehat {ACB}\,\,\left( {\,cmt} \right)\)

\( \Rightarrow \Delta ABC \sim \Delta AQP\,\,\left( {g.g} \right) \)

\(\Rightarrow \dfrac{{AB}}{{AQ}} = \dfrac{{AC}}{{AP}} \)

\(\Rightarrow AB.AP = AC.AQ\)

4) Chứng minh góc PAD bằng góc MAC.

Kéo dài BD cắt D tại F.

Ta có \(\widehat {DBP} = \widehat {ABF}\) (đối đỉnh)

Mà \(\widehat {ABF} = \widehat {ACB}\) (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung AB)

\(\widehat {ACB} = \widehat {APD}\) (do )

\( \Rightarrow \widehat {DBP} = \widehat {APD} = \widehat {BPD} \Rightarrow \Delta DBP\) cân tại D \( \Rightarrow DB = DP\)

Tương tự kéo dài DC cắt d tại G, ta chứng minh được \(\widehat {DCQ} = \widehat {ACG} = \widehat {ABC} = \widehat {DQC} \Rightarrow \Delta DCQ\) cân tại D \( \Rightarrow DC = DQ\)

Lại có \(DB = DC\) (tính chất hai tiếp tuyến cắt nhau) \( \Rightarrow DP = DQ \Rightarrow D\) là trung điểm của PQ.

Ta có: \(\Delta ABC \sim \Delta AQP\,\,\left( {cmt} \right)\)

\(\Rightarrow \dfrac{{AB}}{{AQ}} = \dfrac{{AC}}{{AP}} = \dfrac{{BC}}{{PQ}} = \dfrac{{2MC}}{{2PD}} \)

\(\Rightarrow \dfrac{{AC}}{{AP}} = \dfrac{{MC}}{{PD}}\)

Xét tam giác \(AMC\) và tam giác \(ADP\) có

\(\widehat {ACM} = \widehat {APD}\,\,\left( {\widehat {ACB} = \widehat {APQ}\,\,\left( {cmt} \right)} \right)\)

\(\dfrac{{AC}}{{AP}} = \dfrac{{MC}}{{PD}}\,\,\left( {cmt} \right)\)

\( \Rightarrow \Delta AMC \sim \Delta ADP\,\,\left( {c.g.c} \right)\)

\(\Rightarrow \widehat {PAD} = \widehat {MAC}\,\,\left( {dpcm} \right)\)

Loigiaihay.com


Bình chọn:
4.5 trên 37 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store