Đề kiểm tra giữa kì 2 Toán 10 - đề số 7 có lời giải chi tiết

Đề bài

Câu 1 (4,0 điểm): Giải các bất phương trình sau:

a) \(x\left( {2x - 3} \right) \le  - 3x\left( {x - 1} \right) - 1\)

b) \(\dfrac{1}{{2x - 1}} \ge \dfrac{4}{{x - 3}}\)

c) \(\sqrt {{x^2} - 2x - 3}  > 2x - 3\) 

d) \(\left| {{x^2} + 3x + 2} \right| <  - x + 2\)

Câu 2 (1,5 điểm): Cho hàm số \(y = f\left( x \right) = 2{x^2} - mx + 3m - 2\) và \(y = g\left( x \right) = m{x^2} - 2x + 4m - 5\).

Tìm tất cả các giá trị của tham số \(m\) để \(f\left( x \right) \ge g\left( x \right)\), \(\forall x \in \mathbb{R}\).

Câu 3 (1,5 điểm): Cho tam giác \(ABC\) với \(AB = 3,\,\,AC = 7,\,\,BC = 8\). Hãy tính diện tích tam giác và các bán kính đường tròn ngoại tiếp, nội tiếp của tam giác \(ABC\).

Câu 4 (2,5 điểm): Trong mặt phẳng tọa độ \(Oxy\), cho hai điểm \(A\left( { - 1;\,\,2} \right)\),\(B\left( {3;\,\,1} \right)\) và đường thẳng \(\left( d \right):\left\{ \begin{array}{l}x = 1 + t\\y = 2 + t\end{array} \right.\) (\(t\) là tham số)

a) Lập phương trình tổng quát của đường thẳng \(\left( {d'} \right)\) đi qua \(A\) và vuông góc với \(\left( d \right)\).

b) Tìm tọa độ điểm \(A'\) đối xứng với \(A\) qua \(\left( d \right)\).

c) Tìm tọa độ điểm \(M\) trên \(\left( d \right)\) sao cho \(M\) cách \(B\) một khoảng bằng \(\sqrt 5 \).

Câu 5 (0,5 điểm): Giải phương trình \(4x\sqrt {x + 3}  + 2\sqrt {2x - 1}  = 4{x^2} + 3x + 3\).

Lời giải chi tiết

Câu 1 (VD) - Bất phương trình

Phương pháp:

a) Đưa về phương trình bậc hai và lập bảng xét dấu.

b) Tìm ĐKXĐ. Quy đồng sau đó lập bảng xét dấu.

c) Áp dụng \(\sqrt {f\left( x \right)}  > g\left( x \right)\)\( \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}f\left( x \right) \ge 0\\g\left( x \right) < 0\end{array} \right.\\\left\{ \begin{array}{l}g\left( x \right) \ge 0\\f\left( x \right) > {g^2}\left( x \right)\end{array} \right.\end{array} \right.\)

d) Áp dụng \(\left| {f\left( x \right)} \right| \le a\)\( \Leftrightarrow  - a \le f\left( x \right) \le a\)

Cách giải:

Giải các bất phương trình sau:

a) \(x\left( {2x - 3} \right) \le  - 3x\left( {x - 1} \right) - 1\)

\(\begin{array}{l}\,\,\,\,\,\,x\left( {2x - 3} \right) \le  - 3x\left( {x - 1} \right) - 1\\ \Leftrightarrow 2{x^2} - 3x \le  - 3{x^2} + 3x - 1\\ \Leftrightarrow 2{x^2} - 3x + 3{x^2} - 3x + 1 \le 0\\ \Leftrightarrow 5{x^2} - 6x + 1 \le 0\end{array}\)

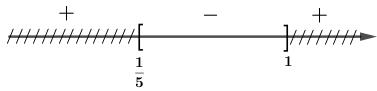
Vậy bất phương trình có tập nghiệm là \(S = \left[ {\dfrac{1}{5};\,\,1} \right]\).

b) \(\dfrac{1}{{2x - 1}} \ge \dfrac{4}{{x - 3}}\)

\(\begin{array}{l}\,\,\,\,\,\,\,\dfrac{1}{{2x - 1}} \ge \dfrac{4}{{x - 3}}\\ \Leftrightarrow \dfrac{1}{{2x - 1}} \ge \dfrac{4}{{x - 3}}\\ \Leftrightarrow \dfrac{1}{{2x - 1}} - \dfrac{4}{{x - 3}} \ge 0\end{array}\)                                                  ĐKXĐ: \(\left\{ \begin{array}{l}2x - 1 \ne 0\\x - 3 \ne 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x \ne \dfrac{1}{2}\\x \ne 3\end{array} \right.\)

\(\begin{array}{l} \Leftrightarrow \dfrac{{\left( {x - 3} \right) - 4\left( {2x - 1} \right)}}{{\left( {x - 3} \right)\left( {2x - 1} \right)}} \ge 0\\ \Leftrightarrow \dfrac{{x - 3 - 8x + 4}}{{2{x^2} - x - 6x + 3}} \ge 0\\\,\, \Leftrightarrow \dfrac{{ - 7x + 1}}{{2{x^2} - 7x + 3}} \ge 0\end{array}\)

Ta có bảng xét dấu:

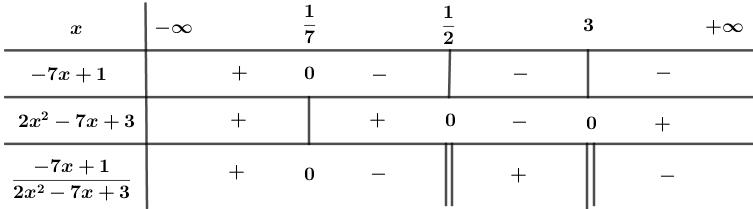
Vậy bất phương trình có tập nghiệm là \(S = \left( { - \infty ;\,\,\dfrac{1}{7}} \right] \cup \left( {3;\,\, + \infty } \right)\).

c) \(\sqrt {{x^2} - 2x - 3}  > 2x - 3\)

\(\begin{array}{l}\,\,\sqrt {{x^2} - 2x - 3}  > 2x - 3\\ \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}{x^2} - 2x - 3 \ge 0\\2x - 3 < 0\end{array} \right.\\\left\{ \begin{array}{l}2x - 3 \ge 0\\{x^2} - 2x - 3 > {\left( {2x - 3} \right)^2}\end{array} \right.\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}\left[ \begin{array}{l}x \le  - 1\\x \ge 3\end{array} \right.\\x < \dfrac{3}{2}\end{array} \right.\\\left\{ \begin{array}{l}x \ge \dfrac{3}{2}\\ - 3{x^2} + 10x - 12 > 0\,\,\,\,\left( {VN} \right)\end{array} \right.\end{array} \right.\\ \Leftrightarrow x \le  - 1\end{array}\)

Vậy tập nghiệm của bất phương trình là \(S = \left( { - \infty ;\,\, - 1} \right]\).

d) \(\left| {{x^2} + 3x + 2} \right| <  - x + 2\)

\(\begin{array}{l}\,\,\,\,\,\,\,\left| {{x^2} + 3x + 2} \right| <  - x + 2\\ \Leftrightarrow x - 2 < {x^2} + 3x + 2 <  - x + 2\\ \Leftrightarrow \left\{ \begin{array}{l}x - 2 < {x^2} + 3x + 2\\{x^2} + 3x + 2 <  - x + 2\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{x^2} + 2x + 4 > 0\,\,\,\forall x\\{x^2} + 4x < 0\end{array} \right.\\ \Leftrightarrow  - 4 < x < 0\end{array}\)

Vậy bất phương trình có tập nghiệm là \(S = \left( { - 4;\,\,0} \right)\).

Câu 2 (VD) - Bất phương trình

Phương pháp:

Đưa biểu thức về dạng \(f\left( x \right) - g\left( x \right) \ge 0\).

\(P\left( x \right) \ge 0\,\,\forall x \in \mathbb{R} \Leftrightarrow \left\{ \begin{array}{l}a > 0\\\Delta  \le 0\end{array} \right.\)

Cách giải:

Cho hàm số \(y = f\left( x \right) = 2{x^2} - mx + 3m - 2\) và \(y = g\left( x \right) = m{x^2} - 2x + 4m - 5\).

Tìm tất cả các giá trị của tham số \(m\) để \(f\left( x \right) \ge g\left( x \right)\), \(\forall x \in \mathbb{R}\).

Theo đề bài, ta có:

\(\begin{array}{l}f\left( x \right) \ge g\left( x \right)\,\forall x \in \mathbb{R}\\ \Leftrightarrow 2{x^2} - mx + 3m - 2\\ \ge m{x^2} - 2x + 4m - 5\,\,\forall x \in \mathbb{R}\\ \Leftrightarrow 2{x^2} - mx + 3m - 2 - m{x^2} \\+ 2x - 4m + 5 \ge 0\,\forall x \in \mathbb{R}\\ \Leftrightarrow \left( {2 - m} \right){x^2} + \left( {2 - m} \right)x - m\\ + 3 \ge 0\,\,\forall x \in \mathbb{R}\end{array}\)

TH1 : \(2 - m = 0 \Leftrightarrow m = 2\)

Bất phương trình trở thành \( - 2 + 3 \ge 0 \Leftrightarrow 1 \ge 0\) (luôn đúng)

TH2 : \(2 - m \ne 0 \Leftrightarrow m \ne 2\)

 Để\(\left( {2 - m} \right){x^2} + \left( {2 - m} \right)x - m + 3 \ge 0\,\,\forall x \in \mathbb{R}\)\( \Leftrightarrow \left\{ \begin{array}{l}2 - m > 0\\\Delta  \le 0\end{array} \right.\)

\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}m < 2\\{\left( {2 - m} \right)^2} - 4.\left( {2 - m} \right).\left( { - m + 3} \right) \le 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}m < 2\\ - 3{m^2} + 16m - 20 \le 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}m < 2\\\left[ \begin{array}{l}m \ge \dfrac{{10}}{3}\\m \le 2\end{array} \right.\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}m < 2\\m \ge \dfrac{{10}}{3}\end{array} \right.\\\left\{ \begin{array}{l}m < 2\\m \le 2\end{array} \right.\end{array} \right. \Leftrightarrow m < 2\end{array}\)

Kết hợp hai trường hợp trên, ta được \(m \le 2\)

Vậy \(m < 2\) thì \(f\left( x \right) \ge g\left( x \right)\), \(\forall x \in \mathbb{R}\).

Câu 3 (VD) - Các hệ thức lượng trong tam giác và giải tam giác

Phương pháp:

Tính nửa chu vi của tam giác \(ABC\).

Áp dụng các công thức:

+ Công thức Hê-rông \({S_{\Delta ABC}} = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} \)

+ \({S_{\Delta ABC}} = \dfrac{{abc}}{{4R}}\), \({S_{\Delta ABC}} = p.r\)

Cách giải:

Cho tam giác \(ABC\) với \(AB = 3,\,\,AC = 7,\,\,BC = 8\). Hãy tính diện tích tam giác và các bán kính đường tròn ngoại tiếp, nội tiếp của tam giác \(ABC\).

Đặt \(a = BC = 8,\,\,b = AC = 7,\,\,c = AB = 3\).

\({p_{\Delta ABC}} = \dfrac{{a + b + c}}{2} = \dfrac{{8 + 7 + 3}}{2} = 9\)

Áp dụng công thức Hê-rông ta có:  \({S_{\Delta ABC}} = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} \)\( = \sqrt {9.\left( {9 - 8} \right).\left( {9 - 7} \right).\left( {9 - 3} \right)} \)

Ta lại có:

\({S_{\Delta ABC}} = \dfrac{{abc}}{{4R}}\)\( \Rightarrow R = \dfrac{{abc}}{{4{S_{\Delta ABC}}}}\)\( = \dfrac{{3.7.8}}{{4.6.\sqrt 3 }} = \dfrac{7}{{\sqrt 3 }}\)

\({S_{\Delta ABC}} = p.r\)\( \Rightarrow r = \dfrac{{{S_{\Delta ABC}}}}{p}\)\( = \dfrac{{6.\sqrt 3 }}{9} = \dfrac{{2\sqrt 3 }}{3}\)

Câu 4 (VD) - Phương trình đường thẳng

Phương pháp:

a) \(\left( d \right) \bot \left( {d'} \right) \Leftrightarrow {\vec n_{d'}}.{\vec n_d} = 0\)

\( \Rightarrow \left( d \right)\) đi qua \(A\left( { - 1;\,\,2} \right)\) nhận \({\vec n_d}\) là VTPT

b) Giả sử \(\left( d \right) \cap \left( {d'} \right) = H\)\( \Rightarrow \) \(H\) là trung điểm của \(AA'\). Tọa độ điểm \(H\) là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}{x_H} = 1 + t\\{y_H} = 2 + t\\{x_H} + {y_H} - 1 = 0\end{array} \right.\).

c) \(M \in \left( d \right):\left\{ \begin{array}{l}x = 1 + t\\y = 2 + t\end{array} \right.\) \( \Rightarrow M\left( {1 + t;\,\,2 + t} \right)\)sau đó áp dụng công thức tính độ dài véc tơ để tìm tọa độ điểm M .

Cách giải:

Trong mặt phẳng tọa độ \(Oxy\), cho hai điểm \(A\left( { - 1;\,\,2} \right)\), \(B\left( {3;\,\,1} \right)\) và đường thẳng \(\left( d \right):\left\{ \begin{array}{l}x = 1 + t\\y = 2 + t\end{array} \right.\) (\(t\) là tham số)

a) Lập phương trình tổng quát của đường thẳng \(\left( {d'} \right)\) đi qua \(A\) và vuông góc với \(\left( d \right)\).

\(\left( d \right):\left\{ \begin{array}{l}x = 1 + t\\y = 2 + t\end{array} \right.\)\( \Rightarrow {\vec u_d} = \left( {1;\,\,1} \right)\)

Vì \(\left( d \right) \bot \left( {d'} \right)\)\( \Rightarrow {\vec n_{d'}} = {\vec u_d} = \left( {1;\,\,1} \right)\).

Phương trình tổng quát của đường thẳng \(\left( {d'} \right)\) đi qua \(A\left( { - 1;\,\,2} \right)\) có VTPT \({\vec n_{d'}} = \left( {1;\,\,1} \right)\) là :

\(\begin{array}{l}1.\left( {x + 1} \right) + 1.\left( {y - 2} \right) = 0\\ \Leftrightarrow x + y - 1 = 0\end{array}\)

Vậy phương trình tổng quát của đường thẳng \(\left( {d'} \right):\,\,x + y - 1 = 0\).

b) Tìm tọa độ điểm \(A'\) đối xứng với \(A\) qua \(\left( d \right)\).

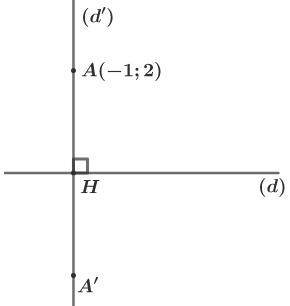
Theo đề bài, \(A'\) đối xứng với \(A\) qua \(\left( d \right)\) nên \(\left( d \right)\) là đường trung trực của \(AA'\).

\( \Rightarrow \left( d \right) \bot AA'\) mà \(A \in \left( {d'} \right)\) và \(\left( d \right) \bot \left( {d'} \right)\)

\( \Rightarrow A' \in \left( {d'} \right)\)

Giả sử \(\left( d \right) \cap \left( {d'} \right) = H\)\( \Rightarrow \) \(H\) là trung điểm của \(AA'\).

Tọa độ điểm \(H\left( {{x_H};\,\,{y_H}} \right)\) là nghiệm của hệ phương trình:

\(\begin{array}{l}\left\{ \begin{array}{l}{x_H} = 1 + t\\{y_H} = 2 + t\\{x_H} + {y_H} - 1 = 0\end{array} \right.\\ \Rightarrow \left( {1 + t} \right) + \left( {2 + t} \right) - 1 = 0\\ \Leftrightarrow 2t + 2 = 0\\ \Leftrightarrow t =  - 1\end{array}\)

\( \Rightarrow \left\{ \begin{array}{l}{x_H} = 1 + \left( { - 1} \right)\\{y_H} = 2 + \left( { - 1} \right)\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}{x_H} = 0\\{y_H} = 1\end{array} \right.\)\( \Rightarrow H\left( {0;\,\,1} \right)\)

Vì \(H\) là trung điểm của \(AA'\) nên

\(\left\{ \begin{array}{l}{x_A} = 2{x_H} - {x_{A'}}\\{y_A} = 2{y_H} - {y_{A'}}\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}{x_A} = 1\\{y_A} = 2\end{array} \right.\) \( \Rightarrow A'\left( {1;\,\,0} \right)\)

c) Tìm tọa độ điểm \(M\) trên \(\left( d \right)\) sao cho \(M\) cách \(B\) một khoảng bằng \(\sqrt 5 \).

\(M \in \left( d \right):\left\{ \begin{array}{l}x = 1 + t\\y = 2 + t\end{array} \right.\)\( \Rightarrow M\left( {1 + t;\,\,2 + t} \right)\)

Có \(B\left( {3;\,\,1} \right)\)\( \Rightarrow \overrightarrow {MB}  = \left( {2 - t;\,\, - 1 - t} \right)\).

Theo đề bài, ta có: \(MB = \sqrt 5 \)

\(\begin{array}{l} \Rightarrow M{B^2} = 5\\ \Leftrightarrow {\left( {2 - t} \right)^2} + {\left( { - 1 - t} \right)^2} = 5\\ \Leftrightarrow 2{t^2} - 2t = 0\\ \Leftrightarrow 2t\left( {t - 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}t = 0\\t - 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}t = 0\\t = 1\end{array} \right.\end{array}\)

+) Với \(t = 0 \Rightarrow M\left( {1;\,\,2} \right)\)

+) Với \(t = 1 \Rightarrow M\left( {2;\,\,3} \right)\)

Vậy \(M\left( {1;\,\,2} \right)\) hoặc \(M\left( {2;\,\,3} \right)\)thì \(M\) cách \(B\) một khoảng bằng \(\sqrt 5 \).

Câu 5 (VD) - Phương trình quy về phương trình bậc nhất, phương trình bậc hai

Phương pháp:

+ Tìm ĐKXĐ

+ Biến đổi phương trình đã cho về dạng \({\left( {2x - \sqrt {x + 3} } \right)^2} + {\left( {\sqrt {2x - 1}  - 1} \right)^2} = 0\).

Cách giải:

ĐKXĐ:\(\left\{ \begin{array}{l}x + 3 \ge 0\\2x - 1 \ge 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x \ge  - 3\\x \ge \dfrac{1}{2}\end{array} \right.\)\( \Leftrightarrow x \ge \dfrac{1}{2}\)

\(\begin{array}{l}\,\,4x\sqrt {x + 3}  + 2\sqrt {2x - 1} \\ = 4{x^2} + 3x + 3\\ \Leftrightarrow 4{x^2} - 2.2x.\sqrt {x + 3}  + {\left( {\sqrt {x + 3} } \right)^2}\\ - x - 3 - 2\sqrt {2x - 1}  + 3x + 3 = 0\\ \Leftrightarrow 4{x^2} - 2.2x.\sqrt {x + 3}  + {\left( {\sqrt {x + 3} } \right)^2} \\+ 2x - 2\sqrt {2x - 1}  = 0\\ \Leftrightarrow 4{x^2} - 2.2x.\sqrt {x + 3}  + {\left( {\sqrt {x + 3} } \right)^2} \\+ 2x - 1 - 2\sqrt {2x - 1}  + 1 = 0\\ \Leftrightarrow 4{x^2} - 2.2x.\sqrt {x + 3}  + {\left( {\sqrt {x + 3} } \right)^2}\\ + {\left( {\sqrt {2x - 1} } \right)^2} - 2.1.\sqrt {2x - 1}  + 1 = 0\\ \Leftrightarrow {\left( {2x - \sqrt {x + 3} } \right)^2} + {\left( {\sqrt {2x - 1}  - 1} \right)^2} = 0\end{array}\)

Ta có:

\(\left. \begin{array}{l}{\left( {2x - \sqrt {x + 3} } \right)^2} \ge 0\\{\left( {\sqrt {2x - 1}  - 1} \right)^2} \ge 0\end{array} \right\}\)\( \Rightarrow {\left( {2x - \sqrt {x + 3} } \right)^2} + {\left( {\sqrt {2x - 1}  - 1} \right)^2} \ge 0\)

Dấu “\( = \)” xảy ra khi và chỉ khi:

 \(\begin{array}{l}\,\left\{ \begin{array}{l}2x - \sqrt {x + 3}  = 0\\\sqrt {2x - 1}  - 1 = 0\end{array} \right. \\\Leftrightarrow \left\{ \begin{array}{l}{\left( {2x} \right)^2} = {\left( {\sqrt {x + 3} } \right)^2}\\{\left( {\sqrt {2x - 1} } \right)^2} = 1\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}4{x^2} - x - 3 = 0\\2x = 2\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}x = 1\\x =  - \dfrac{3}{4}\end{array} \right.\\x = 1\end{array} \right.\\ \Leftrightarrow x = 1\,\left( {tm} \right)\end{array}\)

Vậy phương trình có nghiệm \(x = 1\).

Loigiaihay.com