 Giải toán 10, giải bài tập toán lớp 10 đầy đủ đại số và hình học
Giải toán 10, giải bài tập toán lớp 10 đầy đủ đại số và hình học
 Đề ôn tập giữa kì 2- Có đáp án và lời giải
Đề ôn tập giữa kì 2- Có đáp án và lời giải
Đề kiểm tra giữa kì 2 Toán 10 - đề số 6 có lời giải chi tiết
Đáp án và lời giải chi tiết Đề kiểm tra giữa kì 2 Toán 10
Đề bài
Câu 1 (5,0 điểm): Giải các bất phương trình sau:
a) \(\dfrac{{{x^2} - 5x + 6}}{{5 - {x^2}}} \ge 0\)
b) \(\dfrac{1}{{x - 2}} - \dfrac{1}{{x - 1}} < 0\)
c) \({\left( {\left| {x - 3} \right| - 1} \right)^2} > {x^2}\)
Câu 2 (1,5 điểm): Tìm \(m\) để bất phương trình \({x^2} - 2\left( {m - \dfrac{2}{3}} \right)x - m + \dfrac{{20}}{3} \ge 0\) có nghiệm tùy ý.
Câu 3 (2,0 điểm): Giải hệ bất phương trình: \(\left\{ \begin{array}{l}\dfrac{{2 - 3x}}{{4x - 1}} \le 0\\{\left( {x + 1} \right)^2} - 16 > 0\end{array} \right.\).
Câu 4 (1,5 điểm): Tìm \(m\) để phương trình \(m{x^2} - 2\left( {m + 1} \right)x + 2 = 0\) có nghiệm âm.
Lời giải chi tiết
Câu 1 (VD) - Bất phương trình
Phương pháp:
a) Tìm ĐKXĐ. Lập bảng xét dấu để tìm tập nghiệm của bất phương trình.
b) Quy đồng và áp dụng: Nếu \(\dfrac{a}{b} < 0\) và \(a > 0\) thì \(b < 0\).
c) Phá dấu giá trị tuyệt đối, giải các bất phương trình nhận được và kết luận tập nhiệm: \(\left| a \right| = \left\{ \begin{array}{l}a\,\,{\mathop{\rm khi}\nolimits} \,\,a \ge 0\\ - a\,\,{\mathop{\rm khi}\nolimits} \,\,a < 0\end{array} \right.\)
Cách giải:
Giải các bất phương trình sau:
a) \(\dfrac{{{x^2} - 5x + 6}}{{5 - {x^2}}} \ge 0\)
\(\dfrac{{{x^2} - 5x + 6}}{{5 - {x^2}}} \ge 0\)
ĐKXĐ: \(5 - {x^2} \ne 0 \Leftrightarrow x \ne \pm \sqrt 5 \)
Ta có bảng xét dấu:
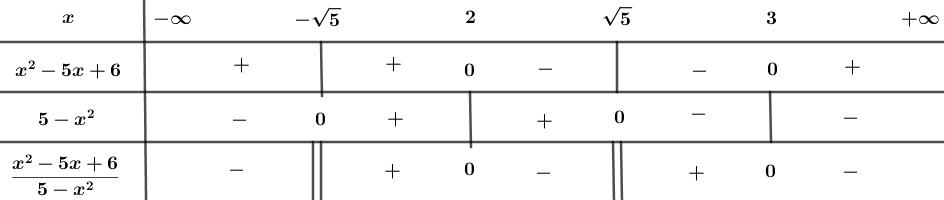
Để \(\dfrac{{{x^2} - 5x + 6}}{{5 - {x^2}}} \ge 0\) thì \(x \in \left( { - \sqrt 5 ;\,\,2} \right] \cup \left( {\sqrt 5 ;\,\,3} \right]\)
Vậy bất phương trình có tập nghiệm \(S = \left( { - \sqrt 5 ;\,\,2} \right] \cup \left( {\sqrt 5 ;\,\,3} \right]\).
b) \(\dfrac{1}{{x - 2}} - \dfrac{1}{{x - 1}} < 0\)
\(\dfrac{1}{{x - 2}} - \dfrac{1}{{x - 1}} < 0\) ĐKXĐ: \(x \ne 1;\,\,x \ne 2\)
\(\begin{array}{l} \Leftrightarrow \dfrac{{\left( {x - 1} \right) - \left( {x - 2} \right)}}{{\left( {x - 1} \right).\left( {x - 2} \right)}} < 0\\ \Leftrightarrow \dfrac{{x - 1 - x + 2}}{{\left( {x - 1} \right).\left( {x - 2} \right)}} < 0\\ \Leftrightarrow \dfrac{1}{{\left( {x - 1} \right).\left( {x - 2} \right)}} < 0\end{array}\)
\(\begin{array}{l} \Leftrightarrow \left( {x - 1} \right).\left( {x - 2} \right) < 0\,\,\,\left( {{\rm{vì }}\,\,1 > 0} \right)\\ \Leftrightarrow 1 < x < 2\end{array}\)
Vậy bất phương trình có tập nghiệm \(S = \left( {1;\,\,2} \right)\).
c) \({\left( {\left| {x - 3} \right| - 1} \right)^2} > {x^2}\)
TH1: \(x - 3 \ge 0 \Leftrightarrow x \ge 3\)
Bất phương trình \( \Leftrightarrow {\left( {x - 4} \right)^2} > {x^2}\)
\( \Leftrightarrow {x^2} - 8x + 16 > {x^2}\)
\( \Leftrightarrow - 8x + 16 > 0\)
\( \Leftrightarrow x < 2\)
Mà \(x \ge 3 \Rightarrow x \in \left\{ \emptyset \right\}\).
TH2: \(x - 3 < 0 \Leftrightarrow x < 3\)
Bất phương trình \( \Leftrightarrow {\left( {2 - x} \right)^2} > {x^2}\)
\( \Leftrightarrow 4 - 4x + {x^2} > {x^2}\)
\( \Leftrightarrow 4 - 4x > 0\)
\( \Leftrightarrow x < 1\)
Mà \(x < 3 \Rightarrow x < 1\).
Kết hợp cả hai trường hợp ta được tập nghiệm của bất phương trình là: \(S = \left( { - \infty ;\,\,1} \right)\)
Câu 2 (VD) - Bất phương trình
Phương pháp:
Áp dụng: \(f\left( x \right) = {a^2}x + bx + c \ge 0,\,\,\forall x \in \mathbb{R}\)\( \Leftrightarrow \left\{ \begin{array}{l}a > 0\\\Delta \le 0\end{array} \right.\)
Cách giải:
Tìm \(m\) để bất phương trình \({x^2} - 2\left( {m - \dfrac{2}{3}} \right)x - m + \dfrac{{20}}{3} \ge 0\) có nghiệm tùy ý.
Bất phương trình \({x^2} - 2\left( {m - \dfrac{2}{3}} \right)x - m + \dfrac{{20}}{3} \ge 0\) có nghiệm tùy ý khi và chỉ khi \(\left\{ \begin{array}{l}a > 0\\\Delta \le 0\end{array} \right.\).
+) \(a = 1 > 0\) luôn đúng
+) \(\Delta \le 0\)
\(\begin{array}{l}\Delta \le 0 \Leftrightarrow 4{\left( {m - \dfrac{2}{3}} \right)^2} - 4.1.\left( { - m + \dfrac{{20}}{3}} \right) \le 0\\\, \Leftrightarrow 4\left( {{m^2} - \dfrac{4}{3}m + \dfrac{4}{9}} \right) + 4m - \dfrac{{80}}{3} \le 0\\\, \Leftrightarrow 4{m^2} - \dfrac{{16}}{3}m + \dfrac{{16}}{9} + 4m - \dfrac{{80}}{3} \le 0\\\, \Leftrightarrow 4{m^2} - \dfrac{4}{3}m - \dfrac{{224}}{9} \le 0\\\, \Leftrightarrow - \dfrac{7}{3} \le m \le \dfrac{8}{3}\end{array}\)
Vậy \( - \dfrac{7}{3} \le m \le \dfrac{8}{3}\).
Câu 3 (VD) - Bất phương trình và hệ bất phương trình một ẩn
Phương pháp:
Giải từng bất phương trình sau đó kết hợp nghiệm.
Cách giải:
Giải hệ bất phương trình: \(\left\{ \begin{array}{l}\dfrac{{2 - 3x}}{{4x - 1}} \le 0\\{\left( {x + 1} \right)^2} - 16 > 0\end{array} \right.\).
\(\left\{ \begin{array}{l}\dfrac{{2 - 3x}}{{4x - 1}} \le 0\\{\left( {x + 1} \right)^2} - 16 > 0\end{array} \right.\)
ĐKXĐ: \(4x - 1 \ne 0 \Leftrightarrow x \ne \dfrac{1}{4}\)
\( \Leftrightarrow \left\{ \begin{array}{l}\dfrac{{2 - 3x}}{{4x - 1}} \le 0\\{x^2} + 2x + 1 - 16 > 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}\dfrac{{2 - 3x}}{{4x - 1}} \le 0\\{x^2} + 2x - 15 > 0\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}\left\{ \begin{array}{l}2 - 3x \ge 0\\4x - 1 < 0\end{array} \right.\\\left\{ \begin{array}{l}2 - 3x \le 0\\4x - 1 > 0\end{array} \right.\end{array} \right.\\\left[ \begin{array}{l}x < - 5\\x > 3\end{array} \right.\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}x < \dfrac{1}{4}\\x \ge \dfrac{2}{3}\end{array} \right.\\\left[ \begin{array}{l}x < - 5\\x > 3\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x < - 5\\x > 3\end{array} \right.\)
Vậy hệ bất phương trình có tập nghiệm \(S = \left( { - \infty ;\,\, - 5} \right) \cup \left( {3;\,\, + \infty } \right)\).
Câu 4 (VDC) - Phương trình quy về phương trình bậc hai
Phương pháp:
Xác định điều kiện của \(m\) để phương trình có hai nghiệm trái dấu và hai nghiệm âm.
Cách giải:
Tìm \(m\) để phương trình \(m{x^2} - 2\left( {m + 1} \right)x + 2 = 0\,\,\,\left( 1 \right)\) có nghiệm âm.
+) \(m = 0\): PT \(\left( 1 \right)\) trở thành: \( - 2x + 2 = 0\)\( \Leftrightarrow x = 1 > 0\) (không thỏa mãn)
+) \(m \ne 0\)
\(\Delta = 4{\left( {m + 1} \right)^2} - 4.m.2\)\( = 4{m^2} + 4 > 0\) với mọi \(m\)
\( \Rightarrow \) Phương trình \(\left( 1 \right)\) có hai nghiệm phân biệt với \(m \ne 0\).
PT \(\left( 1 \right)\) có \(1\) nghiệm âm \( \Leftrightarrow \)PT \(\left( 1 \right)\) có hai nghiệm trái dấu \( \Leftrightarrow \)\(ac < 0 \Leftrightarrow 2m < 0\)\( \Leftrightarrow m < 0\).
PT \(\left( 1 \right)\) có \(2\) nghiệm âm \( \Leftrightarrow \left\{ \begin{array}{l}P > 0\\S < 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}\dfrac{2}{m} > 0\\\dfrac{{2\left( {m + 1} \right)}}{m} < 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}m > 0\\ - 1 < m < 0\end{array} \right.\,\,\,\left( {ktm} \right)\)
Vậy \(m < 0\) thì phương trình \(\left( 1 \right)\) có nghiệm âm.
Loigiaihay.com
- Đề kiểm tra giữa kì 2 Toán 10 - đề số 7 có lời giải chi tiết
- Đề kiểm tra giữa kì 2 Toán 10 - đề số 5 có lời giải chi tiết
- Đề kiểm tra giữa kì 2 Toán 10 - đề số 4 có lời giải chi tiết
- Đề kiểm tra giữa kì 2 Toán 10 - đề số 3 có lời giải chi tiết
- Đề kiểm tra giữa kì 2 Toán 10 - đề số 2 có lời giải chi tiết
>> Xem thêm












Danh sách bình luận