Giải toán 7, giải bài tập toán lớp 7 sgk đầy đủ đại số và hình học
Bài 5. Tính chất tia phân giác của một góc
Đề kiểm tra 15 phút - Đề số 4 - Bài 5, 6 - Chương 3 – Hình học 7
Giải Đề kiểm tra 15 phút - Đề số 4 - Bài 5, 6 - Chương 3 – Hình học 7
Đề bài
Cho tam giác ABC có \(\widehat A = {120^0}\); các phân giác AD, BE, CF.
a) Chứng minh rằng DE là tia phân giác góc ngoài của \(\Delta AB{\rm{D}}{\rm{.}}\)
b) Chứng minh \(\widehat {E{\rm{D}}F} = {90^0}.\)
Phương pháp giải - Xem chi tiết
+Tính chất tia phân giác của 1 góc
+Hai tia phân giác của hai góc kề bù thì vuông góc với nhau
Lời giải chi tiết
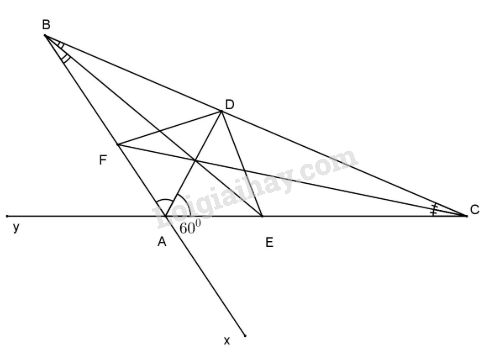
a) Ta có AD là tia phân giác của \(\widehat {BAC} = {120^0}.\)
\( \Rightarrow \widehat {BA{\rm{D}}} = \widehat {CA{\rm{D}}} = \dfrac{{\widehat {BAC}} }{ 2} = \dfrac{{{{120}^0}} }{ 2}\)\(\, = {60^0}.\)
Gọi Ax là tia đối của tia AB, ta có \(\widehat {xAC} = {180^0} - \widehat {BAC} = {180^0} - {120^0} \)\(\,= {60^0}\)
Chứng tỏ AE là tia phân giác của góc \(\widehat {DAx}\);
Lại có E thuộc tia phân giác của góc \(\widehat {ABC} \Rightarrow E\) thuộc tia phân giác của góc \(\widehat {A{\rm{D}}C}\)
Hay DE là phân giác của góc ngoài ADB (theo Đề số 3)
b) Vẽ tia Ay là tia đối của tia AC.
Ta cũng có DF là phân giác góc ngoài của \(\Delta A{\rm{D}}C\), mà \(\widehat {B{\rm{D}}A}\) và \(\widehat {A{\rm{D}}C}\) là hai góc kề bù.
Do đó \(DF \bot DE\) (hai tia phân giác của hai góc kề bù thì vuông góc với nhau) hay \(\widehat {E{\rm{D}}F} = {90^0}.\)
Loigiaihay.com
Bình luận
Chia sẻ
- Đề kiểm tra 15 phút - Đề số 6 - Bài 5, 6 - Chương 3 – Hình học 7
- Đề kiểm tra 15 phút - Đề số 7 - Bài 5, 6 - Chương 3 – Hình học 7
- Đề kiểm tra 15 phút - Đề số 8 - Bài 5, 6 - Chương 3 – Hình học 7
- Đề kiểm tra 15 phút - Đề số 3 - Bài 5, 6 - Chương 3 – Hình học 7
- Đề kiểm tra 15 phút - Đề số 2 - Bài 5, 6 - Chương 3 – Hình học 7
>> Xem thêm
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
