-
Đề kiểm tra 15 phút
-
Đề kiểm tra 15 phút - Chương I - Giải Tích 12
-
Đề kiểm tra 15 phút - Chương II - Giải Tích 12
-
Đề kiểm tra 15 phút - Chương III - Giải Tích 12
-
Đề kiểm tra 15 phút – Chương IV – Giải tích 12
-
Đề kiểm tra 15 phút - Chương I - Hình học 12
-
Đề kiểm tra 15 phút - Chương II - Hình học 12
-
Đề kiểm tra 15 phút - Chương III - Hình học 12
-
-
Đề kiểm tra 1 tiết
-
Đề kiểm tra 45 phút (1 tiết) - Chương I - Giải Tích 12
-
Đề kiểm tra 45 phút (1 tiết) - Chương II - Giải Tích 12
-
Đề kiểm tra 45 phút (1 tiết) - Chương III - Giải Tích 12
-
Đề kiểm tra 45 phút (1 tiết) - Chương IV - Giải Tích 12
-
Đề kiểm tra 45 phút (1 tiết) - Chương I - Hình học 12
-
Đề kiểm tra 45 phút (1 tiết) - Chương II - Hình học 12
-
Đề kiểm tra 45 phút (1 tiết) - Chương III - Hình học 12
-
-
Đề thi giữa học kì 1
-
Đề thi học kì 1
-
Đề thi giữa học kì 2
-
Đề thi học kì 2
-
ĐỀ THI THỬ THPT QUỐC GIA MÔN TOÁN
Đề kiểm tra 1 tiết Toán 12 chương 1: Hàm số - Đề số 2
Đề bài
Cho hàm số $y = a{x^4} + b{x^2} + c\left( {a > 0} \right)$. Chọn kết luận đúng:
-
A.
$\mathop {\lim }\limits_{x \to \pm \infty } y = - \infty $
-
B.
$\mathop {\lim }\limits_{x \to + \infty } y = + \infty $
-
C.
$\mathop {\lim }\limits_{x \to - \infty } y = - \infty $
-
D.
$\mathop {\lim }\limits_{x \to \pm \infty } y = 0$
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên
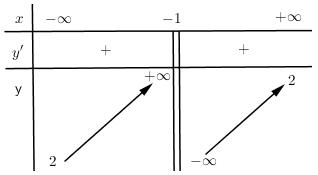
Tiệm cận đứng và tiệm cận ngang của đồ thị hàm số cắt nhau tại điểm có tọa độ là:
-
A.
$\left( {1;\, - 2} \right)$
-
B.
$\left( { - 1;\,2} \right)$
-
C.
$\left( {1;\,2} \right)$
-
D.
$\left( { - 1;\,1} \right)$
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
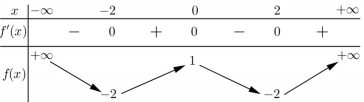
Số nghiệm thực của phương trình \(2f\left( x \right) + 3 = 0\) là:
-
A.
\(4\)
-
B.
\(3\)
-
C.
\(2\)
-
D.
\(1\)
Đường cong ở hình bên là đồ thị hàm số \(y=\dfrac{ax+2}{cx+b}\) với \(a,b,c\) là các số thực. Mệnh đề nào sau đây đúng?
-
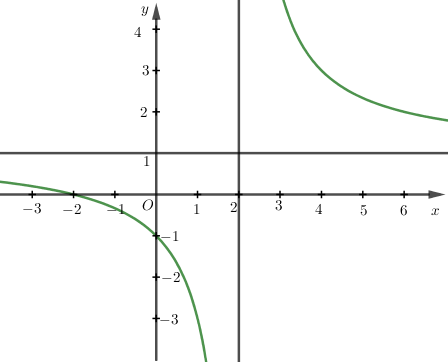
A.
\(a=2;b=2;c=-1\).
-
B.
\(a=1;b=-2;c=1\).
-
C.
\(a=1;b=2;c=1\).
-
D.
\(a=1;b=1;c=-1\).
Cho hàm số \(f\left( x \right)\) có đạo hàm trên \(R\). Nếu hàm số \(f\left( x \right)\) nghịch biến trên \(R\) thì:
-
A.
$f'\left( x \right) \ge 0,\forall x \in R.$
-
B.
$f'\left( x \right) = 0,\forall x \in R$
-
C.
$f'\left( x \right) < 0,\forall x \in R.$
-
D.
$f'\left( x \right) \le 0,\forall x \in R.$
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = 1,\,\,\forall x \in \mathbb{R}\). Mệnh đề nào sau đây đúng?
-
A.
\(f\left( { - 1} \right) > f\left( 2 \right)\)
-
B.
\(f\left( { - 1} \right) < f\left( 2 \right)\)
-
C.
\(f\left( { - 1} \right) = f\left( 2 \right)\)
-
D.
\(f\left( { - 1} \right) \ge f\left( 2 \right)\)
Cho biết GTLN của hàm số $f\left( x \right)$ trên $\left[ {1;3} \right]$ là $M = - 2$. Chọn khẳng định đúng:
-
A.
$f\left( x \right) \geqslant - 2,\forall x \in \left[ {1;3} \right]$
-
B.
$f\left( 1 \right) = f\left( 3 \right) = - 2$
-
C.
$f\left( x \right) < - 2,\forall x \in \left[ {1;3} \right]$
-
D.
$f\left( x \right) \leqslant - 2,\forall x \in \left[ {1;3} \right]$
Giá trị lớn nhất của hàm số $f\left( x \right) = \dfrac{{\sin x}}{x}$ trên đoạn $\left[ {\dfrac{\pi }{6};\dfrac{\pi }{3}} \right]$ là:
-
A.
$\dfrac{\pi }{{\sqrt 3 }}$
-
B.
$\dfrac{3}{\pi }$
-
C.
$\dfrac{\pi }{2}$
-
D.
$\dfrac{2}{\pi }$
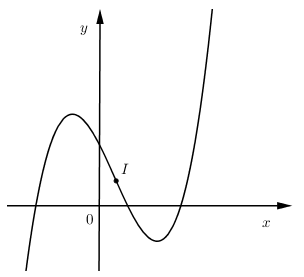
Hàm số $y = f\left( x \right) = a{x^3} + b{x^2} + cx + d$ có đồ thị như hình vẽ, chọn kết luận đúng:
-
A.
$a > 0$
-
B.
$a < 0$
-
C.
$a = 0$
-
D.
$a \leqslant 0$
Hệ số góc của tiếp tuyến của đồ thị hàm số $y = \dfrac{{{x^4}}}{4} + \dfrac{{{x^2}}}{2} - 1$ tại điểm có hoành độ $x = - 1$ là:
-
A.
$0$
-
B.
$2$
-
C.
$ - 2$
-
D.
$3$
Hàm số \(y = - {x^3} + {x^2} + 1\,\) xác định khi:
-
A.
\(x \ne 0\)
-
B.
\(x \in \mathbb{Z}\)
-
C.
\(\forall x\)
-
D.
\(x > 0\)
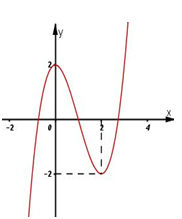
Cho hàm số y = f (x) có đồ thị như hình bên. Mệnh đề nào dưới đây đúng?
-
A.
Hàm số có giá trị cực tiểu bằng 2
-
B.
Hàm số đạt cực đại tại x = 0 và đạt cực tiểu tại x = 2.
-
C.
Hàm số có giá trị lớn nhất bằng 2 và giá trị nhỏ nhất bằng -2.
-
D.
Hàm số có ba điểm cực trị
Tìm tất cả các giá trị của $m$ để hàm số $y = - \dfrac{1}{3}{x^3} + \dfrac{{m{x^2}}}{3} + 4$ đạt cực đại tại $x = 2?$
-
A.
$m = 1$
-
B.
$m = 2$
-
C.
$m = 3$
-
D.
$m = 4$
Tiệm cận ngang của đồ thị hàm số:
-
A.
vuông góc với trục hoành
-
B.
vuông góc với trục tung.
-
C.
nằm bên trái trục tung
-
D.
nằm phía trên trục hoành
Hàm số nào dưới đây không có cực trị?
-
A.
\(y = \dfrac{{x - 2}}{{x + 1}}\)
-
B.
\(y = {x^2}\)
-
C.
\(y = {x^3} - 3x\)
-
D.
\(y = - {x^4}\)
Gọi $m$ là giá trị nhỏ nhất của hàm số $y = x - 1 + \dfrac{4}{{x - 1}}$ trên khoảng $\left( {1; + \infty {\rm{\;}}} \right)$. Tìm $m?$
-
A.
$m = 2$
-
B.
$m = 5$
-
C.
$m = 3$
-
D.
$m = 4$
Tìm tất cả các giá trị thực của tham số $m$ để hàm số $y = mx - \sin x$ đồng biến trên $\mathbb{R}.$
-
A.
$m > 1.$
-
B.
$m \le - 1.$
-
C.
$m \ge 1.$
-
D.
$m \ge - 1.$
Tìm $m$ để $({C_m})$ : $y = {x^4} - 2m{x^2} + 2$ có $3$ điểm cực trị là $3$ đỉnh của một tam giác vuông cân.
-
A.
$m = - 4$
-
B.
$m = - 1$
-
C.
$m = 1$
-
D.
$m = 3$
Biết rằng hàm số \(y = a{x^3} + b{x^2} + cx + d\,\,\left( {a\not = 0} \right)\) có đồ thị là một trong các dạng dưới đây:
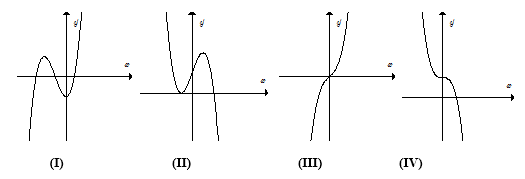
Mệnh đề nào sau đây là đúng?
-
A.
Đồ thị (I) xảy ra khi \(a < 0\) và \(f'\left( x \right) = 0\) có hai nghiệm phân biệt.
-
B.
Đồ thị (II) xảy ra khi \(a > 0\) và \(f'\left( x \right) = 0\) có hai nghiệm phân biệt
-
C.
Đồ thị (III) xảy ra khi \(a > 0\) và \(f'\left( x \right) = 0\) vô nghiệm hoặc có nghiệm kép.
-
D.
Đồ thị (IV) xảy ra khi \(a > 0\) và \(f'\left( x \right) = 0\) có có nghiệm kép.
Cho hàm số \(y = \dfrac{{2x + b}}{{cx + d}}\) có bảng biến thiên:
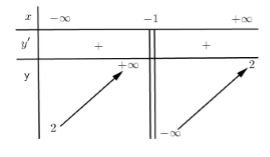
Giá trị của \(2{c^2} - 5{d^2}\) bằng
-
A.
$-3$
-
B.
$0$
-
C.
$2$
-
D.
$4$
Cho hàm số \(y = {x^3} + 2m{x^2} + \left( {m + 3} \right)x + 4\,\,\,\left( {{C_m}} \right)\). Giá trị của tham số \(m\) để đường thẳng \(\left( d \right):y = x + 4\) cắt \(\left( {{C_m}} \right)\) tại ba điểm phân biệt \(A\left( {0;4} \right),\,\,B,\,\,C\) sao cho tam giác \(KBC\) có diện tích bằng \(8\sqrt 2 \) với điểm \(K\left( {1;3} \right)\) là:
-
A.
\(m = \frac{{1 - \sqrt {137} }}{2}\)
-
B.
\(m = \frac{{1 + \sqrt {137} }}{2}\)
-
C.
\(m = \frac{{1 \pm \sqrt {137} }}{2}\)
-
D.
\(m = \frac{{ \pm 1 + \sqrt {137} }}{2}\)
Tiếp tuyến của đồ thị hàm số $y = \dfrac{{{x^3}}}{3} - 2{x^2} + x + 2$ song song với đường thẳng $y = - 2x + 5$ có phương trình là:
-
A.
$2x + y - \dfrac{{10}}{3} = 0$ và $2x + y - 2 = 0$
-
B.
$2x + y + \dfrac{4}{3} = 0$ và $2x + y + 2 = 0$
-
C.
$2x + y - 4 = 0$ và $2x + y - 1 = 0$
-
D.
$y = 2x + y - 3 = 0$ và $2x + y + 1 = 0$
Cho hàm số \(f\left( x \right) = a{x^4} + b{x^3} + c{x^2} + dx + e,\) với \(a,b,c,d,e \in \mathbb{R}.\) Hàm số \(y = f'\left( x \right)\) có đồ thị như hình vẽ. Trong các khẳng định sau, khẳng định nào đúng?
-
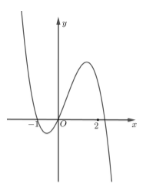
A.
\(a + b + c + d < 0\)
-
B.
\(a + c < b + d\)
-
C.
\(a + c > 0\)
-
D.
\(d + b - c > 0\)
Cho hai số thực \(x,\,y\) thỏa mãn \({x^2} + {y^2} - 4x + 6y + 4 + \sqrt {{y^2} + 6y + 10} = \sqrt {6 + 4x - {x^2}} \). Gọi \(M,\,m\) lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức \(T = \left| {\sqrt {{x^2} + {y^2}} - a} \right|\). Có bao nhiêu giá trị nguyên thuộc đoạn \(\left[ { - 10;\,10} \right]\) của tham số \(a\) để \(M \ge 2m\)?
-
A.
\(17\).
-
B.
\(16\).
-
C.
\(15\).
-
D.
\(18\).
Cho hàm số \(y = f\left( x \right) = {2^{2019}}{x^3} + {3.2^{2018}}{x^2} - 2018\) có đồ thị cắt trục hoành tại ba điểm phân biệt có hoành độ \({x_1};{x_2};{x_3}\). Tính giá trị biểu thức \(P = \dfrac{1}{{f'\left( {{x_1}} \right)}} + \dfrac{1}{{f'\left( {{x_2}} \right)}} + \dfrac{1}{{f'\left( {{x_3}} \right)}}.\)
-
A.
\(P = {3.2^{2018}}\)
-
B.
\(P = - 2018\)
-
C.
\(P = 0\)
-
D.
\(P = {2^{2019}}\)
Lời giải và đáp án
Cho hàm số $y = a{x^4} + b{x^2} + c\left( {a > 0} \right)$. Chọn kết luận đúng:
-
A.
$\mathop {\lim }\limits_{x \to \pm \infty } y = - \infty $
-
B.
$\mathop {\lim }\limits_{x \to + \infty } y = + \infty $
-
C.
$\mathop {\lim }\limits_{x \to - \infty } y = - \infty $
-
D.
$\mathop {\lim }\limits_{x \to \pm \infty } y = 0$
Đáp án : B
Vì $a > 0$ nên $\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to - \infty } y = + \infty $.
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên
Tiệm cận đứng và tiệm cận ngang của đồ thị hàm số cắt nhau tại điểm có tọa độ là:
-
A.
$\left( {1;\, - 2} \right)$
-
B.
$\left( { - 1;\,2} \right)$
-
C.
$\left( {1;\,2} \right)$
-
D.
$\left( { - 1;\,1} \right)$
Đáp án : B
Tìm các đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số rồi tìm giao điểm của chúng.
Từ bảng biến thiên ta có:
- Tiệm cận đứng của đồ thị hàm số là $x = - 1.$
- Tiệm cận ngang của đồ thị hàm số là $y = 2.$
Vậy tiệm cận đứng và tiệm cận ngang của đồ thị hàm số cắt nhau tại điểm có tọa độ là $\left( { - 1;2} \right)$
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
Số nghiệm thực của phương trình \(2f\left( x \right) + 3 = 0\) là:
-
A.
\(4\)
-
B.
\(3\)
-
C.
\(2\)
-
D.
\(1\)
Đáp án : A
+) Số nghiệm của phương trình \(f\left( x \right) = m\) là số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = m.\)
+) Dựa vào BBT để xác định số giao điểm của các đồ thị hàm số.
Ta có: \(Pt \Leftrightarrow 2f\left( x \right) = - 3 \Leftrightarrow f\left( x \right) = - \dfrac{3}{2}.\;\;\left( * \right)\)
Số nghiệm của phương trình \(\left( * \right)\) là số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = - \dfrac{3}{2}.\)
Dựa vào BBT ta thấy đường thẳng \(y = - \dfrac{3}{2}\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại 4 điểm phân biệt.
\( \Rightarrow Pt\;\;\left( * \right)\) có 4 nghiệm phân biệt.
Đường cong ở hình bên là đồ thị hàm số \(y=\dfrac{ax+2}{cx+b}\) với \(a,b,c\) là các số thực. Mệnh đề nào sau đây đúng?
-
A.
\(a=2;b=2;c=-1\).
-
B.
\(a=1;b=-2;c=1\).
-
C.
\(a=1;b=2;c=1\).
-
D.
\(a=1;b=1;c=-1\).
Đáp án : B
Sử dụng kiến thức về tiệm cận và giao của đồ thị hàm số với các trục tọa độ
Vì đồ thị hàm số nhận đường thẳng \(y=1;x=2\) làm đường tiệm cận ngang và tiệm cận đứng và đồ thị hàm số cắt \(Oy\) tại điểm có tung độ bằng \(-1\) nên ta có hệ :
\(\left\{ {\begin{array}{*{20}{c}}{ - \dfrac{b}{c} = 2}\\{\dfrac{a}{c} = 1}\\{\dfrac{2}{b} = - 1}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = 1}\\{b = - 2}\\{c = 1}\end{array}} \right.\).
Cho hàm số \(f\left( x \right)\) có đạo hàm trên \(R\). Nếu hàm số \(f\left( x \right)\) nghịch biến trên \(R\) thì:
-
A.
$f'\left( x \right) \ge 0,\forall x \in R.$
-
B.
$f'\left( x \right) = 0,\forall x \in R$
-
C.
$f'\left( x \right) < 0,\forall x \in R.$
-
D.
$f'\left( x \right) \le 0,\forall x \in R.$
Đáp án : D
Sử dụng tính chất: Hàm số \(f\left( x \right)\) nghịch biến trên \(\left( {a;b} \right)\) thì \(f'\left( x \right) \le 0,\forall x \in \left( {a;b} \right)\).
Lưu ý: Đạo hàm \(f'(x)\) có thể bằng 0 tại một số điểm và không ảnh hưởng đến tính đồng biến nghịch biến.
Hàm số \(y = f\left( x \right)\) nghịch biến trên \(R\) thì \(f'\left( x \right) \le 0,\forall x \in R\).
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = 1,\,\,\forall x \in \mathbb{R}\). Mệnh đề nào sau đây đúng?
-
A.
\(f\left( { - 1} \right) > f\left( 2 \right)\)
-
B.
\(f\left( { - 1} \right) < f\left( 2 \right)\)
-
C.
\(f\left( { - 1} \right) = f\left( 2 \right)\)
-
D.
\(f\left( { - 1} \right) \ge f\left( 2 \right)\)
Đáp án : B
Hàm số có \(f'\left( x \right) > 0\) trên \(\mathbb{R}\) thì hàm số đó đồng biến trên \(\mathbb{R}.\)
Ta có: \(f'\left( x \right) = 1 > 0\,\,\forall x \in \mathbb{R} \Rightarrow \) Hàm số đồng biến trên \(\mathbb{R}.\)
Ta có: \( - 1 < 2 \Rightarrow f\left( { - 1} \right) < f\left( 2 \right)\)
Cho biết GTLN của hàm số $f\left( x \right)$ trên $\left[ {1;3} \right]$ là $M = - 2$. Chọn khẳng định đúng:
-
A.
$f\left( x \right) \geqslant - 2,\forall x \in \left[ {1;3} \right]$
-
B.
$f\left( 1 \right) = f\left( 3 \right) = - 2$
-
C.
$f\left( x \right) < - 2,\forall x \in \left[ {1;3} \right]$
-
D.
$f\left( x \right) \leqslant - 2,\forall x \in \left[ {1;3} \right]$
Đáp án : D
Nếu $M = - 2$ là GTLN của hàm số $y = f\left( x \right)$ trên $\left[ {1;3} \right]$ thì $f\left( x \right) \leqslant - 2,\forall x \in \left[ {1;3} \right]$.
Giá trị lớn nhất của hàm số $f\left( x \right) = \dfrac{{\sin x}}{x}$ trên đoạn $\left[ {\dfrac{\pi }{6};\dfrac{\pi }{3}} \right]$ là:
-
A.
$\dfrac{\pi }{{\sqrt 3 }}$
-
B.
$\dfrac{3}{\pi }$
-
C.
$\dfrac{\pi }{2}$
-
D.
$\dfrac{2}{\pi }$
Đáp án : B
Sử dụng phương pháp tìm GTLN, GTNN của hàm số:
- Tính \(y'\) và tìm các nghiệm của \(y' = 0\).
- Tính giá trị hàm số tại các điểm đặc biệt và kết luận.
TXĐ: $x \ne 0$.
$f'\left( x \right) = \dfrac{{x\cos x - \sin x}}{{{x^2}}} < 0 \forall x \in \left[ {\dfrac{\pi }{6};\dfrac{\pi }{3}} \right]$
Thật vậy,
Xét hàm \(g\left( x \right) = x\cos x - \sin x\) trên \(\left[ {\dfrac{\pi }{6};\dfrac{\pi }{3}} \right]\) có:
\(g'\left( x \right) = \cos x - x\sin x - \cos x\) \( = - x\sin x < 0,\forall x \in \left[ {\dfrac{\pi }{6};\dfrac{\pi }{3}} \right]\)
Do đó hàm số \(g\left( x \right)\) nghịch biến trên \(\left[ {\dfrac{\pi }{6};\dfrac{\pi }{3}} \right]\).
Suy ra \(g\left( x \right) \le g\left( {\dfrac{\pi }{6}} \right)\) \( = \dfrac{\pi }{6}.\cos \dfrac{\pi }{6} - \sin \dfrac{\pi }{6} < 0\) hay \(x\cos x - \sin x < 0\) với \(\forall x \in \left[ {\dfrac{\pi }{6};\dfrac{\pi }{3}} \right]\)
$ \Rightarrow \mathop {\max }\limits_{\left[ {\dfrac{\pi }{6};\dfrac{\pi }{3}} \right]} f\left( x \right) = f\left( {\dfrac{\pi }{6}} \right) = \dfrac{3}{\pi }$.
Hàm số $y = f\left( x \right) = a{x^3} + b{x^2} + cx + d$ có đồ thị như hình vẽ, chọn kết luận đúng:
-
A.
$a > 0$
-
B.
$a < 0$
-
C.
$a = 0$
-
D.
$a \leqslant 0$
Đáp án : A
Quan sát đồ thị ta thấy $\mathop {\lim }\limits_{x \to + \infty } y = + \infty ;\mathop {\lim }\limits_{x \to - \infty } y = - \infty $ nên $a > 0$.
Hệ số góc của tiếp tuyến của đồ thị hàm số $y = \dfrac{{{x^4}}}{4} + \dfrac{{{x^2}}}{2} - 1$ tại điểm có hoành độ $x = - 1$ là:
-
A.
$0$
-
B.
$2$
-
C.
$ - 2$
-
D.
$3$
Đáp án : C
Hệ số góc của tiếp tuyến của đồ thị hàm số $y = f\left( x \right)$ tại điểm có hoành độ $x = {x_0}$ là $k = f'\left( {{x_0}} \right)$.
Ta có $y' = {x^3} + x$
$ \Rightarrow $ Hệ số góc của tiếp tuyến với đồ thị hàm số tại điểm có hoành độ $x=-1$ là $k = y'( - 1) = - 2$
Hàm số \(y = - {x^3} + {x^2} + 1\,\) xác định khi:
-
A.
\(x \ne 0\)
-
B.
\(x \in \mathbb{Z}\)
-
C.
\(\forall x\)
-
D.
\(x > 0\)
Đáp án : C
Hàm đa thức bậc ba xác định trên tập số thực.
Hàm số \(y = - {x^3} + {x^2} + 1\,\) xác định với mọi \(x \in \mathbb{R}\)
Cho hàm số y = f (x) có đồ thị như hình bên. Mệnh đề nào dưới đây đúng?
-
A.
Hàm số có giá trị cực tiểu bằng 2
-
B.
Hàm số đạt cực đại tại x = 0 và đạt cực tiểu tại x = 2.
-
C.
Hàm số có giá trị lớn nhất bằng 2 và giá trị nhỏ nhất bằng -2.
-
D.
Hàm số có ba điểm cực trị
Đáp án : B
+) Dựa vào đồ thị hàm số để đưa ra các nhận xét đúng về đồ thị hàm số.
+) Hàm số đạt cực trị tại các điểm sao cho y’ = 0
Dựa vào đồ thị hàm số ta thấy hàm số có 2 điểm cực trị suy ra Loại đáp án D.
Hàm số đạt cực tiểu tại x = 2 và đạt cực đại tại x = 0. Suy ra Đáp án B đúng.
Tìm tất cả các giá trị của $m$ để hàm số $y = - \dfrac{1}{3}{x^3} + \dfrac{{m{x^2}}}{3} + 4$ đạt cực đại tại $x = 2?$
-
A.
$m = 1$
-
B.
$m = 2$
-
C.
$m = 3$
-
D.
$m = 4$
Đáp án : C
- Bước 1: Tính $y',y''$.
- Bước 2: Nêu điều kiện để $x = {x_0}$ là cực trị của hàm số:
+ $x = {x_0}$ là điểm cực đại nếu $\left\{ \begin{gathered} f'\left( {{x_0}} \right) = 0 \hfill \\f''\left( {{x_0}} \right) < 0 \hfill \\ \end{gathered} \right.$
+ $x = {x_0}$ là điểm cực tiểu nếu $\left\{ \begin{gathered}f'\left( {{x_0}} \right) = 0 \hfill \\ f''\left( {{x_0}} \right) > 0 \hfill \\ \end{gathered} \right.$
- Bước 3: Kết luận.
TXĐ $D = \mathbb{R}$
$y' = - {x^2} + \dfrac{2}{3}mx \Rightarrow y'' = - 2x + \dfrac{2}{3}m$
Hàm số đã cho đạt cực đại tại $x = 2$
$ \Leftrightarrow \left\{ \begin{gathered} y'(2) = 0 \hfill \\ y''\left( 2 \right) < 0 \hfill \\ \end{gathered} \right. $ $\Leftrightarrow \left\{ \begin{gathered} - {2^2} + \dfrac{2}{3}m.2 = 0 \hfill \\ - 2.2 + \dfrac{2}{3}m. < 0 \hfill \\ \end{gathered} \right. $ $\Leftrightarrow \left\{ \begin{gathered} - 4 + \dfrac{4}{3}m = 0 \hfill \\- 4 + \dfrac{2}{3}m < 0 \hfill \\ \end{gathered} \right. $ $\Leftrightarrow \left\{ \begin{gathered} m = 3 \hfill \\m < 6 \hfill \\ \end{gathered} \right. \Leftrightarrow m = 3$
Tiệm cận ngang của đồ thị hàm số:
-
A.
vuông góc với trục hoành
-
B.
vuông góc với trục tung.
-
C.
nằm bên trái trục tung
-
D.
nằm phía trên trục hoành
Đáp án : B
Phương trình đường tiệm cận ngang có dạng \(y = {y_0}\) nên nó vuông góc với đường thẳng \(x = 0\), hay vuông góc trục tung.
Hàm số nào dưới đây không có cực trị?
-
A.
\(y = \dfrac{{x - 2}}{{x + 1}}\)
-
B.
\(y = {x^2}\)
-
C.
\(y = {x^3} - 3x\)
-
D.
\(y = - {x^4}\)
Đáp án : A
Hàm phân thức bậc nhất trên bậc nhất \(y = \dfrac{{ax + b}}{{cx + d}}\) không có cực trị.
Dễ thấy hàm số \(y = \dfrac{{x - 2}}{{x + 1}}\) là hàm phân thức bậc nhất trên bậc nhất nên không có cực trị.
Ngoài ra, có thể kiểm tra được các cực trị của mỗi hàm số được cho ở ba đáp án B, C, D.
Gọi $m$ là giá trị nhỏ nhất của hàm số $y = x - 1 + \dfrac{4}{{x - 1}}$ trên khoảng $\left( {1; + \infty {\rm{\;}}} \right)$. Tìm $m?$
-
A.
$m = 2$
-
B.
$m = 5$
-
C.
$m = 3$
-
D.
$m = 4$
Đáp án : D
Sử dung BĐT Cauchy cho hai số không âm \(a + b \ge 2\sqrt {ab} \)
${\rm{\;}}x > 1 \Leftrightarrow x - 1 > 0$
$ \Rightarrow y = x - 1 + \dfrac{4}{{x - 1}} \ge 2\sqrt {\left( {x - 1} \right).\dfrac{4}{{x - 1}}} = 2.2 = 4$
Dấu bằng xảy ra $ \Leftrightarrow x - 1 = \dfrac{4}{{x - 1}} \Leftrightarrow {\left( {x - 1} \right)^2} = 4 \Leftrightarrow x = 3$.
Vậy GTNN của hàm số là $m=4$ khi $x=3$.
Tìm tất cả các giá trị thực của tham số $m$ để hàm số $y = mx - \sin x$ đồng biến trên $\mathbb{R}.$
-
A.
$m > 1.$
-
B.
$m \le - 1.$
-
C.
$m \ge 1.$
-
D.
$m \ge - 1.$
Đáp án : C
Sử dụng kết quả: hàm số $y = f\left( x \right)$ đồng biến trên tập $D$ nào đó khi và chỉ khi đạo hàm của hàm số trên tập $D$ không âm, tức là $f'\left( x \right) \ge 0,{\mkern 1mu} {\mkern 1mu} \forall x \in D.$
Áp dụng vào bài tập này ta đi tính đạo hàm $y'.$ Sau đó cho $y' \ge 0,{\mkern 1mu} {\mkern 1mu} \forall x \in \mathbb{R}$ để tìm giá trị của $m$
Để hàm số đã cho đồng biến trên $\mathbb{R}$ thì điều kiện cần và đủ là
$y' \ge 0 \Leftrightarrow {\left( {mx - \sin x} \right)^\prime } \ge 0 \Leftrightarrow m - \cos x \ge 0 \Leftrightarrow m \ge \cos x{\mkern 1mu} ,\forall x \in \mathbb{R}.$
Do $ - 1 \le \cos x \le 1,\forall x \in \mathbb{R},$ nên ta có $m \ge \cos x,{\mkern 1mu} \forall x \in \mathbb{R} \Leftrightarrow m \ge 1.$
Tìm $m$ để $({C_m})$ : $y = {x^4} - 2m{x^2} + 2$ có $3$ điểm cực trị là $3$ đỉnh của một tam giác vuông cân.
-
A.
$m = - 4$
-
B.
$m = - 1$
-
C.
$m = 1$
-
D.
$m = 3$
Đáp án : C
- Bước 1: Tính $y'$.
- Bước 2: Ba điểm cực trị $A,B,C$ trong đó $A\left( {0;c} \right)$ lập thành một tam giác vuông (vuông cân)
$ \Leftrightarrow \Delta ABC$ vuông tại $A \Leftrightarrow \overrightarrow {AB} .\overrightarrow {AC} = 0$
- Bước 3: Kết luận.
Ta có: $y' = 4{x^3} - 4mx = 0 \Leftrightarrow \left[ \begin{gathered} x = 0 \hfill \\ {x^2} = m \hfill \\ \end{gathered} \right.$
Đồ thị hàm số có $3$ điểm cực trị $ \Leftrightarrow $ pt $y' = 0$ có $3$ nghiệm phân biệt $ \Leftrightarrow $$m > 0$$ \Rightarrow \left[ \begin{gathered}x = 0 \hfill \\x = \sqrt m \hfill \\ x = - \sqrt m \hfill \\ \end{gathered} \right.$
$ \Rightarrow $ Đồ thị hàm số có $3$ điểm cực trị là: $A(0;2);\,\,\,B( - \sqrt m ;2 - {m^2});\,\,C(\sqrt m ;2 - {m^2})$
\(\overrightarrow {AB} = \left( { - \sqrt m ; - {m^2}} \right),\overrightarrow {AC} = \left( {\sqrt m ; - {m^2}} \right)\)
Dễ thấy $∆ ABC$ cân tại $A,$ để $∆ ABC$ vuông cân thì nó phải vuông tại $A$
\( \Rightarrow \overrightarrow {AB} .\overrightarrow {AC} = 0 \Leftrightarrow - m + {m^4} = 0\) \( \Leftrightarrow m\left( {{m^3} - 1} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}m = 0\\{m^3} - 1 = 0\end{array} \right.\) \( \Leftrightarrow \left[ \begin{array}{l}m = 0\\m = 1\end{array} \right.\)
Kết hợp điều kiện $m > 0$ ta có $m = 1$
Biết rằng hàm số \(y = a{x^3} + b{x^2} + cx + d\,\,\left( {a\not = 0} \right)\) có đồ thị là một trong các dạng dưới đây:
Mệnh đề nào sau đây là đúng?
-
A.
Đồ thị (I) xảy ra khi \(a < 0\) và \(f'\left( x \right) = 0\) có hai nghiệm phân biệt.
-
B.
Đồ thị (II) xảy ra khi \(a > 0\) và \(f'\left( x \right) = 0\) có hai nghiệm phân biệt
-
C.
Đồ thị (III) xảy ra khi \(a > 0\) và \(f'\left( x \right) = 0\) vô nghiệm hoặc có nghiệm kép.
-
D.
Đồ thị (IV) xảy ra khi \(a > 0\) và \(f'\left( x \right) = 0\) có có nghiệm kép.
Đáp án : C
Nhận xét các trường hợp xảy ra của từng đồ thị rồi xét tính đúng sai của từng đáp án.
Đáp án A sai vì đồ thị (I) xảy ra thì \(a > 0\)
Đáp án B sai vì đồ thị (II) xảy ra thì \(a < 0\)
Đáp án C đúng.
Đáp án D sai vì đồ thị (IV) xảy ra thì \(a < 0\)
Cho hàm số \(y = \dfrac{{2x + b}}{{cx + d}}\) có bảng biến thiên:
Giá trị của \(2{c^2} - 5{d^2}\) bằng
-
A.
$-3$
-
B.
$0$
-
C.
$2$
-
D.
$4$
Đáp án : A
- Quan sát bảng biến thiên, tìm các đường tiệm cận đứng, ngang của đồ thị hàm số.
- Tìm \(c,d \Rightarrow 2{c^2} - 5{d^2}\).
Đồ thị hàm số \(y = \dfrac{{2x + b}}{{cx + d}}\) có\( \Rightarrow \left\{ \begin{array}{l}c = 1\\d = 1\end{array} \right.\) \( \Rightarrow 2{c^2} - 5{d^2} = {2.1^2} - {5.1^2} = - 3\)
Cho hàm số \(y = {x^3} + 2m{x^2} + \left( {m + 3} \right)x + 4\,\,\,\left( {{C_m}} \right)\). Giá trị của tham số \(m\) để đường thẳng \(\left( d \right):y = x + 4\) cắt \(\left( {{C_m}} \right)\) tại ba điểm phân biệt \(A\left( {0;4} \right),\,\,B,\,\,C\) sao cho tam giác \(KBC\) có diện tích bằng \(8\sqrt 2 \) với điểm \(K\left( {1;3} \right)\) là:
-
A.
\(m = \frac{{1 - \sqrt {137} }}{2}\)
-
B.
\(m = \frac{{1 + \sqrt {137} }}{2}\)
-
C.
\(m = \frac{{1 \pm \sqrt {137} }}{2}\)
-
D.
\(m = \frac{{ \pm 1 + \sqrt {137} }}{2}\)
Đáp án : C
+ Xét phương trình hoành độ giao điểm và tìm mối quan hệ giữa \({x_1},{x_2}\) là hoành độ của \(B,C\).
+ Viết công thức tính diện tích tam giác \(KBC\) và tìm \(m\).
+ Xét phương trình hoành độ giao điểm của đồ thị và đường thẳng ta có:
\(\begin{array}{l}{x^3} + 2m{x^2} + \left( {m + 3} \right)x + 4 = x + 4\\ \Leftrightarrow {x^3} + 2m{x^2} + \left( {m + 2} \right)x = 0\\ \Leftrightarrow x\left( {{x^2} + 2mx + m + 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 0\\{x^2} + 2mx + m + 2 = 0\,\,\,\,\,\left( 1 \right)\end{array} \right.\end{array}\)
Để \(\left( d \right)\) cắt \(\left( {{C_m}} \right)\) tại 3 điểm phân biệt thì phương trình \(\left( 1 \right)\) có 2 nghiệm phân biệt khác 0
\( \Rightarrow \left\{ \begin{array}{l}\Delta ; > 0\\0 + 2m.0 + m + 2 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{m^2} - m - 2 > 0\\m \ne - 2\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m > 2\\m < - 1\end{array} \right.\\m \ne 2\end{array} \right.\) .
Gọi \({x_1};\,\,{x_2}\) là \(2\) nghiệm phân biệt của phương trình \(\left( 1 \right)\) \( \Rightarrow B\left( {{x_1};{x_1} + 4} \right);\,\,\,C\left( {{x_2};{x_2} + 4} \right).\)
Khi đó áp dụng định lí Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = - 2m\\{x_1}.{x_2} = m + 2\end{array} \right..\)
Ta có: \({S_{KBC}} = \frac{1}{2}.d\left( {K,BC} \right).BC.\)
Phương trình đường thẳng \(\left( d \right):\,\,y = x + 4 \Leftrightarrow x - y + 4 = 0\).
Vì \(B,\,\,C\) thuộc đường thẳng \(\left( d \right)\) nên ta có: \(d\left( {K,BC} \right) = d\left( {K;d} \right) = \frac{{\left| {1 - 3 + 4} \right|}}{{\sqrt {{1^2} + {{\left( { - 1} \right)}^2}} }} = \sqrt 2 .\)
\(\begin{array}{l}BC = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{x_2} + 4 - {x_1} - 4} \right)}^2}} \\BC = \sqrt {2{{\left( {{x_1} - {x_2}} \right)}^2}} \\BC = \sqrt 2 .\sqrt {{{\left( {{x_1} + {x_2}} \right)}^2} - 4{x_1}{x_2}} \\BC = \sqrt 2 .\sqrt {4{m^2} - 4\left( {m + 2} \right)} \\BC = 2\sqrt 2 .\sqrt {{m^2} - m - 2} \end{array}\)
Theo bài ra ta có:
\(\begin{array}{l}{S_{KBC}} = 8\sqrt 2 \\ \Leftrightarrow \frac{1}{2}.\sqrt 2 .2\sqrt 2 \sqrt {{m^2} - m - 2} = 8\sqrt 2 \\ \Leftrightarrow \sqrt {{m^2} - m - 2} = 4\sqrt 2 \\ \Leftrightarrow {m^2} - m - 2 = 32\\ \Leftrightarrow {m^2} - m - 34 = 0\\ \Leftrightarrow m = \frac{{1 \pm \sqrt {137} }}{2}\,\,\,\left( {tm} \right)\end{array}\)
Vậy \(m = \frac{{1 \pm \sqrt {137} }}{2}\).
Tiếp tuyến của đồ thị hàm số $y = \dfrac{{{x^3}}}{3} - 2{x^2} + x + 2$ song song với đường thẳng $y = - 2x + 5$ có phương trình là:
-
A.
$2x + y - \dfrac{{10}}{3} = 0$ và $2x + y - 2 = 0$
-
B.
$2x + y + \dfrac{4}{3} = 0$ và $2x + y + 2 = 0$
-
C.
$2x + y - 4 = 0$ và $2x + y - 1 = 0$
-
D.
$y = 2x + y - 3 = 0$ và $2x + y + 1 = 0$
Đáp án : A
Tiếp tuyến song song với đường thẳng $y = - 2x + 5$ thì có hệ số góc bằng với hệ số góc của đường thẳng nên $y' = - 2$.
Giải phương trình $y' = - 2$ tìm các nghiệm rồi suy ra tọa độ tiếp điểm, từ đó viết được phương trình tiếp tuyến.
Đường thẳng $d$ đi qua $A\left( {{x_0};{y_0}} \right)$ và có hệ số góc $k$ có phương trình $y = k\left( {x - {x_0}} \right) + {y_0}$
Tiếp tuyến $(d)$ song song với đường thẳng $y = - 2x + 5$ nên có hệ số góc .
Suy ra $y' = - 2$ hay ${x^2} - 4x + 1 = - 2 \Leftrightarrow \left( {x - 1} \right)\left( {x - 3} \right) = 0$ $ \Rightarrow \left[ \begin{gathered}x = 1,y = \dfrac{4}{3} \hfill \\x = 3,y = - 4 \hfill \\ \end{gathered} \right.$
Với $x = 1;y = \dfrac{4}{3}$ thì ${d_1}:y = - 2\left( {x - 1} \right) + \dfrac{4}{3}$ hay ${d_1}:y = - 2x + \dfrac{{10}}{3}$
Với $x = 3;y = - 4$ thì ${d_2}:y = - 2\left( {x - 3} \right) - 4$ hay ${d_2}:y = - 2x + 2$
Cho hàm số \(f\left( x \right) = a{x^4} + b{x^3} + c{x^2} + dx + e,\) với \(a,b,c,d,e \in \mathbb{R}.\) Hàm số \(y = f'\left( x \right)\) có đồ thị như hình vẽ. Trong các khẳng định sau, khẳng định nào đúng?
-
A.
\(a + b + c + d < 0\)
-
B.
\(a + c < b + d\)
-
C.
\(a + c > 0\)
-
D.
\(d + b - c > 0\)
Đáp án : C
Từ đồ thị hàm số suy ra \(f'\left( 0 \right) = 0;\,f'\left( x \right) > 0,\forall x \in \left( {0;1} \right)\)
Lập bảng biến thiên của hàm số $y=f(x)$
Ta có \(f'\left( x \right) = 4a{x^3} + 3b{x^2} + 2cx + d\)
Từ đồ thị hàm số ta thấy \(f'\left( 0 \right) \Leftrightarrow d = 0\)
Từ đồ thị ta thấy:
+ Khi $x< -1$ thì $f'(x)>0$.
+ Khi $-1<x<0=>f'(x)<0$
+ Khi $0<x<x_0$ (với $x_0$ là nghiệm thứ 3 của phương trình $f'(x)=0$) $=>f'(x)>0$
+ Khi $x>x_0$ thì $f'(x)<0$
Ta có bảng biến thiên:
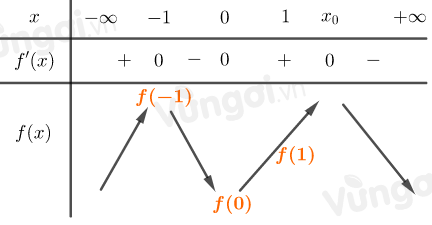
\(\Rightarrow f\left( { - 1} \right) > f\left( 0 \right)\)
\( \Leftrightarrow a - b + c - d + e > e \Leftrightarrow a + c > b + d\) nên B sai, lại có \(d = 0 \Rightarrow a + c > b\) (1)
+) Từ bảng biến thiên \( \Rightarrow f\left( 1 \right) > f\left( 0 \right)\)
\( \Leftrightarrow a + b + c + d + e > e \Leftrightarrow a + b + c + d > 0\) nên A sai.
Mà \(d = 0\) nên \(a + b + c > 0 \Leftrightarrow a + c > - b\) (2)
Từ (1) và (2) suy ra \(2\left( {a + c} \right) > 0 \Leftrightarrow a + c > 0.\)
Cho hai số thực \(x,\,y\) thỏa mãn \({x^2} + {y^2} - 4x + 6y + 4 + \sqrt {{y^2} + 6y + 10} = \sqrt {6 + 4x - {x^2}} \). Gọi \(M,\,m\) lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức \(T = \left| {\sqrt {{x^2} + {y^2}} - a} \right|\). Có bao nhiêu giá trị nguyên thuộc đoạn \(\left[ { - 10;\,10} \right]\) của tham số \(a\) để \(M \ge 2m\)?
-
A.
\(17\).
-
B.
\(16\).
-
C.
\(15\).
-
D.
\(18\).
Đáp án : B
Biến đổi đẳng thức đã cho để đưa về dạng phương trình đường tròn \(\left( C \right)\) tâm \(I\) bán kính \(R\).
Từ đó ta đưa bài toán về dạng bài tìm \(M\left( {x;y} \right) \in \left( C \right)\) để \(\left| {OM - a} \right|\) lớn nhất hoặc nhỏ nhất.
Xét các trường hợp xảy ra để tìm \(a.\)
Ta có \({x^2} + {y^2} - 4x + 6y + 4 + \sqrt {{y^2} + 6y + 10} = \sqrt {6 + 4x - {x^2}} \)
\(\begin{array}{l} \Leftrightarrow {x^2} + {y^2} - 4x + 6y + 4 + \sqrt {{y^2} + 6y + 10} - \sqrt {6 + 4x - {x^2}} = 0\\ \Leftrightarrow {x^2} + {y^2} - 4x + 6y + 4 + \dfrac{{\left( {\sqrt {{y^2} + 6y + 10} - \sqrt {6 + 4x - {x^2}} } \right)\left( {\sqrt {{y^2} + 6y + 10} + \sqrt {6 + 4x - {x^2}} } \right)}}{{\sqrt {{y^2} + 6y + 10} + \sqrt {6 + 4x - {x^2}} }} = 0\end{array}\)
\(\begin{array}{l} \Leftrightarrow {x^2} + {y^2} - 4x + 6y + 4 + \dfrac{{{y^2} + 6y + 10 - 6 - 4x + {x^2}}}{{\sqrt {{y^2} + 6y + 10} + \sqrt {6 + 4x - {x^2}} }} = 0\\ \Leftrightarrow {x^2} + {y^2} - 4x + 6y + 4 + \dfrac{{{x^2} + {y^2} - 4x + 6y + 4}}{{\sqrt {{y^2} + 6y + 10} + \sqrt {6 + 4x - {x^2}} }} = 0\end{array}\)
\( \Leftrightarrow \left( {{x^2} + {y^2} - 4x + 6y + 4} \right)\left( {1 + \dfrac{1}{{\sqrt {{y^2} + 6y + 10} + \sqrt {6 + 4x - {x^2}} }}} \right) = 0\)
\( \Leftrightarrow {x^2} + {y^2} - 4x + 6y + 4 = 0\) (vì \(1 + \dfrac{1}{{\sqrt {{y^2} + 6y + 10} + \sqrt {6 + 4x - {x^2}} }} > 0\) )
\( \Leftrightarrow {\left( {x - 2} \right)^2} + {\left( {y + 3} \right)^2} = 9\)
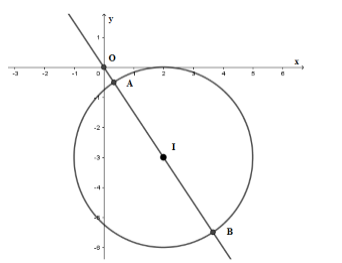
Phương trình \({\left( {x - 2} \right)^2} + {\left( {y + 3} \right)^2} = 9\) là phương trình đường tròn \(\left( C \right)\) tâm \(I\left( {2; - 3} \right)\) và bán kính \(R = 3.\)
Gọi \(N\left( {x;y} \right) \in \left( C \right)\) ta suy ra \(ON = \sqrt {{x^2} + {y^2}} \) suy ra \(T = \left| {ON - a} \right|\)
Gọi \(A,B\) là giao điểm của đường tròn \(\left( C \right)\) và đường thẳng \(OI\).
Khi đó \(OA = OI - R = \sqrt {13} - 3\) và \(OB = OI + R = \sqrt {13} + 3\)
Suy ra \(\sqrt {13} - 3 \le \sqrt {{x^2} + {y^2}} \le \sqrt {13} + 3\)
TH1: Nếu \(\sqrt {13} - 3 \le a \le \sqrt {13} + 3\) thì \(\left| {\sqrt {{x^2} + {y^2}} - a} \right| \ge 0 \Rightarrow \min T = 0 \Rightarrow M \ge 2m \Rightarrow a \in \left\{ {1;2;3;4;5;6} \right\}\)
TH2: Nếu \(a < \sqrt {13} - 3 \Rightarrow a < \sqrt {13} \) nên \(\left| {\sqrt {13} + 3 - a} \right| > \left| {\sqrt {13} - 3 - a} \right|\), do đó \(M = \left| {\sqrt {13} + 3 - a} \right|;m = \left| {\sqrt {13} - 3 - a} \right|\)
Vì \(M \ge 2m \Rightarrow \left| {\sqrt {13} + 3 - a} \right| \ge 2\left| {\sqrt {13} - 3 - a} \right|\)
\( \Leftrightarrow {\left( {\sqrt {13} + 3 - a} \right)^2} - {\left( {2\sqrt {13} - 6 - 2a} \right)^2} \ge 0 \Leftrightarrow \sqrt {13} - 9 \le a \le \sqrt {13} - 1 \Rightarrow a \in \left\{ { - 5; - 4; - 3; - 2; - 1;0} \right\}\)
TH3: Nếu \(a > \sqrt {13} + 3 \Rightarrow a > \sqrt {13} \) nên \(\left| {\sqrt {13} + 3 - a} \right| < \left| {\sqrt {13} - 3 - a} \right|\), do đó \(m = \left| {\sqrt {13} + 3 - a} \right|;M = \left| {\sqrt {13} - 3 - a} \right|\)
Vì \(M \ge 2m \Rightarrow \left| {\sqrt {13} - 3 - a} \right| \ge 2\left| {\sqrt {13} + 3 - a} \right|\)
\( \Leftrightarrow {\left( {\sqrt {13} - 3 - a} \right)^2} - {\left( {2\sqrt {13} + 6 - 2a} \right)^2} \ge 0 \Leftrightarrow \sqrt {13} + 1 \le a \le \sqrt {13} + 9 \Rightarrow a \in \left\{ {7;8;9;10} \right\}\)
Vậy có 16 giá trị của \(a\) thỏa mãn đề bài.
Cho hàm số \(y = f\left( x \right) = {2^{2019}}{x^3} + {3.2^{2018}}{x^2} - 2018\) có đồ thị cắt trục hoành tại ba điểm phân biệt có hoành độ \({x_1};{x_2};{x_3}\). Tính giá trị biểu thức \(P = \dfrac{1}{{f'\left( {{x_1}} \right)}} + \dfrac{1}{{f'\left( {{x_2}} \right)}} + \dfrac{1}{{f'\left( {{x_3}} \right)}}.\)
-
A.
\(P = {3.2^{2018}}\)
-
B.
\(P = - 2018\)
-
C.
\(P = 0\)
-
D.
\(P = {2^{2019}}\)
Đáp án : C
Sử dụng hệ thức Vi-et cho phương trình bậc ba \(a{x^3} + b{x^2} + cx + d = 0\,\left( {a \ne 0} \right)\) có ba nghiệm \({x_1},{x_2},{x_3}\)
\(\left\{ \begin{array}{l}{x_1} + {x_2} + {x_3} = \dfrac{{ - b}}{a}\\{x_1}{x_2} + {x_2}{x_3} + {x_1}{x_3} = \dfrac{c}{a}\\{x_1}{x_2}{x_3} = - \dfrac{d}{a}\end{array} \right.\)
Sau đó biến đổi \(f'\left( x \right)\) để tính \(P.\)
Ta có \(f\left( x \right) = {2^{2019}}{x^3} + {3.2^{2018}}{x^2} - 2018\)
\( \Rightarrow f'\left( x \right) = {3.2^{2019}}{x^2} + {3.2^{2019}}x = {3.2^{2019}}x\left( {x + 1} \right)\) \( \Rightarrow \dfrac{1}{{f'\left( x \right)}} = \dfrac{1}{{{{3.2}^{2019}}}}.\dfrac{1}{{x.\left( {x + 1} \right)}} = \dfrac{1}{{{{3.2}^{2019}}}}\left( {\dfrac{1}{x} - \dfrac{1}{{x + 1}}} \right)\)
Xét phương trình hoành độ giao điểm của đồ thị hàm số với trục hoành \({2^{2019}}{x^3} + {3.2^{2018}}{x^2} - 2018 = 0\) (*)
Vì \({x_1},{x_2},{x_3}\) là ba ngiệm của phương trình (*) nên theo hẹ thức Vi-et ta có
\(\left\{ \begin{array}{l}{x_1} + {x_2} + {x_3} = \dfrac{{ - 3}}{2}\\{x_1}{x_2} + {x_2}{x_3} + {x_1}{x_3} = 0\\{x_1}{x_2}{x_3} = \dfrac{{2018}}{{{2^{2019}}}}\end{array} \right.\)
Ta có \(P = \dfrac{1}{{f'\left( {{x_1}} \right)}} + \dfrac{1}{{f'\left( {{x_2}} \right)}} + \dfrac{1}{{f'\left( {{x_3}} \right)}} = \dfrac{1}{{{{3.2}^{2019}}}}\left( {\dfrac{1}{{{x_1}}} - \dfrac{1}{{{x_1} + 1}} + \dfrac{1}{{{x_2}}} - \dfrac{1}{{{x_2} + 1}} + \dfrac{1}{{{x_3}}} - \dfrac{1}{{{x_3} + 1}}} \right)\)
\( = \dfrac{1}{{{{3.2}^{2019}}}}\left[ {\left( {\dfrac{1}{{{x_1}}} + \dfrac{1}{{{x_2}}} + \dfrac{1}{{{x_3}}}} \right) - \left( {\dfrac{1}{{{x_1} + 1}} + \dfrac{1}{{{x_2} + 1}} + \dfrac{1}{{{x_3} + 1}}} \right)} \right]\)
\( = \dfrac{1}{{{{3.2}^{2019}}}}\left[ {\dfrac{{{x_1}{x_2} + {x_2}{x_3} + {x_1}{x_3}}}{{{x_1}{x_2}{x_3}}} - \dfrac{{\left( {{x_2} + 1} \right)\left( {{x_3} + 1} \right) + \left( {{x_1} + 1} \right)\left( {{x_3} + 1} \right) + \left( {{x_1} + 1} \right)\left( {{x_2} + 1} \right)}}{{\left( {{x_1} + 1} \right)\left( {{x_2} + 1} \right)\left( {{x_3} + 1} \right)}}} \right]\)
\( = \dfrac{1}{{{{3.2}^{2019}}}}\left( {0 - \dfrac{{{x_1}{x_2} + {x_2}{x_3} + {x_1}{x_3} + 2\left( {{x_1} + {x_2} + {x_3}} \right) + 3}}{{\left( {{x_1} + 1} \right)\left( {{x_2} + 1} \right)\left( {{x_3} + 1} \right)}}} \right)\)
\( = \dfrac{1}{{{{3.2}^{2019}}}}.\dfrac{{0 + 2.\dfrac{{ - 3}}{2} + 3}}{{\left( {{x_1} + 1} \right)\left( {{x_2} + 1} \right)\left( {{x_3} + 1} \right)}} = 0\)
>> Luyện thi TN THPT & ĐH năm 2024 trên trang trực tuyến Tuyensinh247.com. Học mọi lúc, mọi nơi với Thầy Cô giáo giỏi, đầy đủ các khoá: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng; Tổng ôn chọn lọc.
 |
 |
 |
 |
 |
 |
 |
 |
