Câu hỏi 3 trang 86 SGK Hình học 10
Trong phương trình (1) hãy giải thích vì sao...
Đề bài
Trong phương trình (1) hãy giải thích vì sao ta luôn đặt được \(b^2=a^2-c^2\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
- Tìm tọa độ \(B_2\).
- Sử dụng định lý Pi-ta-go trong tam giác kết hợp điều kiện điểm thuộc elip để suy ra điều phải chứng minh.
Lời giải chi tiết
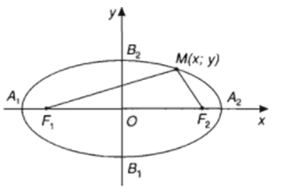
Do \(F_1(-c;0),F_2(c;0)\) nên \(OF_1=OF_2=c\)
\(B_1(0;-b),B_2(0;b)\)
\( \Rightarrow {B_2}{F_1} = {B_2}{F_2} = \sqrt {{b^2} + {c^2}} \)
Do \(B_2\) thuộc elip nên:
\(\eqalign{
& {B_2}{F_1} + {B_2}{F_2} = 2a \Rightarrow 2\sqrt {{b^2} + {c^2}} = 2a \cr
& \Rightarrow {b^2} + {c^2} = {a^2} \Leftrightarrow {b^2} = {a^2} - {c^2} \cr} \)
Cách khác:
Do \(F_1(-c;0),F_2(c;0)\) nên \({F_1}{F_2} = 2c\).
Xét tam giác \(MF_1F_2\) có:
\(M{F_1} + M{F_2} > {F_1}{F_2}\) \( \Rightarrow 2a > 2c \) \(\Leftrightarrow a > c \) \(\Rightarrow {a^2} - {c^2} > 0\)
Do đó có thể đặt \({b^2} = {a^2} - {c^2}\).
Loigiaihay.com
Bình luận
Chia sẻ
- Câu hỏi 4 trang 87 SGK Hình học 10
- Bài 1 trang 88 SGK Hình học 10
- Bài 2 trang 88 SGK Hình học 10
- Bài 3 trang 88 SGK Hình học 10
- Bài 4 trang 88 SGK Hình học 10
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
