Cách tìm thiết diện của hình khối cắt bởi mặt phẳng - Toán 11

Cho hình (H) và mặt phẳng (P) cắt hình (H).

Thiết diện là phần chung của mặt phẳng (P) và hình (H).

Bước 1: Tìm giao tuyến đầu tiên của mặt phẳng (P) với một mặt phẳng \(\left( \alpha  \right)\) của hình (H), sau đó kéo dài giao tuyến này cắt các cạnh khác của hình (H), từ đó tìm được các giao tuyến tiếp theo.

Bước 2: Kết luận: Đa giác giới hạn bởi các đoạn giao tuyến này khép kín thành một thiết diện cần tìm.

1) Cho hình chóp S.ABCD. Gọi M là một điểm trong tam giác SCD.

a) Tìm giao tuyến của hai mặt phẳng (SBM) và (SAC).

b) Tìm giao điểm của đường thẳng BM và (SAC).

c) Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng (ABM).

Giải:

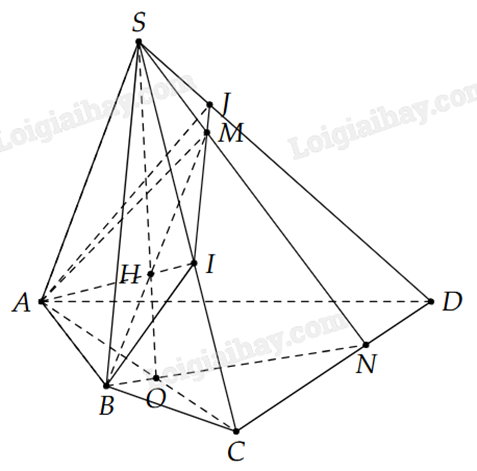
a) Tìm \((SBM) \cap (SAC)\).

Trong mặt phẳng (SCD), gọi \(N = SM \cap CD\).

Trong mặt phẳng (ABCD), gọi \(O = AC \cap BN\).

Ta có: \(\left\{ {\begin{array}{*{20}{l}}{O \in BN \subset (SBN)}\\{O \in AC \subset (SAC)}\end{array}} \right. \Rightarrow O \in (SAC) \cap (SBN)\) (1)

Mặt khác \(S \in (SAC) \cap (SBN)\) (2)

Từ (1) và (2) suy ra \((SAC) \cap (SBN) = SO\).

Vì \((SBM) \equiv (SBN)\) nên \((SBM) \cap (SAC) = SO\).

b) Tìm \(BM \cap (SAC)\).

Gọi \(H = BM \cap SO\).

Ta có \(\left\{ {\begin{array}{*{20}{l}}{H \in BM}\\{H \in SO \subset (SAC)}\end{array}} \right. \Rightarrow H = BM \cap (SAC)\).

c) Xác định thiết diện của hình chóp với (ABM).

Trong \((SAC)\), gọi \(I = AH \cap SC\). Ta có:

\(\left\{ {\begin{array}{*{20}{l}}{I \in AH \subset (ABM)}\\{I \in SC \subset (SCD)}\end{array}} \right. \Rightarrow I \in (SCD) \cap (ABM)\) (3)

Mặt khác \(M \in (SCD) \cap (ABM)\) (4)

Từ (3) và (4) suy ra \((SCD) \cap (ABM) = IM\).

Trong \((SCD)\), gọi \(J = IM \cap SD\). Khi đó:

\((SAD) \cap (ABM) = AJ\), \((SBC) \cap (ABM) = BI\).

Vậy thiết diện cần tìm là ngũ giác ABIJM.

2) Cho tứ diện ABCD. Trên AB, AC lấy 2 điểm M, N sao cho MN không song song BC. Gọi O là một điểm trong tam giác BCD.

a) Tìm giao tuyến của (OMN) và (BCD).

b) Tìm giao điểm của DC, BD với (OMN).

c) Tìm thiết diện của (OMN) với tứ diện.

Giải:

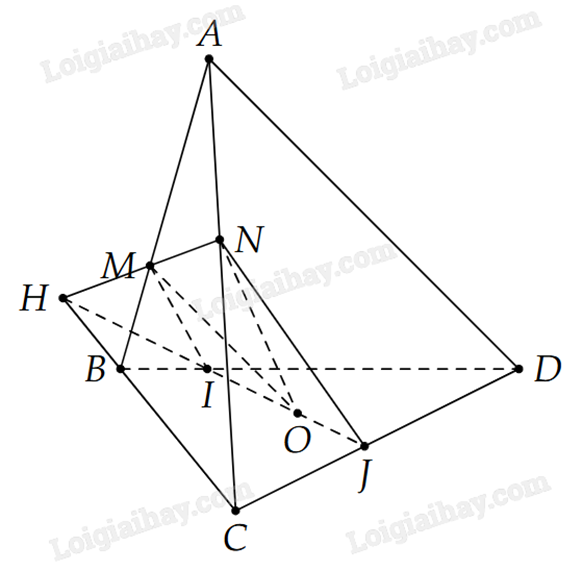
a) Tìm giao tuyến của (OMN) và (BCD).

Trong (ABC), gọi \(H = MN \cap BC\).

Ta có \(\left\{ {\begin{array}{*{20}{l}}{H \in MN \subset (OMN)}\\{H \in BC \subset (BCD)}\end{array}} \right. \Rightarrow H \in (OMN) \cap (BCD)\) (1)

Mặt khác \(O \in (OMN) \cap (BCD)\) (2)

Từ (1) và (2) suy ra OH là giao tuyến cần tìm.

b) Tìm giao điểm của DC, BD với (OMN).

Trong (BCD), gọi \(I = BD \cap HO\).

Ta có \(\left\{ {\begin{array}{*{20}{l}}{I \in BD}\\{I \in HO \subset (MNO)}\end{array}} \right. \Rightarrow I = BD \cap (MNO)\).

Trong \((BCD)\), gọi \(J = CD \cap HO\).

Ta có \(\left\{ {\begin{array}{*{20}{l}}{J \in CD}\\{J \in HO \subset (MNO)}\end{array}} \right. \Rightarrow J = CD \cap (MNO)\).

c) Tìm thiết diện của (OMN) và hình chóp.

Ta có \(\left\{ {\begin{array}{*{20}{l}}{(ABC) \cap (MNO) = MN}\\{(ABD) \cap (MNO) = MI}\\{(ACD) \cap (MNO) = NJ}\\{(BCD) \cap (MNO) = II}\end{array}} \right.\).

Vậy thiết diện cần tìm là tứ giác MNJI.