Cách chứng minh ba điểm thẳng hàng trong hình học không gian - Toán 11

Muốn chứng minh ba điểm A, B, C thẳng hàng, ta chứng minh ba điểm đó lần lượt thuộc hai mặt phẳng phân biệt \(\left( \alpha  \right)\) và \(\left( \beta  \right)\) thì suy ra ba điểm A, B, C nằm trên giao tuyến của \(\left( \alpha  \right)\) và \(\left( \beta  \right)\), nên chúng thẳng hàng.

1) Cho tứ diện SABC. Trên SA, SB và SC lần lượt lấy các điểm D, E, F sao cho DE cắt AB tại I, EF cắt BC tại J, FD cắt CA tại K. Chứng minh ba điểm I, J, K thẳng hàng.

Giải:

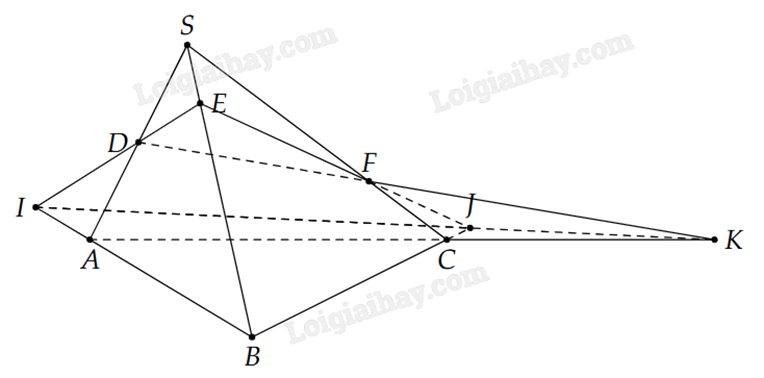
Ta có:

\(\left\{ {\begin{array}{*{20}{l}}{I = AB \cap DE(AB,DE \subset (SAB))}\\{I \in AB,AB \subset (ABC)}\\{I \in DE,DE \subset (DEF)}\end{array}} \right. \Rightarrow I \in (ABC) \cap (DEF)\) (1)

\(\left\{ {\begin{array}{*{20}{l}}{K = AC \cap DF(AC,DF \subset (SAC))}\\{K \in AC,AC \subset (ABC)}\\{K \in DF,DF \subset (DEF)}\end{array} \Rightarrow K \in (ABC) \cap (DEF)} \right.\) (2)

\(\left\{ {\begin{array}{*{20}{l}}{J = BC \cap EF(BC,EF \subset (SBC))}\\{J \in BC,BC \subset (ABC)}\\{J \in EF,EF \subset (DEF)}\end{array}} \right. \Rightarrow J \in (ABC) \cap (DEF)\) (3)

Từ (1), (2), (3) suy ra ba điểm I, J, K thẳng hàng.

2) Cho tứ diện ABCD có G là trọng tâm tam giác BCD. Gọi M, N, P lần lượt là trung điểm của AB, BC, CD.

a) Tìm giao tuyển của (AND) và (ABP).

b) Gọi \(I = AG \cap MP\), \(J = CM \cap AN\). Chứng minh D, I, J thẳng hàng.

Giải:

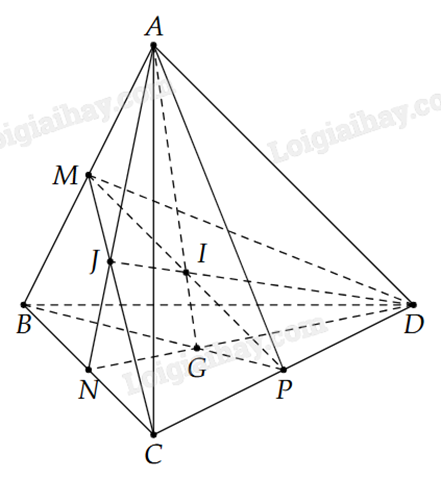
a) \(A \in (ABP) \cap (ADN)\) (1)

Ta có \(G = BP \cap DN\), có \(\left\{ {\begin{array}{*{20}{l}}{G \in BP,}&{BP \subset (ABP)}\\{G \in DN,}&{DN \subset (ADN)}\end{array}} \right. \Rightarrow G \in (ABP) \cap (ADN)\) (2)

Từ (1) và (2) ta có \(AG = (ABP) \cap (ADN)\).

b) \(I = AG \cap MP\), \(AG \subset (ADG)\), \(MP \subset (DMN) \Rightarrow I \in (ADG) \cap (DMN)\) (3)

\(J = CM \cap AN\), \(AN \subset (ADG)\), \(CM \subset (DMN) \Rightarrow J \in (ADG) \cap (DMN)\) (4)

\(D \in (ADG) \cap (DMN)\) (5)

Từ (3), (4), (5) suy ra ba điểm D, I, J thuộc giao tuyến của hai mặt phẳng (ADG) và (DMN).

Vậy ba điểm D, I, J thẳng hàng.

3) Cho hình bình hành ABCD. S là điểm không thuộc (ABCD), M và N lần lượt là trung điểm của đoạn thẳng AB và SC.

a) Xác định giao điểm \(I = AN \cap (SBD)\).

b) Xác định giao điểm \(J = MN \cap (SBD)\).

c) Chứng minh ba điểm I, J, B thẳng hàng.

Giải:

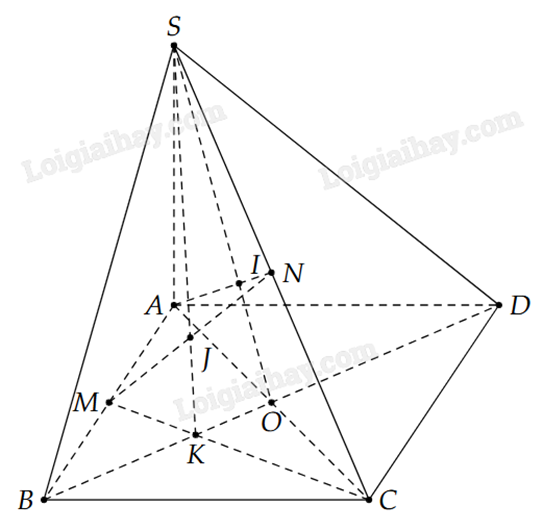
a) Chọn mặt phẳng phụ (SAC) chứa AN. Ta tìm giao tuyến của (SAC) và (SBD).

Trong mặt phẳng (ABCD) gọi O là giao điểm của AC và BD. Hai mặt phẳng (SAC) và (SBD) có hai điểm chung là S và O.

Vậy \((SAC) \cap (SBD) = SO\).

Trong mặt phẳng (SAC) gọi \(I = AN \cap SO\). Ta có \(I = AN \cap (SBD)\).

b) Chọn mặt phẳng phụ (SMC) chứa MN. Ta tìm giao tuyến của (SMC) và (SBD).

Trong mặt phẳng (ABCD) gọi K là giao điểm của MC và BD. Hai mặt phẳng (SMC) và (SBD) có hai điểm chung là S và K.

Vậy \((SMC) \cap (SBD) = SK\).

Trong mặt phẳng (SMC) gọi \(J = MN \cap SK\). Ta có \(J = MN \cap (SBD)\).

c) Ta có B là điểm chung của (ABN) và (SBD) (1)

\(\left\{ {\begin{array}{*{20}{l}}{I \in SO,SO \subset (SBD)}\\{I \in AN,AN \subset (ABN)}\end{array}} \right. \Rightarrow I \in (ABN) \cap (SBD)\) (2)

\(\left\{ {\begin{array}{*{20}{l}}{J \in SK,SK \subset (SBD)}\\{J \in MN,MN \subset (ABN)}\end{array}} \right. \Rightarrow J \in (ABN) \cap (SBD)\) (3)

Từ (1), (2) và (3) suy ra ba điểm I, J, B thẳng hàng.