Tính chất và cách chứng minh hai đường thẳng song song trong không gian - Toán 11

Định lí 1: Trong không gian, qua một điểm không nằm trên đường thẳng cho trước, có một và chỉ một đường thẳng song song với đường thẳng đã cho.

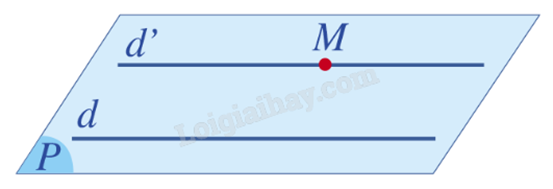
Định lí 2 (về giao tuyến của ba mặt phẳng): Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy đồng quy, hoặc đôi một song song với nhau.

Hệ quả Định lí 2: Nếu hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của chúng (nếu có) cũng song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.

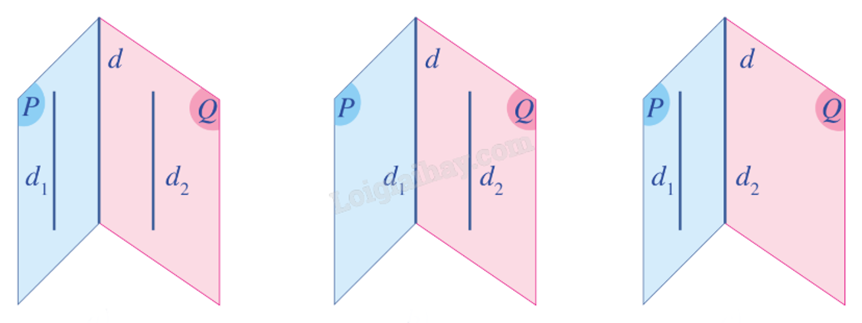
Định lí 3: Trong không gian, hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì song song với nhau.

Ta sử dụng các định lí trên để chứng minh hai đường thẳng song song trong không gian. Ngoài ra, có thể dựa vào hình học phẳng: Định lí Thalès, đường trung bình, tính song song của cặp cạnh đối các hình (bình hành, thoi, chữ nhật, vuông).

1) Cho hình chóp S.ABCD có đáy ABCD là hình thang với AB // CD. Xác định giao tuyến của hai mặt phẳng (SAB) và (SCD).

Giải:

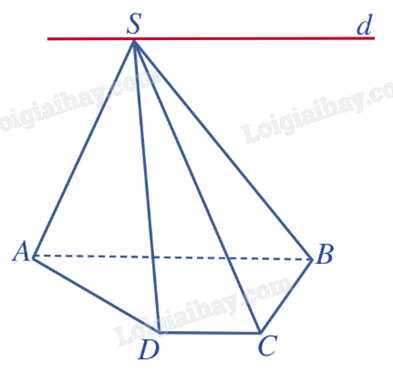
Hai mặt phẳng (SAB) và (SCD) có điểm chung là S và lần lượt chứa hai đường thẳng AB và CD song song với nhau nên giao tuyến của hai mặt phẳng đó là đường thẳng d đi qua S và song song với AB và CD.

2) Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của các cạnh SA, SD và P là một điểm nằm trên cạnh AB (P khác đường thẳng MN song song với đường thẳng PQ.

Giải:

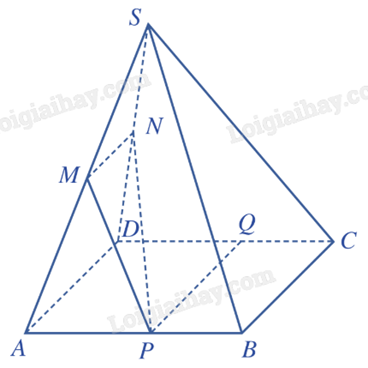
Ba mặt phẳng (SAD), (ABCD), (MNP) đôi một cắt nhau theo các giao tuyến AD, MN, PQ.

Trong tam giác SAD, ta có MN là đường trung bình nên MN // AD. Do đó theo Định lí 2, ta suy ra ba đường thẳng AD, MN, PQ đôi một song song. Vậy đường thẳng MN song song với đường thẳng PQ.

3) Cho tứ diện ABCD. Gọi M, N, P, Q, R và S lần lượt là trung điểm của các đoạn thẳng AB, CD, BC, AD, AC và BD. Chứng minh rằng:

a) MP // QN và MP = QN;

b) Các đoạn thẳng MN, PQ, RS cùng đi qua trung điểm G của mỗi đoạn.

Giải:

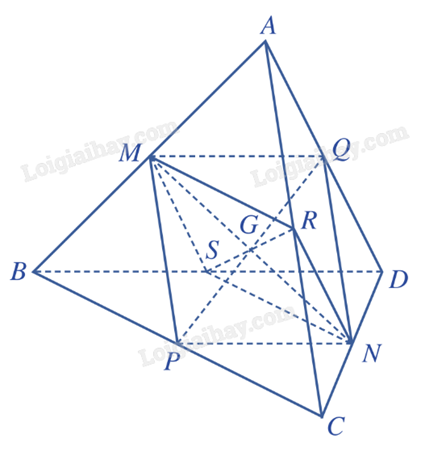
a) Trong tam giác ABC, ta có MP là đường trung bình nên MP // AC và \(MP = \frac{1}{2}AC\) (1).

Trong tam giác ACD, ta có QN là đường trung bình nên QN // AC và \(QN = \frac{1}{2}AC\) (2).

Từ (1) và (2) suy ra MP // QN và MP = QN.

b) Từ kết quả câu a, ta có tứ giác MPNQ là hình bình hành nên MN, PQ cắt nhau tại trung điểm G của mỗi đoạn.

Lập luận tương tự, ta cũng có tứ giác MSNR là hình bình hành nên MN, RS cắt nhau tại trung điểm G của mỗi đoạn. Vậy MN, PQ, RS cùng đi qua trung điểm G của mỗi đoạn.