Phép chiếu song song là gì? - Toán 11

Trong không gian, cho mặt phẳng (P) và đường thẳng \(l\) cắt (P). Với mỗi điểm M trong không gian, vẽ một đường thẳng đi qua M và song song hoặc trùng với \(l\). Đường thẳng này cắt (P) tại M’. Phép cho tương ứng mỗi điểm M trong không gian với điểm M’ trong (P) được gọi là phép chiếu song song lên mặt phẳng (P) theo phương \(l\).

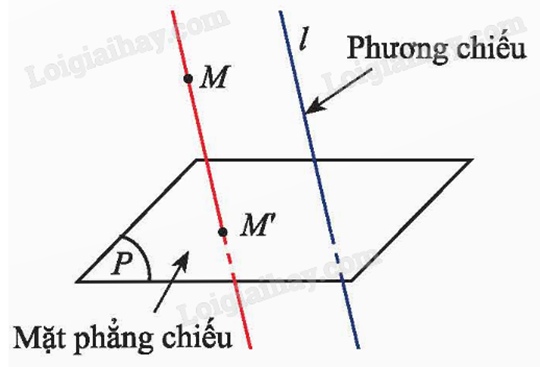
+ Mặt phẳng (P) được gọi là mặt phẳng chiếu và đường thẳng \(l\) được gọi là phương chiếu của phép chiếu song song nói trên.

+ Phép chiếu song song theo phương \(l\) còn được gọi tắt là phép chiếu theo phương \(l\).

+ Điểm M’ gọi là ảnh của điểm M qua phép chiếu theo phương \(l\).

+ Cho hình H trong không gian. Ta gọi tập hợp H’ các ảnh M’ của tất cả những điểm M thuộc H qua phép chiếu song song theo phương \(l\) là  hình chiếu song song của H lên mặt phẳng (P).

- Hình chiếu song song của một đường thẳng là một đường thẳng. Hình chiếu song song của một đoạn thẳng là một đoạn thẳng. Hình chiếu song song của một tia là một tia.

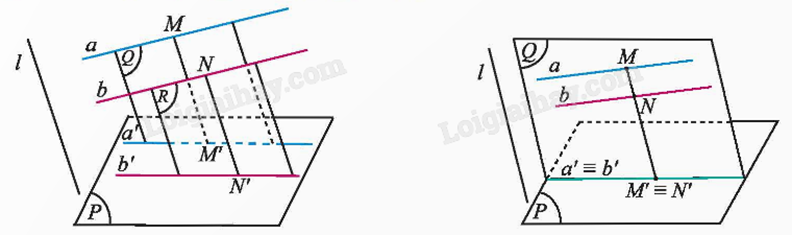
- Hình chiếu song song của hai đường thẳng song song là hai đường thẳng song song.

- Phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó.

- Phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng nằm trên hai đường thẳng song song hoặc trùng nhau.

1)

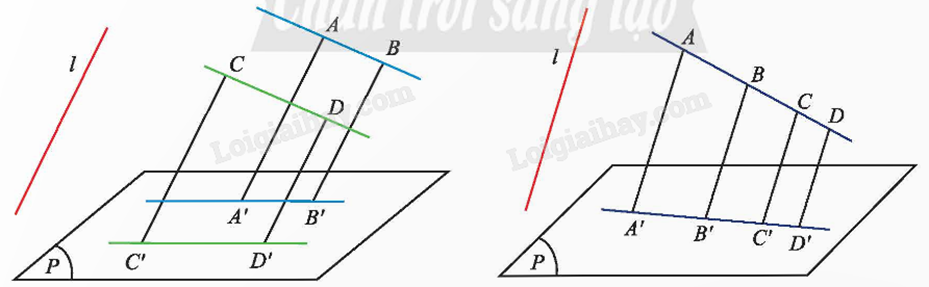
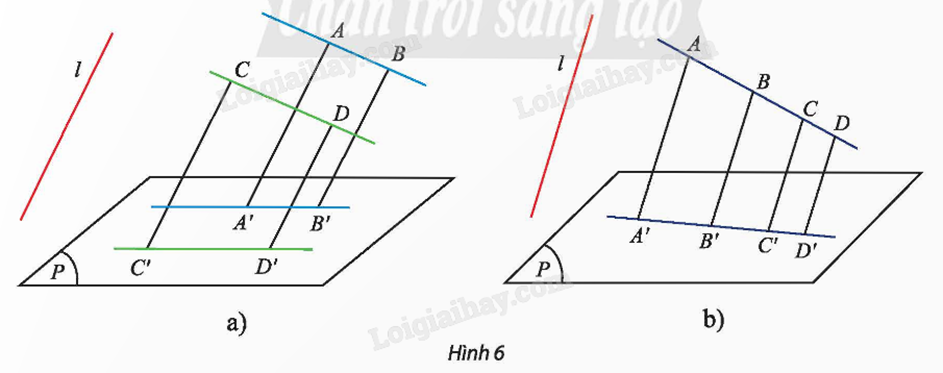
a) Tìm hình chiếu song song của đoạn thẳng AC, tia AB và đường thẳng AD trong Hình 6b.

b) Quan sát Hình 6a và so sánh hai tỉ số \(\frac{{AB}}{{CD}}\) và \(\frac{{A'B'}}{{C'D'}}\).

c) Quan sát Hình 6b và so sánh hai tỉ số \(\frac{{DA}}{{DB}}\) và \(\frac{{D'A'}}{{D'B'}}\).

Giải:

a) Trong Hình 6b, hình chiếu song song của đoạn thẳng AC, tia AB và đường thẳng AD lần lượt là đoạn thẳng A'C', tia A'B' và đường thẳng A'D'.

b) Do phép chiếu song song không làm thay đổi tỉ số độ dài của các đoạn thẳng nằm trên hai đường thẳng song song nên trong Hình 6a, ta có: \(\frac{{AB}}{{CD}} = \frac{{A'B'}}{{C'D'}}\).

c) Do phép chiếu song song không làm thay đổi tỉ số độ dài của các đoạn thẳng cùng thuộc một đường thẳng nên trong Hình 6b, ta có: \(\frac{{DA}}{{DB}} = \frac{{D'A'}}{{D'B'}}\).

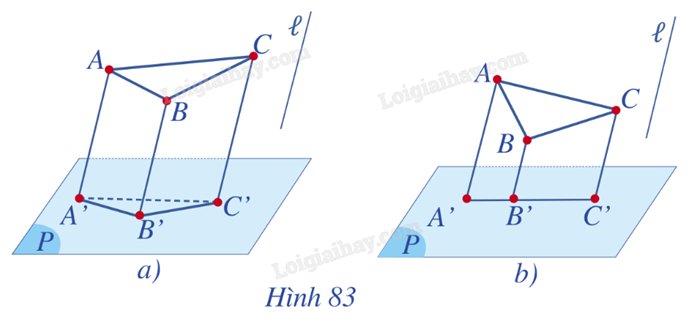
2) Cho mặt phẳng (P), tam giác ABC và đường thẳng \(l\) cắt mặt phẳng (P) sao cho các đường thẳng AB, BC, CA đều không song song hoặc trùng với đường thẳng \(l\). Xác định hình chiếu song song của tam giác ABC trên mặt phẳng (P) theo phương \(l\) trong mỗi trường hợp sau:

a) Mặt phẳng (ABC) không song song với \(l\);

b) Mặt phẳng (ABC) song song hoặc chứa \(l\).

Giải:

Gọi A', B', C' lần lượt là hình chiếu song song của ba điểm A, B, C trên mặt phẳng (P) theo phương \(l\).

a) Hình chiếu của tam giác ABC trên mặt phẳng (P) là tam giác A'B'C' (Hình 83a).

b) Ba điểm A', B', C' thuộc giao tuyến của hai mặt phẳng (ABC) và (P) nên ba điểm A', B', C' thẳng hàng và có một điểm nằm giữa hai điểm còn lại. Giả sử điểm B' nằm giữa hai điểm A' và C'. Khi đó, hình chiếu song song của tam giác ABC trên mặt phẳng (P) là đoạn thẳng A'C' (Hình 83b).