Cách chứng minh ba đường thẳng đồng quy trong hình học không gian - Toán 11

Ta tìm giao điểm của hai đường thẳng trong ba đường thẳng đã cho, rồi chứng minh giao điểm đó nằm trên đường thẳng thứ ba. Cụ thể:

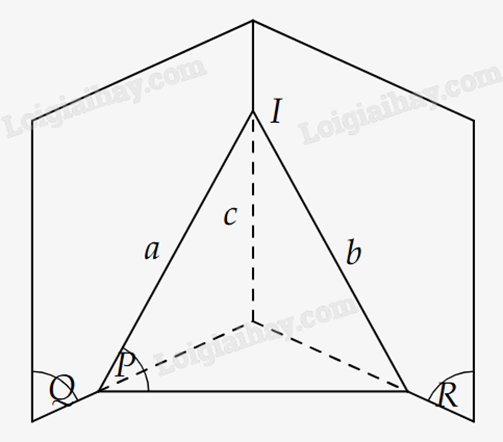
Bước 1: Chọn một mặt phẳng (P) chứa hai đường thẳng a, b. Gọi I là giao điểm của a và b.

Bước 2: Tìm một mặt phẳng (Q) chứa đường thẳng a, tìm một mặt phẳng (R) chứa đường thẳng b, sao cho c là giao tuyến của (P) và (Q), suy ra I thuộc (C).

Vậy, ba đường thẳng a, b, c đồng quy tại I.

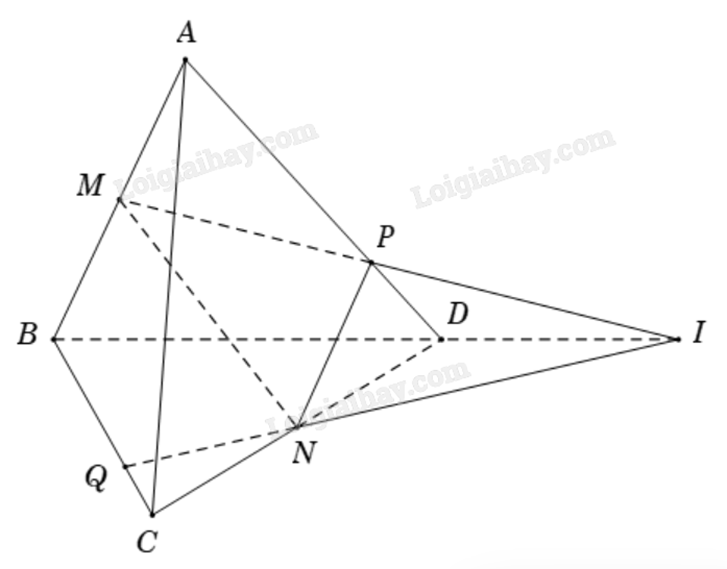
1) Cho tứ diện ABCD. Gọi M; N lần lượt là trung điểm của AB và CD. Mặt phẳng (P) qua MN và cắt AD; BC lần lượt tại P và Q. Biết MP cắt NQ tại I. Chứng minh rằng MP, NQ và BD đồng quy tại I.

Giải:

Giải:

Ta có \(\left( {ABD} \right) \cap \left( {BCD} \right) = BD\).

Lại có \(I \in MP \subset (ABD)\) và \(I \in NQ \subset (BCD)\) nên I là điểm chung của hai mặt phẳng (ABD) và (BCD). Nói cách khác, I thuộc vào giao tuyến của hai mặt phẳng (ABD) và (BCD).

Do đó, \(I \in BD\) hay ba đường thẳng MP, NQ và BD đồng quy tại I.

2) Cho hình chóp S.ABCD. Gọi M, N, P lần lượt là trung điểm của SA, SB, SC. Gọi \(E = AB \cap CD\), \(K = AD \cap BC\).

a) Tìm giao tuyến của hai mặt phẳng \((SAC) \cap (SBD)\), \((MNP) \cap (SBD)\).

b) Tìm giao điểm Q của đường thẳng SD với mặt phẳng (MNP).

c) Gọi \(H = NM \cap PQ\). Chứng minh ba điểm S, H, E thẳng hàng.

d) Chứng minh ba đường thẳng SK, QM, NP đồng quy.

Giải:

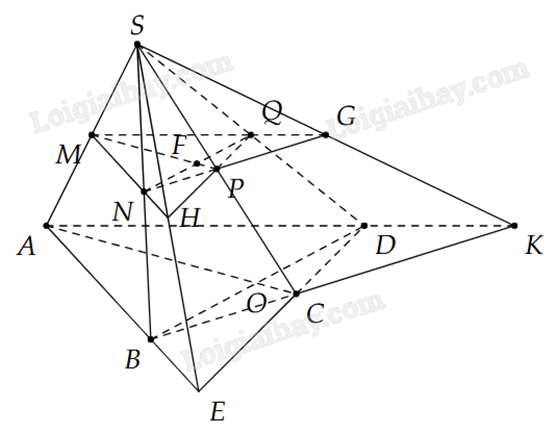
a) Trong mặt phẳng ABCD gọi \(O = AC \cap BD\), có:

\(\left\{ {\begin{array}{*{20}{l}}{O \in AC,AC \subset (SAC)}\\{O \in BD,BD \subset (SBD)}\end{array}} \right. \Rightarrow O \in (SAC) \cap (SBD)\) (1)

\(S \in (SAC) \cap (SBD)\) (2)

Từ (1) và (2) suy ra \((SAC) \cap (SBD) = SO\).

Trong mặt phẳng (SAC) gọi \(F = MP \cap SO\), có:

\(\left\{ {\begin{array}{*{20}{l}}{F \in MP,MP \subset (MNP)}\\{F \in SO,SO \subset (SBD)}\end{array}} \right. \Rightarrow F \in (MNP) \cap (SBD)\) (3)

\(\left\{ {\begin{array}{*{20}{l}}{N \in (MNP)}\\{N \in SB,SB \subset (SBD)}\end{array}} \right. \Rightarrow N \in (MNP) \cap (SBD)\) (4)

Từ (3) và (4) suy ra \((MNP) \cap (SBD) = NF\).

b) Gọi \(Q = NF \cap SD\) (vì \(NF,SD \subset (SBD)\)).

Ta có \(\left\{ {\begin{array}{*{20}{l}}{Q \in SD}\\{Q \in NF,NF \subset (MNP)}\end{array}} \right. \Rightarrow Q = SD \cap (MNP)\).

c) Ta có \(\left\{ {\begin{array}{*{20}{l}}{H = MN \cap PQ,MN \subset (SAB),PQ \subset (SCD) \Rightarrow H \in (SAB) \cap (SCD)}&{(*)}\\{E = AB \cap CD,AB \subset (SAB),CD \subset (SCD) \Rightarrow E \in (SAB) \cap (SCD)}&{(**)}\\{S \in (SAB) \cap (SCD)}&{(***)}\end{array}} \right.\)

Từ (*), (**), (**) suy ra ba điểm S, H, E thuộc giao tuyến của hai mặt phẳng (SAB) và (SCD) nên ba điểm S, H, E thẳng hàng.

d) Gọi \(G = MQ \cap NP\) (vì \(MQ,NP \subset (MNP))\) (5)

\(\left\{ \begin{array}{l}G \in MQ,MQ \subset (SAD)\\G \in NP,NP \subset (SBC)\end{array} \right. \Rightarrow G \in (SAD) \cap (SBC)\) (6)

Ngoài ra \((SAD) \cap (SBC) = SK \Rightarrow G \in SK\) (7)

Từ (5), (6), (7) suy ra ba đường thẳng SK, QM, NP đồng quy.