Hai đường thẳng song song - Từ điển môn Toán 11 1. Vị trí tương đối của hai đường thẳng trong không gian
Cho hai đường thẳng phân biệt a và b trong không gian. Khi đó, chỉ xảy ra một trong các trường hợp sau:
TH1: Có một mặt phẳng chứa a và b. Khi đó a và b đồng phẳng. Có hai khả năng xảy ra:
+ a và b cắt nhau tại điểm duy nhất I, kí hiệu \(a \cap b = \{ I\} \) hoặc \(a \cap b = I\).
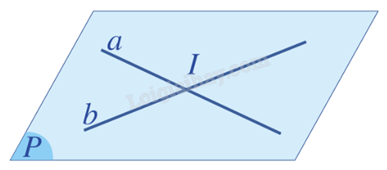
+ a và b song song với nhau, kí hiệu a // b.
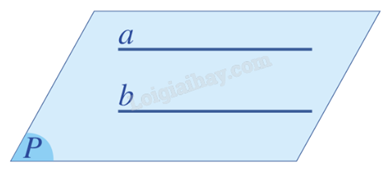
TH2: Không có mặt phẳng nào chứa a và b. Khi đó a và b chéo nhau.
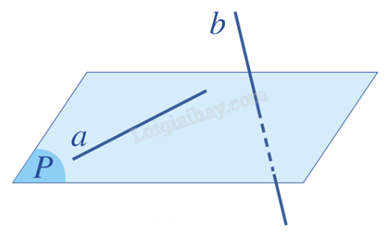
2. Ví dụ minh hoạ về vị trí tương đối của hai đường thẳng trong không gian
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Hãy xét vị trí tương đối của mỗi cặp đường thẳng sau: AB và CD; SA và BC.
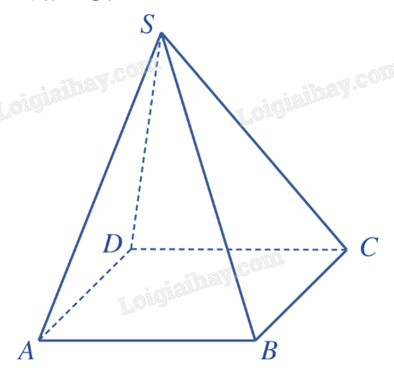
Giải:
Tứ giác ABCD là hình bình hành nên AB và CD song song với nhau.
Do bốn điểm S, A, B, C không cùng nằm trên một mặt phẳng nên hai đường thẳng SA và BC chéo nhau.
