Cách tìm giao điểm của đường thẳng và mặt phẳng - Toán 11

Muốn tìm giao điểm của đường thẳng d và mặt phẳng (P), ta có hai cách làm:

Cách 1: Những bài toán đơn giản, có sẵn một mặt phẳng (Q) chứa đường thẳng d và một đường thẳng a thuộc mặt phẳng (P). Giao điểm của hai đường thẳng không song song d và a chính là giao điểm của đường thẳng d và mặt phẳng (P).

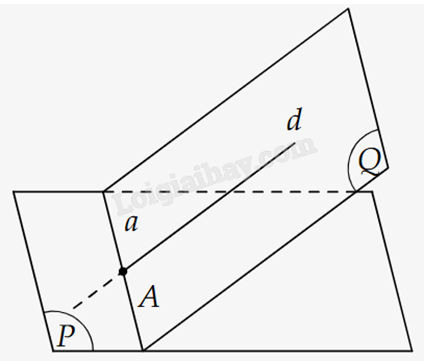
Cách 2: Tìm một mặt phẳng (Q) chứa đường thẳng d, sao cho dễ dàng tìm giao tuyến a với mặt phẳng (P) chính là giao điểm của đường thẳng d và giao tuyến a vừa tìm.

1) Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AC và BC. K là điểm nằm trên BD sao cho KD < KB. Tìm giao điểm của CD và AD với mặt phẳng (MNK).

Giải:

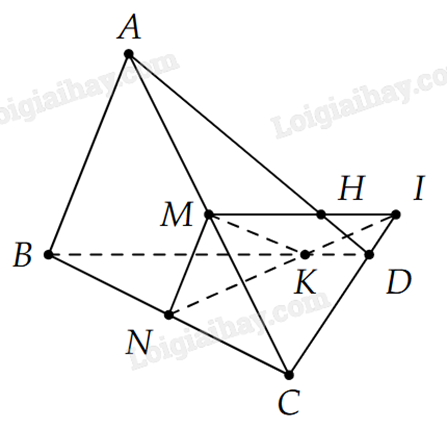
*) Tìm giao điểm của CD với (MNK).

Để ý CD và NK cùng thuộc mặt phẳng (BCD) và chúng không song song nên hai đường thẳng này sẽ cắt nhau tại một điểm I, nhưng NK lại thuộc mp(MNK) suy ra I thuộc mp(MNK).

Vậy I chính là giao điểm của CD và mp(MNK).

Ta có thể trình bày lời giải như sau:

Trong mặt phẳng (BCD), gọi \(I = CD \cap NK\).

\(\left\{ {\begin{array}{*{20}{l}}{I \in CD}\\{I \in NK,NK \subset (MNK)}\end{array}} \right. \Rightarrow I = CD \cap (MNK)\).

*) Tìm giao điểm của AD và (MNK).

Chọn mặt phẳng (ADC) chứa AD. Sau đó tìm giao tuyến của (ACD) và (MNK), ta trình bày như sau:

\(\left\{ {\begin{array}{*{20}{l}}{M \in (MNK)}\\{M \in AC,AC \subset (ACD)}\end{array}} \right. \Rightarrow M \in (MNK) \cap (ACD)\).

\(\left\{ {\begin{array}{*{20}{l}}{I \in NK,NK \subset (MNK)}\\{I \in CD,CD \subset (ACD)}\end{array}} \right. \Rightarrow I \in (MNK) \cap (ACD)\).

Vậy \((MNK) \cap (ACD) = MI\). Gọi \(H = MI \cap AD\). Suy ra \(H = AD \cap (MNK)\).

2) Cho tứ diện ABCD. Trên AB, AC, BD lấy lần lượt ba điểm M, N, P sao cho MN không song song với BC, MP không song song với AD. Xác định giao điểm của các đường thẳng BC, AD, CD với mặt phẳng (MNP).

Giải:

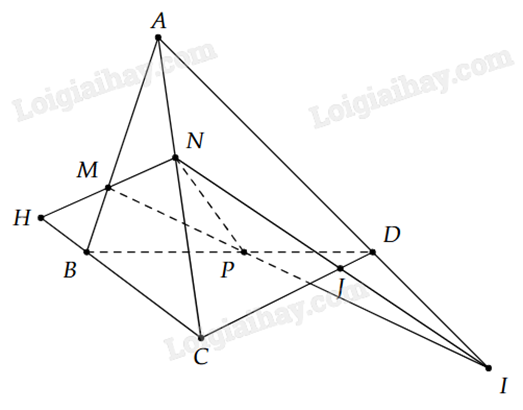
*) Tìm giao điểm của BC và (MNP).

Trong (ABC), gọi \(H = MN \cap BC\).

\(\left\{ {\begin{array}{*{20}{l}}{H \in BC}\\{H \in MN,MN \subset (MNP)}\end{array}} \right. \Rightarrow H \in BC \cap (MNP)\).

*) Tìm giao điểm của AD và (MNP).

Trong (ACD), gọi \(I = MP \cap AD\).

\(\left\{ {\begin{array}{*{20}{l}}{I \in AD}\\{I \in MP,MP \subset (MNP)}\end{array}} \right. \Rightarrow I \in AD \cap (MNP)\).

*) Tìm giao điểm của CD và (MNP).

\(\left\{ {\begin{array}{*{20}{l}}{I \in AD,AD \subset (ACD)}\\{N \in AC,AC \subset (ACD)}\end{array}} \right. \Rightarrow IN \subset (ACD)\).

Trong (ACD), gọi \(J = NI \cap CD\).

\(\left\{ {\begin{array}{*{20}{l}}{J \in CD}\\{I \in NI,NI \subset (MNP)}\end{array}} \right. \Rightarrow J = CD \cap (MNP)\).