1. Cách giải bài toán thực tế ứng dụng nguyên hàm
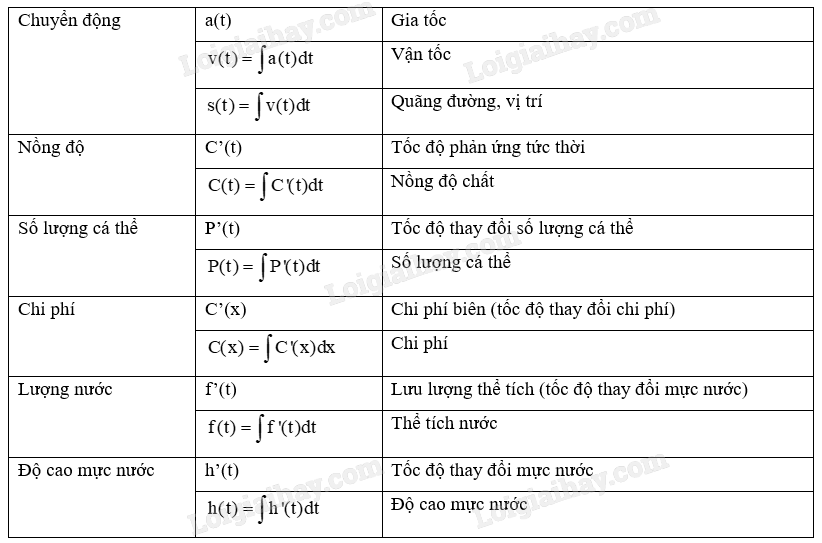
2. Ví dụ minh hoạ về giải bài toán thực tế ứng dụng nguyên hàm
1) Một quần thể vi sinh vật có tốc độ tăng số lượng cá thể được ước lượng bởi \(P'\left( t \right) = 150\sqrt t \) (cá thể/ngày) với \(0 \le t \le 10\), trong đó \(P\left( t \right)\) là số lượng cá thể vi sinh vật tại thời điểm \(t\) ngày kể từ thời điểm ban đầu. Biết rằng ban đầu quần thể có 1000 cá thể.
a) Xác định hàm số \(P\left( t \right)\).
b) Ước lượng số cá thể của quần thể sau 5 ngày kể từ thời điểm ban đầu (kết quả làm tròn đến hàng trăm).
Giải:
a) \(P\left( t \right) = \int {P'\left( t \right)dt} {\rm{\;}} = \int {150\sqrt t dt} {\rm{\;}} = \int {150{t^{\frac{1}{2}}}dt} {\rm{\;}} = 150.\frac{{{t^{\frac{3}{2}}}}}{{\frac{3}{2}}} + C = 100t\sqrt t {\rm{\;}} + C\).
Theo đề bài ta có \(P\left( 0 \right) = 1000 \Leftrightarrow 100.0\sqrt 0 {\rm{\;}} + C = 1000 \Leftrightarrow C = 1000\).
Vậy \(P\left( t \right) = 100t\sqrt t {\rm{\;}} + 1000\).
b) \(P\left( 5 \right) = 100.5\sqrt 5 {\rm{\;}} + 1000 = 500\sqrt 5 {\rm{\;}} + 1000 \approx 2100\) (cá thể).
2) Một vật chuyển động thẳng dọc theo một đường thẳng (có gắn trục toạ độ Ox, với độ dài đơn vị bằng 1 m). Biết rằng vật xuất phát từ vị trí ban đầu là gốc toạ độ và chuyển động với vận tốc v(t) = 8 – 0,4t (m/s) trong đó t là thời gian tính theo giây \(\left( {t \ge 0} \right)\).
a) Xác định toạ độ \(x\left( t \right)\) của vật tại thời điểm \(t,t \ge 0\).
b) Tại thời điểm nào thì vật đi qua gốc toạ độ (không tính thời điểm ban đầu)?
Giải:
a) \(x\left( t \right) = \int {v\left( t \right)dt} {\rm{\;}} = \int {\left( {8 - 0,4t} \right)dt} {\rm{\;}} = 8t - 0,2{t^2} + C\).
Do vật xuất phát từ vị trí ban đầu là gốc toạ độ nên \(x\left( 0 \right) = 0 \Leftrightarrow 8.0 - 0,{2.0^2} + C = 0 \Leftrightarrow C = 0\).
Vậy \(x\left( t \right) = 8t - 0,2{t^2}\).
b) Vật đi qua gốc toạ độ khi \(x\left( t \right) = 0 \Leftrightarrow 8t - 0,2{t^2} = 0 \Leftrightarrow t = 0\) hoặc \(t = 40\).
Vậy vật đi qua gốc toạ độ tại thời điểm \(t = 40\) giây (không tính thời điểm ban đầu).
3) Một viên đạn được bắn thẳng đứng lên trên từ mặt đất với vận tốc tại thời điểm t (t = 0 là thời điểm viên đạn được bắn lên) cho bởi v(t) = 150 - 9,8t (m/s).
Tìm độ cao của viên đạn (tính từ mặt đất):
a) Sau t = 3 giây.
b) Khi nó đạt độ cao lớn nhất (làm tròn kết quả đến chữ số thập phân thứ nhất của mét).
Giải:
a) Độ cao \(h\left( t \right)\) của viên đạn tại thời điểm \(t\) là một nguyên hàm của hàm vận tốc \(v\left( t \right)\).
Ta có \(h\left( t \right) = \int {\left( {150 - 9,8t} \right)} dt = 150t - 4,9{t^2} + C\).
Do \(t = 0\) là thời điểm viên đạn được bắn lên nên \(h\left( 0 \right) = 0\).
Suy ra \(150 \cdot 0 - 4,9 \cdot {0^2} + C = 0 \Leftrightarrow C = 0 \Leftrightarrow \)\(h\left( t \right) = 150t - 4,9{t^2}\).
Độ cao của viên đạn sau 3 giây là \(h\left( 3 \right) = 150 \cdot 3 - 4,9 \cdot {3^2} = 405,9\) (m).
b) Độ cao lớn nhất của viên đạn là giá trị lớn nhất của hàm số \(h\left( t \right) = 150t - 4,9{t^2}\) với \(t \ge 0\).
Ta có \(h'\left( t \right) = 150 - 9,8t\) suy ra \(h'\left( t \right) = 0 \Leftrightarrow 150 - 9,8t = 0 \Leftrightarrow t = \frac{{750}}{{49}}\).
Ta lập bảng biến thiên:
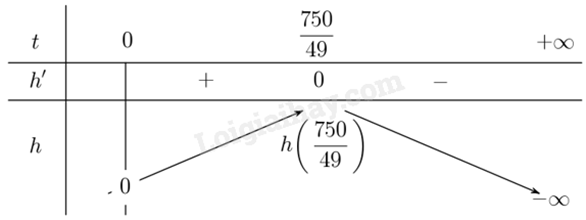
Từ bảng biến thiên suy ra \(\mathop {\max }\limits_{\left[ {0; + \infty } \right)} h\left( t \right) = h\left( {\frac{{750}}{{49}}} \right) = \frac{{56250}}{{49}} \approx 1147,96\).
Vậy viên đạt đạt độ cao lớn nhất khoảng $1147,96$ m tại thời điểm \(t = \frac{{750}}{{49}}\) giây.

 Nguyên hàm - Từ điển môn Toán 12
Nguyên hàm - Từ điển môn Toán 12 






Danh sách bình luận