Cách giải bài toán thực tế ứng dụng tích phân - Toán 12

Quãng đường đi được trong khoảng thời gian t = a đến t = b: \(s = \int\limits_a^b {v(t)dt} \).

1) Một ôtô đang dừng và bắt đầu chuyển động theo một đường thẳng với gia tốc a(t) = 6 – 2t \((m/{s^2})\), trong đó t là khoảng thời gian tính bằng giây kể từ lúc ôtô bắt đầu chuyển động. Hỏi quãng đường ôtô đi được kể từ lúc bắt đầu chuyển động đến khi vận tốc của ôtô đạt giá trị lớn nhất là bao nhiêu mét?

Giải:

\(v(t) = \int {a(t)dt}  = \int {\left( {6 - 2t} \right)dt}  = 6t - {t^2} + C\).

Vì ở thời điểm t = 0 thì ô tô dang dừng nên ta có \(v(0) = 0 \Leftrightarrow 6.0 - {0^2} + C = 0 \Leftrightarrow C = 0\).

Suy ra \(v(t) = 6t - {t^2}\).

\(s(t) = \int {v(t)dt}  = \int {\left( {6t - {t^2}} \right)dt}  = 3{t^2} - \frac{{{t^3}}}{3} + C'\).

Vì ở thời điểm t = 0 thì ô tô dang dừng nên ta có \(s(0) = 0 \Leftrightarrow {3.0^2} - \frac{{{0^3}}}{3} + C' = 0 \Leftrightarrow C' = 0\).

Suy ra \(s(t) = 3{t^2} - \frac{{{t^3}}}{3}\).

Xét hàm \(v(t) = 6t - {t^2}\), ta có \(v'(t) = a(t) = 6 - 2t = 0 \Leftrightarrow t = 3\).

Bảng biến thiên:

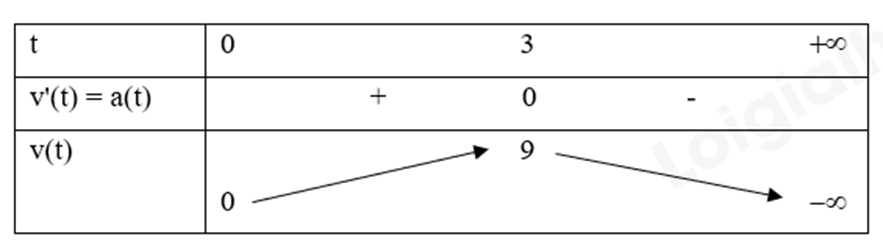
Từ bảng biến thiên suy ra vận tốc ô tô lớn nhất khi t = 3.

Khi đó, quãng đường ô tô chuyển động được là \(s(3) = {3.3^2} - \frac{{{3^3}}}{3} = 18\) (m).

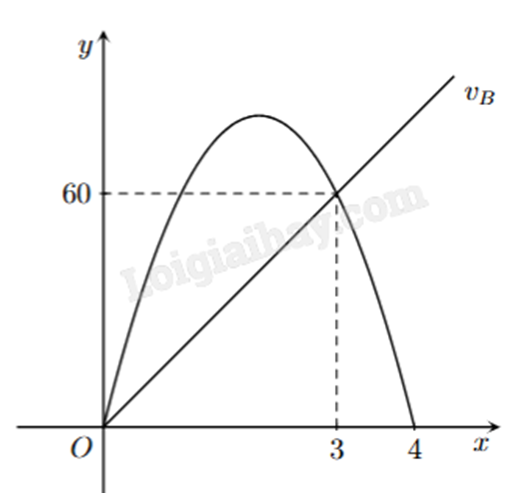
2) Cho đồ thị biểu diễn vận tốc của hai xe A và B khởi hành cùng một lúc và cùng vạch xuất phát, đi cùng chiều trên một con đường. Biết đồ thị biểu diễn vận tốc của xe A là một đường parabol và đồ thị biểu diễn vận tốc của xe B là một đường thẳng như hình vẽ bên. Hỏi sau 5 giây kể từ lúc xuất phát thì khoảng cách giữa hai xe là bao nhiêu mét (làm tròn đến hàng phần chục và biết rằng xe A sẽ dừng lại khi vận tốc bằng 0)?

Giải:

Gọi parabol \({v_A}\) biểu diễn vận tốc xe A có phương trình \(y = {a_A}{x^2} + {b_A}x + c\) và đường thẳng \({v_B}\) biểu diễn vận tốc xe B có phương trình \(y = {a_B}x + {b_B}\).

Parabol \({v_A}\) di qua ba điểm O(0;0), M(3;60) và N(4;0) nên ta có:

\(\left\{ \begin{array}{l}0 = {a_A}{.0^2} + {b_A}.0 + c\\60 = {a_A}{.3^2} + {b_A}.3 + c\\0 = {a_A}{.4^2} + {b_A}.4 + c\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{a_A} =  - 20\\{b_A} = 80\\c = 0\end{array} \right. \Rightarrow y =  - 20{x^2} + 80x\).

\({v_B}\) là đường thẳng đi qua hai điểm O(0;0) và M(3;60) nên \(\left\{ \begin{array}{l}0 = {a_B}.0 + {b_B}\\60 = {a_B}.3 + {b_B}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{b_B} = 0\\{a_B} = 20\end{array} \right. \Rightarrow y = 20x\).

Quãng đường xe A đi được sau 4 giây là \(\int\limits_0^4 {\left( { - 20{x^2} + 80x} \right)dx}  = \frac{{640}}{3}\). Khi x = 4 thì \({v_A} = 0\) nên xe dừng sau 4 giây, đi được quãng đường bằng \(\frac{{640}}{3}\).

Quãng đường xe B đi được sau 5 giây là \(\int\limits_0^5 {20xdx}  = 250\).

Khoảng cách giữa hai xe sau 5 giây là \(250 - \frac{{640}}{3} = \frac{{110}}{3} \approx 36,7\).