1. Vecto pháp tuyến của mặt phẳng là gì?
Nếu vecto \(\overrightarrow n \ne \overrightarrow 0 \) và có giá vuông góc với \(\left( \alpha \right)\) thì \(\overrightarrow n \) được gọi là vecto pháp tuyến của \(\left( \alpha \right)\).
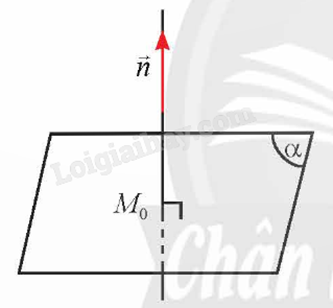
2. Cách xác định vecto pháp tuyến của mặt phẳng
Trong không gian với hệ trục toạ độ Oxyz, cho mặt phẳng (P): Ax + By + Cz + D = 0.
Một vecto pháp tuyến của (P) là \(\overrightarrow n = (A;B;C)\).
Khi đó, với số thực \(k \ne 0\), \(k\overrightarrow n = (kA;kB;kC)\) cũng là một vecto pháp tuyến của (P).
3. Ví dụ minh hoạ
1) Mặt phẳng (P): -2x + 5y + z – 3 = 0 có một vecto pháp tuyến là \(\overrightarrow n = \left( { - 2;5;1} \right)\).
2) Mặt phẳng (Q): x – y + z – 1 = 0 có một vecto pháp tuyến là \(\overrightarrow m = \left( {1; - 1;1} \right)\).
Ta có \(2\overrightarrow m = \left( {2; - 2;2} \right)\) cũng là một vecto pháp tuyến của (Q).

 Phương trình mặt phẳng - Từ điển Toán 12
Phương trình mặt phẳng - Từ điển Toán 12 






Danh sách bình luận