Cách tính diện tích hình phẳng ứng dụng tích phân - Toán 12

Cho hàm số f(x) liên tục trên đoạn [a;b]. Nếu F(x) là một nguyên hàm của f(x) trên đoạn [a;b] thì hiệu số F(b) – F(a) được gọi là tích phân từ a đến b của hàm số f(x).

\(\int\limits_a^b {f(x)dx}  = F(x)\left| {\begin{array}{*{20}{c}}{^b}\\{_a}\end{array}} \right. = F(b) - F(a)\).

Trong đó:

+ \(\int\limits_a^b {} \) là dấu tích phân.

+ a và b là cận tích phân (a là cận dưới, b là cận trên).

+ f(x)dx là biểu thức dưới dấu tích phân.

+ f(x) là hàm số dưới dấu tích phân.

Lưu ý:

+ \(\int\limits_a^a {f(x)dx}  = 0\);

+ \(\int\limits_a^b {f(x)dx}  =  - \int\limits_b^a {f(x)dx} \);

Diện tích S của hình phẳng giới hạn bởi đồ thị của hàm số y = f(x) liên tục trên [a;b], trục hoành và hai đường thẳng x = a, x = b (a < b) được tính bằng công thức

\(S = \int\limits_a^b {\left| {f(x)} \right|dx} \)

Diện tích S của hình phẳng giới hạn bởi đồ thị của hai hàm số y = f(x), g(x) liên tục trên \(\left[ {a;b} \right]\) và hai đường thẳng x = a, x = b được tính bằng công thức

\(S = \int\limits_a^b {\left| {f(x) - g(x)} \right|dx} \)

Ví dụ minh hoạ:

1) Tính diện tích hình phẳng (H) được giới hạn bởi đồ thị hai hàm số \(y = {x^2} - 2\), \(y = x\) và các đường thẳng x = -1, x = 2.

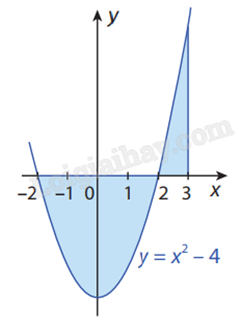
Giải:

Gọi S là diện tích hình phẳng cần tìm. Ta có:

\(S = \int\limits_{ - 2}^3 {\left| {{x^2} - 4} \right|dx}  = S = \int\limits_{ - 2}^2 {\left| {{x^2} - 4} \right|dx}  + S = \int\limits_2^3 {\left| {{x^2} - 4} \right|dx} \)

\(\int\limits_{ - 2}^2 {({x^2} - 4)dx}  + \int\limits_2^3 {({x^2} - 4)dx}  = \left( { - \frac{{{x^3}}}{3} + 4x} \right)\left| {\begin{array}{*{20}{c}}2\\{ - 2}\end{array} + } \right.\left( {\frac{{{x^3}}}{3} - 4x} \right)\left| {\begin{array}{*{20}{c}}3\\2\end{array}} \right. = 13\) (đvdt).

2) Tính diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số \(y = {x^2}\), \(y = 2 - x\) và hai đường thẳng x = 0, x = 2.

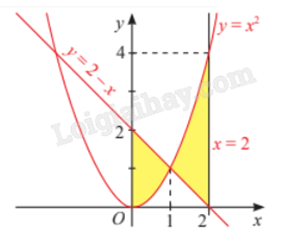
Giải:

Diện tích cần tìm là \(\int\limits_0^2 {\left| {{x^2} - (2 - x)} \right|dx}  = \int\limits_0^2 {\left| {{x^2} + x - 2} \right|dx} \).

Ta có \({x^2} + x - 2 = 0 \Leftrightarrow \) x = 1 hoặc x = -2.

Vậy \(S = \int\limits_0^1 {\left| {{x^2} + x - 2} \right|dx}  + \int\limits_1^2 {\left| {{x^2} + x - 2} \right|dx}  = \left| {\int\limits_0^1 {\left( {{x^2} + x - 2} \right)dx} } \right| + \left| {\int\limits_1^2 {\left( {{x^2} + x - 2} \right)dx} } \right|\)

\( = \left| {\left( {\frac{{{x^3}}}{3} + \frac{{{x^2}}}{2} - 2x} \right)\left| {\begin{array}{*{20}{c}}1\\0\end{array}} \right.} \right| + \left| {\left( {\frac{{{x^3}}}{3} + \frac{{{x^2}}}{2} - 2x} \right)\left| {\begin{array}{*{20}{c}}2\\1\end{array}} \right.} \right| = \left| { - \frac{7}{6}} \right| + \left| {\frac{{11}}{6}} \right| = 3\).