Cách tính thể tích khối tròn xoay ứng dụng tích phân - Toán 12

Cho hàm số f(x) liên tục trên đoạn [a;b]. Nếu F(x) là một nguyên hàm của f(x) trên đoạn [a;b] thì hiệu số F(b) – F(a) được gọi là tích phân từ a đến b của hàm số f(x).

\(\int\limits_a^b {f(x)dx}  = F(x)\left| {\begin{array}{*{20}{c}}{^b}\\{_a}\end{array}} \right. = F(b) - F(a)\).

Trong đó:

+ \(\int\limits_a^b {} \) là dấu tích phân.

+ a và b là cận tích phân (a là cận dưới, b là cận trên).

+ f(x)dx là biểu thức dưới dấu tích phân.

+ f(x) là hàm số dưới dấu tích phân.

Lưu ý:

+ \(\int\limits_a^a {f(x)dx}  = 0\);

+ \(\int\limits_a^b {f(x)dx}  =  - \int\limits_b^a {f(x)dx} \);

a) Khối tròn xoay quanh trục Ox

Cho hàm số f(x), g(x) liên tục, không âm trên đoạn \(\left[ {a;b} \right]\).

Thể tích của khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi đồ thị hàm số y = f(x), trục hoành và hai đường thẳng x = a, x = b quanh trục Ox là

\(V = \pi \int\limits_a^b {{f^2}(x)dx} \)

Thể tích của khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi đồ thị hàm số y = f(x), g(x) và hai đường thẳng x = a, x = b quanh trục Ox là

\(V = \pi \int\limits_a^b {\left| {{f^2}(x) - {g^2}(x)} \right|dx} \)

b) Khối tròn xoay quanh trục Oy

Cho hàm số f(x), g(x) liên tục với mọi \(y \in [c,d]\).

Thể tích của khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi đồ thị hàm số x = f(y), trục tung và hai đường thẳng y = c, y = d quanh trục Oy là

\(V = \pi \int\limits_c^d {{f^2}(y)dy} \)

Thể tích của khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi đồ thị hàm số x = f(y), x = g(y) và hai đường thẳng y = c, y = d quanh trục Oy là

\(V = \pi \int\limits_a^b {\left| {{f^2}(y) - {g^2}(y)} \right|dy} \)

Ví dụ minh hoạ:

1) Tính thể tích của khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường thẳng quay quanh trục hoành \(y = {x^2} - 2x\), y = 0, x = 2.

Giải:

Thể tích khối tròn xoay là:

\(V = \pi \int\limits_0^2 {{{({x^2} - 2x)}^2}dx}  = \pi \int\limits_0^2 {({x^4} - 4{x^3} + 4{x^2})dx} \)

\( = \pi \left( {\frac{{{x^5}}}{5} - {x^4} + \frac{4}{3}{x^3}} \right)\left| {\begin{array}{*{20}{c}}2\\0\end{array}} \right. = \frac{{16\pi }}{{15}}\) (đvdt).

2) Hình vẽ mô phòng phần bên trong của một chậu cây có dạng khối tròn xoay tạo thành khi quay một phần của đồ thị hàm số \(y = \sqrt x  + \frac{3}{2}\)​ với \(0 \le x \le 4\) quanh trục hoành. Tính thể tích phần bên trong (dung tích) của chậu cây, biết đơn vị trên các trục Ox, Oy là decimét.

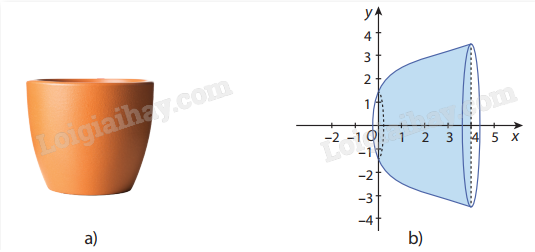
Giải:

Thể tích phần trong của chậu cây là:

\(V = \pi \int\limits_0^4 {{{\left( {\sqrt x  + \frac{3}{2}} \right)}^2}dx}  = \pi \int\limits_0^4 {{{\left( {x + 3{x^{\frac{1}{2}}} + \frac{9}{4}} \right)}^2}dx}  = \pi \left( {\frac{{{x^2}}}{2} + 2{x^{\frac{3}{2}}} + \frac{9}{4}x} \right)\left| {\begin{array}{*{20}{c}}4\\0\end{array}} \right. = 33\pi \) (\(d{m^3}\)).