Cách tính tích phân bằng máy tính Casio - Toán 12

Để tính tích phân xác định \(\int\limits_a^b {f(x)dx} \) ta thực hiện các thao tác sau:

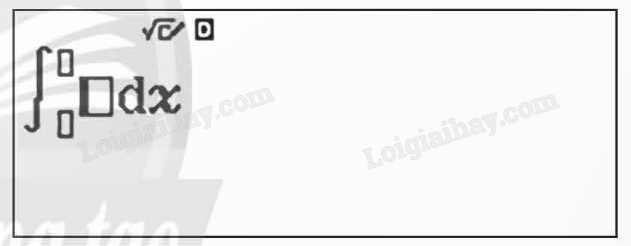
B1: Ấn phím để chọn phép toán tích phân xác định:

B2: Nhập hàm số f(x).

B3: Nhập hai cận tích phân: a, b.

B4: Nhấn “=” để tính giá trị gần đúng của tích phân xác định.

1) Tính gần đúng \(\int\limits_{ - 1}^5 {({x^3} - 3x)dx} \).

Mở máy tính và ấn phím chọn phép toán tích phân xác định:

Nhập hàm số và hai cận:

Ta được kết quả \(\int\limits_{ - 1}^5 {({x^3} - 3x)dx}  = 120\):

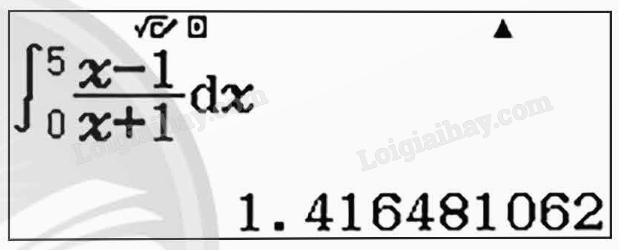
2) Tính gần đúng \(\int\limits_0^5 {\frac{{x - 1}}{{x + 1}}dx} \).

Mở máy tính và ấn phím chọn phép toán tích phân xác định:

Nhập hàm số và hai cận:

Ta được kết quả \(\int\limits_0^5 {\frac{{x - 1}}{{x + 1}}dx}  \approx 1,416481062\):

3) Tính gần đúng \(\int\limits_{0,5}^4 {\frac{{{x^2} - x - 1}}{{x + 1}}dx} \).

Mở máy tính và ấn phím chọn phép toán tích phân xác định:

Nhập hàm số và hai cận:

Ta được kết quả \(\int\limits_{0,5}^4 {\frac{{{x^2} - x - 1}}{{x + 1}}dx}  \approx 1,177585093\):