Tìm các giá trị của tham số m để phương trình $\dfrac{1}{2}{x^2} - 4\left| x \right| + 3 = {m^2}$ có 3 nghiệm thực phân biệt.
-
A.
$m = 3$
-
B.
$ - \sqrt 3 < m < \sqrt 3 $
-
C.
$m = \pm \sqrt 3 $
-
D.
Không tồn tại
- Vẽ đồ thị hàm số \(y = \dfrac{1}{2}{x^2} - 4x + 3\).
- Dựng đồ thị hàm số $y = \dfrac{1}{2}{x^2} - 4\left| x \right| + 3$ có được từ đồ thị hàm số vừa vẽ: Giữ nguyên phần đồ thị bên phải trục tung, xóa bỏ phần bên trái trục tung đồng thời lấy đối xứng phần đồ thị đó qua trục tung.
Phương trình $\dfrac{1}{2}{x^2} - 4\left| x \right| + 3 = {m^2}$ có 3 nghiệm thực phân biệt khi đồ thị hàm số $y=\dfrac{1}{2}{x^2} - 4\left| x \right| + 3$ cắt đồ thị hàm số $y=m^2$ tại 3 điểm phân biệt.
Ta vẽ đồ thị của hai hàm số trên.
Đồ thị hàm số $y = \dfrac{1}{2}{x^2} - 4\left| x \right| + 3$ được vẽ như sau:
+ Vẽ đồ thị hàm số $y = \dfrac{1}{2}{x^2} - 4x + 3$.
+ Giữ nguyên nhánh bên phải trục tung của đồ thị hàm $y = \dfrac{1}{2}{x^2} - 4x + 3$ và xóa nhánh bên trái trục tung.
+ Lấy đối xứng phần đồ thị bên phải qua trục tung.
Ta được đồ thị hàm số $\dfrac{1}{2}{x^2} - 4\left| x \right| + 3 = {m^2}$ như hình dưới.
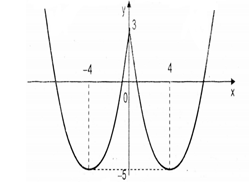
Đồ thị hàm số $y=m^2$ là một đường thẳng song song với trục hoành.
Để hai đồ thị trên cắt nhau tại 3 điểm thì vị trí của đường thẳng $y=m^2$ như sau:
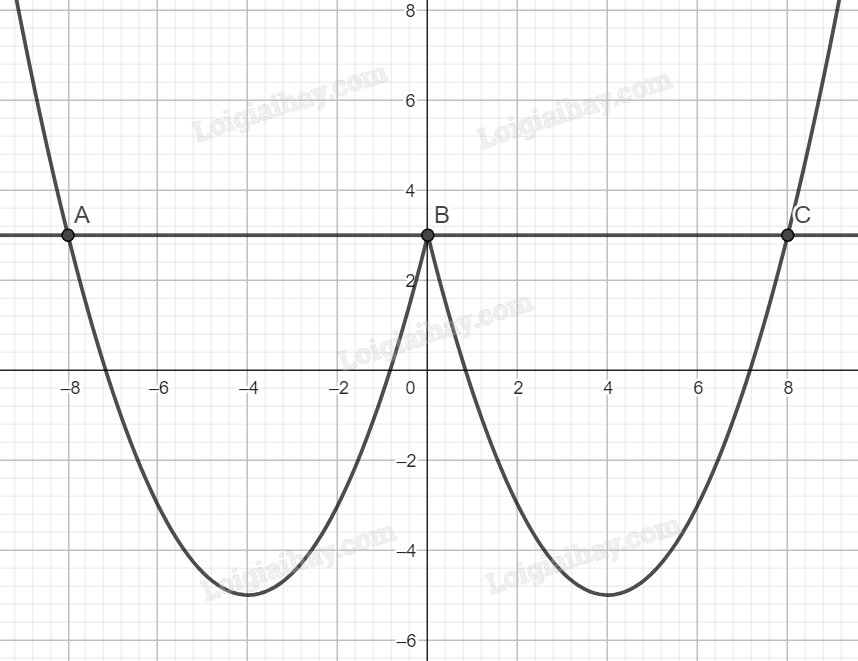
Khi đó $y={m^2} = 3 \Leftrightarrow m = \pm \sqrt 3 $.
Đáp án : C
Các bài tập cùng chuyên đề
Cho đồ thị hàm số $y = a{x^2} + bx + c\,$như hình vẽ.
Khẳng định nào sau đây là đúng:
Xác định Parabol $\left( P \right):\,\,y = a{x^2} + bx + 2$ biết rằng Parabol đi qua hai điểm $M\left( {1;\,\,5} \right)$ và $N\left( {2;\,\, - 2} \right)$.
Xác định Parabol $\left( P \right):\,\,y = a{x^2} + bx - 5$ biết rằng Parabol đi qua điểm $A\left( {3;\,\, - 4} \right)$ và có trục đối xứng $x = - \dfrac{3}{2}$.
Xác định Parabol $\left( P \right):\,\,y = a{x^2} + bx + 3$ biết rằng Parabol có đỉnh $I\left( {3;\,\, - 2} \right)$.
Viết phương trình của Parabol $(P)$ biết rằng $(P)$ đi qua các điểm $A\left( {0;\,\,2} \right),\,\,B\left( { - 2;\,\,5} \right),\,\,C\left( {3;\,\,8} \right)$
Tìm các giá trị của tham số $m$ để phương trình $2{x^2} - 2x + 1 - m = 0$ có hai nghiệm phân biệt
Tìm các giá trị thực của tham số $m$ để phương trình $\left| {{x^2} - 3x + 2} \right| = m$ có bốn nghiệm thực phân biệt.
Tìm các giá trị của $m$ để phương trình ${x^2} - 2x + \sqrt {4{x^2} - 12x + 9} = m$ có nghiệm duy nhất.
Cho phương trình của $\left( P \right):\,\,y = a{x^2} + bx + c\,\,\left( {a \ne 0} \right)$ biết rằng hàm số có giá trị lớn nhất bằng 1 và đồ thị hàm số đi qua các điểm $A\left( {2;\,\,0} \right),\,\,B\left( { - 2;\,\, - 8} \right)$. Tình tổng ${a^2} + {b^2} + {c^2}$.
Biết đồ thị hàm số $\left( P \right):\,\,y = {x^2} - \left( {{m^2} + 1} \right)x - 1$ cắt trục hoành tại hai điểm phân biệt có hoành độ \({x_1},{x_2}.\) Tìm giá trị của tham số $m$ để biểu thức $T = {x_1} + {x_2}$ đạt giá trị nhỏ nhất.
Tìm các giá trị của tham số $m$ để phương trình ${x^2} - 2\left( {m + 1} \right)x + 1 = 0$ có hai nghiệm phân biệt trong đó có đúng một nghiệm thuộc khoảng $\left( {0;\,\,1} \right)$.
Tìm các giá trị của tham số $m$ để $2{x^2} - 2\left( {m + 1} \right)x + {m^2} - 2m + 4 \ge 0 \left( {\forall x} \right)$
Tìm giá trị nhỏ nhất của hàm số $f\left( x \right)$ biết rằng $f\left( {x + 2} \right) = {x^2} - 3x + 2$ trên $\mathbb{R}$
Cho hàm số $f\left( x \right) = {x^2} + 2x - 3$.
Xét các mệnh đề sau:
i) $f\left( {x - 1} \right) = {x^2} - 4$
ii) Hàm số đã cho đồng biến trên $\left( { - 1;\,\, + \infty } \right)$
iii) Giá trị nhỏ nhất của hàm số là một số âm.
iv) Phương trình $f\left( x \right) = m$ có nghiệm khi $m \ge - 4$
Số mệnh đề đúng là:
Tìm các giá trị của m để hàm số $y = {x^2} + mx + 5$ luôn đồng biến trên $\left( {1;\,\, + \infty } \right)$.
Tìm giá trị của $m$ để hàm số $y = - {x^2} + 2x + m - 5$ đạt giá trị lớn nhất bằng $6$
Tìm giá trị của m để đồ thị hàm số $y = {x^2} - 2x + m - 1$ cắt trục hoành tại hai điểm phân biệt có hoành độ dương.
Tìm điểm $A$ cố định mà họ đồ thị hàm số $y = {x^2} + \left( {2 - m} \right)x + 3m\,\,\left( {{P_m}} \right)$ luôn đi qua.
Tìm giá trị nhỏ nhất của biểu thức $P = 3\left( {\dfrac{{{a^2}}}{{{b^2}}} + \dfrac{{{b^2}}}{{{a^2}}}} \right) - 8\left( {\dfrac{a}{b} + \dfrac{b}{a}} \right)$.
Một chiếc cổng parabol dạng \(y = \dfrac{{ - 1}}{2}{x^2}\) có chiều rộng \(d = 8m.\) Hãy tính chiều cao \(h\) của cổng ?
