Tìm các giá trị của tham số $m$ để phương trình $2{x^2} - 2x + 1 - m = 0$ có hai nghiệm phân biệt
-
A.
$m > \dfrac{1}{2}$
-
B.
$m = \dfrac{1}{2}$
-
C.
$m < \dfrac{1}{2}$
-
D.
Không tồn tại
- Tách \(m = 2{x^2} - 2x + 1\), vẽ đồ thị hàm số \(y = 2{x^2} - 2x + 1\).
- Số giao điểm của hai đồ thị hàm số chính là số nghiệm của phương trình.
$2{x^2} - 2x + 1 - m = 0 \Leftrightarrow 2{x^2} - 2x = m - 1$
Số nghiệm của phương trình đã cho bằng số giao điểm của Parabol $\left( P \right):\,\,y = 2{x^2} - 2x$ và đường thẳng $y = m - 1$ có tính chất song song với trục hoành.
Parabol (P) có tọa độ đỉnh \(\left( { - \dfrac{b}{{2a}}; - \dfrac{\Delta }{{4a}}} \right) = \left( {\dfrac{1}{2}; - \dfrac{1}{2}} \right)\)
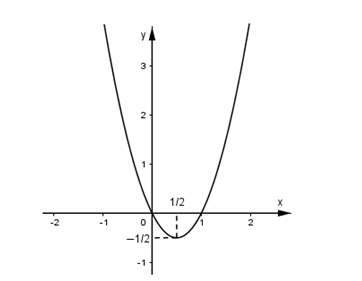
Dựa trên đồ thị ta thấy phương trình đã cho có hai nghiệm khi và chỉ khi $m - 1 > - \dfrac{1}{2} \Leftrightarrow m > \dfrac{1}{2}$
Đáp án : A
Các em có thể sử dụng luôn điều kiện để phương trình bậc hai có hai nghiệm phân biệt, đó là \(\Delta > 0\)








Danh sách bình luận