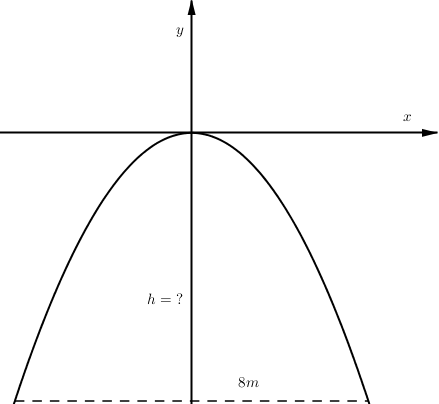
Một chiếc cổng parabol dạng \(y = \dfrac{{ - 1}}{2}{x^2}\) có chiều rộng d = 8m. Hãy tính chiều cao h của cổng.
-
A.
h = 8 (m)
-
B.
h = 7 (m)
-
C.
h = 9 (m)
-
D.
h = 5 (m)
Tìm tọa độ chân cổng. Từ đó ta có chiều cổng bằng trị tuyệt đối tung độ chân cổng.
Khoảng cách từ chân cổng đến trục đối xứng Oy là \(\dfrac{8}{2} = 4\). Hoành độ 2 chân cổng là -4 và 4.
Tung độ chân cổng là \(y = \dfrac{{ - 1}}{2}{.4^2} = - 8\).
Chiều cao của cổng là |-8| = 8 (m).
Đáp án : A
Parabol $y = ax^2$
Đây là phương trình của một parabol có đỉnh nằm tại gốc tọa độ (0;0).
Trục đối xứng của parabol này là trục Oy (đường thẳng x = 0).
Nếu hệ số (a < 0) (như trong trường hợp này, $a = -\frac{1}{2}$), parabol sẽ mở bề lõm xuống dưới. Điều này phù hợp với hình dạng của một chiếc cổng vòm.
Vì parabol đối xứng qua trục Oy, điều này có nghĩa là khoảng cách từ trục Oy đến mỗi "chân" của cổng (điểm parabol chạm đất hoặc mặt phẳng đặt cổng) là bằng nhau. Khoảng cách này là một nửa chiều rộng.
Chiều cao h của cổng chính là khoảng cách thẳng đứng từ đỉnh (tại y = 0) đến mặt phẳng đặt chân cổng. Để tìm vị trí của mặt phẳng này (tức là tung độ y của chân cổng), ta thay một trong các giá trị hoành độ của chân cổng vào phương trình parabol. Kết quả y sẽ giống nhau do tính chất đối xứng.

Các bài tập cùng chuyên đề
Luyện tập – vận dụng 4 trang 43 SGK Toán 10 tập 1 – Cánh diều
Trong bài toán ở phần mở đầu, độ cao y (m) của một điểm thuộc vòng cung thành cầu cảng Sydney đạt giá trị lớn nhất là bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?

Vận dụng trang 55 SGK Toán 10 tập 1 – Chân trời sáng tạo
Trong bài toán ứng dụng, khi chơi trên sân cầu lông đơn, các lần phát cầu với thông tin như sau có được xem là hợp lệ không? (Các thông tin không được đề cập thì vẫn giữ như trong giả thiết bài toán trên)
a) Vận tốc xuất phát của cầu là 12 m/s
b) Vị trí phát cầu cách mặt đất 1,3 m.
Lưu ý: Các thông số về sân cầu lông đơn được cho trong Hình 11.

Bố bạn Lan gửi 10 triệu đồng vào 1 ngân hàng với lãi suất x%/ tháng. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi tháng, số tiền lãi sẽ được nhập với vốn ban đầu để tính lãi cho tháng tiếp theo. Tính số tiền cả vốn và lãi mà bố bạn Lan có được sau khi gửi tiết kiệm 2 tháng?
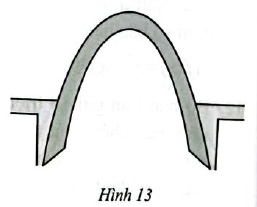
Trong một công trình, người ta xây dựng một cổng ra vào hình parabol (minh họa ở Hình 13) sao cho khoảng cách giữa hai chân cổng BC là 9 m. Từ một điểm M trên thân cổng người ta đo được khoảng cách tới mặt đất là MK = 1,6 m và khoảng cách từ K tới chân cổng gần nhất là BK = 0,5 m. Tính chiều cao của cổng theo đơn vị mét (làm tròn kết quả đến hàng phần mười).
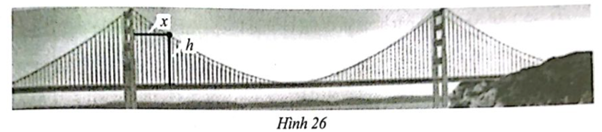
Quan sát chiếc Cổng Vàng (Golden Gate bridge) ở Hình 26. Độ cao \(h\) (feet) tính từ mặt cầu đến các điểm trên dây treo ở phần giữa hai trụ cầu được xác định bởi công thức \(h\left( x \right) = \frac{1}{{9000}}{x^2} - \frac{7}{{15}}x + 500\), trong đó \(x\) (feet) là khoảng cách từ trụ cầu bên trái đến điểm tương ứng trên dây treo.
a) Xác định độ cao của trụ cầu so với mặt cầu theo đơn vị feet.
b) Xác định khoảng cách giữa hai trụ cầu theo đơn vị feet, biết rằng hai trụ cầu này có độ cao bằng nhau.
Giả sử hàm số bậc hai mô phỏng vòm phía trong một trụ của cầu nhật tân là:
\(y = f\left( x \right) = - \frac{{187}}{{856}}{x^2} + \frac{{8041}}{{856}}x\) (đơn vị đo: mét)
a) Hãy tính chiêu dài đoạn dây dọi sử dụng nếu khoảng cách từ chân của trụ cầu đễn quả nặng là 30 cm
b) Hãy tính khoảng cách từ chân trụ cầu đến quả nặng nếu biết chiều dài đoạn dây dọi sử dụng là 15 m
Ta có bảng giá trị của hàm cầu đối với sản phẩm A theo đơn giá của sản phẩm A như sau:
|
Đơn giá sản phẩm A (đơn vị: Nghìn đồng) |
10 |
20 |
40 |
70 |
90 |
|
Lượng cầu (nhu cầu về số sản phẩm) |
338 |
288 |
200 |
98 |
50 |
a) Giả sử hàm cầu là một hàm số bậc hai theo đơn giá x, hãy viết công thức của hàm này, biết rằng \(c = 392\)
b) Chứng tỏ rằng hàm số có thể viết thành dạng \(y = f\left( x \right) = a{\left( {b - x} \right)^2}\)
c) Giả sử hàm cầu này lấy mọi giá trị trên đoạn \(\left[ {0;100} \right]\), hãy tính lượng cầu khi đơn giá sản phẩm A là 30, 50, 100
d) Cùng giả thiết với câu c) nếu lượng cầu là 150 sản phẩm thì đơn giá sản phẩm A là khoảng bao nhiêu (đơn vị: nghìn đồng)
Khi một vật từ vị trí \({y_0}\) được ném xiên lên cao theo góc \(\alpha \) (so với phương ngang) với vận tốc ban đầu \({v_0}\) thì phương trình chuyển động của vật này là:
\(y = \frac{{ - g{x^2}}}{{2v_0^2{{\cos }^2}\alpha }} + \tan \alpha .x + {y_0}\)
a) Vật bị ném xiên như vậy có chuyển động theo đường xiên không? Tại sao?
b) Giả sử góc ném có số đo là \(45^\circ \), vận tốc ban đầu của vật là \(3\)m/s và vật được ném xiên từ độ cao 1 m so với mặt đất, hãy viết phương trình chuyển động của vật
c) Một vận động viên ném lao đã lập kỉ lục với độ xa 90 m. Biết người này ném lao từ độ cao 0,9 m và góc ném là khoảng \(45^\circ \). Hỏi vận tốc đầu của lao khi được ném đi là bao nhiêu?
(Lưu ý: Lấy giá trị \(g = 10\) m/s2 cho gia tốc trọng trường và làm tròn kết quả đến 2 chữ số thập phân)
Một viên bi rơi tự do từ độ cao 19,6 m xuống mặt đất. Độ cao h (mét) so với mặt đất của viên bi trong khi rơi phụ thuộc vào thời gian t (giây) theo công thức: \(h = 19,6 - 4,9{t^2};h,t \ge 0\).
a) Hỏi sau bao nhiêu giây kể từ khi rơi viên bi chạm đất?
b) Tìm tập xác định và tập giá trị của hàm số h.
Bạn Nam đứng dưới chân cầu vượt ba tầng ở nút giao ngã ba Huế, thuộc thành phố Đà Nẵng để ngắm cảnh cầu vượt (H.6.13) Biết rằng trụ tháp cầu có dạng đường parabol, khoảng cách giữa hai chân trụ tháp khoảng 27 m, chiều cao của trụ tháp tính từ điêm trên mặt đất cách chân trụ tháp 2,26 m là 20 m. Hãy giúp bạn Nam ước lượng độ cao của đỉnh trụ tháp cầu (so với mặt đất).

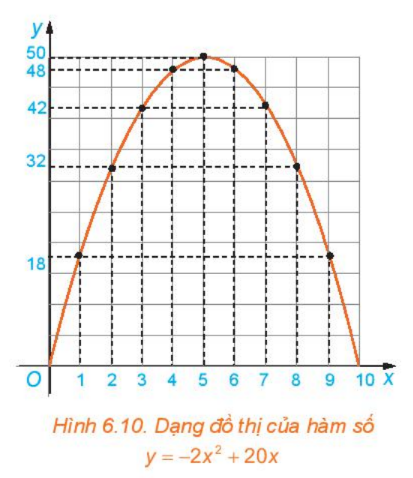
Xét hàm số \(y = S(x) = - 2{x^2} + 20x \) \((0 < x < 10)\).
a) Trên mặt phẳng tọa độ Oxy, biểu diễn tọa độ các điểm trong bảng giá trị của hàm số lập được ở Ví dụ 1. Nối các điểm đã vẽ lại ta được dạng đồ thị hàm số \(y = - 2{x^2} + 20x\)trên khoảng (0; 10) như trong Hình 6.10. Dạng đồ thị \(y = - 2{x^2} + 20x\) có giống với đồ thị của hàm số \(y = - 2{x^2}\) hay không?
b) Quan sát dạng đồ thị của hàm số \(y = - 2{x^2} + 20x\) trong Hình 6.10, tìm tọa độ điểm cao nhất của đồ thị.
c) Thực hiện phép biến đổi \(y = - 2{x^2} + 20x = - 2({x^2} - 10x) = - 2({x^2} - 2.5.x + 25) + 50 = - 2{(x - 5)^2} + 50\). Hãy cho biết giá trị lớn nhất của diện tích mảnh đất được rào chắn. Từ đó suy ra lời giải của bài toán ở phần mở đầu.
Hai bạn An và Bình trao đổi với nhau.
An nói: Tớ đọc ở một tài liệu thấy nói rằng cồng Trường Đại học Bách khoa Hà Nội (H.6.14) có dạng một parabol, khoảng cách giữa hai chân cổng là 8 m và chiều cao của cổng tính từ một điểm trên mặt đất cách chân cổng 0,5 m là 2,93 m. Từ đó tớ tính ra được chiều cao của cổng parabol đó là 12 m
Sau một hồi suy nghĩ, Bình nói: Nếu dữ kiện như bạn nói, thì chiều cao của cổng parabol mà bạn tính ra ở trên là không chính xác.
Dựa vào thông tin mà An đọc được, em hãy tính chiều cao của cổng Trường Đại học Bách khoa Hà Nội để xem kết quả bạn An tính được có chính xác không nhé!

Bác Hùng dùng 40 m lưới thép gai rào thành một mảnh vườn hình chữ nhật để trồng rau.
a) Tính diện tích mảnh vườn hình chữ nhật rào được theo chiều rộng x (mét) của nó.
b) Tìm kích thước của mảnh vườn hình chữ nhật có diện tích lớn nhất mà bác Hùng có thể rào được.
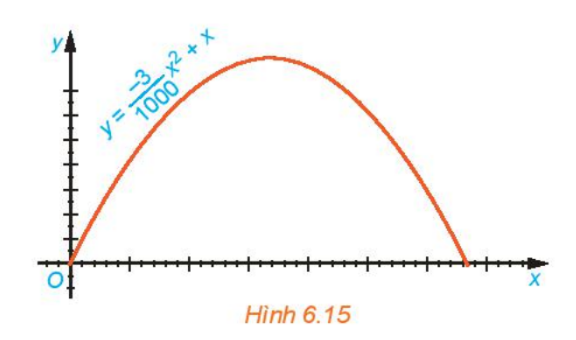
Quỹ đạo của vật được ném lên từ gốc O (được chọn là điểm ném) trong mặt phẳng tọa độ Oxy là một parabol có phương trình \(y = \frac{{ - 3}}{{1000}}{x^2} + x\) , trong đó x (mét) là khoảng cách theo phương ngang trên mặt đất từ vị trí của vật đến gốc O, y (mét) là độ cao của vật so với mặt đất (H.6.15).
a) Tím độ cao cực đại của vật trong quá trình bay.
b) Tính khoảng cách từ điểm chạm mặt đất sau khi bay của vật đến gốc O. Khoảng cách này gọi là tầm xa của quỹ đạo.
Một công ty bắt đầu sản xuất và bán một loại máy tính xách tay từ năm 2018. Số lượng loại máy tính đó bán được trong hai năm liên tiếp 2018 và 2019 lần lượt là 3,2 nghìn và 4 nghìn chiếc. Theo nghiên cứu dự báo thị trường của công ty, trong khoảng 10 năm từ năm 2018, số lượng máy tính loại đó bán được mỗi năm có thể mô tả bởi một hàm số bậc hai.
Giả sử t là thời gian (đơn vị theo năm) tính từ năm 2018. Số lượng loại máy đó bán đượng trong năm 2018 và 2019 lần lượt được biểu diễn bởi các điểm \((0;3,2)\) và \((1;4).\) Giả sử điểm \((0;3,2)\) là đỉnh của đồ thị của hàm số bậc hai này.
a) Lập công thức của hàm số mô tả số lượng máy xách tay bán được qua từng năm.
b) Tính số lượng máy tính xách tay đó bán được trong năm 2024.
c) Đến năm bao nhiêu thì số lượng máy tính xách tay đó bán được trong năm sẽ vượt mức 52 nghìn chiếc?
Bác Hùng dùng 200 m hàng rào dây thép gai để rào miếng đất đủ rộng thành một mảnh vườn hình chữ nhật.
a) Tìm công thức tính diện tích S(x) của mảnh vườn hình chữ nhật rào được theo chiều rộng x (m) của mảnh vườn đó.
b) Tìm kích thước của mảnh vườn hình chữ nhật có diện tích lớn nhất có thể rào được.
Một quả bóng được ném lên trên theo phương thẳng đứng từ mặt đất với vận tốc ban đầu 14,7 m/s. Khi bỏ qua sức cản của không khí, độ cao của quả bóng so với mặt đất (tính bằng mét) có thể mô tả bởi PT:
\(h(t) = - 4,9{t^2} + 14,7t\)
a) Sau khi ném bao nhiêu giây thì quả bóng đạt độ cao lớn nhất?
b) Tìm độ cao lớn nhất của quả bóng.
c) Sau khi ném bao nhiêu giây thì quả bóng rơi chạm đất?
Một hòn đá được ném lên trên theo phương thẳng đứng. Khi bỏ qua sức cản của không khí, chuyển động của hòn đá tuân theo phương trình sau:
\(y = - 4,9{t^2} + mt + n\)
với m, n là các hằng số. Ở đây t = 0 là thời điểm hòn đá được ném lên, y(t) là độ cao của hòn đá tại thời điểm t (giây) sau khi ném và y = 0 ứng với bóng chạm đất.
a) Tìm phương trình chuyển động của hòn đá, biết rằng điểm ném cách mặt đất 1,5 m và thời gian để hòn đá đạt độ cao lớn nhất là 1,2 giây sau khi ném.
b) Tìm độ cao của hòn đá sau 2 giây kể từ khi bắt đầu ném.
c) Sau bao lâu kể từ khi ném, hòn đá rơi xuống mặt đất (Kết quả làm tròn đến chữ số thập phân thứ hai)?
Một rạp chiếu phim có sức chứa 1 000 người. Với giá vé là 40 000 đồng, trung bình sẽ có khoảng 300 người đến rạp xem phim mỗi ngày. Để tăng số lượng vé bán ra, rạp chiếu phim đã kháo sát thị trường và thấy rằng nếu giá vé cứ giảm 10 000 đồng thì sẽ có thêm 100 người đến xem phim mỗi ngày.
a) Tìm công thức của hàm số R(x) mô tả doanh thu từ tiền bán vé mỗi ngày của rạp chiếu phim khi giá vé là x nghìn đồng.
b) Tìm mức giá vé để doanh thu từ tiền bán vé mỗi ngày của rạp là lớn nhất.
Trong Vật lí ta biết rằng, khi một vật được ném xiên với vận tốc ban đầu v0, góc ném hợp với phương ngang Ox một góc \(\alpha \), nếu ta bỏ qua sức cản của không khí và gió, vật chỉ chịu tác dụng của trọng lực với gia tốc trọng trường \(g \approx 9,8\) m/s2, thì độ cao y (so với mặt đất) của vật phụ thuộc vào khoảng cách theo phương ngang x (tính đến mặt đất tại điểm ném) theo một hàm số bậc hai cho bởi công thức
\(y = \frac{{ - g}}{{2v_0^2{{\cos }^2}\alpha }}{x^2} + x\tan \alpha \)
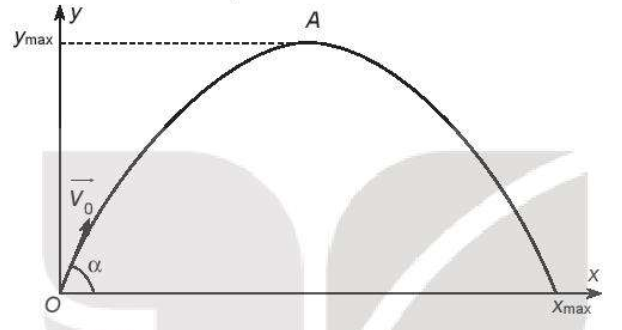
Như vậy quỹ đạo chuyển động của vật là một phần của đường parabol. Hãy xác định:
a) Các hệ số a, b và c của hàm số bậc hai này.
b) Độ cao lớn nhất mà vật có thể đạt được.
c) Giả sử vận tốc ban đầu v0 không đổi. Từ kết quả câu b) hãy xác định góc ném \(\alpha \) để độ cao của vật đạt giá trị lớn nhất.
d) Một quả bóng được đá từ mặt đất lên cao với vận tốc ban đầu v0 = 20 m/s và góc đá so với phương ngang là 450. Khi quả bóng ở độ cao trên 5 m thì khoảng cách theo phương ngang từ vị trí của quả bóng đến vị trí đá bóng nằm trong khoảng nào (làm tròn kết quả đến hàng phần trăm)?
Một công ti kinh doanh máy tính cầm tay thấy rằng khi bán máy ở mức giá x (nghìn đồng) một chiếc thì số lượng máy bán được n cho bởi phương trình n = 1 200 000 – 1 200x.
a) Tìm công thức biểu diễn doanh thu R như là hàm số của đơn giá x. Tìm miền xác định của hàm số R = R(x).
b) Máy tính được bán ở đơn giá nào sẽ cho doanh thu lớn nhất? Tính doanh thu lớn nhất và số máy tính bán được trong trường hợp đó.
c) Với đơn giá nào thì công ti sẽ đạt được doanh thu trên 200 tỉ đồng (làm tròn đến nghìn đồng)?
Một người nông dân thả 1000 con cá giống vào hồ nuôi vừa mới đào. Biết rằng sau mỗi năm thì số lượng cá trong hồ tăng thêm x lần so với lượng cá ban đầu và x không đổi. Bằng cách thay đổi kỹ thuật nuôi và thức ăn cho cá. Hỏi sau hai năm đề số cá trong hồ là 36000 con thì tốc độ tăng số lượng cá trong hồ x là bao nhiêu? Biết tốc độ tăng mỗi năm là không đổi.
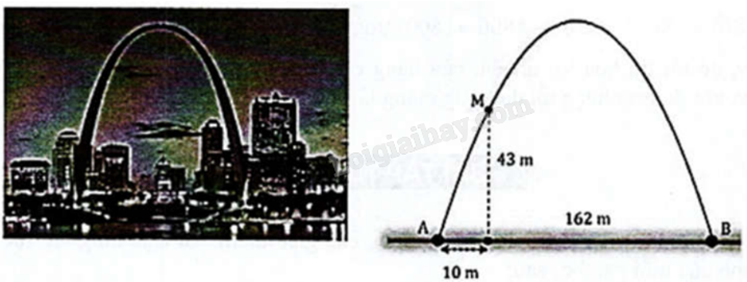
Cổng Arch tại thành phố St Louis của Mỹ có hình dạng một parabol. Biết khoảng cách giữa hai chân cổng là 162 m. Trên thành cổng, tại vị trí có độ cao 43 m so với mặt đất, người ta thả một sợi dây chạm đất và vị trí chạm đất này cách chân cổng (điểm A) một khoảng 10 m. Hãy tính gần đúng độ cao (m) của cổng Arch (làm tròn kết quả đến hàng phần mười).
Một chiếc cổng hình parabol bao gồm một cửa chính hình chữ nhật ở giữa và hai cánh cửa phụ hai bên như hình vẽ.
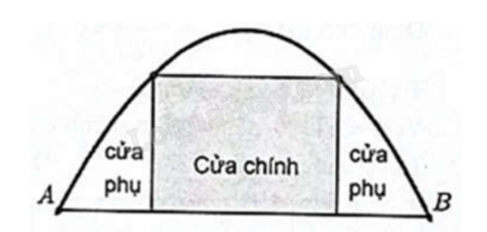
Biết chiều cao cổng parabol là 4 m, cửa chính (ở giữa parabol) cao 3 m và rộng 4 m. Tính khoảng cách giữa hai chân cổng parabol ấy (đoạn AB như hình vẽ).
Người ta thử nghiệm ném một quả bóng trên Mặt Trăng. Nếu quả bóng được ném lên từ độ cao \({h_0}\) (m) so với bề mặt của Mặt Trăng với vận tốc \({v_0}\) (m/s) thì độ cao của quả bóng sau t giây được cho bởi hàm số \(h\left( t \right) = - \frac{1}{2}g{t^2} + {v_0}t + {h_0}\) với \(g = 1,625\) m/s2 là gia tốc trọng trường của Mặt Trăng.
a) Biết độ cao ban đầu của quả bóng vào các thời điểm 8 giây và 12 giây lần lượt là 30 m và 5 m, hãy tìm vận tốc ném; độ cao ban đầu của quả bóng và viết công thức \(h\left( t \right)\).
b) Quả bóng đạt độ cao trên 29 m trong bao nhiêu giây?
Lưu ý: Đáp số làm tròn đến hàng phần trăm.
Một người phát cầu qua lưới từu độ cao \({y_0}\) mét, nghiệm một góc \(\alpha \) so với phương ngang với vận tốc đầu \({v_0}\).
Phương trình chuyển động của quả cầu là:
\(y = \frac{{ - g}}{{2v_0^2{{\cos }^2}\alpha }}{x^2} + \tan \left( \alpha \right)x + {y_0}\) với\(g = 10\) m/s2.
Viết phương trình chuyển động của quả cầu nếu \(\alpha = 45^\circ ,{y_0} = 0,3\) m và \({v_0} = 7,67\) m/s.
b) Để cầu qua được lưới bóng cao 1,5 m thì người phát cầu phải đứng cách lưới bao xa?
Lưu ý: Đáp số làm tròn đến hàng phần trăm.
Một quả bóng chày được đánh đi với vận tốc 35 m/s hợp với phương ngang một góc bằng 45° ở độ cao 1m so với mặt sân phẳng ở chỗ vụt bóng. Bỏ qua sức cản của không khí và lấy g = 9,8 m/s.
a) Biết rằng quỹ đạo chuyển động của quả bóng chày được cho bởi phương trình:
\(y = \frac{{ - g}}{{2{v_o}^2{{\cos }^2}\alpha }}{x^2} + x\tan \alpha + h\)
trong đó x là quãng đường (tính bằng mét) quả bóng bay được theo phương ngang, h là độ cao của quả bóng lúc được đánh đi so với mặt đất, vận tốc ban đầu \({v_o}\) hợp với phương ngang một góc \(\alpha \)
Viết phương trình chuyển động của quả bóng chày.
b) Tính độ cao lớn nhất của quả bóng chày.
c) Tính tầm xa của quả bóng chày, tức là khoảng cách từ mặt đất ở chỗ đánh bóng và nơi quả bóng chạm đất (kết quả làm tròn đến hàng đơn vị).
d) Có một hàng rào cao 4 m cách chỗ đánh bóng 125 m theo hướng đánh bóng. Hỏi quả bóng chày được đánh đi như trên có bị bay qua hàng rào đó hay không?
Một trận bóng đá được tổ chức ở một sân vận động có sức chứa 15000 người. Với giá vé 14\($\) thì trung bình các trận đấu gần đây có 9500 khán giả. Theo một khảo sát thị trường đã chỉ ra rằng cứ giảm 1\($\) mỗi vé thì trung bình số khán giả tăng lên 1000 người. Giá vé bằng bao nhiêu thì thu được nhiều lợi nhuận nhất (đơn vị: $)?
Một cửa hàng nhập vào một loại máy tính xách tay với giá 15 triệu đồng và bán ra với giá 18 triệu đồng. Vói giá bán này, một tháng cửa hàng đó bán được 20 cái máy tính xách tay. Cửa hàng dự định giảm giá bán, ước tính nếu cứ giảm giá bán mỗi máy 500.000 đồng thì số máy tính bán được trong một tháng tăng thêm 5 cái. Xác định giá bán mỗi cái máy tính để lợi nhuận thu được là cao nhất (đơn vị: triệu đồng).
Khi quả bóng được đá lên, nó sẽ đạt độ cao nào đó rồi rơi xuống đất (giống bài toán tầm bay cao, tầm bay xa). Biết quỹ đạo của quả bóng là một parabol trong trục tọa độ Oth với t là thời gian, h là độ cao của quả bóng. Giả thiết rằng quả bóng được đá lên từ độ cao 1,2 m. Sau 1 giây, nó đạt độ cao 8,5 m và 2 giây sau nó ở độ cao 6 m. Hãy tìm hàm số bậc hai biểu thị độ cao h theo thời gian t.
-
A.
\(y = 4,9{t^2} + 12,2t + 1,2\)
-
B.
\(y = - 4,9{t^2} + 12,2t + 1,2\)
-
C.
\(y = 4,9{t^2} + 12,2t - 1,2\)
-
D.
\(y = - 4,9{t^2} - 12,2t + 1,2\)







Danh sách bình luận