Giải toán 7, giải bài tập toán lớp 7 sgk đầy đủ đại số và hình học
Bài 5. Tính chất tia phân giác của một góc
Bài 34 trang 71 SGK Toán 7 tập 2
Cho góc xOy khác góc bẹt
Đề bài
Cho góc \(xOy\) khác góc bẹt. Trên tia \(Ox\) lấy hai điểm \(A\) và \(B\), trên tia \(Oy\) lấy hai điểm \(C\) và \(D\) sao cho \(OA = OC, OB = OD.\) Gọi \(I\) là giao điểm của hai đoạn thẳng \(AD\) và \(BC.\) Chứng minh rằng:
a) \(BC = AD\)
b) \(IA = IC, IB = ID\)
c) Tia \(OI\) là tia phân giác của góc \(xOy\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Chứng minh dựa vào các tam giác bằng nhau.
Lời giải chi tiết
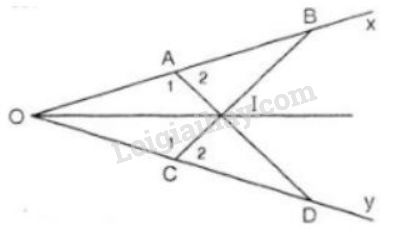
a) Xét \( ∆AOD\) và \(∆COB\) có:
+) \(OA = OC\) (giả thiết)
+) \(OD = OB\) (giả thiết)
+) \(\widehat{xOy}\) là góc chung
Vậy \(∆AOD = ∆COB\) (c.g.c)
\(\Rightarrow\) \(AD = BC\) (hai cạnh tương ứng) (điều phải chứng minh).
b) Vì \(∆AOD = ∆COB\) (câu a) nên \(\widehat{D} = \widehat{B}\) và \(\widehat{C_1} = \widehat{A_1}\) ( 2 góc tương ứng)
Ta có: \(OA + AB = OB\) \(\Rightarrow AB = OB - OA = OD - OC = CD\)
Hay \(AB=CD\)
Ta có: \(\widehat{A_1} + \widehat{A_2} = 180^o\) (\(2\) góc kề bù)
\(\Rightarrow\) \(\widehat{A_2} = 180^o - \widehat{A_1} = 180^o - \widehat{C_1} = \widehat{C_2}\)
Xét \(∆AIB\) và \(∆CID\) ta có:
+) \(AB = CD\) (chứng minh trên)
+) \(\widehat{B} = \widehat{D}\) (chứng minh trên)
+) \(\widehat{A_2} = \widehat{C_2}\) (chứng minh trên)
Vậy \(∆AIB = ∆CID\) (g.c.g)
\(\Rightarrow IC = IA\) và \(ID = IB\) (hai cạnh tương ứng)
c) Xét \(∆OAI\) và \( ∆OCI\) ta có:
+) \(OA = OC\) (giả thiết)
+) \(\widehat{A_1} = \widehat{C_1}\) (chứng minh trên)
+) \(IA = IC\) (chứng minh trên)
Vậy \( ∆OAI = ∆OCI\) (c.g.c)
\(\Rightarrow\widehat{AOI} = \widehat{COI}\) ( 2 góc tương ứng)
\(\Rightarrow\) \(OI\) là phân giác của \(\widehat{xOy}\).
Bình luận
Chia sẻ
- Bài 35 trang 71 SGK Toán 7 tập 2
- Đề kiểm tra 15 phút - Đề số 1 - Bài 5, 6 - Chương 3 – Hình học 7
- Đề kiểm tra 15 phút - Đề số 2 - Bài 5, 6 - Chương 3 – Hình học 7
- Đề kiểm tra 15 phút - Đề số 3 - Bài 5, 6 - Chương 3 – Hình học 7
- Đề kiểm tra 15 phút - Đề số 4 - Bài 5, 6 - Chương 3 – Hình học 7
>> Xem thêm
Tham Gia Group Dành Cho Lớp 7 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
