Bài 3 trang 18 SGK Đại số 10

LG a

\((-2; 3)\backslash (1; 5)\);

Phương pháp giải:

Tập hợp C=A\B gồm các phần tử thuộc A nhưng không thuộc B.

Lời giải chi tiết:

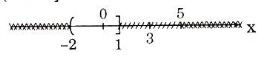
\((-2; 3)\backslash (1; 5) = (-2; 1]\);

Chú ý:

Cách biểu diễn trên trục số:

\((-2; 3)\backslash (1; 5)\) là tập hợp các x chỉ thuộc (-2;3) nhưng không thuộc (1;5). Do đó vẽ hình như sau:

- Vẽ khoảng (-2;3) (các điểm không thuộc khoảng này gạch hết vì x phải thuộc (-2;3))

- Vẽ khoảng (1;5) và gạch toàn bộ khoảng này đi (vì x không thuộc khoảng này)

- Tại điểm -2 là ngoặc tròn, điểm 1 thuộc khoảng (-2;3) và không thuôc khoảng (1;5) nên vẫn lấy được. Do đó để ngoặc vuông.

LG b

\((-2; 3)\backslash [1; 5)\);

Phương pháp giải:

Tập hợp C=A\B gồm các phần tử thuộc A nhưng không thuộc B.

Lời giải chi tiết:

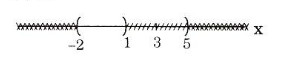
\((-2; 3)\backslash [1; 5) = (-2; 1)\);

Chú ý:

Cách vẽ hình tương tự câu a, chỉ chú ý thêm điểm 1 thuộc nửa khoảng [1;5) nên không thỏa mãn, do đó để ngoặc tròn.

LG c

\(\mathbb R\backslash (2; +∞)\);

Phương pháp giải:

Tập hợp C=A\B gồm các phần tử thuộc A nhưng không thuộc B.

Lời giải chi tiết:

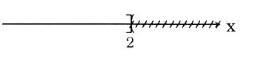
\(\mathbb R\backslash (2; +∞) = (- ∞; 2]\)

Chú ý:

Cách vẽ hình như sau:

- Vẽ trục số và không gạch phần nào hết vì biểu diễn tập số thực R.

- Vẽ khoảng (2; +∞) và gạch toàn bộ khoảng này đi vì x không thuộc khoảng này.

- Điểm 2 lấy được vì \(2\in R\) và 2 không thuộc (2; +∞) nên ở điểm 2 dùng ngoặc vuông.

LG d

\(\mathbb R\backslash (-∞; 3]\).

Phương pháp giải:

Tập hợp C=A\B gồm các phần tử thuộc A nhưng không thuộc B.

Lời giải chi tiết:

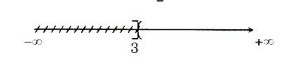
\(\mathbb R\backslash (-∞; 3] = (3; +∞)\).

Chú ý:

Cách vẽ hình:

- Vẽ trục số và không gạch phần nào hết vì biểu diễn tập số thực R.

- Vẽ nửa khoảng (-∞;3] và gạch toàn bộ phần này đi vì x không thuộc phần này.

- Điểm 3 không lấy được vì 3 thuộc (-∞;3] nên không thỏa mãn. Do đó ở điểm 3 dùng ngoặc tròn.

Loigiaihay.com