 Giải toán 10, giải bài tập toán lớp 10 đầy đủ đại số và hình học
Giải toán 10, giải bài tập toán lớp 10 đầy đủ đại số và hình học
 Bài 4. Bất phương trình bậc nhất hai ẩn
Bài 4. Bất phương trình bậc nhất hai ẩn
Bài 2 trang 99 SGK Đại số 10
Biểu diễn hình học tập nghiệm của các hệ bất phương trình hai ẩn sau...
Video hướng dẫn giải
Biểu diễn hình học tập nghiệm của các hệ bất phương trình hai ẩn sau.
LG a
\(\left\{\begin{matrix} x-2y<0\\ x+3y>-2 \\ y-x<3; \end{matrix}\right.\)
Phương pháp giải:
Ta biểu diễn hình học tập nghiệm của từng bất phương trình của hệ, nghiệm chung của chúng chính là nghiệm của hệ bất phương trình đã cho.
Quy tắc thực hành biểu diễn hình học tập nghiệm (hay biểu diễn miền nghiệm) của bất phương trình \(ax + by \le c\left( {ax + by \ge c} \right)\)
Bước 1: Trên mặt phẳng tọa độ Oxy, vẽ đường thẳng (d): ax + by = c.
Bước 2: Lấy một điểm \(M\left( {{x_0};{y_0}} \right)\) không thuộc (d) (ta thường lấy gốc tọa độ).
Bước 3: Tính \(a{x_0} + b{y_0}\) và so sánh \(a{x_0} + b{y_0}\) với c.
Bước 4: Kết luận:
+) Nếu \(a{x_0} + b{y_0} < c\) thì nửa mặt phẳng bờ (d) chứa M là miền nghiệm của \(a{x_0} + b{y_0} \le c\).
+) Nếu \(a{x_0} + b{y_0} > c\) thì nửa mặt phẳng bờ (d) không chứa M là miền nghiệm của \(a{x_0} + b{y_0} \ge c\).
Lời giải chi tiết:
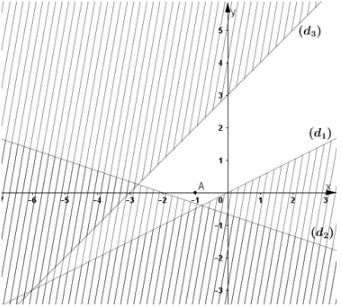
Ta vẽ các đường thẳng x – 2y = 0 (\(d_1\)) ; x + 3y = –2 (\(d_2\)) ; –x + y = 3 (\(d_3\)).
Điểm A(–1; 0) có tọa độ thỏa mãn tất cả các bất phương trình trong hệ nên ta gạch đi các nửa mặt phẳng bờ (\(d_1\)); (\(d_2\)); (\(d_3\)) không chứa điểm A.
Miền nghiệm của hệ bất phương trình là miền không bị gạch sọc ở hình bên dưới (không kể các bờ).
LG b
\(\left\{\begin{matrix} \dfrac{x}{3}+\dfrac{y}{2}-1<0\\ x+\dfrac{1}{2}-\dfrac{3y}{2}\leq 2 \\ x\geq 0. \end{matrix}\right.\)
Lời giải chi tiết:
Ta có:
\(\begin{array}{l}
\left\{ \begin{array}{l}
\dfrac{x}{3} + \dfrac{y}{2} - 1 < 0\\
x + \dfrac{1}{2} - \dfrac{{3y}}{2} \le 2\\
x \ge 0
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
\dfrac{{2x + 3y - 6}}{6} < 0\\
\dfrac{{2x + 1 - 3y - 4}}{2} \le 0\\
x \ge 0
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
2x + 3y - 6 < 0\\
2x - 3y - 3 \le 0\\
x \ge 0
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
2x + 3y < 6\\
2x - 3y \le 3\\
x \ge 0
\end{array} \right.
\end{array}\)
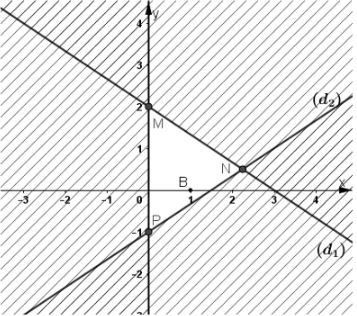
Ta vẽ các đường thẳng 2x + 3y = 6 (\(d_1\)); 2x – 3y = 3 (\(d_2\)); x = 0 (trục tung).
Điểm B(1; 0) có tọa độ thỏa mãn tất cả các bất phương trình trong hệ nên ta gạch đi các nửa mặt phẳng bờ (\(d_1\)); (\(d_2\)) và trục tung không chứa điểm B.
Miền không bị gạch chéo (tam giác MNP, kể cả cạnh MP và NP, không kể cạnh MN) là miền nghiệm của hệ bất phương trình đã cho.
Loigiaihay.com












Danh sách bình luận