Bài 1 trang 88 SGK Hình học 10
Xác đinh độ dài các trục, tọa độ tiêu điểm , tọa độ các đỉnh và vẽ các elip có phương trình sau:
Video hướng dẫn giải
Xác định độ dài các trục, tọa độ tiêu điểm, tọa độ các đỉnh và vẽ các elip có phương trình sau:
LG a
\(\frac{x^{2}}{25} + \frac{y^{2}}{9}= 1.\)
Phương pháp giải:
Cho phương trình ellip: \(\left( E \right):\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{b^2} = 1.\)
Khi đó:
+) Độ dài trục lớn là: \(2a\) và độ dài trục nhỏ là \(2b.\)
+) Tọa độ các đỉnh là: \({A_1}\left( { - a;\;0} \right),\;{A_2}\left( {a;\;0} \right),\;{B_1}\left( { - b;\;0} \right),\)\(\;{B_2}\left( {b;\;0} \right).\)
+) Tọa độ tiêu điểm: \({F_1}\left( { - c;\;0} \right),\;{F_2}\left( {c;\;0} \right)\) với \(c^2=a^2-b^2.\)
Lời giải chi tiết:
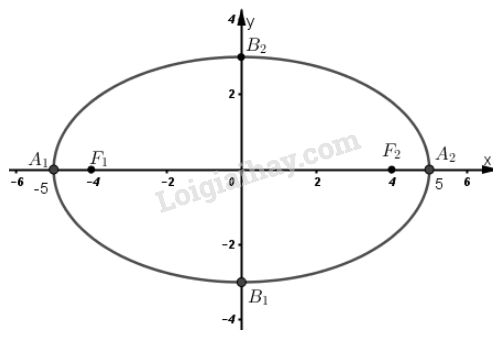
Ta có: \(a^2= 25 \Rightarrow a = 5\) độ dài trục lớn \(2a = 10\)
\( b^2= 9 \Rightarrow b = 3\) độ dài trục nhỏ \(2b = 6\)
\(c^2= a^2– b^2= 25 - 9 = 16 \Rightarrow c = 4\)
Vậy hai tiêu điểm là : \(F_1(-4 ; 0)\) và \(F_2(4 ; 0)\)
Tọa độ các đỉnh \(A_1(-5; 0), A_2(5; 0), B_1(0; -3), B_2(0; 3)\).
LG b
\(4x^2+ 9y^2= 1.\)
Lời giải chi tiết:
\(4x^2+ 9y^2= 1\Leftrightarrow \dfrac{x^{2}}{\dfrac{1}{4}} + \dfrac{y^{2}}{\dfrac{1}{9}} = 1\)
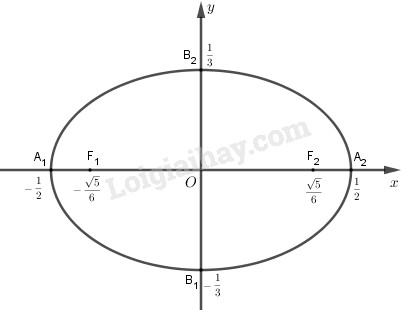
\(a^2 =\dfrac{1}{4}\Rightarrow a = \dfrac{1}{2}\) \(\Rightarrow\) độ dài trục lớn \(2a = 1\)
\(b^2= \dfrac{1}{9}\Rightarrow b = \dfrac{1}{3}\) \(\Rightarrow\) độ dài trục nhỏ \(2b = \dfrac{2}{3}\)
\(c^2= a^2– b^2= \dfrac{1}{4}- \dfrac{1}{9} = \dfrac{5}{36}\) \(\Rightarrow c = \dfrac{\sqrt{5}}{6}\)
\(F_1(-\dfrac{\sqrt{5}}{6} ; 0)\) và \(F_2(\dfrac{\sqrt{5}}{6} ; 0)\)
\(A_1(-\dfrac{1}{2}; 0), A_2(\dfrac{1}{2}; 0)\), \(B_1(0; -\dfrac{1}{3} ), B_2(0; \dfrac{1}{3} )\).
LG c
\(4x^2+ 9y^2= 36.\)
Lời giải chi tiết:
Chia \(2\) vế của phương trình cho \(36\) ta được :
\(\dfrac{x^{2}}{9}+ \dfrac{y^{2}}{4}= 1\)
Ta có:
\(\begin{array}{l}
{a^2} = 9 \Rightarrow a = 3\\
{b^2} = 4 \Rightarrow b = 2\\
{c^2} = {a^2} - {b^2} = 5 \Rightarrow c = \sqrt 5
\end{array}\)
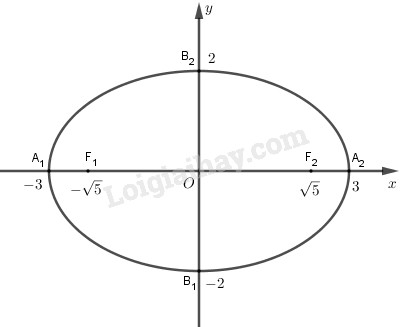
+) Độ dài trục lớn \(2a = 6\)
+) Độ dài trục nhỏ \( 2b = 4\).
+) Tiêu điểm \(F_1(-\sqrt5 ; 0)\) và \(F_2(\sqrt5 ; 0)\)
+) Các đỉnh \(A_1(-3; 0), A_2(3; 0), B_1(0; -2), B_2(0; 2)\).
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 2 trang 88 SGK Hình học 10
- Bài 3 trang 88 SGK Hình học 10
- Bài 4 trang 88 SGK Hình học 10
- Giải bài 5 trang 88 SGK Hình học 10
- Câu hỏi 4 trang 87 SGK Hình học 10
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
