Xác suất có điều kiện là gì? Định nghĩa, công thức, cách tính - Toán 12

Cho hai biến cố A và B. Xác suất của biến cố A khi biến cố B đã xảy ra được gọi là xác suất của A với điều kiện B và kí hiệu là P(A|B).

Cho hai biến cố A và B bất kì, với P(B) > 0. Khi đó:

\(P(A|B) = \frac{{P(A \cap B)}}{{P(B)}}\)

Với hai biến cố A và B bất kì, ta có:

\(P(AB) = P(B).P(A|B) = P(A).P(B|A)\)

1) Một hộp có 5 viên bi cùng kích thước và khối lượng, trong đó có 3 viên bi màu đỏ và 2 viên bi màu xanh. Lấy ngẫu nhiên lần lượt 2 viên bi và không hoàn lại. Tính xác suất để lấy được viên bi thứ hai có màu xanh, biết rằng viên bi thứ nhất có màu đỏ.

Giải:

Gọi A là biến cố "Lấy được viên bi thứ hai có màu xanh";

B là biến cố "Lấy được viên bi thứ nhất có màu đỏ".

Khi đột xác suất để lấy được viên bi thứ hai có màu xanh, biết rằng viên bi thứ nhất có màu đỏ chính là xác suất của A với điều kiện B.

Vì một viên bi đỏ đã được lấy ra ở lần thứ nhất nên trong hợp còn lại 4 viên bi, trong đó có 2 viên bi xanh.

Từ đó ta có: \(P(A\mid B) = \frac{2}{4} = 0,5\).

Vậy xác suất để lấy được viên bi thứ hai có màu xanh, biết rằng viên bi thứ nhất có màu đỏ là 0,5.

2) Trong cuộc khảo sát trên một nhóm học sinh gồm các bạn thích trà sữa hoặc kem, người ta có được kết quả sau: Có 56% số học sinh thích kem, 68% số học sinh thích trà sữa, 24% số học sinh thích cả trà sữa và kem. Chọn ngẫu nhiên một bạn học sinh trong nhóm được khảo sát này. Tính xác suất để chọn được học sinh thích kem, biết rằng học sinh đó thích trà sữa.

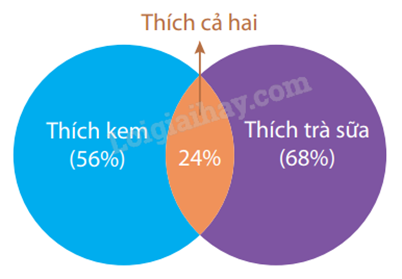
Giải:

Gọi: A là biến cố "Chọn được học sinh thích kem";

B là biến cố "Chọn được học sinh thích trà sữa".

Khi đó xác suất để chọn được học sinh thích kem, biết rằng học sinh đó thích trà sữa chính là xác suất của A với điều kiện B.

Vì có 68% số học sinh thích trà sữa trong nhóm khảo sát nên P(B) = 68% = 0,68.

Ta có AB là biến cố "Chọn được học sinh thích cả trà sữa và kem".

Vì có 24% số học sinh thích cả trà sữa và kem nên P(AB) = 24% = 0,24.

Vì thế ta có: \(P(A\mid B) = \frac{{P(AB)}}{{P(B)}} = \frac{{0,24}}{{0,68}} = 0,35\).

Vậy xác suất để chọn được học sinh thích kem, biết rằng học sinh đó thích trà sữa là 0,35.

3) Trong kỳ kiểm tra môn Toán của một trường trung học phổ thông có 200 học sinh tham gia, trong đó có 95 học sinh nam và 105 học sinh nữ. Khi công bố kết quả của kỳ kiểm tra đó, có 50 học sinh đạt điểm giỏi, trong đó có 24 học sinh nam và 26 học sinh nữ. Chọn ra ngẫu nhiên một học sinh trong số 200 học sinh đó. Tính xác suất để học sinh được chọn ra đạt điểm giỏi, biết rằng học sinh đó là nữ (làm tròn kết quả đến hàng phần trăm).

Giải:

Xét hai biến cố sau:

A: "Học sinh được chọn ra đạt điểm giỏi".

B: "Học sinh được chọn ra là học sinh nữ".

Khi đó, xác suất để học sinh được chọn ra đạt điểm giỏi, biết rằng học sinh đó là nữ, chính là xác suất của A với điều kiện B.

Do có 26 học sinh nữ đạt điểm giỏi nên \(P(A \cap B) = \frac{{26}}{{200}} = 0,13\).

Do có 105 học sinh nữ nên \(P(B) = \frac{{105}}{{200}} = 0,525\). Vì thế, ta có:

\(P(A|B) = \frac{{P(AB)}}{{P(B)}} = \frac{{0,13}}{{0,525}} \approx 0,25\).

Vì thế, ta có:

Vậy xác suất để học sinh được chọn ra đạt điểm giỏi, biết rằng học sinh đó là nữ, là 0,25.